純比例導引律解析解與三維碰撞角約束制導

廖選平，黎克波，劉遠賀，陳 磊

(1.國防科技大學 空天科學學院，長沙 410073; 2.中國人民解放軍軍事科學院 國防科技創新研究院，北京 100071)

碰撞角約束(impact angle constraints,IAC)可以有效提高導彈對目標的打擊效果，對防御武器也具有很好的突防效果(例如垂直打擊)，是當前導彈制導領域研究的重點問題之一[1]。

碰撞角約束制導律(impact angle constrained guidance law,IACG)通常由比例導引律(proportional navigation,PN)加上碰撞角偏差控制項組成，目的是使碰撞角偏差在終點時刻收斂至極小值[2]。最優控制理論是設計IACG的主要方法之一。Zarchan[3]基于施瓦茨不等式，推導了一種碰撞角約束最優制導律，稱為“彈道成型制導律”(trajectory shaping guidance law,TSG)。陳克俊等[4]基于線性二次型最優控制理論，推導了一種落角約束最優制導律。然而，上述2種制導律都不能使導彈指令過載在攔截時刻收斂至0。最近， He等[5]基于最優誤差動力學理論，提出了可使導彈指令過載在命中時刻收斂至0的一種碰撞角約束最優制導律(impact angle constrained optimal guidance law，IACOG)，可增強導彈在末段對干擾的魯棒性，提高了制導律的實用性。

滑模控制對系統的干擾和不確定性具有較強的魯棒性，很多學者基于高階滑模控制理論，提出了多種碰撞角約束滑模制導律(impact angle constrained sliding mode guidance law，IACSMG)[6-8]。近期，同時滿足飛行時間約束和碰撞角約束的制導律設計逐漸成為導彈制導領域研究的熱點問題[9-10]。

然而目前已有的各種IACG仍然存在一些缺陷，例如：IACOG的推導過程通常基于線性化假設，并且引入了剩余飛行時間估計[5]，導致制導律性能并非理論上的全局有效；IACSMG的指令加速度形式較為復雜，且引入的測量量較多，使其實用性受到限制[6-10]。

實際上，僅使用經典純比例導引律(PPN)就可以實現對固定目標的碰撞角約束制導。Lu等[11]首先基于PPN表達式的直接積分，提出了變比例導引系數的三維碰撞角約束PPN制導策略，可適用于變速飛行器。胡正東等[12]在此基礎上進一步推導了以高度為特征變量的垂直打擊三維自適應PPN。然而，上述2種方法未深入探究PPN打擊固定目標的解析解,可能導致某些應用上的不便。

本文基于PPN攔截固定目標的解析解，重新設計三維空間中的碰撞角約束制導律。PPN的指令加速度垂直于導彈速度矢量[13]，在攔截固定目標時，導彈速度矢量與彈目相對速度矢量重合。根據PN的統一方法[14]，可以認為此時PPN與理想比例導引律(ideal proportional navigation law，IPN)[15]是等價的。IPN在攔截非機動目標時有解析解，因而可以基于此直接得到PPN攔截固定目標的解析解。文獻[16]基于以上方法，設計了基于PPN的二維碰撞角約束制導律(2D-PPNIACG)。

本文在文獻[16]的基礎上，首先深入分析了2D-PPNIACG對固定目標的攔截制導性能，包括最大過載、能量消耗和捕獲區域。然后基于對空間幾何關系的深入分析和合理近似，提出了在俯沖平面和轉彎平面同時實現碰撞角約束的基于PPN的三維碰撞角約束制導律(3D-PPNIACG)。最后通過數值仿真算例，驗證了所提出制導律的有效性與可靠性。

1 二維PPNIACG回顧

二維攔截幾何如圖1所示。oI-xIyI為參考慣性系，q為視線角；er為視線方向單位矢量，由OIXI軸逆時針旋轉角度q得到；eθ為垂直于視線方向的單位矢量，由er逆時針旋轉90°獲得；vm為導彈(用下標m來表示)速度矢量，vm為導彈的速度大小；φm為導彈速度傾角，以逆時針方向為正；am為導彈加速度矢量，am為導彈加速度大小；θm=φm-q為導彈前置角。

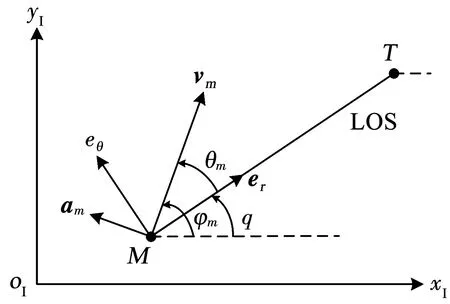
圖1 二維攔截幾何

在動坐標系(er,eθ)內構建的二維相對運動方程為

(1)

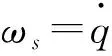
(2)

PN的統一結構為[14]

aPN=NL×ωs

(3)

式中L為參考速度矢量。對于PPN，有L=-vm。

當目標固定時，有

vt=0,at=0

(4)

因而有

(5)

因此也可將PPN的指令加速度寫為

(6)

將式(4)和式(6)代入式(1)，相對運動方程變為

(7)

由式(7)的第2式可推導出：

(8)

再將式(8)代入式(7)的第1式，可推導出：

(9)

并且可進一步推導出[16]：

(10)

由式(10)可知，PPN在攔截固定目標時，導彈前置角會隨彈目相對距離的減小而逐漸收斂至0，即導彈速度方向將逐漸收斂于視線方向。

對PPN還可進一步推導出[16]：

θm-θm0=(N-1)(q-q0)

(11)

于是可得

(12)

由于式(10)已經表明了θm將隨r減小而逐漸收斂至0，即θmf=0，因此由式(12)可知

(13)

由式(13)可知，對攔截固定目標的情況，PPN的攔截碰撞角φmf由初始視線角q0、導彈初始前置角θm0和比例導引系數N所共同決定。

文獻[16]所提出的2D-PPNIACG為：先選擇合適的常值N，再構造合適的彈目初始幾何關系，使導彈沿當前狀態無控飛行，當彈目相對運動狀態滿足式(13)時即自動轉入PPN制導，然后可獲得想要的攔截碰撞角φmf。并且，在使用PPN進行攔截碰撞角約束制導的過程中，可以根據實時的q(t)、θm(t)情況，計算實時所需的比例導引系數，即

(14)

式(14)將導致比例導引系數N的時變性。對其取變分可得

(15)

由于在導彈飛行過程中，在控制穩定的情況下，實際前置角、視線角和理論制導彈道之間的誤差是很小的，因而所引起的N的變化也是很小的。根據式(15)，當接近攔截終點時刻時，q趨近于qf，此時可將N固定，以避免奇異現象的發生。

2 攔截性能分析

導彈在打擊目標的飛行過程中，所關心的問題主要有：最大過載、能量消耗與捕獲區域。

2.1 最大過載

最大過載即為導彈在攔截飛行過程中可能出現的最大指令加速度。由式(6)可得

(16)

意味著PPN指令加速度也會隨著彈目距離的減小而逐漸降低至0，則其最大過載出現在初始時刻，即

(17)

2.2 能量消耗

在制導律分析中，通常可將指令加速度的積分(即導彈攔截所消耗的速度增量)作為導彈的能量消耗。

由式(16)可進一步計算出整個攔截過程中PPN所需的速度增量為

(18)

可近似認為此即為導彈飛行的能量消耗。

2.3 捕獲區域

當導彈從某個特定的相對運動狀態區域內出發時，如果可確保對目標的攔截捕獲，則此初始相對運動狀態區域即為捕獲區域。

要使導彈實現對目標的打擊，需要使彈目相對距離降低至0，且此時保證導彈朝著目標飛行，即彈目接近速度小于0，即

(19)

此即為捕獲的定義[14]。將式(7)的自變量從時間t變成視線角q，即

(20)

式中：x為任意因變量，上標“′”代表對q求導。則式(7)可以改寫為

(21)

再考慮：

(22)

可將式(21)無量綱化，即

(23)

式中，ψ0=cos-1(vθ0/v0)=cos-1(vθ0/vm)為初始相對速度與初始視線的偏離程度，如圖2所示。

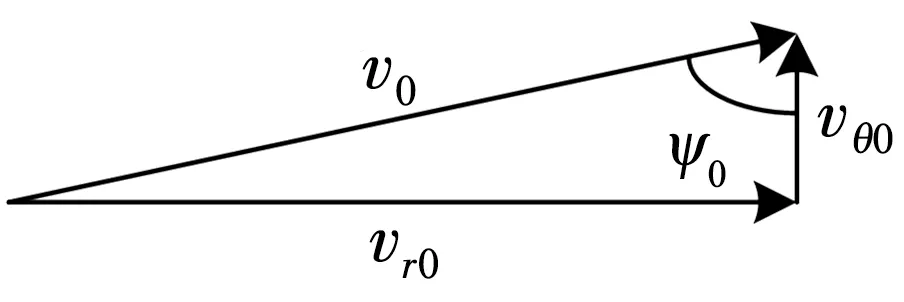
圖2 初始相對速度相對于初始視線的偏離程度

求解式(23)可得

(24)

式中，需滿足k=N-1>0。由式(19)、(20)和式(22)，捕獲的定義可以轉換為：

(25)

(26)

將其代入式(24)的第1式，有

(27)

可知，只要滿足N>1即k>0，則對固定目標，無論導彈從任何條件下出發，在不考慮最大過載約束的情況下，PPN都能實現對目標的攔截。

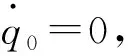
如果考慮導彈過載限制，由式(2)的第2式和式(17)，若需使其小于某最大值α，需使：

(28)

式中，需滿足N>2。式(28)即為以θm0表示的PPN對固定目標的捕獲區域。可知，當導彈受到過載限制時，前置角不能過大，否則不能實現對固定目標的攔截。

3 基于PPN的攔截碰撞角約束制導策略

三維制導律的經典設計方法是將三維相對運動在兩個相互垂直的平面內進行解耦，分別設計二維制導律，然后再進行三維空間中的綜合。

三維攔截幾何如圖3所示。

圖3 基于經典垂直分解的三維攔截幾何

圖4中，oI-xIyIzI為參考慣性系，oI-xsyszs為視線坐標系，oI-xvyvzv為導彈速度坐標系，qε為視線俯仰角、qβ為視線方位角，φ′m為俯仰前置角，ψ′m為偏航前置角，xvoIyv平面為俯沖平面，xvoIzv平面為轉彎平面。

導彈的控制力主要是氣動升力和側向力，其方向沿速度系的yv和zv方向。因此，可以認為導彈制導律的指令加速度為

am=amyvyv+amzvzv

(29)

在小角假設下，對導彈在三維空間中的碰撞角約束制導，可將其解耦為俯沖平面內的落角約束制導和轉彎平面內的碰撞角約束制導。

3.1 俯沖平面落角約束制導

假設攔截過程中ψ′m總為較小值，可以近似認為俯沖平面xvoIyv和視線鉛垂面xsoIys。此時俯沖平面內彈目空間幾何的近似關系如圖4所示。

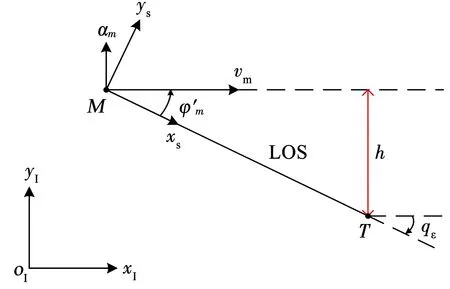
圖4 俯沖平面內的2D-PPNIACG

可使

(30)

并使用文獻[16]中的2D-PPNIACG制導策略。

先使導彈在一定高度h下保持平飛，針對預設的比例導引系數Ny，有

(31)

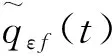
(32)

時，采用式(30)進行制導控制。式中，δε為設定的門限值。

為增強制導律的魯棒性，可采用式(14)進行比例導引系數的實時更新，即

(33)

(34)

如此即可實現落角約束制導，即

(35)

式中tf為攔截終點時刻。

注意，在使用PPNIACG進行落角約束制導時，可使導彈初始時刻距離目標較遠，使|qε0|較小。由圖4可知，在導彈平飛過程中，|qε|不斷增大，相應φ′m也在不斷增大。假設可以使導彈較遠處向目標平飛，設qε0=-20°，并且限制在qε=-60°之前轉入PPN。為保證制導控制系統的魯棒性，通常取N=3～5時。此時根據式(31)，可得落角可能的范圍是-25°～-90°，可以滿足一般落角約束控制的要求。

3.2 轉彎平面碰撞角約束制導

對轉彎平面，可近似認為qε和φ′m均為較小值，則可認為xsoIx″平面與xIoIx′平面重合。

如圖5所示，不失一般性，假設初始時刻導彈向目標飛行，即

qβ(t0)=0,ψ′m(t0)=0

(36)

此時若直接使用PPN進行制導控制，則導彈將直接飛向目標，將有qβf(tf)=qβf。

圖5 轉彎平面內的2D-PPNIACG

因此可以首先采用最大過載或偏置比例導引(BPPN)，使導彈產生一個較大的零控脫靶量D(類比于圖4中的飛行高度h)，以獲得產生碰撞角約束的可能性。

當導彈速度方向產生一定偏移，并因此產生一定的零控脫靶量D后，可使

(37)

針對預設的比例導引系數Nz，有

(38)

(39)

時，采用式(37)進行制導控制。式中，δβ為設定的門限值。

為增強制導律的魯棒性，可采用式(14)進行比例導引系數的實時更新，即

(40)

(41)

如此即可實現落角約束制導，即

(42)

式中tf為攔截終點時刻。

4 仿真算例

文獻[16]通過與彈道成型制導律(TSG)[3]和一種最優碰撞角約束制導律(IACOG)[5]的仿真對比分析，已經驗證了2D-PPNIACG的有效性和優越性。

本文通過數值仿真算例，驗證3D-PPNIACG的有效性和可靠性。導彈與目標的初始運動狀態見表1。

表1 初始彈目相對運動狀態

由表1可知，初始俯仰前置角φ′m0=20°，初始偏航前置角ψ′m0=0°。初始時刻導彈朝目標平飛，如圖6所示。

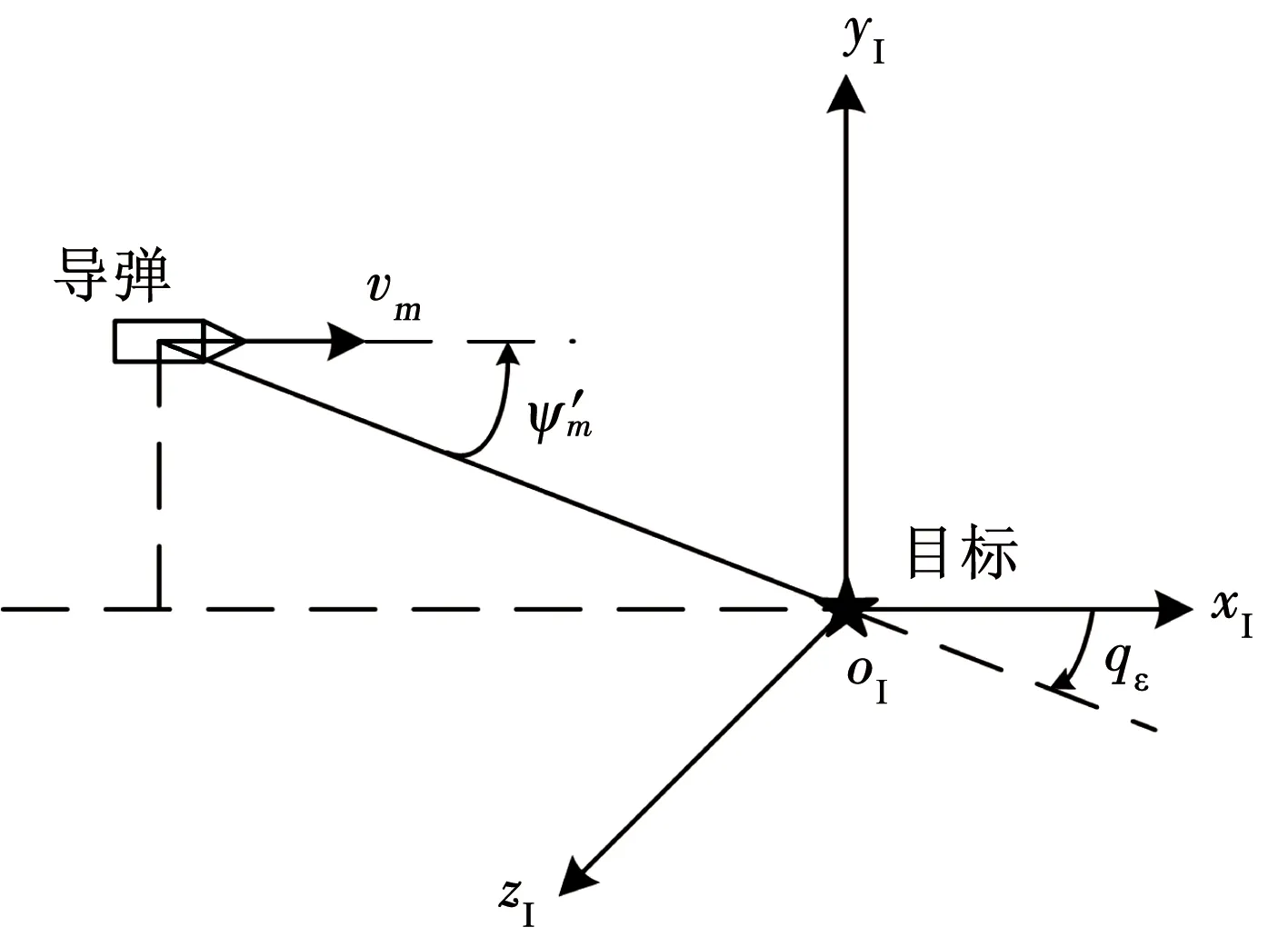
圖6 初始時刻攔截幾何

采用基于PPN的攔截碰撞角約束制導策略所給出的3D-PPNIACG對導彈進行制導控制。設俯沖平面內的落角約束為qεf=-90°，轉彎平面內的碰撞角約束為qβf=60°。

對俯沖平面，設Ny=3，δε=5°；對轉彎平面，同樣設Nz=3，δβ=5°。

4.1 理想情況仿真結果

首先不考慮導彈測量誤差與執行機構響應延遲等干擾和影響因素。仿真結果如圖7所示。

由圖7(a)～圖7(c)可知，本文所設計的3D-PPNIACG可以實現俯沖平面的落角約束和轉彎平面內的碰撞角約束，導彈的飛行彈道較為平滑。

由圖7(d)、圖7(e)可知，在導彈的俯沖和轉彎平面內，前置角φ′m、ψ′m收斂至0，而視線角均收斂到了所設計終端約束值qεf=-90°和qβf=60°極小的領域內。由圖7(f)可知，在導彈飛行過程中，兩個方向視線轉率的絕對值總保持在0.1 rad/s內，并且在攔截末段視線轉率逐漸降低至0附近。由圖7(g)可知，在俯沖平面內，導彈在y方向的加速度先為0，當彈目相對運動狀態符合PPNIACG的攔截幾何關系時，轉入PPNIACG制導。此時導彈的加速度先達到某個最大值，然后逐漸降低至0。在轉彎平面內，導彈先采用BPPN進行轉彎；然后轉為平飛；當彈目相對運動狀態滿足PPNIACG的攔截幾何時，轉入PPNIACG制導。此時導彈的加速度同樣先達到某個最大值，然后逐漸降低至0。在制導過程中，導彈的最大過載都沒有超過其飽和過載。

4.2 考慮現實影響因素的仿真結果

在理想情況仿真條件的基礎上，考慮視線轉率測量誤差為1×10-4rad/s，將彈體執行機構響應延遲近似為一階慣性環節，時間常數τ=0.2 s，設導彈y方向和z方向的飽和過載均為amax=100 m/s2，并且考慮當彈目相對距離小于50 m時，認為導彈導引頭進入盲區，使制導指令切換為0，仿真結果如圖8所示。

圖8 現實干擾因素影響下的仿真結果

由圖8(a)～8(c)可知，在考慮現實影響因素的情況下，3D-PPNIACG也可以實現俯沖平面的落角約束和轉彎平面內的碰撞角約束。

由圖8(d)可知，在存在測量誤差、執行機構響應延遲、導引頭盲區等現實干擾因素的情況下，視線俯仰角收斂到了所設計終端約束值qεf=-90°附近，視線方位角除最終時刻出現跳躍外，均位于qβf=60°附近。實際上，qβ在終端時刻的跳躍主要是由于相對距離進入導引頭盲區后指令加速度切換為0導致的。

由圖8(e)可知，在導彈的俯沖和轉彎平面內，前置角φ′m、ψ′m收斂至0。

由圖8(f)可知，在導彈飛行過程中，兩個方向視線轉率真實值和濾波值的絕對值總保持在0.1 rad/s內，并且在攔截末段視線轉率逐漸降低至0附近。由于導引頭盲區的影響，視線轉率在終點時刻出現跳躍。

由圖8(g)可知，導彈在y方向的加速度先為0，當彈目相對運動狀態符合PPNIACG的攔截幾何關系時，轉入PPNIACG制導。此時導彈加速度指令先達到某個最大值，然后逐漸降低至0。在轉彎平面內，導彈先采用BPPN進行轉彎；然后轉為平飛；當彈目相對運動狀態滿足PPNIACG的攔截幾何時，轉入PPNIACG制導。此時導彈的加速度指令同樣先達到某個最大值，然后逐漸降低至0。受一階慣性環節的影響，導彈實際加速度稍微之后于指令加速度，其從0階躍到最大值的過程趨于平緩。在實際的制導律應用過程中，導彈的姿控系統本身具有時滯性，同時可以使用濾波器對攻角指令進行平滑處理，并且對攻角指令的最大值施加限制，因而對于在轉入PPN制導時，所產生的突然的加速度指令階躍并不會對導彈的控制穩定產生較大影響。值得注意的是，可以根據式(17)對導彈可能產生的最大過載進行設計和估計，從而避免過載飽和現象的出現。在本仿真算例中，導彈的最大過載就沒有超過其飽和過載。

仿真所得導彈脫靶量為0.005 6 m，俯沖平面內的落角偏差為-1.570 8°，轉彎平面內的碰撞角偏差在終端跳躍前為1.047 2°。可知本文所提出的3D-PPNIACG在考慮現實干擾因素的影響下，對固定目標的碰撞角約束打擊仍然具有較好的攔截制導性能。

5 結 論

1)本文基于純比例導引律(PPN)對固定目標的解析解，深入分析了基于純比例導引的二維碰撞角約束制導律(2D-PPNIACG)的攔截制導性能，包括最大過載、能量消耗與捕獲區域。

2)進一步基于小角假設和三維攔截制導的垂直分解方法，提出了基于純比例導引的三維碰撞角約束制導律(3D-PPNIACG)，對固定目標可同時實現俯沖平面內的落角約束打擊和轉彎平面內的碰撞角約束打擊。

3)通過對數值仿真算例的分析可知，無論在理想情況下，還是在考慮測量誤差、執行機構響應延遲、導引頭盲區等現實干擾因素的情況下，3D-PPNIACG對固定目標都具有良好的攔截制導性能。

4)本文所提出的3D-PPNIACG基于經典的PPN制導律，不需要估計剩余飛行時間等狀態變量，其結構簡單、易于實現、魯棒性好，因而具有良好的應用前景。