熵修正的混合人工蜂群-蝙蝠算法人群疏散模型

郁彤彤，王 堅，陳曉薇

(同濟大學 CIMS研究中心，上海 201804)

發生突發事件時，能否高效安全疏散直接關系到公眾生命財產安全，是對安保能力的巨大挑戰。因此，研究人群的安全有序疏散，建立合理安全快速的疏散模型并利用計算機進行模擬仿真，是國內外一直以來的重要研究課題。目前人群疏散模型主要分為微觀模型[1-2]、介觀模型[3]和宏觀模型[4]。由于微觀疏散模型以個體建模為出發點，能夠對復雜動態疏散環境中個體間的微觀相互作用進行描述，在目前研究中更為廣泛。

相比社會力、元胞自動機等微觀模型，群智能疏散模型由于模型簡單、運算速度快、且能夠較真實的模擬行人運動等優點，為越來越多學者關注。Aymaz等[5]針對火災疏散場景，采用PSO算法對疏散路徑進行了優化；王超等[6]基于靜態地面場模型和粒子群優化模型，構建了地面場PSO(FF-PSO)人群疏散模型，可用于高密度人群的擁擠管理和快速疏散問題；Yamamoto等[7]使用蟻群算法對東京市中心的疏散路線安全性進行了量化評估；Yan等[8]構建了一種基于ACO算法的實時消防疏散系統(RFES-ACO)，公眾可以使用移動Web3D設備順暢地實時體驗火災疏散演練。

然而這些模型大多只考慮了粒子群算法、蟻群算法等單一的經典算法，不足以描述復雜的群體疏散行為，且應用新型群智能算法進行人群疏散建模的研究較少。由于生物群體動力學與人群疏散動力學具有一定的相似性[9]，許多新型群智能算法十分適合描述疏散中的不同場景。如，螢火蟲算法適合描述疏散中的從眾心理與行為；人工魚群算法適合描述團體逃生、小群體聚集行為；人工蜂群算法適合描述引導行為；蝙蝠算法適合描述親情行為、對出口有感知力的人群(如引導者)行為等。因此，本文在構建人群疏散模型時，將人群分類，并嘗試綜合使用多種群智能算法對各類人群進行建模，以使模型更加符合實際。

除此以外，疏散過程中的恐慌情緒會導致一系列混亂無序的非適應性行為，增加踩踏等事故發生的可能，同時人群也會自發產生小群體聚集等自組織行為，對疏散起到積極的作用。因此，疏散人群的混亂與有序程度會對人群疏散的效率、安全性等產生重要影響，然而現有模型較少考慮這一因素，也較少將定量表征混亂程度的疏散熵[10]用于構建人群疏散模型。因此本文在人群疏散模型中引入描述人群混亂程度的疏散熵模型，使模型更加貼合實際，更具實際指導意義。

1 相關方法

1.1 蝙蝠算法

蝙蝠算法是一種高效的生物啟發式優化算法，其模擬了蝙蝠利用回聲定位來捕食獵物的行為[11]。主要包括位置更新、局部搜索和脈沖頻率與響度更新3個步驟。

1.1.1 位置更新

蝙蝠算法通過調整頻率、追尋全局最優蝙蝠來控制速度與位置的更新，公式如下：

fi=fmin+(fmax-fmin)β

(1)

(2)

(3)

式中：fi為蝙蝠i的脈沖頻率；fmin、fmax分別為頻率最小、最大值，且為常數；β為值在[0,1]之間的隨機函數；xi為蝙蝠i的位置；vi為蝙蝠i的速度；x*為整個空間具有最佳適應度的蝙蝠所在的位置。

1.1.2 局部搜索

若脈沖發射率較低，則在全局最優蝙蝠附近進行隨機搜索，公式為

(4)

式中∈為值在[-1,1]之間的隨機數，At為t時刻所有蝙蝠的響度平均值。

1.1.3 脈沖頻率與響度更新

蝙蝠在尋找獵物初期，脈沖發射率低、響度高，便于廣泛尋找。當感知到獵物后會提高脈沖發射率，降低響度，由廣泛搜索慢慢轉向向著目標前進。故隨著向最優解的靠近，脈沖發射率與響度按如下公式更新：

(5)

(6)

1.2 疏散熵

疏散熵由魏心泉等[10]在2015年提出，用于定量刻畫人群運動的混亂與有序程度。首先將疏散空間離散化成均勻網格，將每個離散網格里人群的速度方向和大小分別離散化成等間距的8個區間，得到群體速度方向和大小的離散化如圖1所示，其中Vmax為疏散個體前進的最大速度。

圖1 速度方向與大小的離散化

然后通過統計每個區間上的疏散個體總數計算疏散熵值。每個離散網格內群體運動速度方向熵值En1、速度大小熵值En2和總疏散熵值En計算公式為：

(7)

(8)

En=α1En1+α2En2

(9)

式中：N為每個離散化網格中個體的總數，ni為第i個速度方向區間上個體的總數，mj為第j個速度大小區間上個體的總數，αi為權重系數，一般設定α1=α2=0.5。

最后根據疏散熵的大小，將每一個離散網格的疏散熵值映射到疏散場景中，即可得到整個場景的疏散熵圖，整個求解過程如圖2所示。

圖2 整個空間疏散熵圖的求解過程

2 模型構建

目前疏散模型大多將人群視為無差別的個體，但實際上人群疏散是一個由不同行人組成的復雜系統。通過對真實疏散視頻中的行人行為進行研究發現，人群疏散過程中會形成自組織群組，普遍存在群組引導者、群組成員和離散人員3類人群[12-13]。因此為了使疏散過程更加符合實際，本文在構建疏散模型時將人群分為群組引導者、群組成員和離散人員。

2.1 群組劃分

本文采用DBSCAN(density-based spatial clustering of applications with noise)算法達到群組劃分目的。具體步驟如下：隨機選擇一個沒有被訪問過的個體，將所有在距離ε內的個體都視為鄰居點。若鄰居點不大于minpoints，則該個體標記為離散人員，否則將該點及鄰居點，以及鄰居點的鄰居點，即所有在ε臨域內的個體聚集為一個新群組。不斷重復該過程，直到所有個體都被訪問，即每個個體都被標記為屬于一個群組或為離散人員。

2.2 位置更新模型

在每個群體內部群組引導者一般始終在群組的前方引導其他人，因此基于人工蜂群算法，將適應度高的前百分比例per疏散個體確定為群組引導者、剩下的為群組成員。到目前為止，疏散環境中的人群被分為了群組引導者、群組成員和離散人員。

2.2.1 群組引導者位置與速度更新

群組引導者是指對疏散環境較為熟悉，對出口有較強感知，能夠快速向出口疏散的人員。蝙蝠算法模擬了蝙蝠通過回聲定位感知并捕食獵物的能力，十分適合模擬對出口感知力較強的引導者行為。因此群組引導者的位置更新機制基于蝙蝠算法，包含位置更新、局部搜索、脈沖發射率與響度更新3個步驟，并針對蝙蝠算法中不適用于人群疏散建模的部分進行改進，使模型更加合理。

1)位置更新。由于人每一步的前進距離是有限的，故將疏散個體的速度分為速度大小Si和速度方向Di=[Dix,Diy]T兩部分，位置更新公式如下：

(10)

(11)

(12)

(13)

式中s-Di為個體i的搜索方向。

3)脈沖發射率與響度更新。脈沖發射率與響度的更新公式同式(5)、(6)，表示疏散個體正向著出口堅定快速的前進。

2.2.2 群組成員位置與速度更新

群組成員對出口感知力弱，易受周圍人影響，在疏散過程中傾向跟隨他人一起疏散。人工蜂群算法基于蜂群采蜜行為，核心是分工與合作，觀察蜂受引領蜂指引得到蜜源信息進行采蜜[14]，與人群疏散中群組成員跟隨群組引導者疏散類似，因此群組成員基于人工蜂群算法進行位置更新。

群組成員基于輪盤賭算法選擇引導者進行跟隨，引導者適應度越高被選擇的概率越大，選擇概率公式為

(14)

式中：pc,i為群體c中群組引導者i被選擇的概率，fitc,i為群體c中群組引導者i的適應度，n為群體c中群組引導者的數量。

進而，群組成員跟隨選擇的群組引導者進行位置更新，公式為：

(15)

(16)

2.2.3 離散人員位置與速度更新

離散人員對出口感知力弱于群組引導者，不能馬上定位出出口位置，且距離群組有一定距離，需要依靠自身搜索出口進行疏散。故基于粒子群算法進行速度與位置更新[15]，公式如下：

(17)

(18)

2.3 疏散熵修正模型

疏散熵修正是指在得到的預計更新位置的基礎上，考慮混亂程度對疏散的影響，對群組引導者的位置進行修正，主要步驟如下。

1)判斷是否進行修正。是否進行疏散熵修正取決于疏散熵修正閾值。判斷個體相鄰的8個區域的疏散熵值是否都小于疏散熵修正閾值，若存在大于閾值的區域，則進行疏散熵修正，否則不進行修正。當個體周圍疏散熵值都較低時，表示周圍疏散環境較為穩定，不需要引導個體朝相對穩定的區域前進。

2)確定修正方向。若進行疏散熵修正，則選擇視野內疏散熵值最低的區域為修正方向。根據個體速度方向確定視野內的5個相鄰區域，選擇其中疏散熵值最低的區域為修正方向，若存在兩個及以上熵值同為最低的區域，則選擇速度夾角最小的區域。

如圖3所示，黑色箭頭為預計更新方向，藍色虛線箭頭為修正方向，1-5為視野內的5個相鄰區域。圖3(a)為個體選擇視野內熵值最低的區域為修正方向，圖3(b)為當存在多個熵值最低區域時，選擇夾角最小的區域為修正方向，圖3(c)為當個體相鄰區域熵值均小于疏散熵修正閾值時，不進行方向修正。

圖3 方向修正

3)確定修正參數。確定修正方向后，按照以下公式進行速度與位置的修正：

(19)

(20)

式中：e-Di為個體i進行疏散熵修正后的速度方向，e-xi為個體i進行疏散熵修正后的位置，c-Di為修正方向；ce為修正參數，表示參考修正方向的權重，根據是否看見出口確定，若個體不能看見出口，會傾向選擇穩定的區域進行疏散，此時ce=2，若個體看見出口，則會傾向于向著出口前進，此時ce=0。

2.4 避障機制

在得到疏散個體下一步的位置以后，需要判斷新位置是否可達，即新位置上是否存在靜態障礙物和其他疏散個體。若新位置存在障礙物，則需要進行避障。本文利用代價值確定下一步可接受的概率，當可接受概率為0時，即新位置不可接受，則采取避障措施[15]。

避障機制采用周邊搜索的方式。具體規則為：若新位置不可接受，則選擇下一步方向偏差-10°～10°的隨機角度為新方向，若此方向對應的位置仍不可接受，則再擴大10°，選擇下一步方向偏差-20°～20°的隨機角度為新方向……依次類推，直到下一步位置可達。

熵修正的混合人工蜂群-蝙蝠算法人群疏散模型流程如圖4所示。

圖4 熵修正的混合人工蜂群-蝙蝠算法人群疏散模型流程圖

3 仿真與分析

3.1 疏散環境與參數設定

疏散場景設定為40 m×40 m的單出口二維矩形區域，四周灰色部分為墻壁，紅色矩形為出口，并隨機放置了一些深灰色矩形和圓形障礙物，設定疏散人數為80人。參數的設定見表1。

表1 參數取值

3.2 群組疏散仿真效果

首先，不引入疏散熵修正模型，將本模型與文獻[15]中的PSO疏散模型(即所有個體為離散個體)進行對比，驗證群組疏散效果。將兩個模型的初始位置設為相同，分別試驗了200組取平均值，以減輕初始位置及群組分布隨機性的影響，得到表2。

表2 200組實驗結果對比

由表2可以看到，本模型的每個個體的平均疏散時間和疏散完成時間均小于PSO疏散模型，其中每個個體平均疏散時間減少5.3%，疏散完成時間減少7.76%。這說明相比每個個體單獨疏散，以合適的群組形式疏散可以提高疏散效率。

圖5為仿真過程圖，對比了PSO疏散模型和本模型的疏散過程。文獻[14]通過對真實疏散視頻中的行人行為進行研究，歸納了疏散過程中自組織群組的形狀特點：疏散群組多呈現隊列行或排行，群組內部有一定程度的彎曲且相對緊密。

如圖5可以看到，在疏散初期，相比PSO疏散模型，本模型出現了明顯的疏散群組，群組內部較為緊密；在疏散中期，本模型中的疏散群組呈現隊列形狀，群組后方的個體跟隨群組前方的引導者向出口前進，且群組內部有一定程度的彎曲，符合真實群組的疏散形狀；在疏散后期，由于人群在出口處聚集，群組被一定程度的沖散，但相比PSO疏散模型，人群更為緊密。兩個模型都復現了“出口拱形”現象，本模型中的疏散群組也符合真實群組的疏散形狀，證明了模型的有效性。

圖5 PSO疏散模型和本模型疏散過程對比

圖6為疏散空間中不同種類人群的變化趨勢。可以看到，群組個體的下降速度快于離散個體。在群組個體多于離散個體的初始條件下，出現了離散個體晚于群組個體疏散出去的情況。這說明在疏散過程中，群組成員在引導者的帶領下能迅速向出口處疏散，避免了尋找出口等造成的時間浪費，能一定程度上提高疏散效率。

圖6 疏散空間中不同種類人群的變化趨勢

3.3 疏散熵修正仿真效果

3.3.1 疏散熵修正閾值對疏散時間的影響

在相同設定下改變疏散熵修正閾值仿真50遍取平均值得到圖7。由圖7可以觀察出，整體上隨著疏散熵修正閾值的增大，疏散完成時間和每個個體平均疏散時間呈先減小后增大的趨勢，當疏散熵修正閾值為0.4時，疏散完成時間和每個個體平均疏散時間最小。

圖7 疏散熵修正閾值與疏散時間的關系

分析可知，當疏散熵修正閾值較小時，個體在前進時過多考慮疏散混亂程度的影響，即使前方不是特別混亂也會朝向混亂程度更低的方向前進，延長了疏散路線進而增加了疏散時間；隨著疏散熵修正閾值的提高，個體只有在前方特別混亂時才會進行速度修正，以避開混亂區域盡快到達出口；當疏散熵修正閾值較大時，個體基本不進行速度修正，即使前方混亂也會向其前進，進一步加劇了混亂程度，導致了疏散時間的增加。下面的仿真將疏散熵修正閾值設定為0.4。

3.3.2 引入疏散熵對疏散過程的影響

圖8對比了有無疏散熵修正對疏散過程的影響。疏散初期，兩個模型的差別不大，疏散個體的分布都較為分散，每個網格的疏散熵值較低，此時基本不進行疏散熵修正。疏散中后期，疏散熵修正的作用明顯起來，無疏散熵修正的模型，人群尤其是群組傾向于選擇圖8(b)中的紅色箭頭對應的路徑進行疏散，導致這條路變得擁擠；引入疏散熵修正后，后面的綠色和藍色群組中的引導者引導各自群組成員，向圖8(e)中的紅色箭頭對應的路徑疏散，有效避免了混亂擁擠，提高了疏散效率，也增加了疏散安全性，一定程度上避免了因擁堵造成的二次傷害。

圖8 疏散熵修正對疏散過程的影響

圖9(a)為疏散時間與總疏散熵值的關系，反映整體混亂程度的變化趨勢，圖9(b)為疏散時間與個體分布網格平均疏散熵值的關系，反映局部混亂程度的變化趨勢。下面分別分析總疏散熵值的變化趨勢、個體分布網格平均疏散熵值的變化趨勢、以及疏散熵修正對兩者的影響。

圖9 疏散熵修正對疏散混亂程度的影響

總疏散熵值在疏散前期迅速升高，中期在較高值處波動，后期逐漸降低。這是因為疏散前期群組成員迅速向各自的引導者靠近，運動方向不一致導致整體的混亂程度迅速上升；疏散中期人群逐漸聚集到出口附近，個體與個體、個體與障礙物相互作用，混亂程度較高；疏散后期隨著人數的減少總熵值逐漸降低。

個體分布網格的平均疏散熵值在疏散前期上升緩慢，中期持續波動并略微升高，后期劇烈波動下降。這是因為疏散前期人群整體分散，局部混亂程度較低；隨著人群的聚集，局部混亂程度升高；疏散后期人數較少且分布集中，局部混亂程度的變化變得敏感，波動劇烈。

結合兩圖來看，疏散前期，由于疏散熵修正未發揮作用，曲線高度重合；疏散中期，相比未引入疏散熵修正的模型，引入疏散熵修正的模型降低了混亂程度，局部混亂程度降低的更為明顯，這是因為經過速度修正后，疏散個體的分布更加均勻化，減輕了局部的擁堵混亂程度；疏散后期，引入疏散熵修正的模型剩余個體更少，整體混亂程度和局部混亂程度均低于未引入疏散熵修正的模型。

3.4 應用探討

人群疏散問題是關切民生安全的問題，需對應用問題進行考量。該模型可以為人群仿真推演系統提供模型參考，人群仿真推演系統可以模擬推演疏散全過程，并給出疏散方案。該系統的疏散模擬步驟如下：

1)確定事故發生點、疏散區域、疏散時間。

2)確定出口數量及分布，獲取疏散時間對應的疏散區域內疏散人群數量及分布。

3)對疏散過程進行推演仿真(該疏散模型可為本步驟提供模型參考)。

4)給出疏散過程及疏散方案。示意圖如圖10所示，可以查看人群的疏散路徑、每個時刻人群的疏散情況、每個出口所疏散的人數等具體疏散信息。

通過人群仿真推演系統進行仿真推演，具有很好的應用價值，探討如下：

1)安全評估。針對新建的建筑物、風景區、娛樂場所等等，通過仿真可以知道現布局的安全性如何，并可以通過仿真來改進布局提高安全性。

2)人群疏散演練預案。針對場景人員比較固定的區域，如學校、住宅區。在進行疏散演練前，可利用該系統進行仿真，確定較好的疏散方案，進而根據該疏散方案組織疏散演練。

3)疏散工具準備。通過仿真可以了解各疏散出口所疏散的人數、時間等信息，可以據此設計疏散預案，為每個出口提前準備合適的撤離交通工具類別(如公交、地鐵、出租車等)及數量。

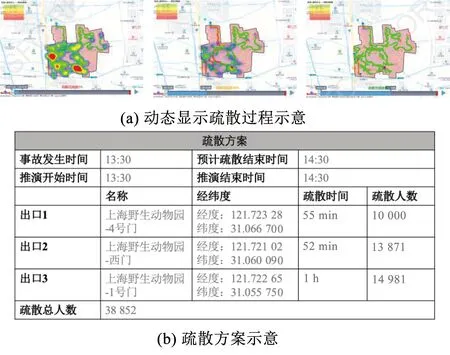
圖10 疏散過程及疏散方案示意

4 結 論

1)本文將疏散人群分為群組引導者、群組成員、離散人員3類以合理化疏散模型，并引入定量表征人群混亂程度的疏散熵模型，對模型進行了進一步的優化，構建了熵修正的混合人工蜂群-蝙蝠算法人群疏散模型。

2)仿真結果表明，該模型中的疏散群組較符合真實疏散群組的疏散形狀，以群組形式疏散可以減少疏散時間。引入疏散熵修正模型后，引導者可以引導群組成員避開混亂方向，避免擁擠造成的二次傷害，提高疏散安全性；同時，也避免了人群過度集中于某一條疏散路徑上，提高了空間利用率，一定程度提高了疏散效率。

3)本文雖然對應用方向進行了探討，但是并沒有針對具體的突發事件情境進行應用仿真分析，后續可對其進一步研究，使模型更具應用價值。