MRANS方案的反應堆壓力容器CFD仿真

康慧倫，田兆斐，胡培政，陳廣亮

(核安全與仿真技術國防重點學科實驗室(哈爾濱工程大學) 哈爾濱 150001)

作為堆芯的入口邊界，壓力容器下腔室出口的冷卻劑流量、溫度及硼的分布對反應堆的安全性和經濟性有著重要影響。因此，對壓力容器中冷卻劑流動特性進行研究成為反應堆安全分析的重要組成部分。隨著CFD技術的快速發展，利用CFD分析方法對壓力容器進行數值模擬，逐漸成為與實驗同樣重要的研究手段。中國核動力研究院的眭曦等[1]基于下腔室實驗對CFD計算中不同交混模型進行對比，認為組分輸運模型可以較好的描述由于濃度梯度導致的硼擴散現象。郭超等[2]基于CFX程序進行下腔室全尺寸計算，并對下腔室流場及壓力場進行研究，驗證下腔室流量分配設計合理性。Cho等[3]基于ROCOM實驗對CFD程序進行驗證，驗證結果表明CFD程序在適當的網格處理情況下可以合理的預測壓力容器內的硼稀釋現象。

大部分關于壓力容器的實驗的裝置按比例對真實壓力容器進行縮放，但其復雜的下腔室結構和依然較大的模擬域導致CFD模擬所需的網格數量龐大，對計算使用的硬件提出了較高的要求。同時，冷卻劑在壓力容器下降段與下腔室結構差異很大(下降段為環段結構，下腔室為球形且內含孔板結構)，使用同一湍流模型可能無法保證精度與效率的最佳平衡。為解決這些問題，本文將分段技術和MRANS方案應用在壓力容器CFD計算中。Navarro等[4]采用分段模擬技術對Karoutas等[5]的5×5棒束實驗進行模擬，以減少每次計算的計算負荷；Li等[6]對分段模擬技術在棒束通道仿真中的應用特性進行了研究；Chen等[7-8]針對帶交混翼棒束通道不同區域流體流動狀態不同的特點，基于分段模擬技術提出了多湍流模型(Multiple RANS models, MRANS)方案，在保證計算精度的同時提高計算效率，并提出了DP-CFD方案以解決堆芯大流域CFD仿真問題。值得注意的是，絕大部分的分段CFD分析技術和MRANS方案的討論都是針對棒束幾何模型，在其他幾何模型中的適用性仍然需要討論。

ROCOM實驗[9-10]被廣泛應用在CFD計算方法的驗證[11]中，許多學者基于ROCOM實驗裝置進行了CFD分析，其中包括網格敏感性、湍流模型和邊界條件效應等等[12-14]。本文以ROCOM實驗為對象，針對分段技術與MRANS方案展開研究，提出合理的分段計算與MRANS方案，減小計算負荷，提高計算效率，并保證CFD計算的準確性。

1 仿真對象介紹

本文以歐洲FLOMIX-R基準實驗中[9-10]的ROCOM實驗裝置為仿真對象，對穩態運行的壓力容器的冷卻劑交混現象進行研究。ROCOM實驗裝置以KONVOI三代壓水堆為原型，按1∶5的比例建造，反應堆壓力容器(RPV)為其主體設備，包括4個冷卻劑入口、出口、下降段(downcomer)及下腔室(lowerplenum)，下腔室布置有空心孔眼滾筒，堆芯入口布置支撐板。裝置具有4個完整的回路，并配有泵、閥門及蒸發器等設備，通過對泵的流量控制可以實現不同工況的實驗。在進行混合實驗時，實驗裝置在室溫和環境壓力下運行，示蹤劑氯化鈉溶液在入口上游注入主冷卻劑系統，并通過裝置進行混合，確保示蹤劑均勻分布在壓力容器入口橫截面處，壓力容器上布置有4處測點(容器入口、下降段上部、下降段下部及堆芯入口)對示蹤劑進行跟蹤，具體參數如圖1所示。

圖1 壓力容器及測點分布圖[5-6]

2 分段CFD技術研究

2.1 數值建模

2.1.1 幾何模型和網格劃分

根據Boumaza等[14]的研究，環路對發生在RPV的交混現象的影響很小。因此，在不影響計算準確性的前提下減少計算所需網格，本文使用300 mm的圓管代替環路作為RPV入口。堆芯采用高度為800 mm的圓柱代替，圓柱以堆芯入口支撐板上直徑30 mm的冷卻劑流量分配孔為基準進行延長。

圖2展示了本文所使用的網格模型。如圖2所示，本文采用多面體網格對RPV模型入口環腔和下腔室進行網格劃分，這是因為多面體網格與四面體網格相比，在達到相同精度的前提下具有更好的收斂性[6]。多面體網格的生成方式采用將四面體在FLUENT軟件中轉化的方式生成。下降段則采用六面體網格。表1展示了在網格敏感性分析中使用的不同劃分方案的網格量。圖3顯示了不同網格方案中堆芯入口處標量最大和平均值隨時間的變化趨勢。由于網格劃分占據了前處理中的絕大部分時間，同時無止境的增加網格量會增加大量的計算時間。因此，盡管未達到所謂的網格無關解，考慮精度與計算時間的平衡的情況下，本文選擇了方案2作為本文的計算網格劃分方案。

圖2 網格模型

表1 網格劃分方案

圖3 堆芯入口處標量最大值和平均值計算結果

2.1.2 邊界條件和湍流模型

本文以ROCOM_STAT_02實驗工況為仿真對象，其是針對低流速下的穩態混合進行的實驗，實驗過程中沒有發生熱傳導且操作環境為室溫和環境壓力，因此選擇25 ℃，1.01×105Pa的水作為計算工質，采用0.73 m/s(25%正常流速，即各環路的質量流率為46.25 m3/h)的均勻速度分布作為入口邊界條件，出口采用壓力出口邊界條件。作為硼替代物的混合標量采用均勻分布的方式由入口1中注入，注入時間共35 s。本文采用的時間步長與實驗中測點的時間監測間隔相同，均為0.05 s(頻率20 Hz)。本文的分段計算方案研究中,均使用RSM湍流模型。

2.2 分段方案研究

RPV根據流域特點可以分為：下降段(DC)和下腔室(LP)。在建模和網格劃分過程中，將DC和LP從整體RPV中拆分，得到代表各區域的獨立模型。本文利用FLUENT軟件帶有的界面數據讀寫功能，通過編寫的Python控制程序控制DC和LP之間的數據傳輸，完成分段計算的自動計算流程。圖4展示了DC和LP的數據傳遞過程。

圖4 分段計算的數據傳輸方案

在文獻[4,6-7,15]的分段計算中，將計算區域沿流動方向分為若干段，并將前一段的出口的速度場結果作為下一段的入口邊界條件，如圖4中黑線的傳輸方案。這種計算方式相當于把流場下游對上游的影響切斷，意味著假設了下游的幾何與流動狀態對上游沒有影響。這種數據傳輸方式可以保證在沒有回流模型中速度場的準確傳播，但由于缺乏下游模型，上游的出口壓力場將無法準確得到。綜上所述，由于缺少數據通信，會導致上游出口面與下游入口面的壓力分布不一致，無疑會引入一定的誤差。

針對上、下游交界面壓力不一致的問題，本文提出了一種基于區域重疊的雙向數據傳遞分段計算方案。區域重疊方案如圖5所示，DC域向下拉伸了150 mm的圓環柱與LP域重疊。在計算過程中，DC將LP的入口所在面的速度和其他標量數據作為入口邊界條件傳遞至LP，而LP將DC的出口所在面的壓力分布數據作為出口邊界條件傳遞至DC，其與文獻[4,6-7]的單向數據傳輸的不同之處在于數據傳輸包括了圖4中紅線的傳輸內容(壓力場)。圖6展示了不同的分段方案交界面處的壓力對比圖。

圖5 區域劃分方案

圖6 壓力分布對比

如圖6所示，相較于pressure-outlet出口邊界的均勻壓力場，outflow出口邊界的壓力分布在趨勢上與整體計算相似，這與Li等[6]所得到結果相同。然而，由于單向數據傳輸的自身缺陷，使用outflow邊界在交界面處的壓差與整體計算依然有一定差距(整體計算中界面壓力最高點與壓力最低點的壓差為100 Pa，而outflow計算為40 Pa)。而雙向數據傳遞的分段方案考慮了上下游的相互反饋，從圖6可以看出，雙向數據傳遞的分段方案與整體計算最接近。

圖7、8分別為不同的分段方案與整體計算的結果對比。圖7為DC下降段下部的3個測點的速度。考慮到計算幾何具有對稱性,3個測點選取在同一個象限內。圖8為LP中16號通道與42號通道堆芯入口平面的速度。選取這兩個通道是因為兩個通道分別在下腔室空心孔眼滾筒的內外兩側，具有一定的代表性。從圖中可以看出，采用雙向數據傳遞的分段方案與整體計算結果對比具有較好的一致性。

圖7 DC域中3個測點的速度

圖8 堆芯入口通道的速度

3 多湍流模型方案研究

3.1 MRANS方案設計

受到計算資源的限制，DNS和LES模型在工業CFD仿真領域使用較少，通常采用基于雷諾時均方法的RANS模型進行計算。雷諾時均的N-S(Navier-Stokes)方程可以表示如下：

(1)

(2)

標準k-ε模型(SKE)、realizablek-ε模型(RKE)、renormalization groupk-ε模型(RNG)及shear stress transportk-ε模型(SST)等2方程模型基于Boussinesq假設和湍流黏度的概念，通過下式求解雷諾應力。

(3)

式中：k為湍流動能,μt為湍流黏度。湍流黏度是湍流動能和湍流耗散率或比耗散率的函數，因此求解兩方程模型的雷諾應力需要建立湍流動能輸運方程和湍流耗散率或比耗散率輸運方程。

雷諾應力模型(RSM)摒棄了各向同性的湍流黏度概念，直接構造了關于雷諾應力的輸運模型，一般如下式所示。

(4)

式中：等號左側第1項為應力時間項,第2項為應力對流項,右側Dij為湍流擴散項,φij為壓力應變項,Gij為應力產生項,εij為耗散項。

經過模化后的雷諾應力模型中的雷諾應力為二階張量，需要求解6個雷諾應力分量方程和1個湍流耗散輸運方程。RSM模型在求解雷諾應力時需要建立更多的方程，導致其計算效率低于2方程模型，但由于RSM模型直接求解雷諾應力張量，可以更加準確的反應雷諾應力的各向異性，一般來說在復雜湍流應用中RSM模型的適用性和精確性優于兩方程模型[15]。

由于在RPV整個流域中，平均雷諾數達到了104量級，所以本文的多湍流模型方案選取SKE、RKE以及RSM這3個高雷諾數模型進行研究。上述3種模型有相同的壁面處理方式，可使用同樣類型與密度的網格對多湍流模型混合計算精度與效率進行對比分析。MRANS計算時需要在區域邊界面上對求解動量方程與湍流方程的重要參數數據進行傳遞，表2顯示了分段界面上各模型計算所需的參數。

表2 湍流模型參數

圖9、10為應用不同的湍流模型的計算結果與實驗值[11]的對比，分別對應著DC不同高度(upper和lower)測點的混合標量值。

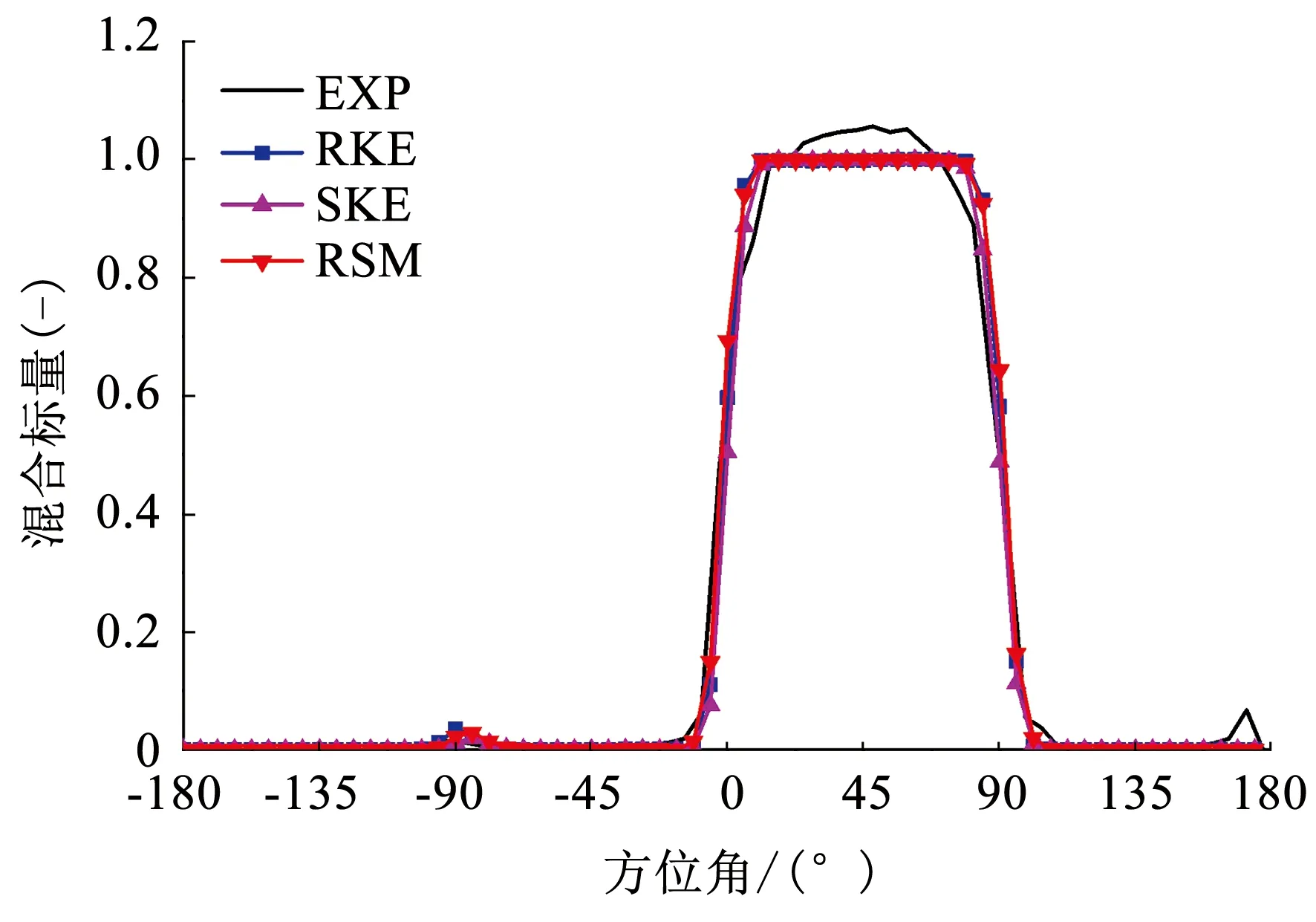
圖9 下降段上部測點標量方位角數據

圖10 下降段下部測點標量方位角數據

如圖9、10所示，在下降段上部2方程模型與RSM模型的計算結果差異很小且均與實驗值符合較好。在下降段下部，2方程模型預測的標量場空間分布的坡度比實驗值更加陡峭，而RSM明顯與實驗值的分布更加接近。可以看出，2方程模型明顯的低估了下降段湍流交混的能力，這可能是將各向同性的2方程湍流模型應用在具有高的各向異性的結構上所導致的。同時，這種交混能力的低估在很多的有關FLOMIX的結果中被發現[10]。

根據下降段的計算結果對比，本文基于SKE，RKE，RSM 3個模型進行互相匹配，設計多湍流模型耦合計算方案。因為多湍流模型計算方案的意義在于解決模擬大尺度部件時計算時間與計算精度難以平衡的問題，本文將遵循保證計算精度同時減小計算所需的資源的原則進行MRANS方案的設計。圖11為本文設計的MRANS計算方案，其中垂線連接的模型屬于單一模型計算方案，斜線連接屬于MRANS計算方案。通過各計算方案對整個流域的求解計算，可以從計算精度與效率兩個方面綜合評價MRANS方案與傳統方案的區別。從表2中可以看出，7方程模型包含有2方程模型所需要的全部參數，因此，在將7方程模型應用在2方程模型的上游時，無需補充參數。

3.2 MRANS方案驗證

根據圖11的MRANS計算方案，分別對5種SKE,RKE,RSM的單一/混合模型進行計算。作為下腔室的入口，下降段出口處的流場及標量場結果的準確性會對下腔室流場的計算造成極大的影響。圖12分別展示了MRANS方案和單一湍流模型方案在下降段下部測點預測的速度和標量。圖中黑色實線為實驗值，虛線為實驗值±30%范圍。圖12(a)中速度為z軸方向速度。如圖12所示，由于MRANS模型在下降段使用RSM模型進行計算，因此在下降段下部測點的速度分布與RSM模型計算結果高度一致。SKE模型和RKE模型的計算結果也表現出一致性。在速度分布的計算中，RSM模型和MRANS模型在大部分區域與2方程模型精度相差不大，但在峰/谷值處與實驗值更一致。

圖11 MRANS計算方案

考慮到下降段標量場的影響范圍，圖12(b)將標量未擴散的區域的數據予以剔除。相較于7方程模型，單一的兩方程模型低估了低濃度區域的混合標量濃度，并且高估了高濃度區域的混和標量濃度。這與圖10的計算結果相符合。RSM的混合標量預測結果與實驗值符合最好，而MRANS模型也僅在極少的位置與RSM模型有差異。無論是速度場還是標量場，MRANS模型都展現出了比SKE或RKE更優秀的精度。

圖12 下降段下部測點的速度與混合標量

圖13、14展示了不同RANS方案的RPV堆芯入口第16號和第25號通道的標量濃度的計算結果。在靠近下降段的第16號通道，單一的SKE和RKE模型預測的混合標量濃度上升非常迅速，在10 s內達到了充分混合的平穩階段(在實驗中上升過程約為15 s)，且過高的預測了平穩階段的混合標量濃度。相較于2方程模型，RSM模型在上升階段和平穩階段的預測結果均與實驗符合較好，兩種MRANS方案中RSM-SKE模型在16通道均與RSM模型符合較好，且能較準確的描述標量隨時間的變化過程。單一的SKE和RKE模型計算結果相類似，在上升階段和平穩階段預測結果與實驗值的平均偏差分別為32%和17%，MRANS模型為11%和9%，RSM模型為5%和7%。而在相對更靠近中心的25號通道，單一的兩方程模型預測的上升過程與實驗符合較好，但仍低估了平穩階段的標量濃度。所有的模型在上升階段的預測與實驗的平均偏差都在10%左右。在平穩階段，單一的SKE和RKE模型的平均偏差為19%，MRANS模型為11%，RSM模型為5%。兩種MRANS方案在上升階段和平穩階段的前半段預測符合較好，但在平穩階段的后半段的混合標量濃度預測較RSM仍有較大偏差。之所以產生這種情況是因為，16通道為邊緣通道，靠近下降段，流體從下降段進入下腔室后迅速進入通道，因此MRANS方案對該區域的準確性的提升較大。而25通道為中心通道，流體進入下腔室后需要流經分配孔板等幾何結構后才能進入通道，因此MRANS方案對該區域的提升較小。

圖13 堆芯入口第16號通道的標量隨時間變化

圖14 堆芯入口第25通道標量隨時間變化

通過上述分析可以看出，基于RSM模型的MRANS方案可以得到與單一RSM模型符合較好的計算結果。由于不是全域使用更耗時的RSM模型，采用MRANS方案減少了大量的計算時間。表3為本文所設計的MRANS方案與單一的RSM模型在Inter(R) Xeon(R) CPU E3-1280 v5，3.7 GHz，64 G的單機8核處理器條件下的計算效率。如表3所示，MRANS方案相較于單一的RSM模型更加高效，在本文的網格規模下可以縮短約30%的CPU時間，且隨著網格數量增加或LP網格數量在整體RPV模型的比重增加，可以增大這種MRANS方案的優勢。

表3 MRANS計算方案與RSM方案計算效率

4 結 論

1)本文將棒束CFD分析中提出的分段方案運用到壓力容器CFD分析中，設計了基于區域重疊方法的雙向數據傳遞分段計算方案。

2)分析了不同的湍流模型在各區域的計算結果，為分區計算選擇合適的湍流模型。

3)通過運用MRANS方案和所設計的雙向數據傳遞分段計算方案構建了SKE-RSM與RKE-RSM兩種MRANS方案，相比于傳統的單一RSM湍流模型計算方案，本文提出的MRANS方案具有更高的效率。研究成果對提高RPV CFD仿真效率提供了一種新思路和途徑。