有偏置的Rabi模型的能譜與Berry相

于 婷 任學藻

(西南科技大學理學院 四川綿陽 621010)

在量子力學中，波函數的相位問題一直是很重要的概念。幾何相位近幾年受到國內外學者的大量關注。幾何相位這一定義最初是由印度物理學家Pancharatnam[1]在1956年研究偏振光干涉的時候提出來的，但在當時并沒有引起大家重視。1984年，英國物理學家Berry[2]發現，系統的哈密頓量在絕熱循環演化過程中，量子態除了產生一個一定存在的動力學相位之外，還產生了一個只與系統空間演化路徑有關的幾何相位，這就是現在的Berry相，從此Berry相被廣泛接受和深入研究。1987年Aharanov等[3]對Berry相做了推廣，提出絕熱并不是必要條件，波函數在非絕熱循環演化過程中依舊會獲得一個幾何相位。1988年，Bhandari等[4]通過研究發現在非循環非幺正的量子體系中也存在Berry相。隨著量子信息技術的高速發展，1999年，Zanari[5]提出Berry相可用于量子計算，接著Jozsa等[6]在2000年通過核磁共振技術證實了幾何量子計算的可靠性。在物理學家們對Berry相的不斷深入研究中，已經認識到了它的獨特性和在量子理論中的重要性。Jaynes-Cummings模型在之前一直被認為是在量子光學系統里描述光與原子相互作用最簡單解析求解的模型，但后來人們發現該模型的局限性，J-C模型作的旋波近似處理方法[7]在強耦合時會帶來錯誤的計算結果。這是因為，在光與物質強相互作用下，反旋波項無法忽略，這時就需要用非旋波近似的Rabi模型[8]來展開計算與研究。2012年，Jonas[9]通過半經典近似的方法，發現非旋波近似Rabi模型沒有Berry相，進而說明量子系統的Berry相是由旋波近似帶來的一種誤差。但這一結論很快被證實是不正確的。我們注意到Rabi模型的基態不是真空態，而是各種態的疊加，并且從理論推導中可以發現Rabi模型的Berry相與本征態下光子數的期望值成正比[10-12]，所以Jonas認為Rabi模型沒有Berry相的結論是由于他采用了不適當的近似方法所導致的。我們將Rabi模型推廣加上了偏置項，即模擬外加電場對量子比特的調控，并通過調整耦合強度的大小進行對比分析，觀察Berry相位差的變化，探討偏置項對Berry相的影響，這對于在量子模擬或量子計算中量子比特系統的調控具有重要意義[13]。

1 模型與推導

1.1 Rabi模型的Berry相

當單模光場與二能級原子作用時，Rabi模型的哈密頓量為:

(1)

其中:ω0為光場頻率;a+(a)為光子的產生(湮滅)算符;ω為二能級間距;σz為自旋1/2的pauli矩陣;σ+和σ-是升降算符;g為耦合強度。

將式(1)用矩陣表示為:

(2)

為了方便計算，我們對哈氏量旋轉90度，用下面的旋轉變化來實現：

(3)

V+σzV=σx,V+σxV=-σz

(4)

因此旋轉后的Rabi模型可以寫成如下形式：

(5)

根據光子數態，具有一般廣泛形式的奇偶宇稱下的本征函數為:

(6)

其中:φ+(φ-)對應偶(奇) 宇稱下的本征函數；M為截斷數。很容易驗證上述態是宇稱算符的本征態。考慮宇稱對稱的波函數將極大簡化求解過程[11-12]。

將式(6)代入薛定諤方程式(5)很容易得到系數之間的關系：

(7)

左乘〈m|，并考慮到Fock態的正交歸一條件〈m|n〉=σmn，得到：

(8)

下面我們將方程式(8)寫成矩陣形式：

(9)

(10)

其中：|g〉,|e〉分別表示原子的基態和激發態；|n〉為光場的Fock態。

對于不含時的哈密頓量的物理系統，Berry相的計算通常要引入一個相位轉換算符U(φ)=e-iφa+a絕熱地加在系統的哈密頓量上[14]，它能夠導致場態的改變。當系統初態為本征態時，且參數φ從0～2π 絕熱的變化時，Berry相可由下式給出：

(11)

(12)

1.2 有偏置項的Rabi模型的Berry項

我們將Rabi模型推廣加上偏置項，可以在量子計算中得到更廣泛的運用，該模型的哈密頓量為：

(13)

其中：ω0為光場頻率；a+(a)為光子的產生(湮滅)算符；ω為二能級間距；σz為自旋1/2的pauli矩陣；σ+和σ-是升降算符；g為耦合強度；ε為偏置項的系數。

Rabi模型的哈密頓量的本征態的一般形式可表示為：

(14)

其中：|g〉,|e〉分別表示原子的基態和激發態；|n〉為光場的Fock態。

將式(14)展開：

(15)

(16)

同樣地，把一個相位轉換算符U(φ)=e-iφa+a絕熱地加在系統的哈密頓量上[14]，使參數φ從0～2π絕熱地變化，當系統初態為能量本征態|Ψj〉時，Berry相為：

(17)

2 模擬與討論

2.1 偏置系數對能譜的影響

取Rabi模型的4個能量較低的本征態，圖1顯示它在不同失諧量時能譜隨耦合強度的變化，其中紅色對應偶宇稱，藍色對應奇宇稱；黑色對應偏置系數ε=0.1時的Rabi模型的能譜；紫色對應偏置系數ε=0.6時的Rabi模型的能譜。本文中ω0=1，失諧量Δ=ω-ω0。

從圖1可以發現，在Rabi模型中，不論是共振還是失諧的情況下，它的能譜都幾乎隨耦合強度g的增加而單調下降，不同宇稱相鄰兩能級的能譜曲線會隨g的取值范圍的變大而逐漸重合，而且奇偶宇稱的相鄰能級的激發態會發生能級交叉現象，同宇稱的能譜一般不相交，只有不同宇稱的能譜才會相交。只有在共振且g=0時，奇宇稱相鄰兩能級的能譜才有交點。加小偏置(ε=0.1)時，它與Rabi模型的能譜基本重合，但是它的各級能譜曲線都不相交，特別是在Rabi模型能級交叉的簡并點附近，它的能級結構發生了很大變化，在這里簡并點的能級被打開，偏置項的存在破壞了Rabi模型的奇偶宇稱。觀察該簡并點位置發現：圖1(a)顯示在共振Δ=0時，簡并點在g=0.48左右；圖1(b)顯示在失諧量Δ=-0.5時，簡并點在g=0.50左右；圖1(c)顯示在失諧量為Δ=0.5時，簡并點在g=0.35左右。所以，該能量簡并點的耦合強度會隨失諧量的增加而減小。加大偏置(ε=0.6)時，各級能譜都不相交，呈單調遞減趨勢，并且隨著正失諧量的增大，第二三能級的能譜在低耦合區(g≤0.30)會逐漸重合。

圖1 Δ=0,-0.5,0.5情況下 Rabi模型(ε=0，0.1，0.6)的能譜的Ej/ω0關于g/ω0的函數Fig.1 Energy spectra Ej/ω0 of the Rabi model(ε=0，0.1，0.6) as a function of g/ω0 when Δ=0,-0.5,0.5

2.2 偏置系數對Berry相的影響

圖2 Δ=0,-0.5,0.5情況下 Rabi模型(ε=0，0.1，0.6)的Berry相(γj)關于g/ω0的函數Fig.2 Berry phase (γj) of the Rabi model(ε=0，0.1，0.6) as a function of g/ω0 when Δ=0,-0.5,0.5

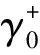
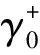
3 結論

在Rabi模型中，對于能譜，無偏置時奇偶宇稱的相鄰激發態能級會交叉，相同宇稱的能級一般不會交叉，而有偏置時，所有能級都不會交叉。對于Berry相，在Rabi模型(ε=0)中，不同宇稱的相鄰兩能級的Berry相會逐漸趨于一致，在加小偏置(ε=0.1)的Rabi模型中，j由小到大兩相鄰能級的Berry相會逐漸趨于一致，并且與Rabi模型的Berry相對比，除簡并點附近基本一致，在能量簡并附近的Berry相變化較大，這是由于Rabi模型系統的奇偶對稱性被偏置項所破壞，宇稱不再守恒所導致的。在加大偏置(ε=0.6)的Rabi模型中，當j≠0,2時，j由小到大相隔兩個能級的Berry相會兩兩趨于一致，基態的Berry相與無偏置時基本相似，但高能級的Berry相與無偏置時有很大不同，說明偏置項的存在對高能級的Berry相影響較大。值得注意的是，當共振時，在弱耦合到強耦合變化的范圍內，Rabi模型的所有激發態與基態的Berry相位差發生了π的奇數倍的改變，而加了偏置后所有激發態與基態的Berry相位差發生了π的偶數倍的改變，這在量子計算和量子模擬中具有重要意義。