基于DWT-WFGM(1,1)-ARMA組合模型的農業用水量預測

王冠智，粟曉玲*，張特，姜田亮，褚江東

基于DWT-WFGM(1,1)-ARMA組合模型的農業用水量預測

王冠智1,2，粟曉玲1,2*，張特1,2，姜田亮1,2，褚江東1,2

（1. 西北農林科技大學 水利與建筑工程學院，陜西 楊凌 712100；2. 西北農林科技大學 旱區農業水土工程教育部重點實驗室，陜西 楊凌 712100）

農業用水量預測對于區域水資源規劃與管理具有重要意義。【】針對農業用水量序列的振蕩性以及傳統模型預測結果輸出單一的問題，提出一種新的組合預測模型DWT-WFGM(1,1)-ARMA對區域農業用水量進行預測。通過離散小波變換將原始用水量序列分解為近似序列和細節序列，并分別采用自回歸滑動平均模型和分數階灰色模型預測細節序列和近似序列，并結合加權馬爾可夫鏈對近似序列進行誤差修正，將不同成分序列的預測結果進行線性疊加得到農業用水量的預測值和預測區間。利用該模型分別對陜西省和內蒙古自治區的農業用水量進行預測，并與灰色模型GM(1,1)、DWT-GM(1,1)-ARMA模型和DWT-FGM(1,1)-ARMA模型對比分析。DWT-WFGM(1,1)-ARMA模型在陜西省和內蒙古自治區的評價指標平均絕對百分比誤差分別為1.25%和1.01%，預測精度高于其他模型，且預測區間為研究區未來時期的農業用水量提供了合理的波動范圍，具有一定的實際參考價值。本文構建的組合模型能夠有效提高農業用水量預測的精度，同時預測區間的提出可以為區域農業用水量預測提供更加可靠的依據。

農業用水；分數階灰色模型；加權馬爾可夫鏈；離散小波變換；預測區間

0 引 言

【研究意義】農業用水是國家糧食安全的重要保障[1]。近年來，隨著社會經濟發展和城市化進程的加快，工業和生活用水量逐年增加，農業用水的供需壓力不斷增大。同時，由于人們對水資源規劃的重視程度不足，導致灌溉用水效率低下與農業用水短缺等問題并存[2]。農業用水預測是進行水資源規劃、配置和管理的工作基礎，準確預測農業用水量可以為區域水資源的高效管理與合理配置提供有力的支撐。

【研究進展】農業用水量預測方法眾多，其中定額法、時間序列法、神經網絡法以及灰色模型等方法已得到廣泛的應用[3-5]。農業用水量受氣候變化、經濟發展、科技進步等多方面因素的影響，序列通常呈現振蕩趨勢，單一模型難以體現其非線性特征，影響預測精度[6-8]。組合模型結合多種模型的優勢，可有效提高預測結果的準確性[9]。在用水預測組合模型中，小波變換與其他方法的耦合模型取得了較好的預測效果[10-12]。其中，最常見的小波組合模型DWT-GM(1,1)-ARMA通過小波分解將振蕩序列的預測轉化為灰色模型（Grey Model，GM(1,1)）與自回歸滑動平均（Autoregressive Moving Average Model，ARMA）模型的分量預測。如佟長福等[10]構建DWT-GM(1,1)-ARMA模型對中國農業需水量進行預測，取得了較好的精度；鄧權龍等[11]對礦區用水量預測的研究結果也表明該模型具有良好的預測性能。【切入點】然而，農業用水量的影響因素具有階段性，使得用水序列在不同時段呈現出不同的變化趨勢，而灰色模型GM(1,1)在分量預測過程中對各時段的用水序列信息賦予相同權重，無法準確反映用水變化的內部規律，樣本中的數據信息未得到充分挖掘[13-14]。分數階灰色模型（Fractional Order Grey Model，FGM(1,1)）是在GM(1,1)模型基礎上提出的新型灰色預測模型，具有新信息優先、預測擾動小等特點，廣泛應用于眾多領域的預測工作中[15-17]，而目前尚未引入用水量的預測研究。此外，DWT-GM(1,1)-ARMA模型僅以預測值作為模型的輸出結果，而單一的預測值無法提供更多的信息，模型有待進一步改進。

【擬解決的關鍵問題】針對農業用水量序列的振蕩性以及傳統模型預測結果輸出單一的問題，本文在DWT-GM(1,1)-ARMA小波組合模型的基礎上，將離散小波變換（Discrete Wavelet Transform，DWT）、加權馬爾可夫鏈（Weighted Markov Chain，WMC）、改進的分數階灰色模型（WFGM(1,1)）和自回歸滑動平均模型相結合，提出DWT-WFGM(1,1)-ARMA組合模型，并應用于陜西省和內蒙古自治區農業用水量預測中，以期為農業用水規劃提供技術支撐。

1 研究區域和數據來源

農業用水（包括農田灌溉及林牧漁畜用水）為陜西省（31°42′—39°35′N，105°29′—111°15′E）和內蒙古自治區（37°24′—53°23′N，97°12′—126°04′E）的主要用水戶，分別占兩省總用水量的60%和70%以上。本文以這兩省區的農業用水為研究對象，對農業用水量進行預測。歷史用水數據分別來源于兩省區2002—2019年的水資源公報。

2 研究方法

2.1 離散小波變換

小波變換是一種時頻信號局部化分析的方法，通常分為連續小波變換（CWT）和離散小波變換（DWT）2類[18]。由于時間序列一般是離散的，實際應用中經常采用離散小波變換：

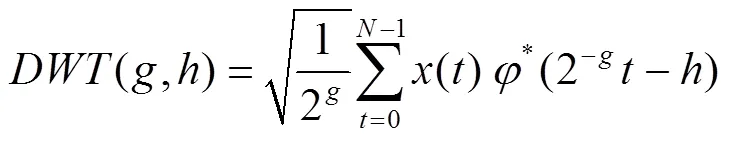
式中：()為時間序列；為序列長度；*()為小波函數()的共軛復數；(,)為離散小波系數，為確定小波伸縮與平移幅度的整數。

通過離散小波變換對原始序列進行分解得到反映序列趨勢性的近似序列A和由隨機成分構成的細節序列（1、2,…,D）二部分，如圖1所示。

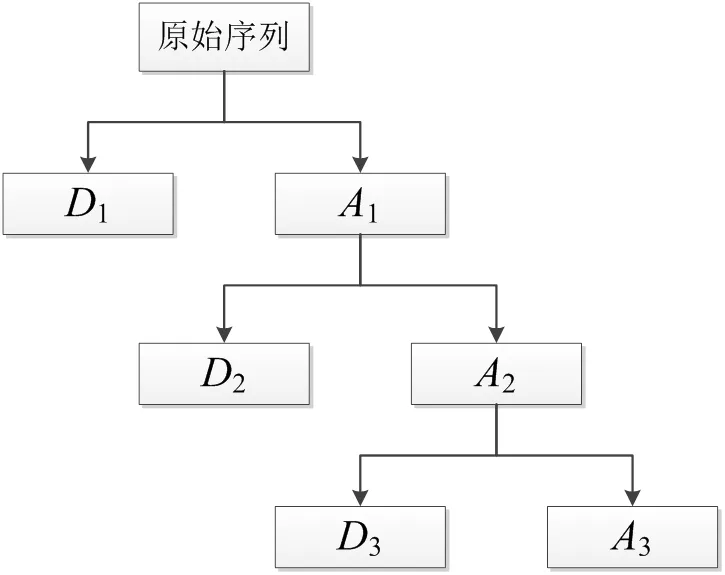
圖1 三層離散小波變換

在小波函數選擇上，Daubechies（dbN）小波具有正交性、高正則性等特點，在非平穩序列的分解上具有較好的效果；在分解層數選擇上，小波分解層數越多，序列的平穩性越好，但由于分解過程存在誤差，層數越多，誤差越大，因此分解層數一般采用2～4層[19]，本文選取為3層。

2.2 分數階灰色預測模型FGM(1,1)

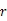
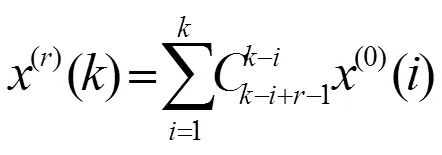
模型時間響應式為：

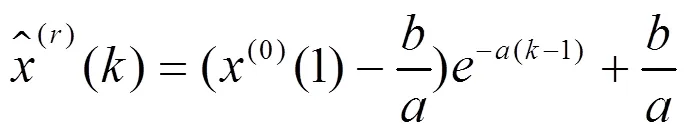
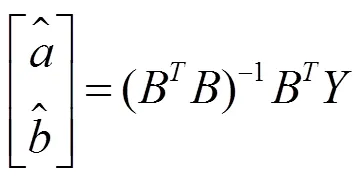
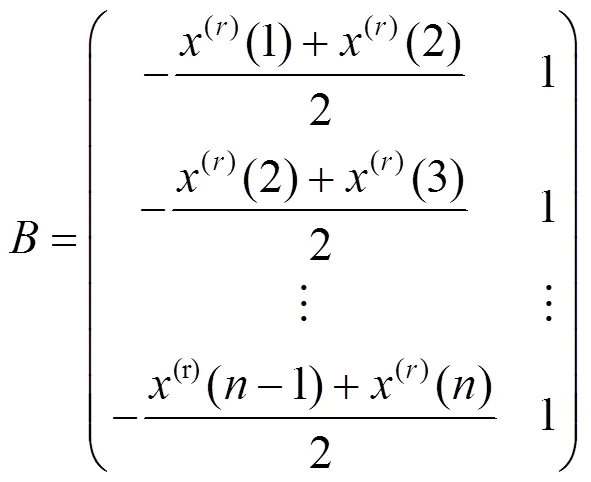
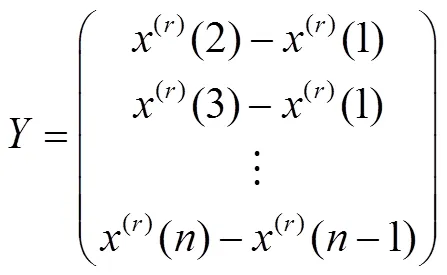
分數階灰色模型FGM(1,1)的階數對模型的預測性能有較大的影響，為了獲得最優階參數，通常以“最優擬合”為優化目標函數：

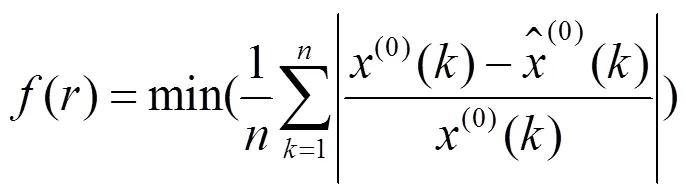
式中：()表示模型對歷史序列的擬合程度。

2.3 基于加權馬爾可夫鏈修正的分數階灰色模型WFGM(1,1)

為了最大程度挖掘近似序列中的有效信息，本文將加權馬爾可夫鏈理論應用到分數階灰色模型預測中，修正分數階灰色模型預測的結果，達到改善模型預測精度的目的。

2.3.1 FGM(1,1)模型誤差狀態區間的劃分

FGM(1,1)模型預測值與序列實際值的相對誤差（=12,…,）呈非規律性變化，將劃分為個狀態區間，任意誤差狀態區間可以表示為：

式中：E為第種狀態，2i和1i分別為E狀態的上、下界。

采用最優分割法對誤差狀態區間進行劃分，以“組內差異最小、組間差異最大”為劃分依據，通常定義分類誤差函數為：

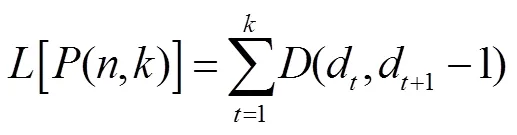
式中：為樣本數目，為狀態區間的分類數目，(d,d+1-1)為樣本的離差平方和，具體計算可參考文獻[21]。其中，通常通過[(,)]曲線圖確定，曲線拐點處的即為狀態區間的最優分類數目。

2.3.2 自相關系數和權重的計算

設狀態E出現的次數為S，由狀態E經過步到狀態E的次數為S，則由狀態E到E的轉移概率為：

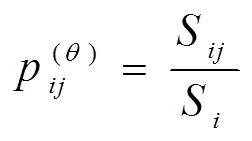
得到×階的狀態轉移概率矩陣()，記作：

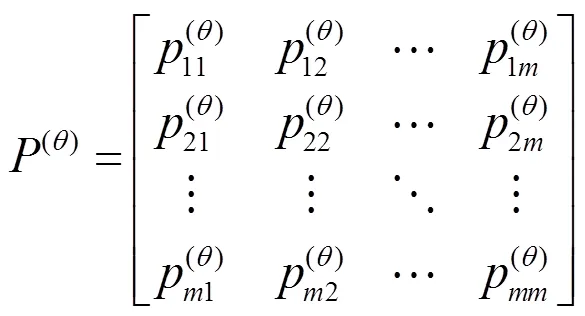
為反映各階步長對馬爾可夫鏈修正值的影響權重，采用的各階自相關系數反映權重的大小：

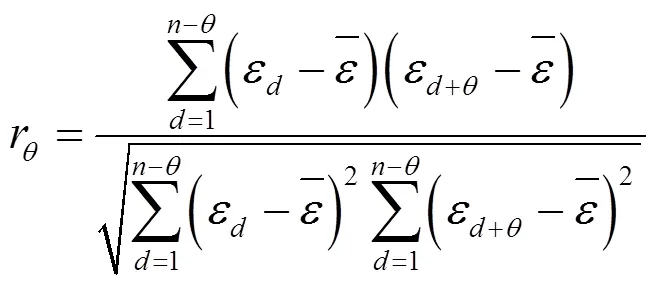
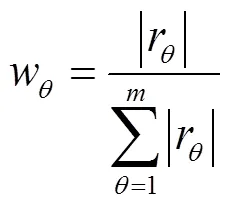
2.3.3 WFGM(1,1)模型預測

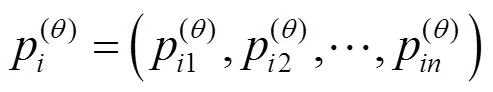
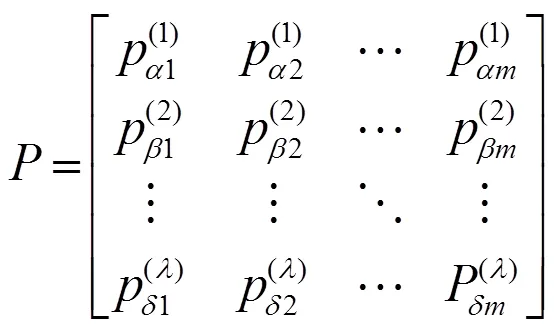
式中：,,∈,,,≤。

將同一狀態下的各轉移概率加權和作為預測相對誤差d的轉移概率：

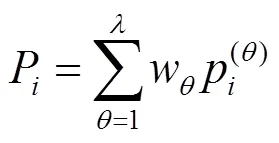
取P最大值所處的狀態即為下一階段預測相對誤差d的加權馬爾可夫狀態。以此類推，可得到未來多年的預測誤差區間，根據誤差區間的中值和邊界值可得到近似序列的預測值()和預測區間()：

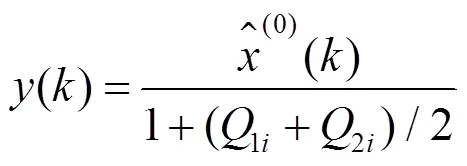
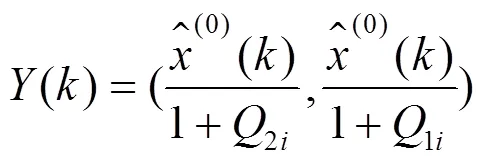
2.4 自回歸滑動平均模型（ARMA）

ARMA模型廣泛應用于時間序列的預測分析，模型不僅能夠有效地捕捉離散小波分解后時間序列的隨機成分，同時具有結構簡單、高效等優點，對細節序列預測具有良好的適用性，ARMA(,)模型計算式為：

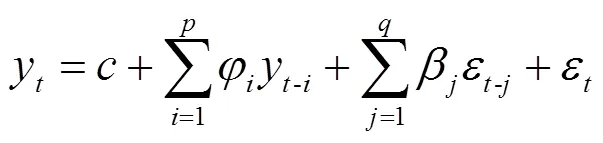
2.5 DWT-WFGM(1,1)-ARMA模型

農業用水組合預測模型由離散小波變換、加權馬爾可夫鏈修正的分數階灰色模型和自回歸滑動平均模型組成。通過離散小波變換對原始序列進行分解，并對分解后的2種成分序列分別采用不同的方法進行預測。具體步驟如下：

步驟1：采用離散小波變換對原始用水序列進行處理，得到一個近似序列A和若干個細節序列（1,2…,D）。

步驟2：對近似序列A采用基于加權馬爾可夫鏈修正的分數階灰色模型WFGM(1,1)進行預測。首先，以“最優擬合”為準則計算得到模型最優階數（當=1時，FGM(1,1)模型轉化為GM(1,1)模型），在最優FGM(1,1)模型預測得到初步預測值后結合加權馬爾可夫鏈劃分序列的誤差區間，推求未來用水序列所處的誤差狀態區間，并根據預測誤差狀態區間的中值和邊界值求得近似序列A的預測值及預測區間，預測值和預測區間的計算式見式（16）和式（17）。

步驟3：對于細節序列1、2,…,D，根據赤池信息準則（Akaike information criterion，AIC）建立ARMA模型進行預測，具體見式（18）。

步驟4：將細節序列和近似序列的預測結果線性疊加，得到最終的預測值和預測區間。

模型詳細操作流程如圖2所示。

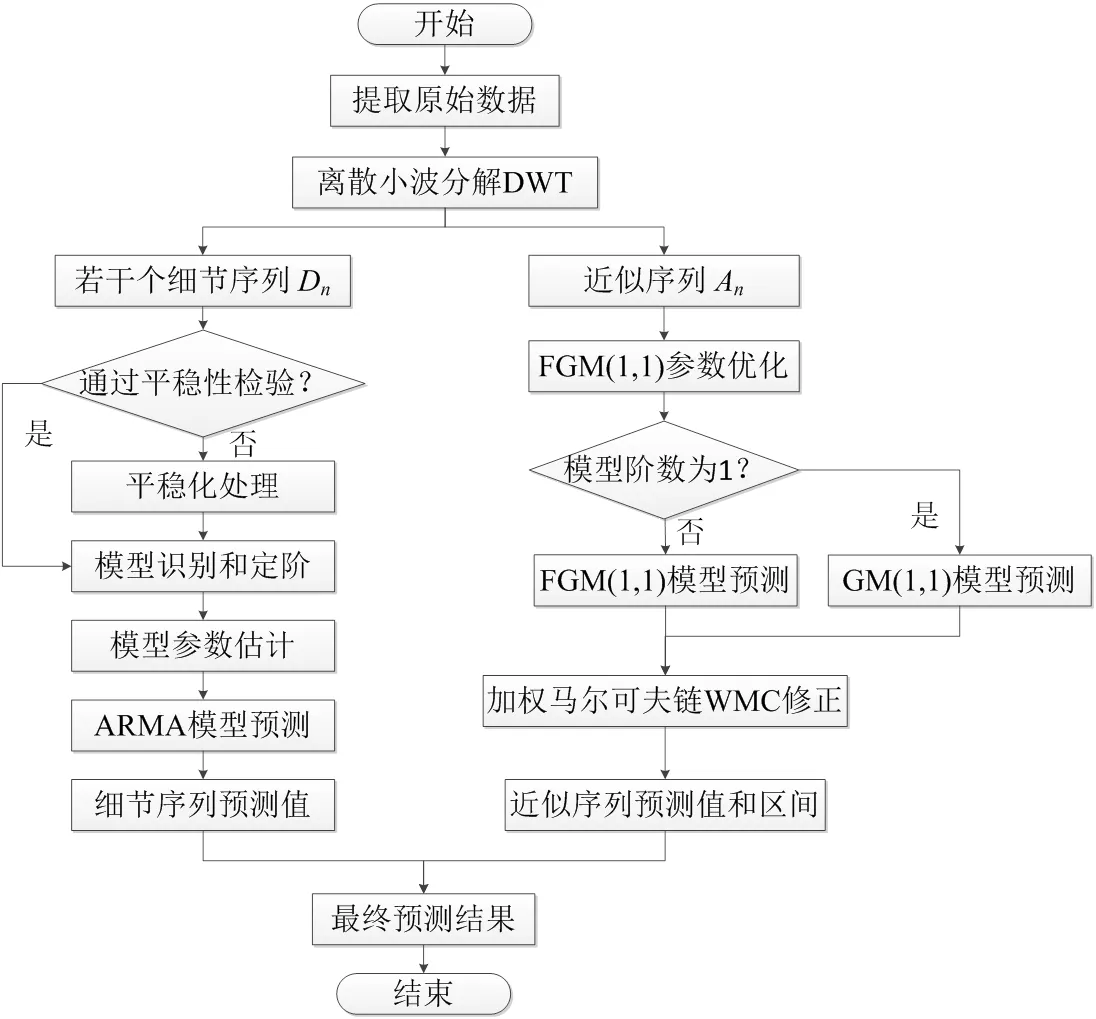
圖2 基于DWT-WFGM(1,1)-ARMA的農業用水預測模型流程

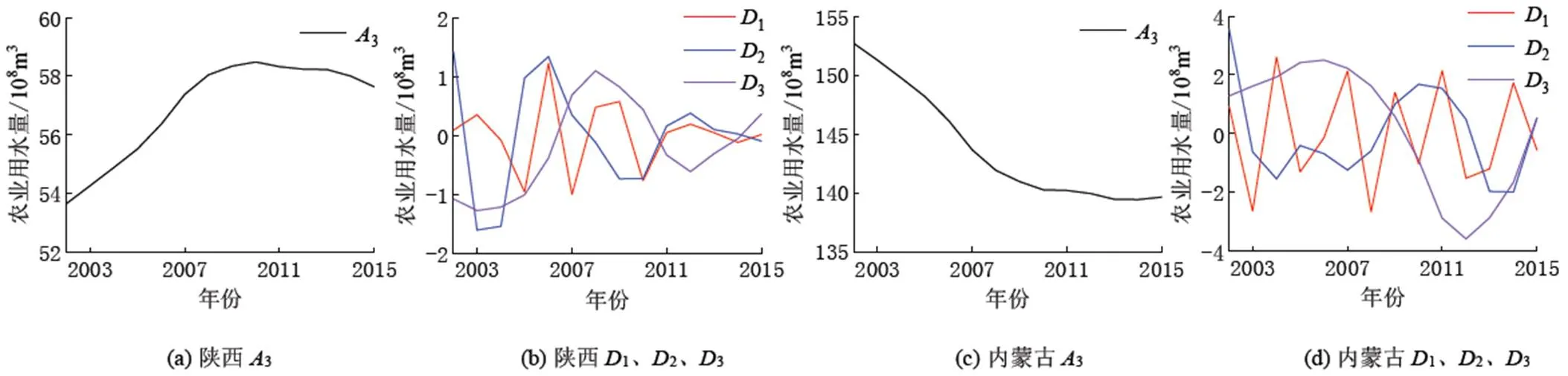
圖3 農業用水序列成分分解結果

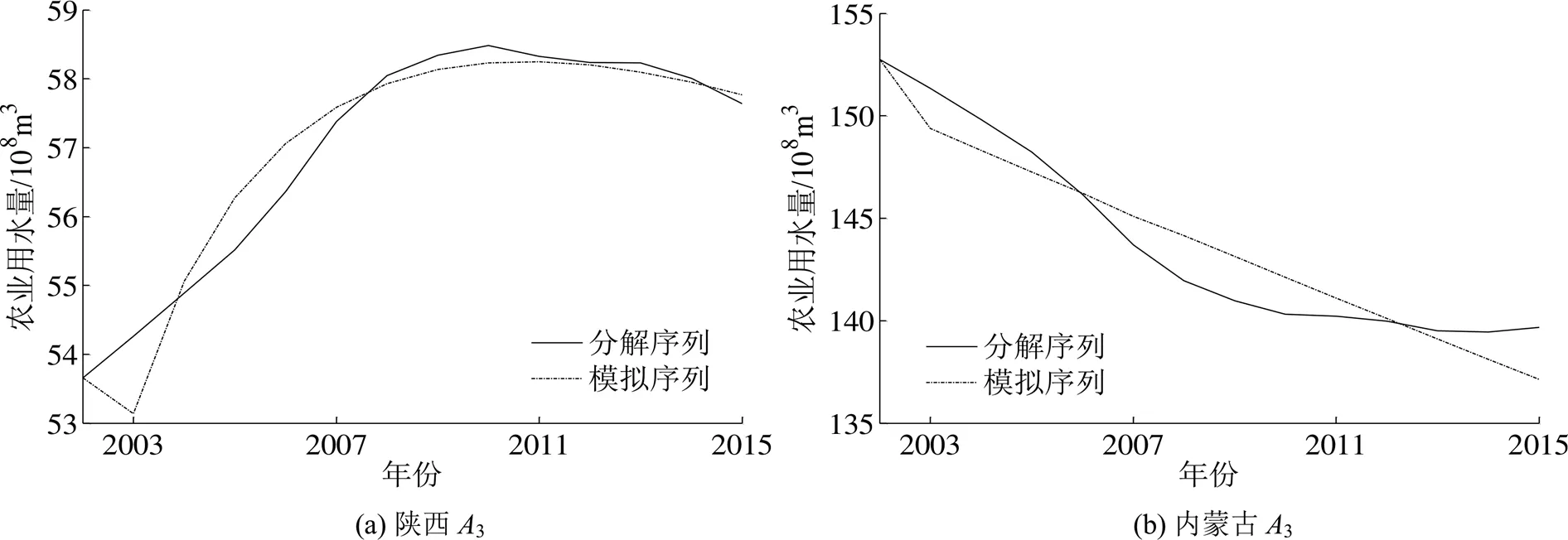
圖4 近似序列A3擬合結果

3 模型應用和結果分析

以2002—2015年為模型訓練期，2016—2019年為模型驗證期，并選擇均方根誤差（）、平均絕對誤差（）和平均絕對百分比誤差（）作為模型精度的評價標準。

3.1 離散小波分解

根據農業用水的序列特征，采用db4小波對原始序列進行3層分解，分別得到陜西和內蒙古二省區原始序列時間尺度為3的近似序列3和細節序列1、2和3，見圖3。

3.2 近似序列預測

3.2.1 最優階數的確定

確定FGM(1,1)的最優階數需要進行大量計算，本文采用粒子群優化（PSO，Particle Swarm Optimization）算法對模型階數進行計算。結果表明，當陜西省和內蒙古自治區的模型階數分別為0.893 3和1.0時，模型在訓練期的模擬效果最好，如圖4所示。

3.2.2 加權馬爾可夫鏈修正分析

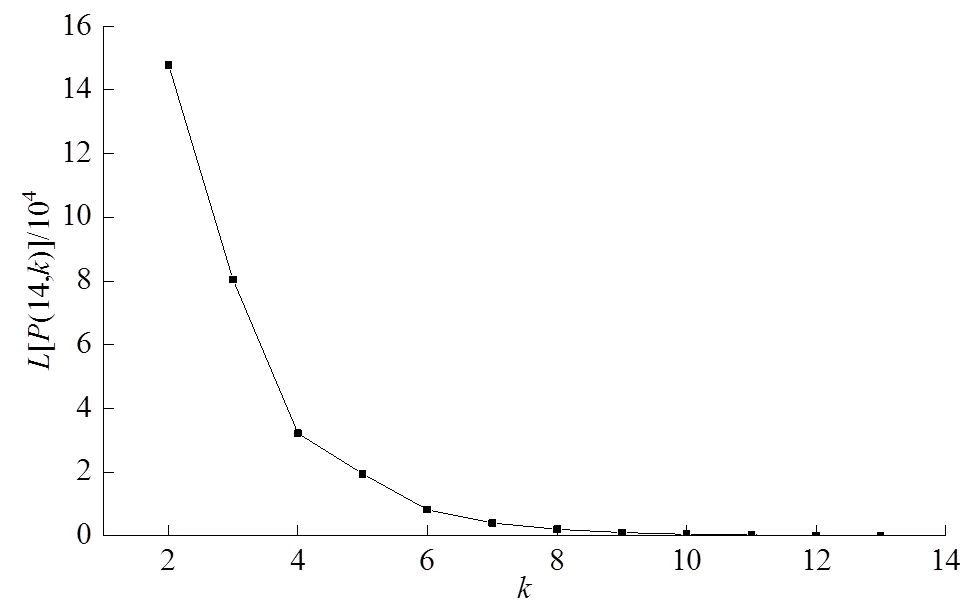
圖5 分類誤差曲線

根據2012－2015年的概率轉移矩陣和誤差狀態對2016年所屬狀態進行預測。由表1可知，2016年的相對誤差屬于2狀態，根據式（16）和式（17）計算得到修正值為57.70億m3，近似預測區間為(57.18, 58.24)。同理對其他年份進行預測，以此類推得到對應年份近似序列的修正值和預測區間，見表2。

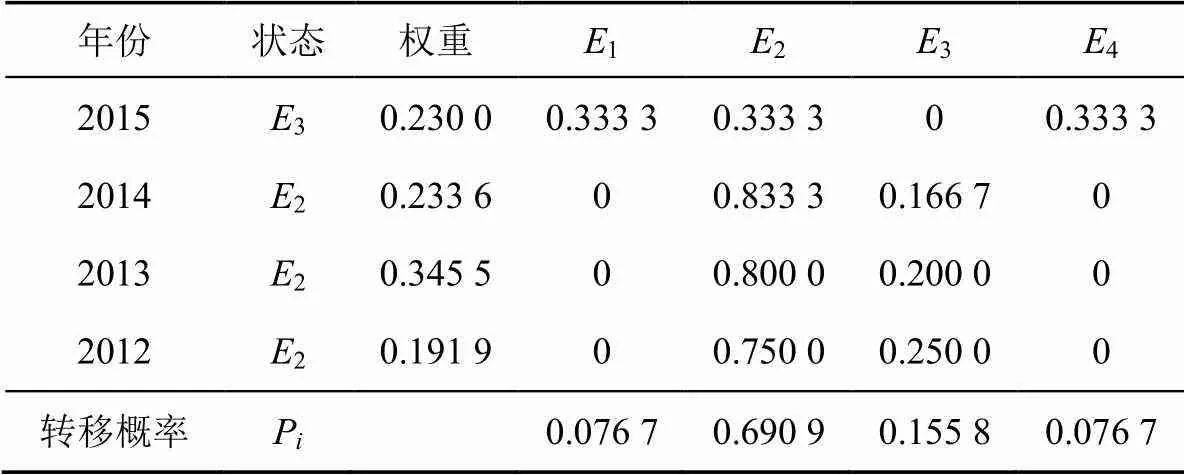
表1 2016年相對誤差狀態預測

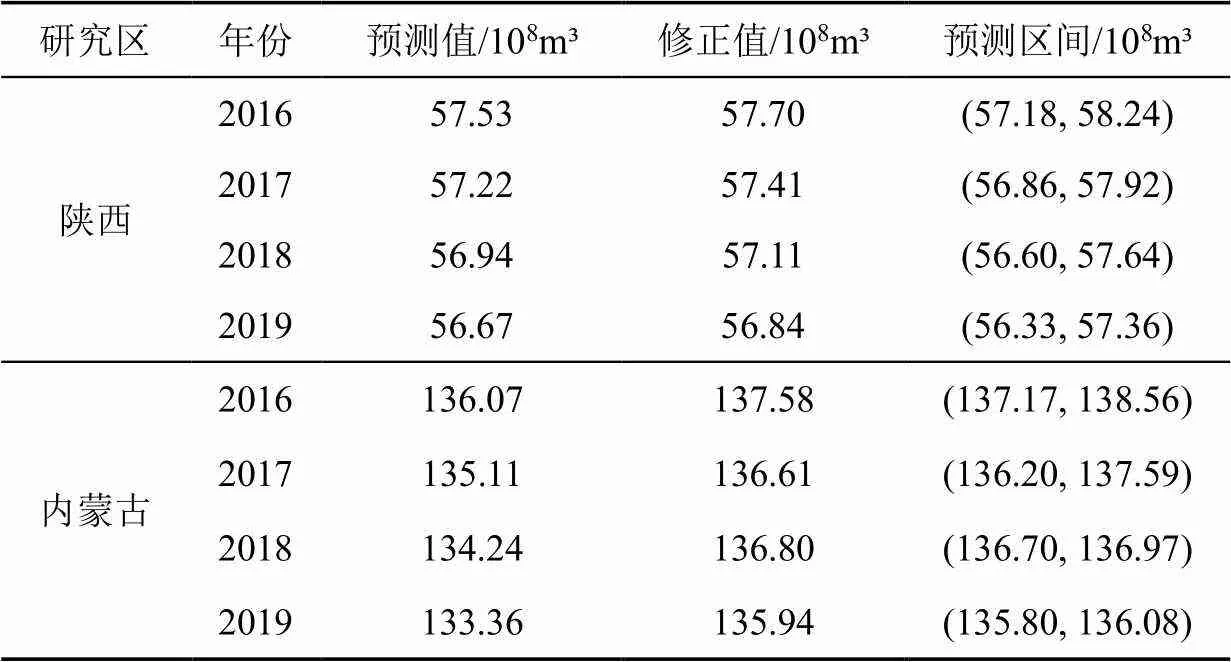
表2 加權馬爾可夫鏈修正結果

3.3 細節序列預測

利用SPSS軟件構建ARMA(,)模型對細節序列進行預測，依據AIC準則確定模型階數和，最終確定陜西省農業用水預測模型為ARMA(2,1)、ARMA(1,2)以及ARMA(2,2)，內蒙古農業用水預測模型為ARMA(2,1)、ARMA(2,1)以及ARMA(1,2)，擬合結果如圖6所示。

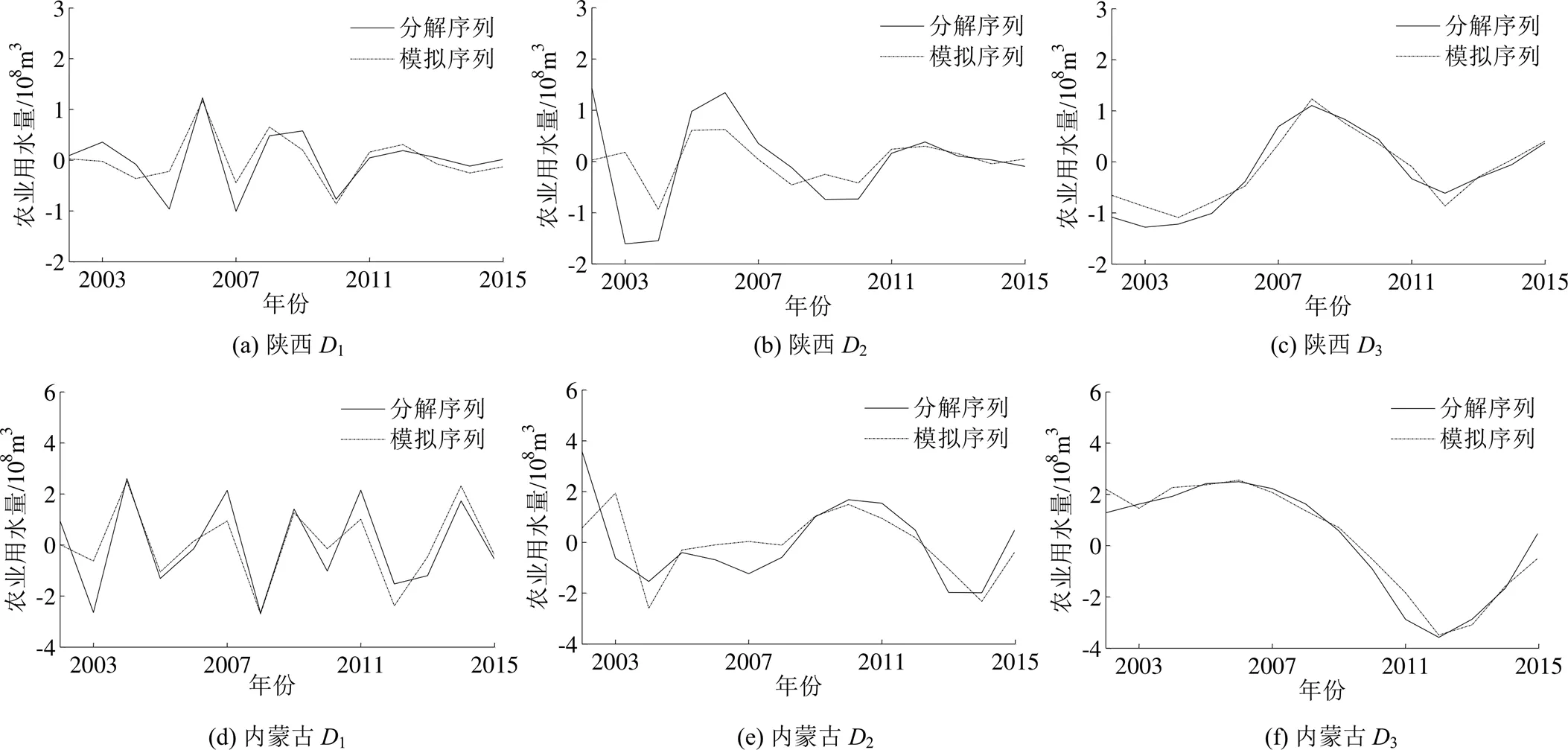
圖6 細節序列擬合結果

3.4 結果與分析

將近似序列和細節序列的預測結果疊加后得到農業用水量預測的最終結果，包括預測值和預測區間，如表3所示。從表3可以看出，2016—2018年陜西省農業用水量、2016—2017年內蒙古自治區農業用水量均在相應預測區間內，而2019年陜西省農業用水量和2018—2019年內蒙古自治區農業用水量未在預測區間內。這是由于加權馬爾可夫鏈在對未來誤差狀態區間進行預測時，會以驗證期中預測所得的非確定狀態為基礎狀態對未來狀態區間進行判斷，預測年限越長，基礎狀態中的不確定狀態越多，使得區間預測的不確定性隨著預測年限的增長而不斷增大，進而導致驗證期后期的區間預測失準。總的來說，加權馬爾可夫鏈能夠在短期（3 a）內對未來誤差狀態做出較為準確的判斷，并在修正農業用水量預測值的同時提供合理的預測區間。

為了進一步檢驗本文提出的DWT-WFGM(1,1)-ARMA模型的預測性能，以相同的原始數據為基礎，選擇GM(1,1)模型、DWT-GM(1,1)-ARMA模型、DWT-FGM(1,1)-ARMA模型以及DWT-WFGM(1,1)-ARMA模型進行對比分析。模型預測結果對比如圖7所示，預測性能對比結果如表4所示。

由圖7可知，相比其他模型，本文提出的DWT-WFGM(1,1)-ARMA模型能夠更好地擬合農業用水量的變化趨勢，具有更好的預測效果。

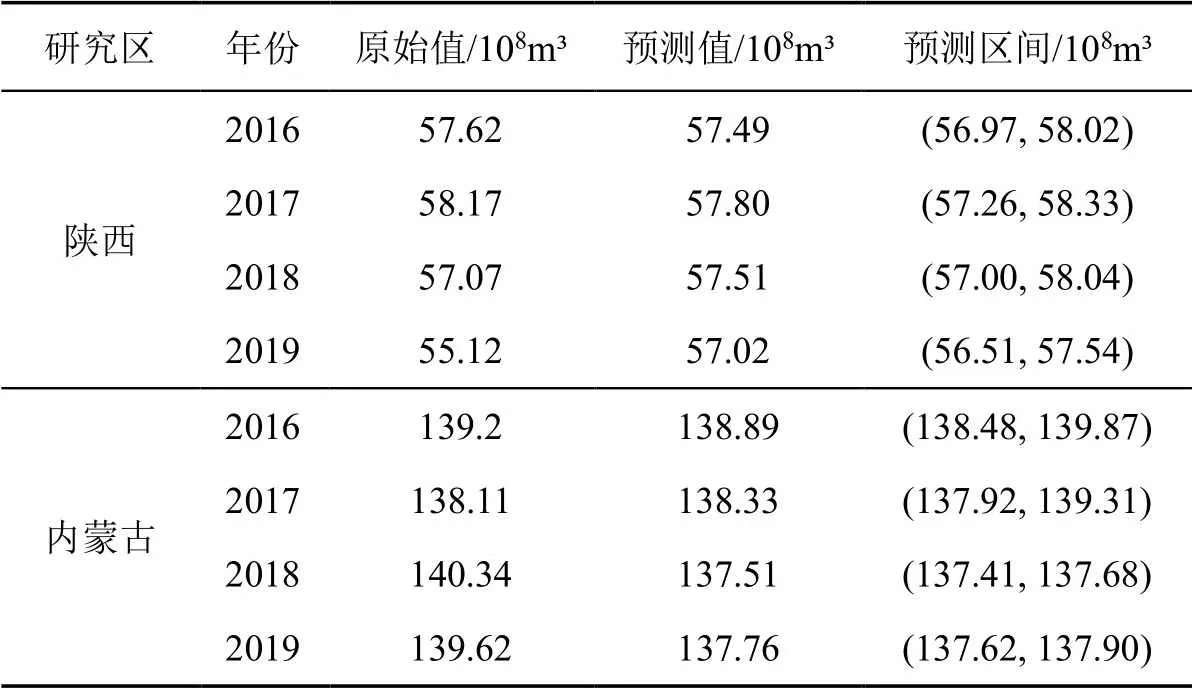
表3 農業用水預測區間

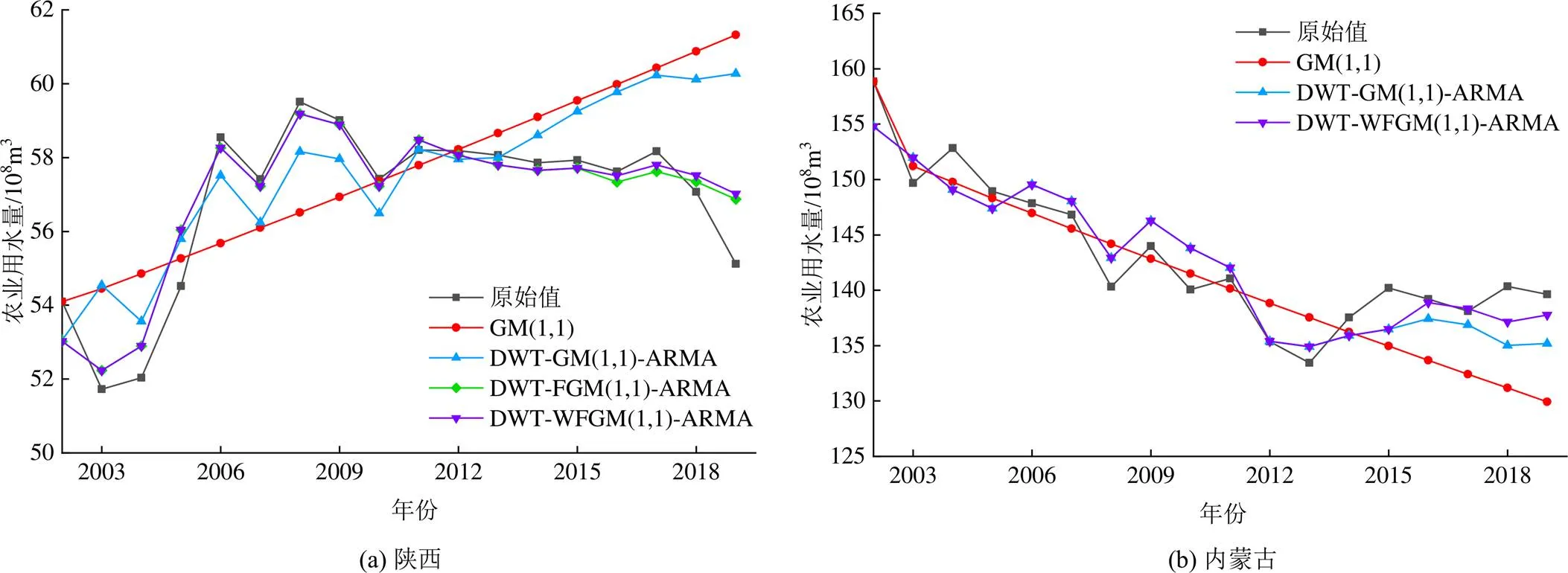
圖7 不同模型預測效果對比

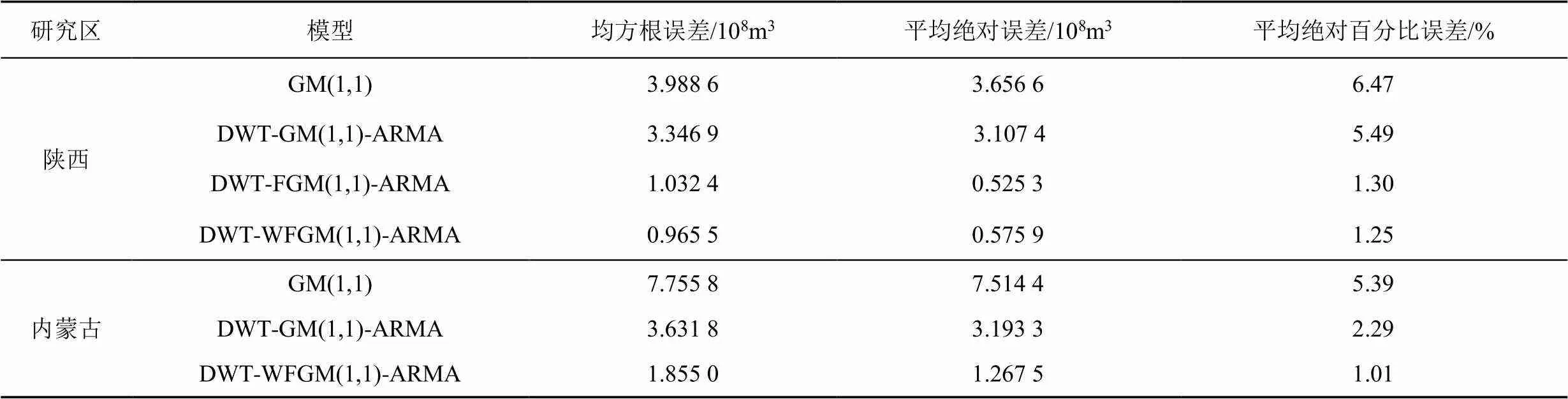
表4 預測結果精度評價

由表4可知，本文提出的DWT-WFGM(1,1)-ARMA模型的評價指標整體優于其他模型。相同條件下DWT-GM(1,1)-ARMA模型與GM(1,1)模型相比，評價指標、和在陜西省分別降低了14.9%、13.5%和13.7%，在內蒙古自治區分別降低了51.7%、58.8%和57.5%，這是由于離散小波變換處理可以降低原始序列的波動性，同時ARMA模型能夠對序列中的隨機成分進行有效的捕捉，在一定程度上提高了模型的預測精度。相同條件下DWT-FGM(1,1)-ARMA模型與DWT-GM(1,1)-ARMA模型相比，評價指標、和在陜西省分別降低了84.2%、84.8%和84.9%，在內蒙古自治區未發生變化（當=1時，FGM(1,1)模型轉化為GM(1,1)模型），說明FGM(1,1)模型能夠有效利用數據中的新信息，進一步優化模型的預測性能。相同條件下DWT-WFGM(1,1)-ARMA模型與DWT-FGM(1,1)-ARMA模型相比，評價指標在陜西省提高了9.5%，和分別降低了6.3%、3.9%，評價指標、和在內蒙古自治區分別降低了48.9%、60.3%和55.9%，說明加權馬爾可夫鏈能夠挖掘殘差序列中有價值的信息，并在短期內對序列誤差狀態區間做出較為準確的判斷。綜上所述，DWT-WFGM(1,1)-ARMA模型能夠解決傳統模型預測精度低、輸出結果單一的問題，對農業用水量預測具有良好的適用性。

4 討 論

本研究在DWT-GM(1,1)-ARMA模型的基礎上提出了新的農業用水量預測模型DWT-WFGM(1,1)-ARMA模型。經檢驗，新模型能夠在提高預測精度的同時為區域農業用水量提供合理的波動區間，主要原因是分數階灰色模型新信息利用的功能以及加權馬爾可夫鏈的修正作用。一方面，分數階灰色模型相較傳統灰色模型具有新信息優先、預測擾動小的優勢，在模擬預測中具有更高的精度，這與魏明奎等[22]的研究結果一致；另一方面，加權馬爾可夫鏈能夠對未來誤差狀態進行合理的預測，并在修正預測值的同時提供預測區間，蔣峰等[23]也證明了這一結論。

雖然新模型預測精度得到了較大改善，但本研究仍存在一些不足之處。首先，本研究選取的研究區數量較少，還需要在我國其他地區進行進一步的適用性研究。此外，除了本研究提出的區間預測方法外，以核密度估計法、分位數回歸法等為基礎的區間預測方法被廣泛應用于風電功率、光伏出力預測等領域[24-25]，而較少應用于農業用水預測領域，農業用水的區間預測有待進一步深入研究。

5 結 論

1）DWT-FGM(1,1)-ARMA組合模型能夠有效消除原始用水序列的波動性，且分數階灰色模型FGM(1,1)和ARMA模型相結合，在充分利用序列的新信息同時提高了模型對于序列隨機成分的捕捉能力，能夠有效提高模型的預測效果。

2）DWT-WFGM(1,1)-ARMA組合模型采用加權馬爾可夫鏈對DWT-FGM(1,1)-ARMA模型預測結果進行修正，能夠進一步利用殘差數據中的有效信息，提高模型的預測性能。且相較傳統預測模型可以在短期內同時對未來農業用水量和用水區間進行有效預測，為區域農業用水預測工作提供新的思路。

3）在采用加權馬爾可夫鏈對誤差狀態區間進行預測的過程中，誤差狀態預測的不確定性隨著預測年限的增長不斷增大，進而導致長期預測的結果失準。經檢驗，加權馬爾可夫鏈在短期（3 a）內修正預測的準確率較高，可以為短期農業用水量預測提供更加可靠的依據。

4）在歷史樣本較小的條件下，應用DWT-WFGM(1,1)-ARMA組合模型對陜西省和內蒙古自治區農業用水量預測的平均絕對百分比誤差分別為1.25%和1.01%，相比其他模型預測精度最高，是一種有效的農業用水預測方法。

[1] 李保國, 黃峰. 1998—2007年中國農業用水分析[J]. 水科學進展, 2010, 21(4): 575-583.

LI Baoguo, HUANG Feng. Trends in China’s agricultural water use during recent decade using the green and blue water approach[J]. Advances in Water Science, 2010, 21(4): 575-583.

[2] 崔丙健, 高峰, 胡超, 等. 非常規水資源農業利用現狀及研究進展[J]. 灌溉排水學報, 2019, 38(7): 60-68.

CUI Bingjian, GAO Feng, HU Chao, et al. The use of brackish and reclaimed waste water in agriculture: a review[J]. Journal of Irrigation and Drainage, 2019, 38(7): 60-68.

[3] 趙桂生, 張海文, 劉愛軍, 等.基于等維遞補灰色GM(1,1)模型的我國農業灌溉用水預測分析[J]. 數學的實踐與認識, 2018, 48(4): 299-304.

ZHAO Guisheng, ZHANG Haiwen, LIU Aijun, et al. Prediction and analysis of agricultural irrigation water in China based on grey GM (1, 1) model with equal dimension[J]. Mathematics in Practice and Theory, 2018, 48(4): 299-304.

[4] 黃修橋, 康紹忠, 王景雷. 灌溉用水需求預測方法初步研究[J]. 灌溉排水學報, 2004, 23(4): 11-15.

HUANG Xiuqiao, KANG Shaozhong, WANG Jinglei. A preliminary study on predicting method for the demand of irrigation water resource [J]. Journal of Irrigation and Drainage, 2004, 23(4): 11-15.

[5] 劉迪, 胡彩虹, 吳澤寧. 基于定額定量分析的農業用水需求預測研究[J]. 灌溉排水學報, 2008, 27(6): 88-91.

LIU Di, HU Caihong, WU Zening. Predicting method for demand of agriculture water based on quantitative analysis[J]. Journal of Irrigation and Drainage, 2008, 27(6): 88-91.

[6] 白鵬, 龍秋波. 3種用水量預測方法在京津冀地區的適用性比較[J]. 水資源保護, 2021, 37(2): 102-107.

BAI Peng, LONG Qiubo. Applicability comparison of three water consumption prediction methods in Beijing-Tianjin-Hebei region[J]. Water Resources Protection, 2021, 37(2): 102-107.

[7] ZHANG X Q, YUE M L, YAO Y, et al. Regional annual water consumption forecast model[J]. Desalination and Water Treatment, 2018, 114: 51-60.

[8] LIU S F, TAO L Y, XIE N M, et al. On the new model system and framework of grey system theory[J]. Journal of Grey System, 2016, 28(1): 1-15.

[9] 崔東文, 包艷飛. 基于人工生態系統優化算法的組合生長需水預測模型[J]. 水資源保護, 2020, 36(6): 122-130.

CUI Dongwen, BAO Yanfei. Combined growth water demand forecasting model based on artificial ecosystem optimization algorithm[J]. Water Resources Protection, 2020, 36(6): 122-130.

[10] 佟長福, 史海濱, 包小慶, 等. 基于小波分析理論組合模型的農業需水量預測[J]. 農業工程學報, 2011, 27(5): 93-98.

TONG Changfu, SHI Haibin, BAO Xiaoqing, et al. Application of a combined model based on wavelet analysis for predicting crop water requirement[J]. Transactions of the Chinese Society of Agricultural Engineering, 2011, 27(5): 93-98.

[11] 鄧權龍, 蔣仲安, 韓碩. 基于小波分析與GM(1,1)-ARMA(p,q)組合的礦井防塵用水量預測[J]. 礦業安全與環保, 2018, 45(4): 75-79.

DENG Quanlong, JIANG Zhongan, HAN Shuo. Prediction of coal mine dustproof water consumption based on the combination of wavelet analysis and GM (1, 1)-ARMA (p, q)[J]. Mining Safety & Environmental Protection, 2018, 45(4): 75-79.

[12] TIWARI M K, ADAMOWSKI J F. Medium-term urban water demand forecasting with limited data using an ensemble wavelet–bootstrap machine-learning approach[J]. Journal of Water Resources Planning and Management, 2015, 141(2): 04 014 053.

[13] 吳利豐, 劉思峰, 劉健. 灰色GM(1,1)分數階累積模型及其穩定性[J]. 控制與決策, 2014, 29(5): 919-924.

WU Lifeng, LIU Sifeng, LIU Jian. GM(1,1) model based on fractional order accumulating method and its Stability[J]. Control and Decision, 2014, 29(5): 919-924.

[14] 王俊芳, 羅黨. 振蕩序列的分數階離散GM(1,1)冪模型及其應用[J]. 控制與決策, 2017, 32(1): 176-180.

WANG Junfang, LUO Dang. Fractional order discrete grey GM(1,1) power model based on oscillation sequences and its application[J]. Control and Decision, 2017, 32(1): 176-180.

[15] 潘顯俊, 張煒, 趙田, 等. 分數階離散灰色模型及其在備件需求預測中的應用[J]. 兵工學報, 2017, 38(4): 785-792.

PAN Xianjun, ZHANG Wei, ZHAO Tian, et al. Fractional order discrete grey model and its application in spare parts demand forecasting[J]. Acta Armamentarii, 2017, 38(4): 785-792.

[16] MA X, MEI X, WU W Q, et al. A novel fractional time delayed grey model with Grey Wolf Optimizer and its applications in forecasting the natural gas and coal consumption in Chongqing China[J]. Energy, 2019, 178: 487-507.

[17] WU L, LI N, ZHAO T. Using the seasonal FGM(1, 1) model to predict the air quality indicators in Xingtai and Handan[J]. Environmental Science and Pollution Research, 2019, 26(14): 14 683-14 688.

[18] 郝麗娜, 粟曉玲, 黃巧玲. 基于小波廣義回歸神經網絡耦合模型的月徑流預測[J]. 水力發電學報, 2016, 35(5): 47-54.

HAO Lina, SU Xiaoling, HUANG Qiaoling. Monthly runoff prediction using wavelet transform and generalized regression neural network model[J]. Journal of Hydroelectric Engineering, 2016, 35(5): 47-54.

[19] 趙建忠, 徐廷學, 葛先軍, 等. 基于小波變換和GM-ARMA的導彈備件消耗預測[J]. 北京航空航天大學學報, 2013, 39(4): 553-558.

ZHAO Jianzhong, XU Tingxue, GE Xianjun, et al. Consumption forecasting of missile spare parts based on wavelet transform and revised GM-ARMA model[J]. Journal of Beijing University of Aeronautics and Astronautics, 2013, 39(4): 553-558.

[20] LI F, LIU S F, YAO L G, et al. Grey system model with the fractional order accumulation [J]. Communications in Nonlinear Science and Numerical Simulation, 2013, 18(7): 1 775-1 785.

[21] 季玉琦, 耿光飛, 溫渤嬰, 等. 基于最優分割法的含DG配電網動態無功優化[J]. 電網技術, 2017, 41(8): 2 585-2 592.

JI Yuqi, GENG Guangfei, WEN Boying, et al. Dynamic reactive power optimization in distribution network with DG based on optimal partition[J]. Power System Technology, 2017, 41(8): 2 585-2 592.

[22] 魏明奎, 周全, 蔡紹榮, 等. 基于BFGS-FA優化的分數階灰色模型的中長期負荷預測[J]. 廣西大學學報(自然科學版), 2020, 45(2): 270-276．

WEI Mingkui, ZHOU Quan, CAI Shaorong, et al. Mid-Long term Load forecasting based on fractional gray model optimized by BFGS-FA[J]. Journal of Guangxi University (Natural Science Edition), 2020, 45(2): 270-276.

[23] 蔣峰, 王宗耀, 張鵬. 基于灰色-加權馬爾可夫鏈的光伏發電量預測[J]. 電力系統保護與控制, 2019, 47(15): 55-60.

JIANG Feng, WANG Zongyao, ZHANG Peng. Forecasting power generation of solar photovoltaic system based on the combination of grey model and weighted Markov chain[J]. Power System Protection and Control, 2019, 47(15): 55-60.

[24] 賴昌偉, 黎靜華, 陳博, 等. 光伏發電出力預測技術研究綜述[J]. 電工技術學報, 2019, 34(6): 1 201-1 217.

LAI Changwei, LI Jinghua, CHEN Bo, et al. Review of photovoltaic power output prediction technology[J]. Transactions of China Electrotechnical Society, 2019, 34(6): 1 201-1 217.

[25] 楊茂, 董昊. 基于數值天氣預報風速和蒙特卡洛法的短期風電功率區間預測[J]. 電力系統自動化, 2021, 45(5): 79-85.

YANG Mao, DONG Hao. Short-term wind power interval prediction based on wind speed of numerical weather prediction and Monte Carlo method[J]. Automation of Electric Power Systems, 2021, 45(5): 79-85.

Predicting Agricultural Water Demand Using the DWT-WFGM (1,1)-ARMA Model

WANG Guanzhi1,2, SU Xiaoling1,2*, ZHANG Te1,2, JIANG Tianliang1,2, CHU Jiangdong1,2

(1.College of Water Resources and Architectural Engineering, Northwest A&F University, Yangling 712100, China; 2. Key Laboratory of Agricultural Soil and Water Engineering in Arid Area of Ministry of Education, Northwest A&F University, Yangling 712100, China)

【】The increased demand for water due to economic development coupled with dwindling water supply is the double whammy facing most provinces in north China. Given agriculture is the biggest water use sector, understanding the change in agricultural water demand is critical to improving water resources management. The purpose of this paper is to present a new method to estimate agricultural water use changes at provincial scale in the north of China.【】The proposed method was based on discrete wavelet transform (DWT), fractional-order grey model (FGM(1,1)), weighted Markov Chain (WMC), and autoregressive moving average (ARMA) model. The time series of agricultural water demand was firstly decomposed into approximate series and detailed series, respectively, using DWT. FGM(1,1) was then used to describe the approximate series, with the errors corrected by WMC. The Fisher optimal segmentation method was used to divide the state intervals of the predicted errors, and the state intervals were predicted using a probability transfer matrix. The predicted intervals and values of the approximate series were obtained from the boundary values and median of the predicted error state intervals. In comparison, the detailed series were predicted using the ARMA model based on the Akaike Information Criteria. These were used to predict the agricultural water demand and its intervals. We applied the models to agricultural water demand in Shaanxi and Inner Mongolia provinces, with data measured from 2002 to 2015 used to train the model and those measured from 2016 to 2019 to validate the model. We compared the results calculated from the proposed model with those estimated from the traditional GM (1,1), DWT- GM(1,1)-ARMA, and DWT-FGM(1,1)-ARMA models.【】The average absolute error of the proposed model for the two provinces was 1.25% and 1.01%, respectively, much less than those given rise to by other models. The predicted agricultural water demand intervals showed that after correction by WMC, the model provided reliable short-term fluctuation intervals in agricultural water demand in both provinces.【】The proposed model for predicting agricultural water demand at provincial scale was accurate and robust. It can also predict the intervals which describe the short-term fluctuation in agricultural water demand. The model has an implication in helping improve water management and developing sustainable agriculture.

agricultural water consumption; fractional-order grey model; weighted Markov chains; discrete wavelet transform; predicted intervals

TV213.4

A

10.13522/j.cnki.ggps.2021177

王冠智, 粟曉玲, 張特, 等. 基于DWT-WFGM(1,1)-ARMA組合模型的農業用水量預測[J]. 灌溉排水學報, 2021, 40(11): 106-114.

WANG Guanzhi, SU Xiaoling, ZHANG Te, et al. Predicting Agricultural Water Demand Using the DWT-WFGM (1,1)-ARMA Model[J]. Journal of Irrigation and Drainage, 2021, 40(11): 106-114.

1672 - 3317（2021）11 - 0106 - 09

2021-04-28

國家自然科學基金項目（52079111）；“十三五”國家重點研發計劃項目（2016YFC0401306）

王冠智（1997-），男，山東日照人。碩士研究生，主要從事用水預測研究。E-mail: guanzhiwang@163.com

粟曉玲（1968-），女，四川開江人。教授，博士生導師，主要從事水文模擬及水資源優化研究。E-mail: xiaolingsu@nwafu.edu.cn

責任編輯：陸紅飛