基于FCM的地震波形聚類方法研究

朱乾菲，柴變芳，韓 紅，碩良勛

ZHU Qian-feia, CHAI Bian-fangb, HAN Hongb, SHUO Liang-xunb

河北地質大學 a.地球科學學院，b.信息工程學院，河北 石家莊 050031

Hebei GEO University, Shijiazhuang 050031, China

0 引言

原始地震記錄中包含了大量的地下介質的響應信息，而地震記錄與儲層有著極其復雜的非線性關系[1]，要想在兩者之間直接建立具有量化的關系非常有難度。為了使用地震數據來表征儲層非均質性，通常引入地震相分析技術來生成描述儲層范圍并識別其地質特征的地圖[2-3]。波形分類是地震相分析中常用的一種儲層預測技術波形分類技術是解決地震相問題和儲層預測的重要方法[4]。地震波形具有直觀的解釋意義[5]，地震波形變化及其分布規律是重要的地震參數之一[6]。沿解釋層位提取的波形帶有振幅、頻率和相位信息。因此，波形分類技術已被證明是地震相分析的有力方法[7-9]。

地震波形分類屬性的分析方法最早于1982年由Naaman Keskes等提出, 并應用于二維地震測網的追蹤研究[10]。1984年, Sibille[11]較為系統地提出了波形聚類分析基本原理, 即根據地震反射界面中同相軸排列組合的多種屬性（雜亂、波狀、平行和復合波形）,采用多元統計方法進行歸類, 并將其初步用于地震相分析研究。1990年，Kohonen提出自組織神經網絡（SOM）；2003年，Saggaf等人[12]提出了一種競爭神經網絡來分類波形，用于無監督地震相分類和儲層相的自動識別；2012年，Priezzhev I等[13]提出了應用基于K平均值和SOM的三維波形地震相分類方法；2014年，Chopra和Marfurt[14]使用生成地形圖進行地震波形分類。由于地質結構普遍復雜與多樣性，某些不同地質體過渡范圍反射的波形通常應該是以一定的模糊值屬于各個波形模式類別，而不應以一個確定值屬于一個類。本文引入模糊C均值聚類（FCM）對地震相進行分類，可以使不同相之間的界限變得平滑。采用FCM的結果會讓地震相變得更好解釋，即地質結構展示的更豐富，為相關地質解釋人員提供更多的參考依據。

1 基于FCM的地震波形聚類算法

1.1 FCM介紹

模糊C均值聚類算法（ Fuzzy C-Means algorithm）也稱FCM。FCM算法在聚類算法中應用最廣泛且較成功。本質是利用每個樣本點對所有類中心的隸屬度來優化目標函數，以此決定樣本點的類屬以達到自動對樣本數據進行分類的目的。

1.1.1 隸屬度函數的概念

隸屬度函數是表示數據集中任何一個元素對象x屬于該集合A程度，其自變量范圍是A中任一對象，取值范圍為[0,1]，即0≦μA(x)≦1。即為定義了一個在空間X={x}上的隸屬度函數就等同于定義了一個模糊集合A可以表示為：

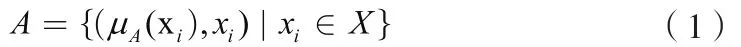
1.1.2 模糊C均值聚類FCM

模糊C均值聚類（FCM），是利用隸屬度函數來確定樣本點屬于某個類的程度的一種算法。假設樣本集合為D={x1,x2,…,xn}代表的是n個樣本的特征向量集，對于D進行模糊聚類得到c個簇C1,C2,…,Cc,P=(P1,P2,…,Pc)代表所有子集的聚類中心集合，其中U=（uij）代表隸屬度矩陣，隸屬度uij是用來表明樣本Xi與其子集Cj的隸屬關系，應該滿足：

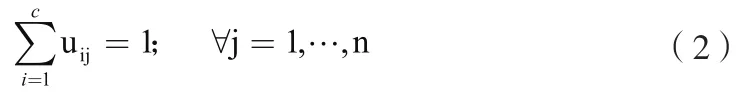
FCM聚類算法進行模糊聚類，它的非相似性指標的目標函數可以定義為：

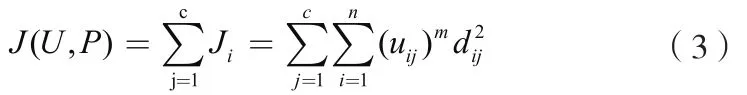
其中，J代表實例數據和聚類中心的距離平方和；dij代表的第i個數據點與第j個聚類中心是一種距離度量函數，聚類中心分布狀況不同，所選擇的函數種類也許不同，一般采用歐式距離。

構造如下新的目標函數，使式（3）達到最小值的必要條件：

這里λj，j=1到n，是式（2）的n個約束式的拉格朗日乘子。m：用來決定隸屬度矩陣U模糊水平的系數，通常也叫做平滑因子，U的模糊水平與m值呈正相關。對所有輸入參量求導，使式（4）達到最小的必要條件為：

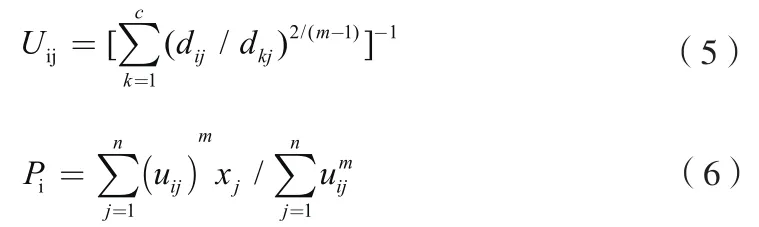
迭代過程中聚類中心和隸屬度是持續調整的，一直到符合迭代條件。FCM聚類算法的隸屬度沒有硬性規定屬于1或0，而是能夠在不同類別之間模糊取值。由這兩個必要條件，FCM算法可以理解為一個簡單的迭代過程[15]。

1.2 基于FCM的地震波聚類算法

FCM算法是一種無監督學習方法，可以識別多維空間中的數據點組或聚類。波形分類利用FCM算法，首先將波形樣本集分為C類找到每類的聚類中心，根據每一道波的隸屬度進行劃分，將所有道波劃分為最佳類別，形成地震相。詳細描述如表1所示。

表1 基于FCM的地震波聚類算法Table 1 Seismic wave clustering algorithm based on FCM

2 算法測試

首先利用人工合成的地震數據驗證FCM算法在波形分類中的有效性，然后利用實際工區的地震數據實現基于FCM的地震波形聚類。

2.1 合成地震數據的測試

由于獲取標注地震波數據較難，下面通過正演模型構造人工地震波數據。假設人工模型的相關數據如圖1所示。（模型中每一層的厚度為500 m，采樣率：0.001 s）

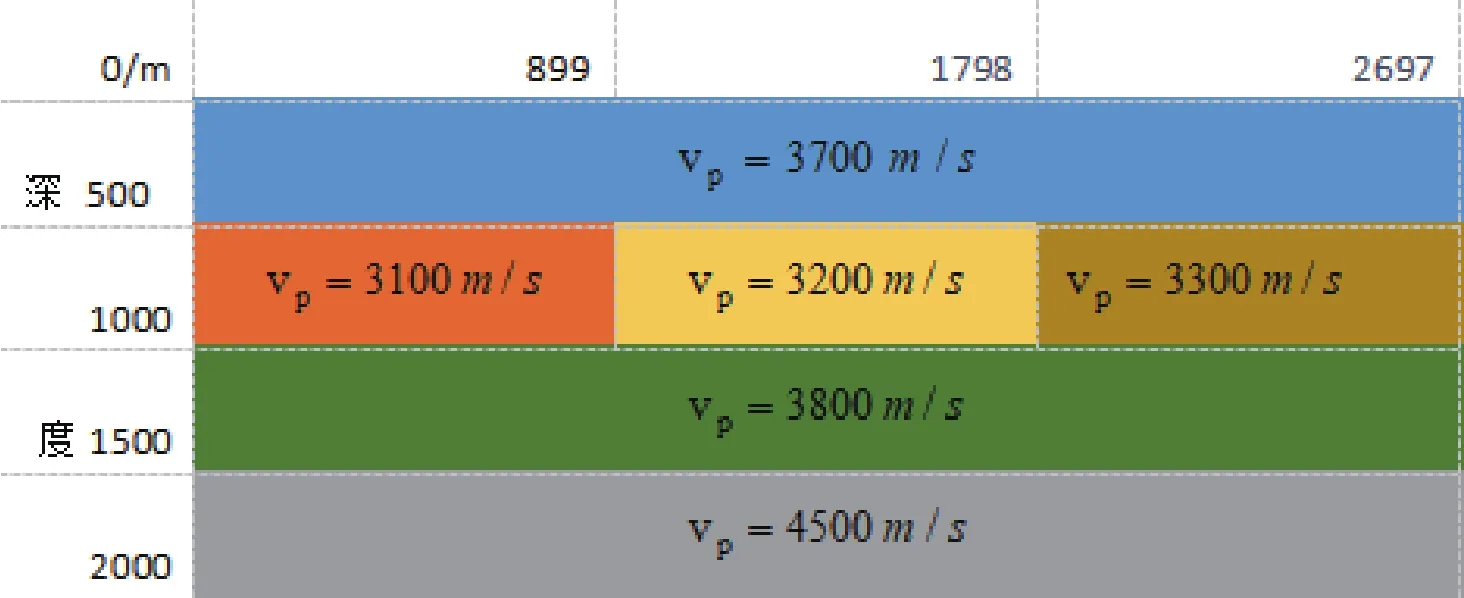
圖1 人工模型的速度數據信息Fig.1 Velocity data information of artificial model

圖1中可以看出在深度500～1 000 m時，可以看到該數據有三大類的地震數據，地震波的速度分別為：vp=3 100 m/s、vp=3 200 m/s、vp=3 300 m/s。檢波器間隔設為3 m，所以總共生成900道波。圖2可以看出解析層位取常數0.6 s處，層位上下各取0.1 s，得到的地震波形每道200個點。

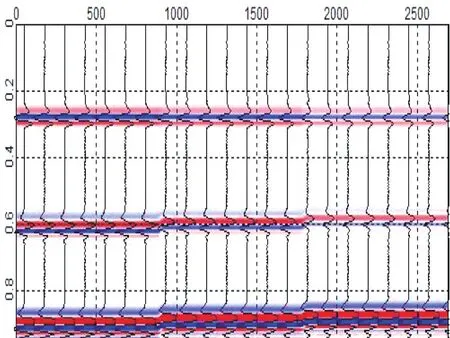
圖2 正演合成記錄Fig.2 Forward synthetic record

圖3可以看出，利用FCM算法將900道地震波分為了3類，每類含有的地震波約為300道，與合成地震數據的參數相符合。

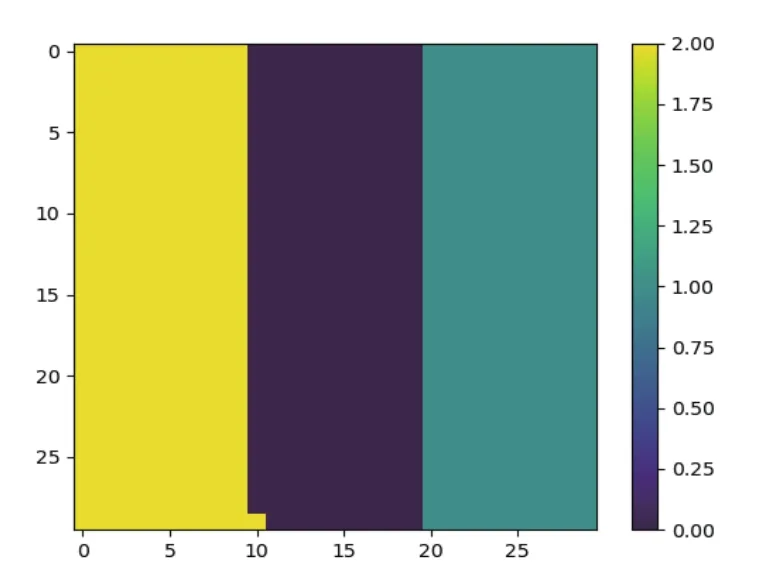
圖3 FCM聚類結果Fig.3 FCM clustering results

2.2 工區地震數據測試

2.2.1 工區數據介紹

本文用到的數據是dGB地球科學公司的荷蘭北海F3的疊后地震解釋數據集，該數據集包含384 km2的地震數據，共有951條inline，651條Xline，采樣率是4 ms，記錄1 848 ms,生成了9個不同的層位，現作為地質方面的一個公開的數據體[17]。選取了F3工區的其中一個層位作為分析層位，該區域的時間切片如圖4；層位顯示如圖5.沿著該層位上取20 ms和下取20 ms作為分析的數據范圍，Xline號：304—1246，Inline號：104—696。

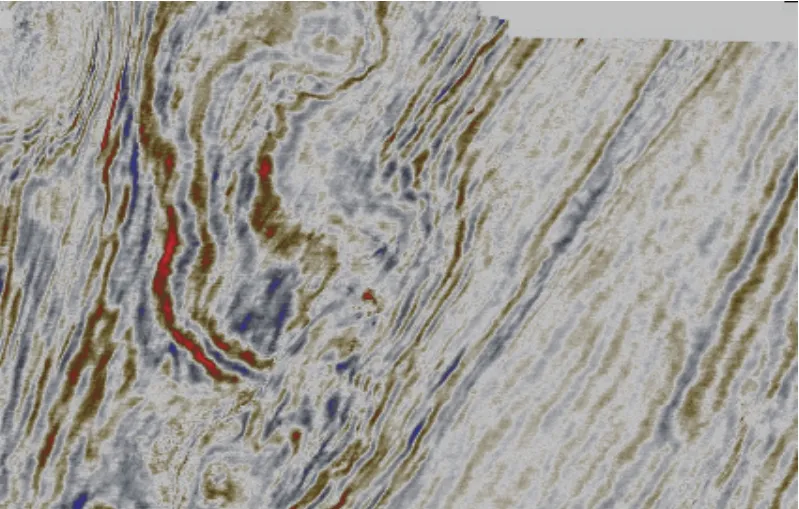
圖4 工區 928 ms切片圖Fig.4 928 ms section map of work area

圖5 工區層位圖Fig.5 Horizon map of work area

2.2.2 算法應用

FCM屬于劃分聚類方法，是K均值算法在模糊數學和可能性理論下的自然擴展。所以本文也使用了K均值算法對地震波形進行聚類，與FCM算法形成對比。因為K均值算法中的K值不好確定，所以使用肘部法則確定K值。

應用肘部法則確定K-means聚類算法的最佳K值為10，結果如圖6。分別使用K均值方法和FCM算法對研究區域數據處理，處理結果如圖7和圖8。

圖6 肘部法則確定K值Fig.6 Determination of K value by elbow rule

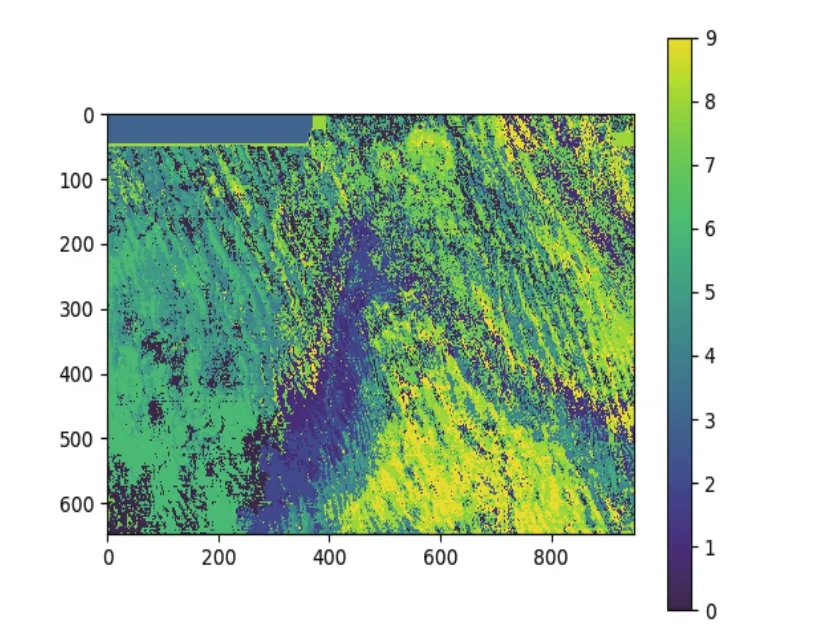
圖7 基于K均值聚類結果（運行時間：78.069 s）Fig.7 Clustering results based on K-means

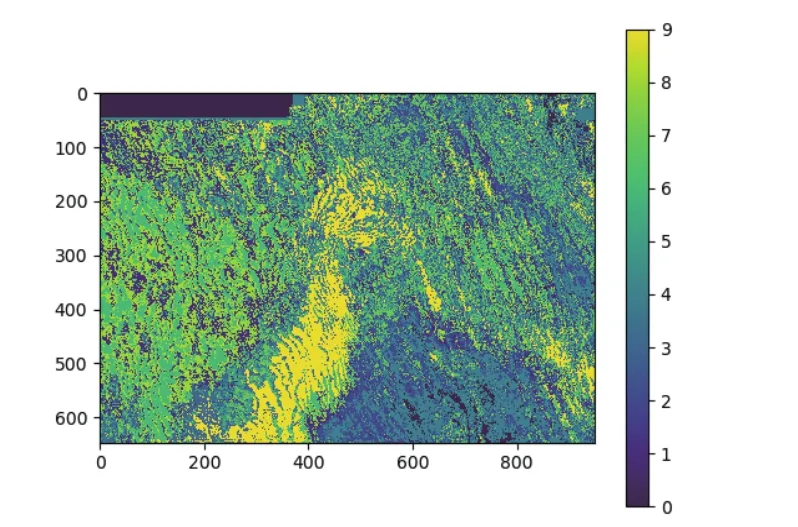
圖8 基于FCM聚類結果（運行時間：89.506 s）Fig.8 Clustering results based on FCM

實驗工區所選波形數據是647×949總共614 003個波形數據，基于FCM算法分為了10類。在這個10類波形數據中，選出來每一類波形中隸屬度最大的一條波如表2所示，每條波都會有十個隸屬度值，最大隸屬度值則對應其類別。同時畫出所選數據中數據522 522和511 682，從圖9中可以看出波形相似，但是因為隸屬度不同，所謂將其分為了兩類。

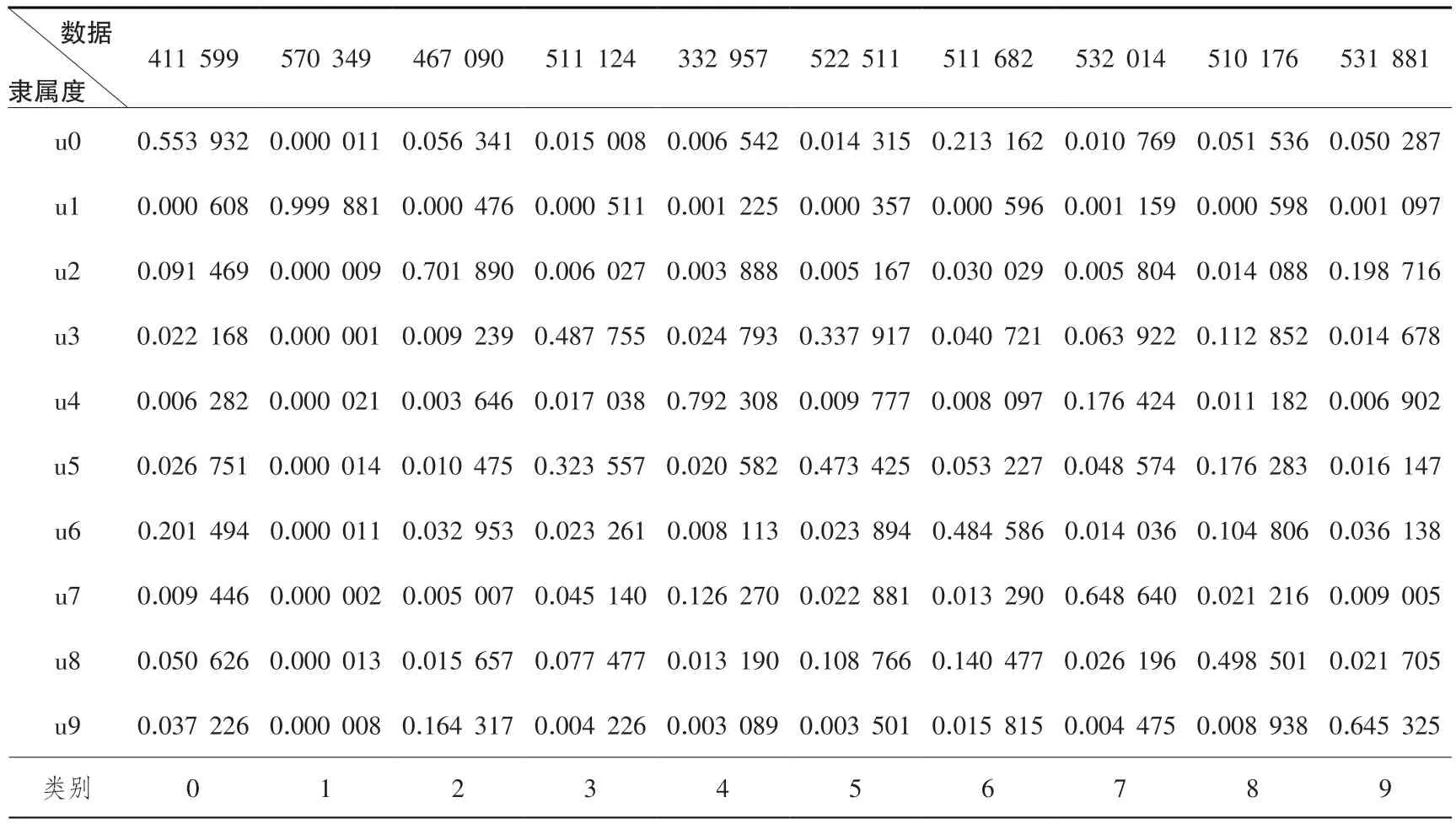
表2 數據隸屬度Table 2 Data membership degree

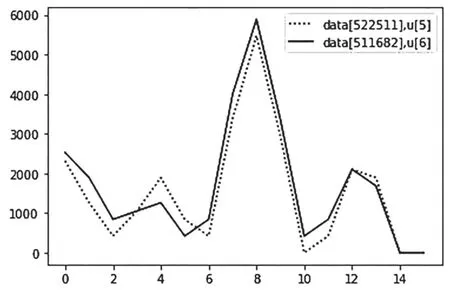
圖9 數據波形圖Fig.9 Data waveform diagram

2.3 實驗小結

FCM聚類算法在人工合成數據中的應用，證明了基于FCM的地震波聚類方法的有效性。同時通過FCM和K均值兩種聚類方法在荷蘭F3工區數據進行波形分類可以得到以下結論：

1.FCM聚類算法是在K均值算法的基礎上進行發展，可以對缺少先驗知識的對象進行分類，通過人腦思維信息，使分類結果更符合客觀實際,可以給出相對的最優分類結果，因此具有一定的實用性。然而該算法也有一些缺點，主要有：聚類結果取決與參數的初始化選取，這些參數的設定，會影響聚類結果的正確性。

2.速度比較：從上述兩種聚類結果分析中可得，FCM聚類代碼運行時間和K均值聚類代碼運行時間分別為89.506 s和78.069 s。因為FCM聚類比K均值聚類的迭代次數更多，從而計算量更大，以至于數據處理的更加細膩，所以速度會慢一些。

3.FCM算法在分類結果上根據每個數據的隸屬度進行劃分，即使數據不完全相似，但是所屬隸屬度相同也可以劃分為一類；反之，數據波形可能相似，隸屬度不同也可能被分為不同類別。所以FCM算法更加精細，由該方法獲得地震相的種類刻畫的更加細致，為相應地質解釋人員對沉積相的解釋提供了更加可靠的參考依據。

3 結論

本文提出了一種用于波形分類的模糊C均值算法。此方法使用模糊值來計算波形之間的相似性。將此算法應用于人工合成數據和實際工區數據，并在實際工區數據中使用K均值算法和FCM算法得到的結果進行比較，發現不同的地質特征在FCM產生的分類結果中容易區分，而從傳統的K均值算法得到的結果是較差的。

雖然波形分類方法在地震相分析方面已經取得了一定的成果，但是想要得到突破，還需要進一步探索。在接下來的研究工作中，會繼續學習利用其他算法使波形分類效果更好。