重力梯度力矩作用下近地衛星自旋運動規律分析

蔡立鋒，張國云，洪濤，李衛平，林海晨，孫振江

中國西安衛星測控中心 宇航動力學國家重點實驗室，西安 710043

1 引言

近地衛星一般處于主動姿態控制下三軸穩定運動狀態，衛星在軌常發生姿態失控故障，此時常處于無主動控制情況下的自旋狀態，對于其自旋姿態的確定和預測是姿態故障恢復的前提[1-4]。當衛星到達壽命末期，由于部件故障等原因需要對衛星進行離軌或鈍化，使得衛星處于姿態無控狀態，可以設計近地衛星姿態自旋策略，使衛星仍然保持能源供應和測控。比如對某近地衛星離軌處置后的姿態自旋策略，提出了一種長期在軌穩定自旋的姿態控制模式[5]。因此，很有必要對近地衛星自旋運動規律作進一步研究。

近地衛星受地球扁率J2項攝動，軌道面一般處于進動狀態。典型的太陽同步軌道衛星，軌道面隨太陽進動，同時受到重力梯度、太陽光壓、地磁、氣動等復雜攝動力矩作用，使得星體角動量在慣性空間指向發生變化。一般來說，對于低軌衛星，重力梯度和地磁力矩起主要作用[6]。地磁力矩來源于星上電子儀器產生的剩余磁場，或者來自姿態控制用的磁矩線圈，均與衛星星上狀態有關。本文主要考慮重力梯度力矩作用下衛星運動規律。

受地球重力梯度力矩作用下的自旋衛星的運動規律，從自旋衛星的平衡狀態角度，有著名的湯姆孫(Thomson)平衡和萊金斯-普林格爾(Likins-Pringle)平衡[7-9]。其中湯姆孫平衡自旋軸指向軌道面法線；萊金斯-普林格爾平衡要求自旋軸進動角速率等于軌道角速度，自旋角速率一般小于軌道角速度。這幾種自旋平衡條件是在假設衛星為軸對稱剛體，并且衛星軌道為圓形且軌道面不存在進動，實際上除了傾角為90°以外的低軌衛星軌道面均存在進動。文獻[10]分析了重力梯度作用下軸對稱飛行器自旋運動，給出了進動角速率近似解。當衛星自旋角速率較大時，文獻[11-12]指出對于受微弱力矩作用的高速旋轉剛體，應用Serert-Andoyer正則變量可使分析過程明顯簡化。文獻[13-16]運用基于Serert-Andoyer正則變量分析了自旋運動及重力梯度作用下的近似解。文獻[17]利用數值仿真的方法研究了重力梯度力矩引起的自旋穩定衛星姿態攝動，發現一些運動規律，但仍沒有考慮存在軌道攝動的情況。本文建立非軸對稱近地衛星在受地球非球形等攝動軌道面緩慢進動時，在重力梯度影響下的姿態運動模型，推導自旋角速率滿足一定條件下自旋運動的進動角、章動角、自旋角的解析解，討論近地衛星自旋姿態在重力梯度攝動下運動規律及其應用價值。

2 姿態攝動常微分方程組

2.1 姿態運動方程

定義衛星軌道坐標系，z軸由衛星質心指向地心，x軸在軌道平面內與z軸垂直，指向衛星運動的方向，y軸與z、x軸成右手螺旋關系。定義交點軌道系為衛星處于升交點時的軌道坐標系。星體相對于交點軌道系的姿態采用歐拉角，為便于分析自旋軸進動規律，定義姿態轉序為2-1-2，對應的歐拉角為θ,φ,φ。星體相對于J2000慣性坐標系的角速度在星體坐標系b中的投影為ω=[ωx,ωy,ωz]，可建立[θ,φ,φ,ωx,ωy,ωz]六變量的姿態運動常微分方程組。

姿態運動方程描述星體相對于交點軌道系的運動規律。歐拉角表示的坐標轉換矩陣為[6]：

(1)

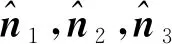
將式(1)代入并整理得：

(2)

其中，上標bx、by、bz表示角速度投影到星體坐標系中各軸分量。

2.2 姿態動力學方程及重力梯度表達式

投影到任意坐標系l的姿態動力學方程[6]：

(3)

式中：I為星體轉動慣量；ω為星體角速度；M為外力矩，本文即為重力梯度力矩；下標bi表示星體相對于慣性坐標系，li表示任意坐標系l相對于慣性系i；上標l表示投影到坐標系l。當投影參考系為星體坐標系b時，式(3)變為：

(4)

(5)

展開可得：

(6)

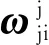
(7)

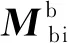
(8)

式(8)中星體轉動慣量I慣量積為0。I與坐標軸的選取密切相關，總可以通過坐標變換將衛星慣量矩陣轉化為慣量積為0的對角矩陣，而且一般的星體坐標系的設置均使得非對角元素慣量積相比對角元素轉動慣量很小。因此，不失一般性，以下僅討論在慣量矩陣為對角矩陣情況下的姿態運動方程。設地心到衛星的矢徑在軌道坐標系和星體坐標系中分別表示為ro和rb，則ro=(0 0 -r)T，rb=R2(φ)R1(φ)R2(θ)R2(u)ro，u為衛星軌道緯度幅角，即從升交點起沿衛星運動方向到衛星轉過的角度。將rb表達式代入(8)式可得：

(9)

3 自旋運動解析解

3.1 解析解的推導

定義萊查坐標系[7-8]為先繞交點軌道系y軸轉動θ，再繞新的x軸轉動φ形成的坐標系，θ為進動角，φ為章動角；星體坐標系b即為萊查坐標系繞自身y軸旋轉一個自旋角φ形成。

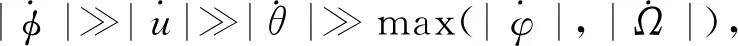
用下標l表示萊查坐標系，式(3)即為投影到萊查坐標系的姿態動力學方程，將式(3)寫為：

(10)

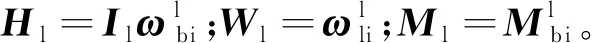
(11)

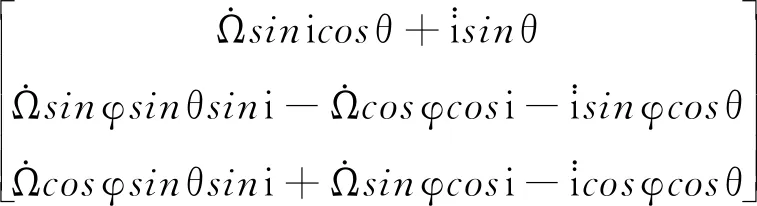
(12)

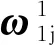
(13)

投影到萊查坐標系的轉動慣量Il=R2·(-φ)IbR2(φ)，由式(11)～(13)可得到H1的分量為：

(14)

(15)

(16)

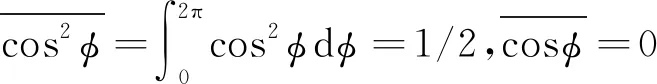
萊查坐標系下的重力梯度力矩Ml為：

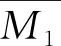
(17)

由式(14)(15)，略去4階以上小量，得到：

(18)

(19)

式(17)～(19)代入式(16)，并略去2階以上小量可得：

俗話說，有好的思路，把它變成現實才是最重要的。“科學發展觀”的基本要求是全面協調可持續，就是要推進各個方面的發展，實現速度、質量、效益統一，而不能顧此失彼。“科學發展觀”的根本方法是統籌兼顧，也就是要統籌解決生產建設中的各種關系和問題。而這一切都離不開高質量、高效能的管理。為此，我們需要時刻保持拼搏進取、勇創一流的精神狀態，始終堅持以追求卓越為目標，持之以恒地抓好“制度建設、管理模式、管理效能”這三個關鍵環節，全面提升管理標準和水平，探索形成高質量、高效能的管理模式，為全面協調可持續發展奠定堅實的管理基礎。

(20)

令：

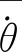
則式(20)中cos2(u+θ)可分解為下式：

cos2(u+θ)=

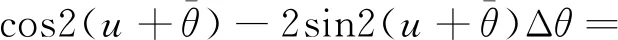
這里略去了小量周期項，代入式(20)，得到進動角、章動角平均值的解析式：

(21)

進動角、章動角的周期項如下：

(22)

進動角和章動角平均變化速率為：

(23)

3.2 自旋運動規律及解析解成立的條件

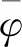
(24)

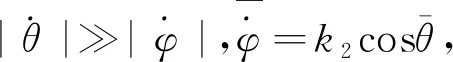
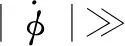
(25)

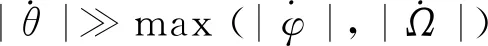
(26)

4 數值仿真分析及對解析解的驗證

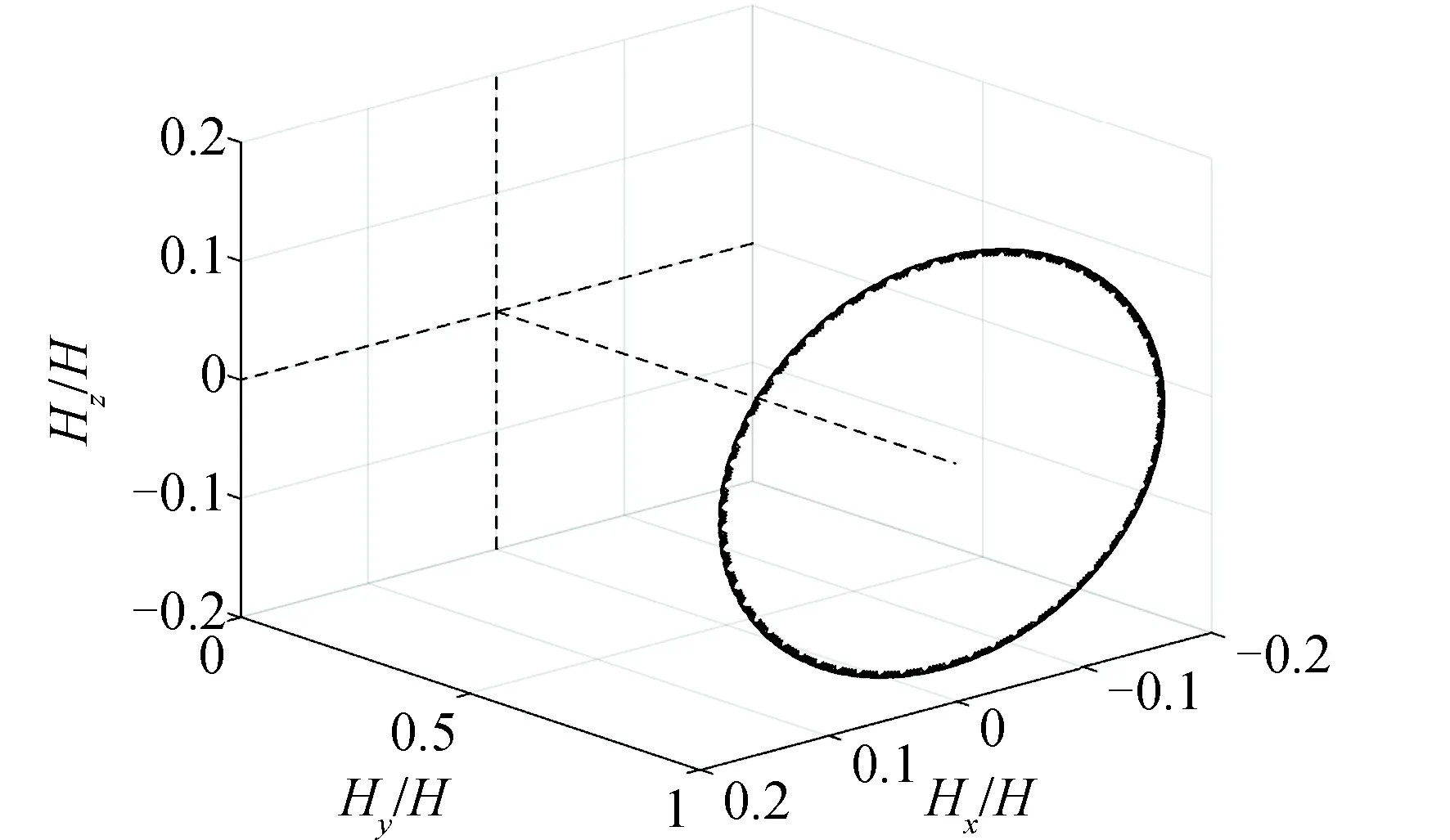
圖1 角動量空間運動Fig.1 Spatial motion of angular momentum

以方程(2)(4)建立常微分方程組，采用數值積分仿真分析。初值設計衛星繞最大主慣量軸自旋，設為衛星本體y軸，初始條件為：

(27)

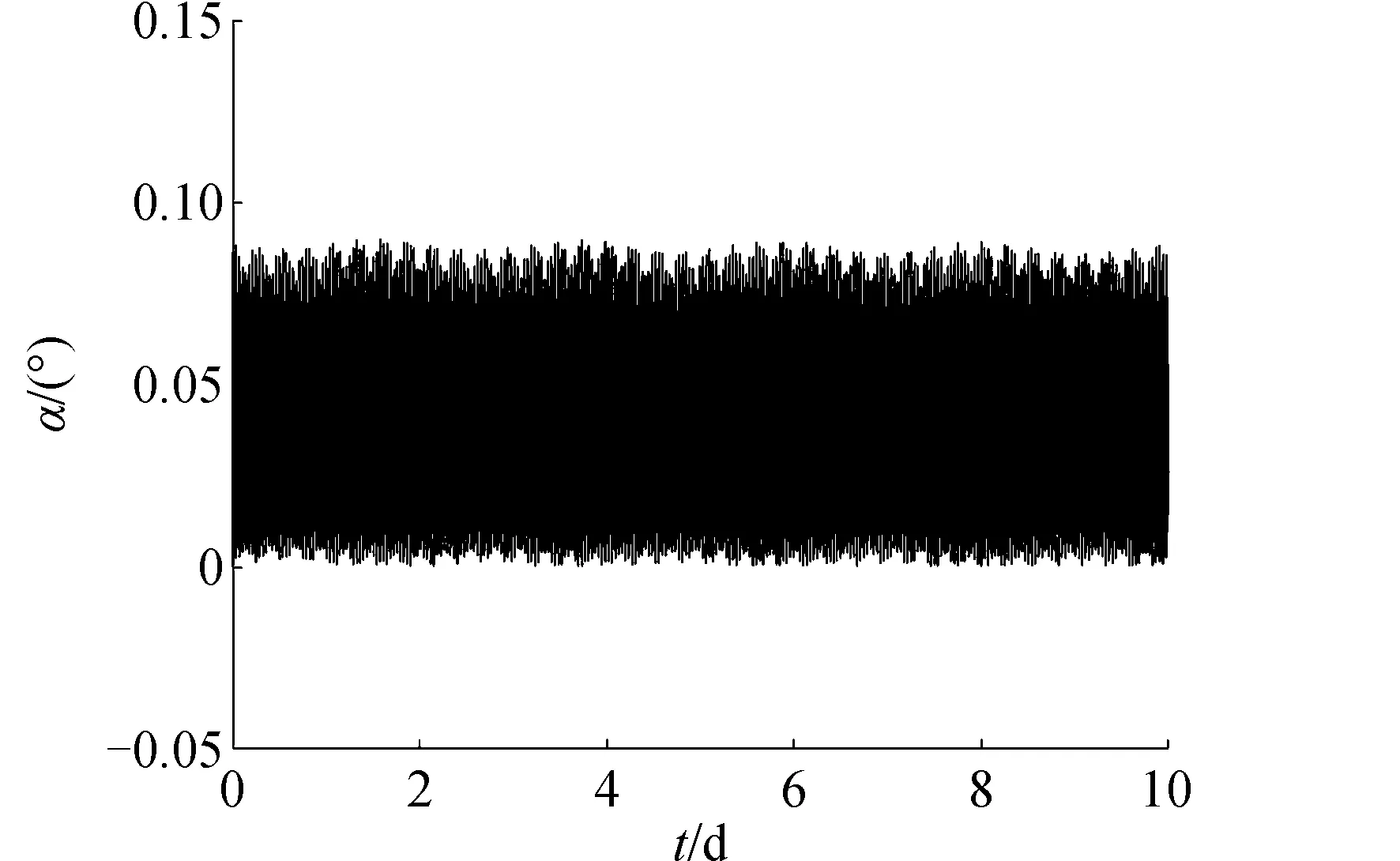
圖2 角動量方向與自旋軸夾角αFig.2 Angle α between angular momentum direction and spin axis

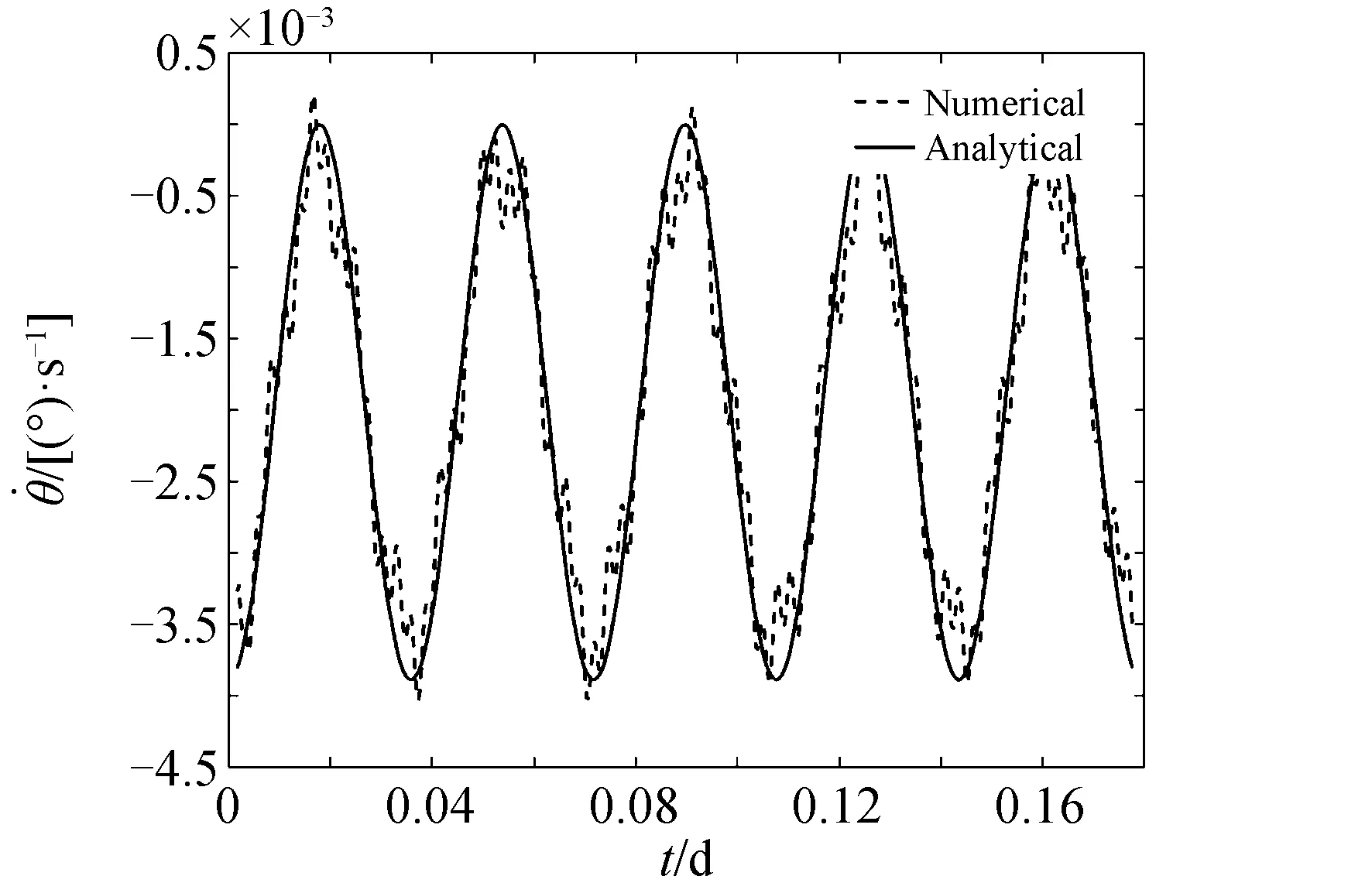
圖3 進動角速度數值解與解析解Fig.3 Numerical and analytical solutions of precession angular velocity

圖3是進動角速率變化曲線，虛線為進動角速率按照自旋角φ求平均的結果，進動角速率仍存在周期運動，周期近似為軌道運動周期的一半，實線為式(23)確定的常量加式(22)確定的周期項，可見數值曲線和解析解曲線符合得很好。圖4和圖5分別是進動角和章動角變化曲線，實線表示解析解，為式(21)確定的平均值加上式(22)確定的周期項，初值取平均值即式(27)中的初值減去式(22)確定的周期項。圖4符號“*”連接的曲線為進動角數值解，與解析曲線符合得很好，進動角近似線性變化；圖5虛線部分為章動角數值解，解析解給出的平均值曲線在數值解包絡中間。章動角在衛星運行10d軌道面進動接近10°后，仍然保持在初值附近小幅波動，說明自旋進動和章動運動跟隨軌道面一起進動，圖1顯示的自旋軸空間運動也說明這一點。由圖3～5可見，解析公式(21)～(23)計算的進動角、章動角及其變化曲率計算結果與數值計算結果非常接近， 這就說明了解析公式的正確性。

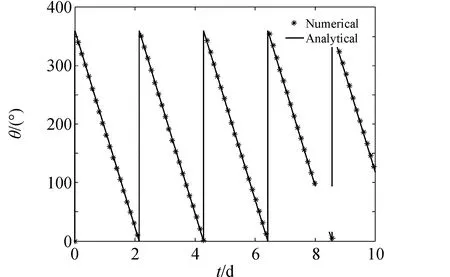
圖4 進動角θ數值解與解析解Fig.4 Numerical and analytical solutions of precession angle θ gradient

圖5 章動角φ數值解與解析解Fig.5 Numerical and analytical solutions of nutation angle

5 結論

本文推導了重力梯度力矩作用下近地衛星自旋運動的解析公式，分析其運動規律為：近地衛星受地球非球形等主要攝動影響，衛星軌道面緩慢進動，當衛星繞最大主慣量軸旋轉且自旋角速度在一定取值范圍時，自旋軸以恒定的平均角速率進動，進動軸接近軌道法線，章動角在小范圍內波動，波動周期與進動周期相同；進動角速率與衛星軌道高度、自旋轉速、三軸轉動慣量及章動角有關；衛星的進動、章動和自旋運動隨著軌道面的進動一起進動。

衛星失控自旋后由于能量耗散作用，最終繞最大主慣量軸自旋，利用解析公式，可以在已知自旋軸進動角速率和自旋轉速情況下(一般星上傳感器容易測得)，計算自旋軸與軌道法線夾角的姿態信息，這就為衛星失控自旋后的姿態確定提供了理論依據。當衛星發生姿態測量元件或者部分姿態控制部件故障后，可以建立適當的衛星自旋姿態，由于自旋軸方向隨軌道面一起進動，且軌道面隨太陽同步進動，因而能夠在衛星姿態測量部件和控制部件關閉的情況下，保證太陽能翼板穩定接收太陽能；同樣的設置可以應用在衛星在軌備份，當設置適當的自旋狀態后，可以關閉一切姿態測量部件和控制部件，衛星仍能保持姿態穩定、能源穩定的測控穩定，實現長壽命在軌保持，需要時可快速激活使用。