深度學習視角下初中數學微專題教學的實踐與反思*
周玉俊 趙 軍
傳統的單元教學,無論是新授課還是復習課,往往局限于某個單元,缺少知識的前后聯系和對教學內容的關聯重組,教師在教學中也往往忽視學生的主動參與和對知識的深度理解。在教學中充分調動學生的主動性,激發其學習興趣,培養良好的思維習慣和思維品質,需要教師更新教學理念,創新教學方法,重視學材重組和教學形式的變化。
近年來,筆者對“微專題”教學進行了一些嘗試和探索,發現它是一種有效的學材重構方式和教學組織形式,可以激發學生學習的內在動力、提高學習效率,幫助學生加深對知識的理解,提升思維能力,培育核心素養。本文擬結合具體的教學案例,談談對“微專題”內涵價值的理解以及對教學實踐的一些思考。
一、對“微專題”內涵的理解
受書面形式的制約,教材的編寫往往具有一定局限性,教材固定的、規范化的形式限制了學科知識中隱含的豐富的思維過程的表達。“微專題”的開發和實施正是為了克服教材的這一局限性,力圖通過學材重構和深度教學,實現從教材“冰冷的說理”到教學“火熱的思考”的轉化與融合。
微專題本質上是一種以學習“四基”、發展“四能”、提升學科素養為指向的學材重構方式,和集靈活性、創新性于一體的教學組織形式。微專題通常是在教授新課或單元復習過程中,圍繞一個或幾個緊密相關的知識或思想方法,形成一個專題研究。微專題也可以理解為針對某個特定目標,結合具體學情設計的、能夠在短時間內解決的“問題集”,這些問題集以知識和題型為載體,注重知識的前后聯系和方法之間的本質關聯,注重思想方法的引領和解題經驗的積累,往往具有因“微”而專、因“微”而深、見微知著的特點。
二、“微專題”的教學價值
微專題教學以“立德樹人”為核心價值,以知識深度加工、思維深度發展、意義深度建構為價值追求,以理解、應用、綜合、評價、創造等高階認知活動為主要學習形式,追求深度教學和深度學習。微專題的教學價值主要表現在以下三個方面。
1.有利于激發學生的學習動力,促進積極的情感體驗。
相對于日常的新授課和復習課,微專題教學基于具體學情,立足學生學習的“最近發展區”,設計方法和教學形式靈活多樣。知識的關聯、教法的選用既重視學生的學科知識基礎,更關注學生生命成長,重視學法指導,充分激發學生學習的內驅力,為深度學習創造和諧樂學的良好氛圍。
2.有利于提高學生的學習效率,發展“四基”、培養“四能”。
微專題通常以課本上的典型例題、習題為載體,以“一題一課”“一圖一課”“一法一課”等形式展開教學,注重關聯前后的數學知識和解題方法,力求將零散的知識技能、數學思想和活動經驗串聯成線,使學生能夠舉一反三、觸類旁通。微專題教學以“問題鏈”為主要教學形式,注重培養學生發現問題、提出問題、分析問題和解決問題的能力,最大程度提高學生的學習效率,減輕學習負擔。
3.有利于促進學生的深度學習,提升學科核心素養。
微專題的實施以認知心理學原理、主體教育論、建構主義理論為指導,立足學生的認知基礎,著力解決學生學習中的重點和難點問題,教學實施采用“題組+變式”的方式,促進學生主動學習、深度學習,注重培養學生的學習力和思維力,發展學生的創新意識和探究能力,提升學科核心素養。
三、“微專題”教學案例:《“圓”來如此》
1.追根溯源,“一中同長”。
引例:蘇科版九年級數學上冊第38頁,圓的集合定義。
師:如圖1,通過操作、觀察可以發現,圓是由怎樣的點形成的集合?
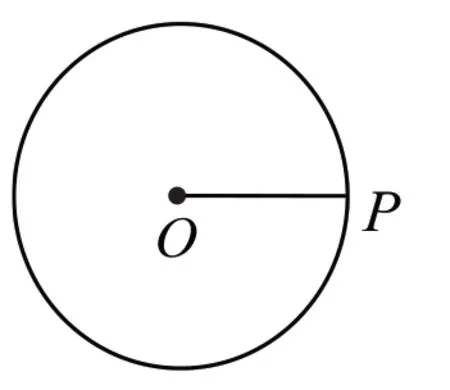
(圖1)
生:圓是到定點(圓心O)的距離等于定長(半徑OP)的點的集合。
【教學意圖】通過復習圓的集合定義,引導學生體會“一中同長”的含義,為后續解題過程中添加輔助圓解決問題打下理論基礎。
2.變換載體,靈活運用。
探究1:“圓”來如此求角度
問 題1:如 圖2,四 邊 形ABCD中,BC=DC=AC,∠ACB=68°,∠ADB=______。
師:由條件BC=DC=AC可得哪幾點共圓?
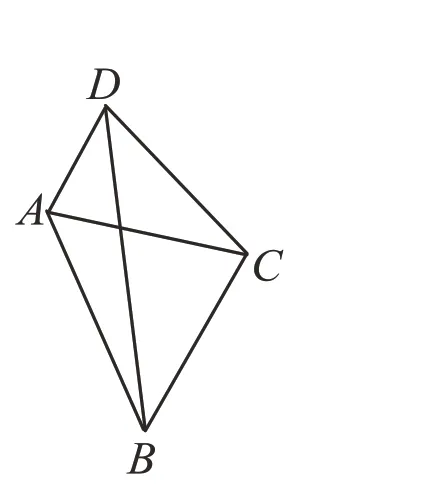
(圖2)
生:BC=DC=AC可以理解為B、D、A三個點到點C的距離相等,如圖3,以點C為圓心、BC長為半徑畫圓,則點B、D、A都在這個圓上。
師:此時如何求∠ADB的度數?
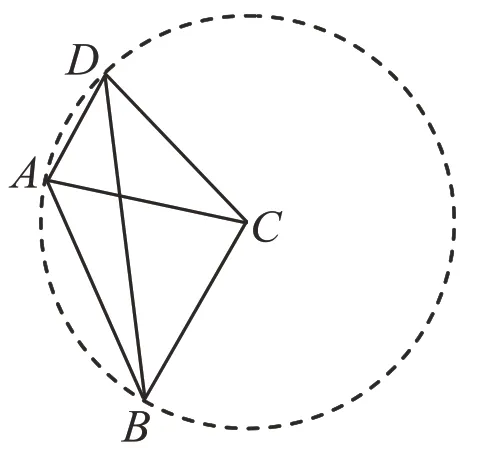
(圖3)
生:此時∠ADB與∠ACB的關系實質上就是弧AB所對的圓周角與圓心角之間的關系,由此可以求出∠ADB的度數。
【教學意圖】由引例中圓的“一中同長”特點,讓隱形的圓顯現,使學生經歷“從無圓到有圓”的思考過程,體會找到圖形中隱藏的圓之后解題的方便與快捷。
探究2:“圓”來如此求最值
問題2:如圖4,H是正方形ABCD內的一點,且AH⊥BH,連接DH,若正方形的邊長為2,則線段DH長度的最小值是______。
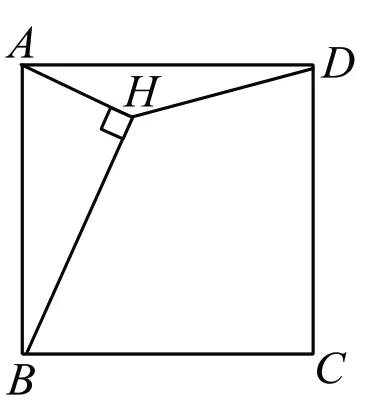
(圖4)
師:由點H是動點,且AH⊥BH,你能想到什么?
生:點H到AB中點的距離保持不變,始終等于斜邊AB的一半。
師:結合圓的集合定義,點H在什么圖形上運動?
生:點H在正方形內部,且在以AB為直徑的半圓上運動。
師(追問):如何求DH的最小值?
-生:如圖5,可以看為⊙O外一點D到圓上的最短距離。
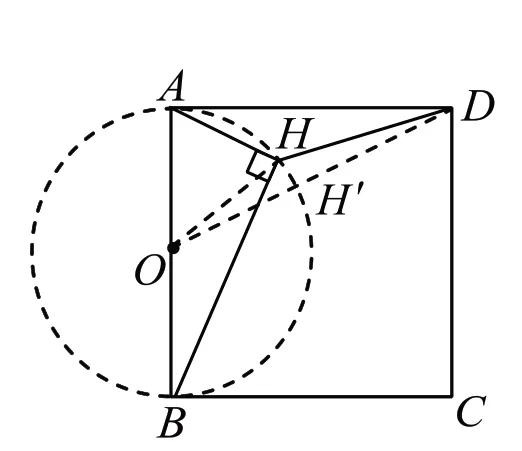
(圖5)
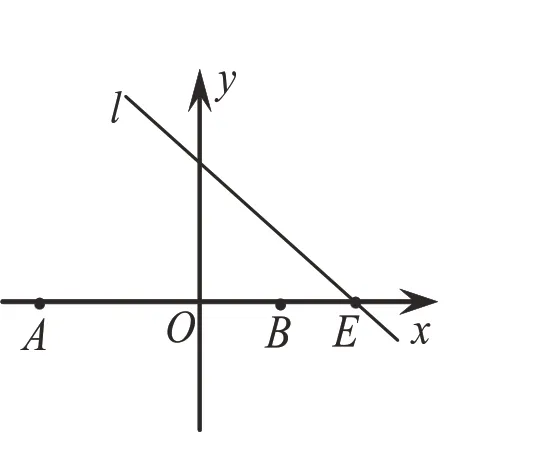
(圖6)
【教學意圖】引導學生審題,明確點H到AB中點的距離保持不變,從而聯想到點H的運動軌跡是一段圓弧,將問題轉化為“圓外一點到圓上點的最小距離”,達到“化動為靜、建構模型”的目的。
探究3:“圓”來如此求表達式
問題3:如圖6,在平面直角坐標系中,點A(-4,0),點B(2,0)。若直線l過點E(4,0),M為直線l上的動點,當△ABM是以點M為直角頂點的直角三角形時,求直線l的表達式。
師:如何確定點M的位置?
生:如圖7,根據圓的集合定義,以AB為直徑作⊙C,點M一定在這個圓上。
生(補充):因為M為直線l上的動點,所以當直線l與⊙C相切時,切點即為點M。
師(追問):這樣的點有幾個?如何求此時直線l的解析式?
生:兩個,問題的關鍵是求D點坐標,可借助△CEM≌△DEO,求得OD=MC=3。
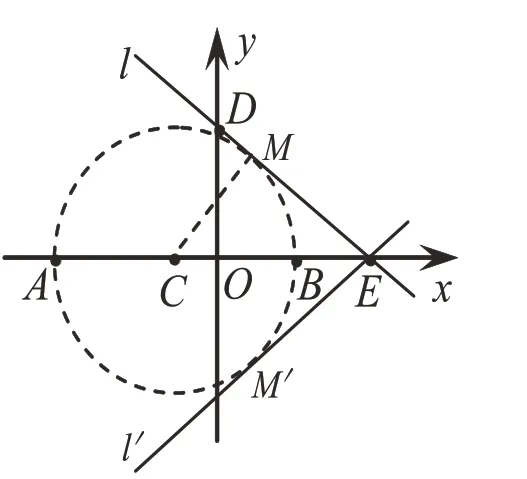
(圖7)
【教學意圖】教師在引導學生分析出點M運動的軌跡后,將隱性的圓顯性化,再利用圓的性質確定直線l的位置,彰顯“‘圓’來如此”的魅力。
3.歸納小結,“圓”來如此。
師:回顧本節課所解決的問題,我們會發現始終有一個“隱形的圓”貫穿“題”中,歸納一下,什么情況下我們可以通過構造圓來解決問題?
生:在“有幾條線段共端點且等長”或者“直角頂點在運動”的情況下可以通過構造圓來解決問題。
【教學意圖】通過歸納小結,讓學生重新審視“添圓法”的巧妙之處,加深對構造輔助圓的條件的理解,完善方法體系,構建“多題一法”,實現因“微”而專、見微知著的目的。
四、教學思考
微專題應當基于教情、立足學情,根據具體的教學內容靈活設計并實施。在教學過程中要突出以生為本,因情施教、按需施教,例題應根據學情選用。以此類推,微專題教學應遵循“從實踐中來,到實踐中去”的指導思想,堅持“開發—實踐—修正—再實踐—再修正”的實施路徑,增強教學的有效性和針對性。
1.堅持以生為本,突出主體性。
主體性是微專題設計和實施的首要原則。微專題的設計要面向全體學生,從具體學情出發,把握好低起點、快反饋、多層次、富挑戰、重實效的要求,體現基礎性、層次性和綜合性的特點。上述課例中對“添圓法”的教學設計就體現了這樣的特點:首先,《“圓”來如此》這個標題足夠吸引學生,蘊含著“添加了圓之后不過如此”,有化難為易之意;其次,對題目的安排由易到難、由淺入深,問題設置富有啟發性。所以,微專題教學必須始終堅持以學定教、因材施教、學為中心、以教促學。
2.堅持因需而教,注重靈活性。
靈活性是微專題設計和實施的一個重要特征。微專題的設計方式靈活多樣,可以是對某個知識板塊的專題復習,也可以是對某些數學模型的變式探究,還可以是對某種數學方法(如旋轉法、分析法等)進行指導的專題,抑或是某種“數學思想”(如化歸、分類等)體悟的專題等,設計內容和上課形式不拘一格、靈活機動,教學實施注重相機而教、靈動生成。上述課屬于“多題一法”,結合學情,我們還可以從“一題多法”、逆向編題等方面展開微專題的開發與實踐。
3.堅持實踐創新,體現適切性。
適切性是微專題設計和實施的質量保證。微專題教學的目的在于以教學設計為載體,幫助學生發展思維、提升素養,實現高效、高質、深度的學習。微專題教學的有效性要通過教學實踐加以檢驗,注重校正優化以及再實施再優化的過程。上述課例在實際教學時一定要根據學情對題目進行增減,以讓學生“跳一跳夠得著”為標準,一切從實際出發,不能一味貪多求深。
在微專題教學的實施過程中,每一個專題都要盡量做到“小開口,大方法”。在選題上力求以小見大、微中見法,將某一方法、思想、技巧、模型深入剖析、歸納提煉,形成一系列互相獨立而又相互關聯的微專題案例。在具體的實施過程中,需要著眼于學生的思維發展、能力提升和數學素養的形成,將微專題的開發、實踐與深度教學、深度學習相結合,與學生創新精神和實踐能力的培養相結合,有效地提升學生的綜合素質。

