考慮電池損耗的電動冷藏車路徑及充電策略

王嘉月，史 立

上海海事大學 物流科學與工程研究院，上海201306

電動汽車具有“零廢氣排放”的優點，得到世界各國政府對新能源汽車開發的推崇[1]。隨著我國國民收入提高，冷鏈物流擁有很大發展空間，將電動冷藏車用于生鮮產品配送已成為物流發展趨勢。

電動冷藏車受到電池容量的限制，需在送貨途中前往充電站進行充電。現階段充電技術尚未成熟，嚴重影響電動冷藏車的續航里程，進而影響運營成本。如何科學有效地規劃配送路徑，減少充電次數、降低電池損耗成為冷鏈物流發展的研究熱點。胡紀玲[2]建立了包括固定成本、行駛成本、制冷成本、時間窗成本和貨損成本在內的電動冷藏車路徑規劃模型，并通過改進粒子群算法進行了求解。馮杰等[3]將充電成本加入傳統VRP模型目標函數中，建立有軟時間窗約束的生鮮產品純電動冷藏車路徑規劃模型，采用蟻群算法測試算例證明模型的實用性。

目前研究電動冷藏車VRP問題的文獻較少，可從普通電動汽車路徑問題以及傳統冷藏車配送路徑問題的文獻中尋找研究的方法。Lin等[4]提出了考慮車輛負載對電池消耗影響的EVRP模型，以最小的行駛時間成本、最小的能源成本和最優的電動汽車調度策略為目標，并通過Austin TX案例分析說明車輛負載對路徑策略的影響。Schneider等[5]提出了帶有時間窗和充電站的電動汽車路徑問題（EVRPTW），同時考慮了車輛的有限運載能力以及客戶時間窗約束，并設計了一種混合啟發式算法，將變鄰域搜索算法與禁忌搜索啟發式算法相結合，對模型進行了有效的求解。楊珺等[6]結合電動汽車換電站選址以及配送路徑問題建立了整數規劃模型，并設計了一種禁忌搜索-改進C-W節約的兩階段啟發式算法對模型進行求解。馮鵬翔[7]在考慮裝載容量等因素基礎上整體規劃了電動汽車的選址和路徑，以減少建設配送系統的總成本。郭放等[8]將充電時間和電池損耗成本納入目標函數并使用多階段啟發式算法進行求解，結果證明了在配送距離不變或略有增加的情況下，考慮充電時間與深度放電成本的模型可較大幅度減少充電時間與電池損耗成本，降低企業運營成本。Miroslaw等[9]在保證生鮮產品質量以及滿足客戶的送貨服務時間窗要求的基礎上，將冷藏車車廂溫度控制作為約束條件建立成本最小化的車輛路徑模型。Osvald等[10]將運輸過程新鮮蔬菜的易腐性作為構建模型的關鍵因子，采用基于禁忌搜索算法的啟發式算法對帶有時間窗約束的數學模型進行了求解，并利用改進的Solomon問題驗證了算法的性能。

綜合來看，電動車路徑優化問題研究大多集中于路線長度的最短化，很少將充電對電池造成的損耗納入運營成本考慮范圍。文章建立的電動冷藏車路徑優化模型與現有研究主要區別在于將電池損耗成本加入電動冷藏車的路徑優化目標函數中，通過分析不同充電上限情況的各項成本，得到電動冷藏車的最佳充電策略。

1 電動冷藏車配送路徑優化模型

電動冷藏車路徑優化模型以運輸成本、制冷成本、貨損成本、懲罰成本、充電時間成本、電池損耗成本構成的總成本最小為目標函數。

1.1 模型假設

（1）配送中心配送單一產品，有k輛相同的電動冷藏車，最大載重量和電池容量均已知；

（2）客戶需求都會被滿足且只能由一輛車服務；

（3）冷藏車從配送中心出發，最終回到配送中心；

（4）每個客戶有時間窗約束，未在規定時間內送達會產生相應的懲罰費用；

（5）配送中心對客戶的需求、位置以及充電站位置已知，車輛從某一點出發，其下一客戶位置已確定，不會改變；

（6）車廂外環境溫度變化只對冷凍設備消耗造成影響，運輸過程中冷藏車廂內溫度恒定，貨物腐壞只與運輸時間有關；

（7）車輛從配送中心出發時為滿電狀態，電量不足可進入充電站直接充電；

（8）不考慮交通擁堵情況，配送時間段道路通暢。

1.2 參數符號

（1）模型集合。

O：配送中心集合，用{}o表示單一配送中心；

L：表示客戶點的集合；

E：充電站集合；

V：所有頂點的集合，V=O?L?E；

D：表示路段的集合；

K：配送車輛集合，配送車輛用k表示，k∈K。

（2）模型涉及的其他相關參數，如表1所示。

表1 參數說明Table 1 Parameter specification

1.3 數學模型

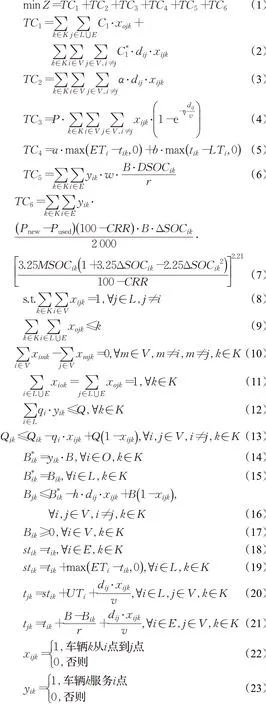
其中公式（1）為目標函數，表示電動冷藏車配送總成本最小；式（2）～（7）分別表示運輸成本、制冷成本、貨損成本、懲罰成本、充電時間成本、電池損耗成本，式（7）根據文獻[11]電池容量衰退成本模型構建，以此估計電池損耗成本；式（8）～（21）為約束條件：式（8）表示每個客戶只能被一輛訪問；公式（9）為車輛約束，提供服務的電動冷藏車數量不得超過配送中心車輛總數；式（10）表示每個節點到達的車輛數和離開該節點的車輛數一致；公式（11）表示配送冷藏車只能從配送中心出發一次且最后回到配送中心；公式（12）表示裝載量不能超過車輛的最大載重量；公式（13）表示裝載量與客戶需求量之間的關系，冷藏車從客戶點j離開時的載重量等于車輛離開i點時的剩余載重量減去客戶j的需求量；式（14）表明電動冷藏車從配送中心出發時電量為充滿狀態；公式（15）表示冷藏車在客戶點服務期間不消耗電量；式（16）表示車輛行駛里程與耗電量之間的關系；式（17）確保電動冷藏車有足夠的電量訪問每個節點；式（18）表示電動冷藏車進入充電站可以直接充電，無需排隊等待；式（19）表示如果車輛提前到達客戶點，則需要等待至客戶要求的開始服務的時間；式（20）表示冷藏車到達下一客戶點j的時間為上一客戶點i開始工作的時間、客戶點i的卸貨時間以及車輛從客戶點i到客戶點j的行駛時間三者的總和；式（21）表示如果車輛進入充電站充電，則冷藏車到達下一客戶點j的時間等于車輛到達充電站的時間加上車輛充滿電的時間以及車輛從充電站到客戶點j的行駛時間；公式（22）和（23）為0-1決策變量。

2 粒子群算法設計

2.1 算法原理

粒子群算法的基本原理是粒子通過種群中個體之間的信息共享和協作在解空間搜索最優解。陳自郁[12]認為粒子群算法的基礎是粒子間的信息共享，有效利用信息是信息共享機制的核心問題。文章結合閆雪麗等[13]提出的隨機歷史全局最優與局部最優相結合的粒子群算法（RCHGLBPSO）對模型進行求解，通過增加一種粒子共享信息的類型來擴大搜索的區域，防止算法早熟收斂。粒子i隨機選取互不相同的m（固定的）個粒子作為鄰域子群，通過比較子群中的粒子的適應度值，找到鄰域的全局最優位置并將其應用到位置更新公式中。假設在D維搜索空間中，有n個粒子組成的種群，其中第i個粒子在D維空間位置為Xi=(xi1,xi2,…,xiD)，表示問題的一個潛在解；第i個粒子的飛行速度為Vi=(vi1,vi2,…,viD)，第i個粒子的個體極值為Pi=(pi1,pi2,…,piD)，種群的群體極值為Pg=粒子速度和位置更新公式如下：

其中，t為迭代次數；w為慣性權重；c1和c2是非負常數，稱為學習因子；r1和r2是分布于[0,1]區間的隨機數；Pl=(pl1,pl2,…,plD)表示算法運行到第t次找到第l個粒子的鄰域最優位置賦予歷史全局和鄰域全局信息不同的權重。

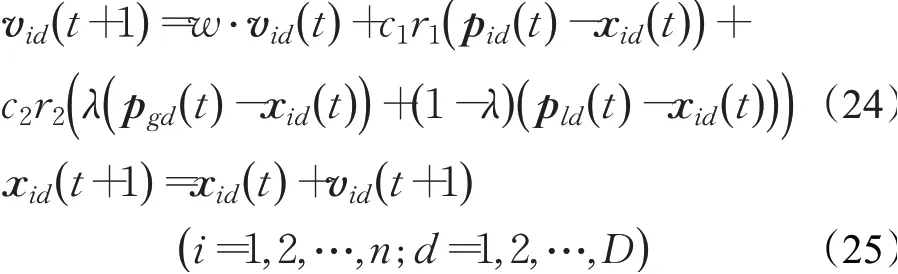
2.2 算法編碼

采用文獻[14]編碼思想，模型中有n個客戶點，為滿足每個客戶由且僅由一輛冷藏車完成服務的約束，將空間向量分成兩個n維向量，分別用Xv和Xp表示。粒子群算法主要用于解決連續性優化問題，而VRP屬于離散組合問題，在求解VRP問題時，要對相關數據進行處理。在每一次粒子位置和速度更新中，需要進行整數化處理。Xv取()1,k之間的隨機數，并向上取整表示客戶服務的冷藏車編號；Xp取()1,n之間的隨機數，將其按從小到大排序即可表示客戶點在各自配送路徑上的服務次序。

2.3 算法步驟

改進粒子群算法步驟如下，流程如圖1所示：

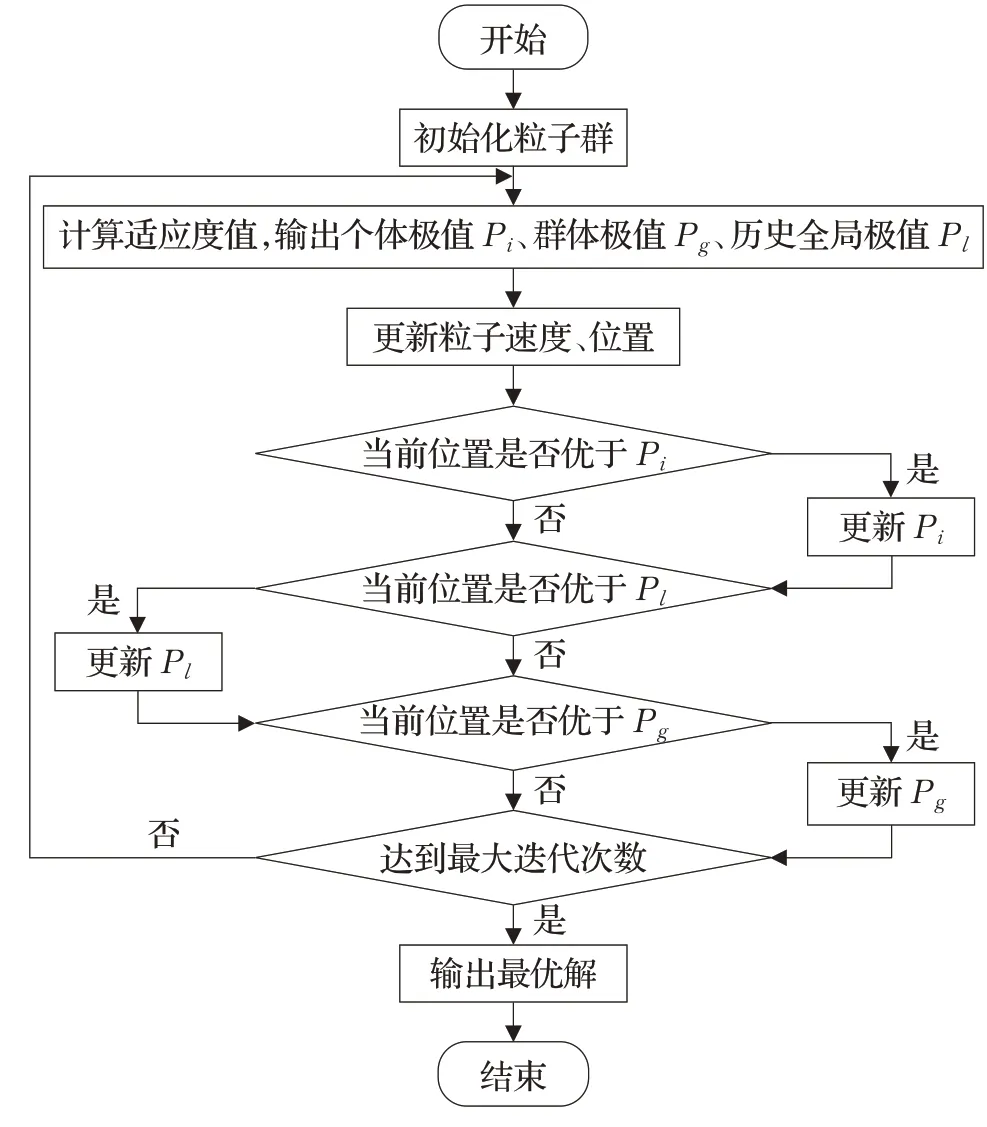
圖1 算法實現流程Fig.1 Algorithm implementation process

（1）設置種群規模、最大迭代次數、鄰居個數等參數，鄰居個數為種群規模的30%，初始化種群，初始化粒子位置、速度。

（2）將模型中的目標函數作為適應度函數，計算粒子的適應度值，尋找個體極值、全局極值、鄰域全局極值，并比較三者的大小。

（3）按公式（24）和（25）對粒子速度和位置更新。

（4）重新計算更新后的粒子的適應度值，據此找尋個體極值、全局極值、鄰域全局極值，同時與上一代粒子極值進行比較，判斷是否進行粒子位置的更新，并記錄全局最優。

（5）判斷算法是否達到最大迭代次數，若達到，算法終止并輸出最優解；否則轉步驟（2）繼續迭代。

3 案例分析

3.1 算法性能分析

利用Rastrgrin函數、Griewankan函數驗證改進粒子群算法的有效性，對改進前后算法均仿真15次。圖2、圖3Rastrgrin函數結果發現標準粒子群算法找到局部最優值，而改進后算法均收斂到函數的最優值且在100代時趨于穩定。圖4、圖5Griewankan函數結果可發現標準粒子群算法易于收斂到局部最優值，而改進后算法均收斂到函數最優值，具有很好的收斂性。綜上改進后的粒子群算法具有很好的收斂性，能快速找到全局最優解。

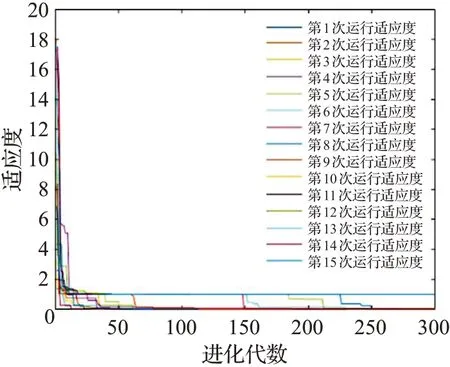
圖2 Rastrgrin函數標準PSO進化過程Fig.2 Particle swarm evolution of Rastrgrin function

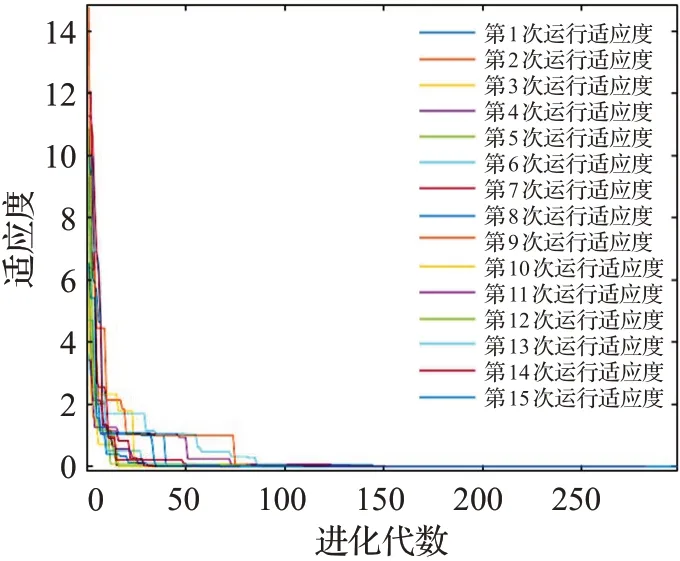
圖3 Rastrgrin函數改進粒子群算法進化過程Fig.3 Improved PSO evolution of Rastrgrin function

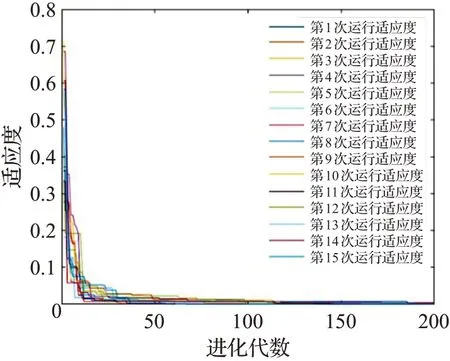
圖4 Griewankan函數標準算法進化過程Fig.4 Particle swarm evolution of Griewankan function

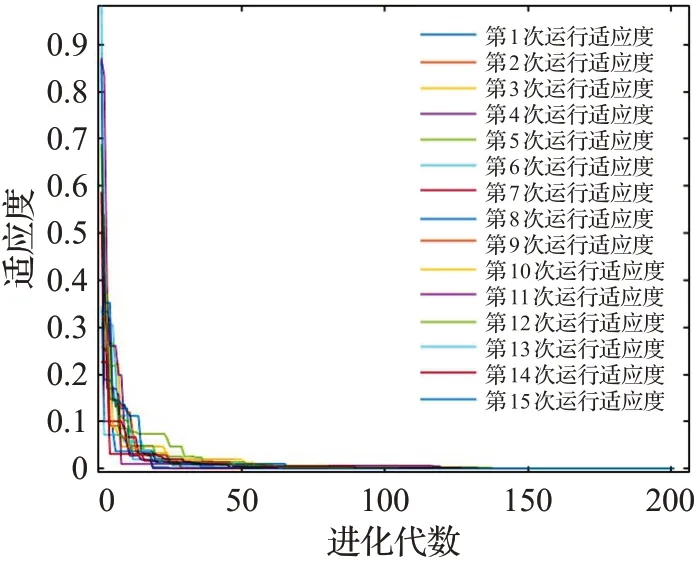
圖5 Griewankan函數改進粒子群算法進化過程Fig.5 Improved PSO evolution of Griewankan function

3.2 案例描述

假設配送中心有電動冷藏車3輛進行單一生鮮產品的配送，每輛冷藏車售價為150 000元，車輛電池的價格Pnew為50 000元，電池額定容量B為80 kWh，最大載重量Q=1.5 t,速度v=60 km/h,耗電系數h=0.6 kWh/km,固定運輸成本C1=100元,單位距離行駛成本C*1=1元/km。冷藏車廂恒溫為-5℃，根據文獻[15]貨損率η設為0.14，產品單價P=100元/t，單位時間充電成本e=1元，單位距離制冷耗電成本α=0.02元/km。在計算退役電池價值Pused時，年折舊率rdep為20%，貼現率rdis為6%，使用年限tuse為8年，Pused為5 579元。電池容量衰減到80%時不能使用，將CRR設為80%。

隨機生成15個客戶點，編號為1～15，隨機產生5個充電站，編號為16～20，配送中心為0，位置為[50，50]，時間窗為[0，15]。各客戶點的位置、貨物需求量、服務時長、服務時間窗信息如表2所示。

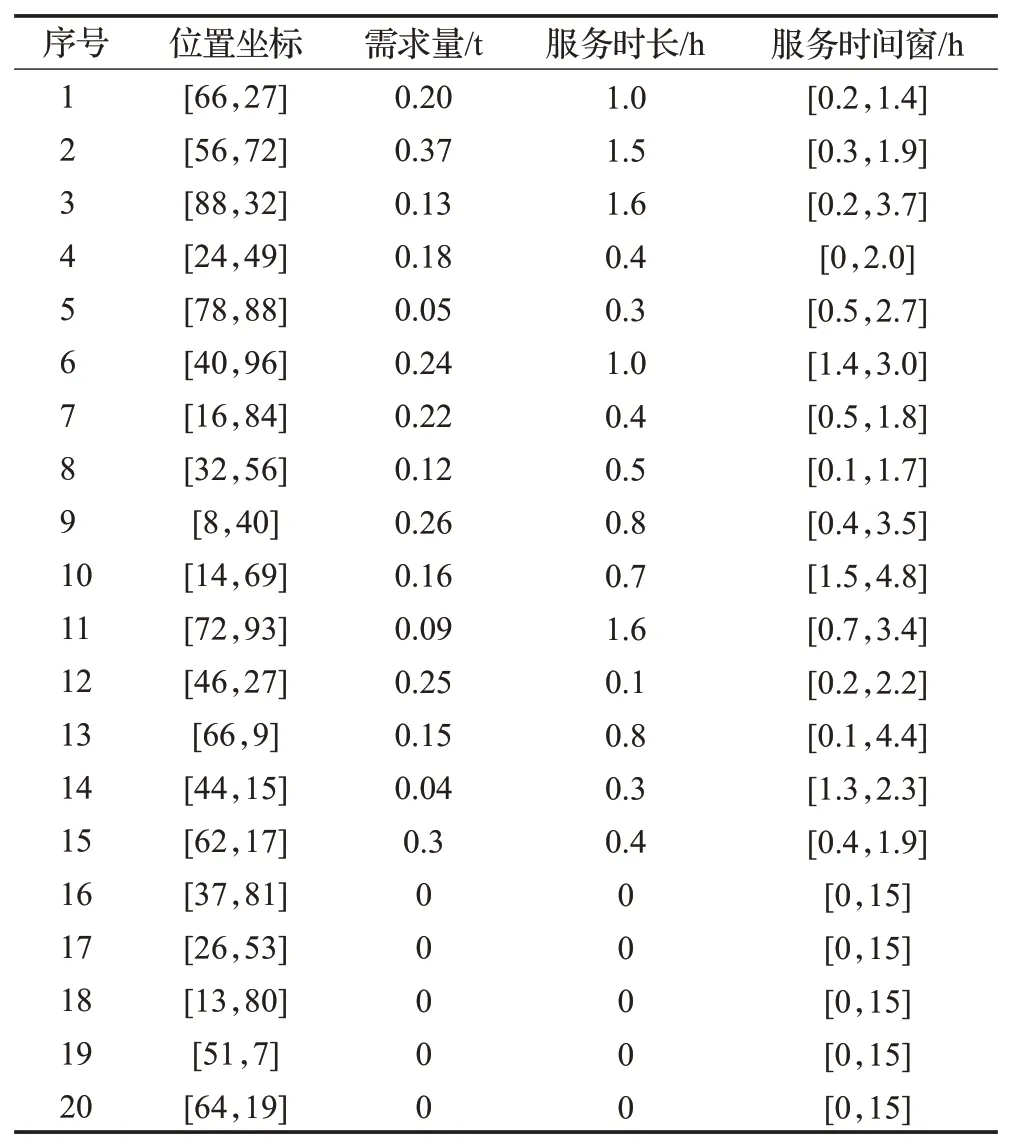
表2 測試數據Table 2 Test data

3.3 優化結果分析

在MATLAB上編寫粒子群算法，設置種群規模為80，最大迭代次數為1 000次，維數為15維，慣性權重w設為0.729 8，學習因子c1=c2=1.496 18。

3.3.1 充電策略影響性分析

將文章提出模型與傳統電動冷藏車VRP模型進行對比分析。將SOC上限設置為100%、90%、80%、70%、60%，考慮到里程焦慮問題，不考慮SOC范圍在10%～50%的情況。SOC上限為100%時（情景一）電池充滿，這與傳統電動冷藏車VRP模型假設一致。通過算法求解得到如表3所示的車輛配送的最優路徑及行駛距離。同時得到了不同SOC上限的各項成本（表4）以及圖6的成本對比。

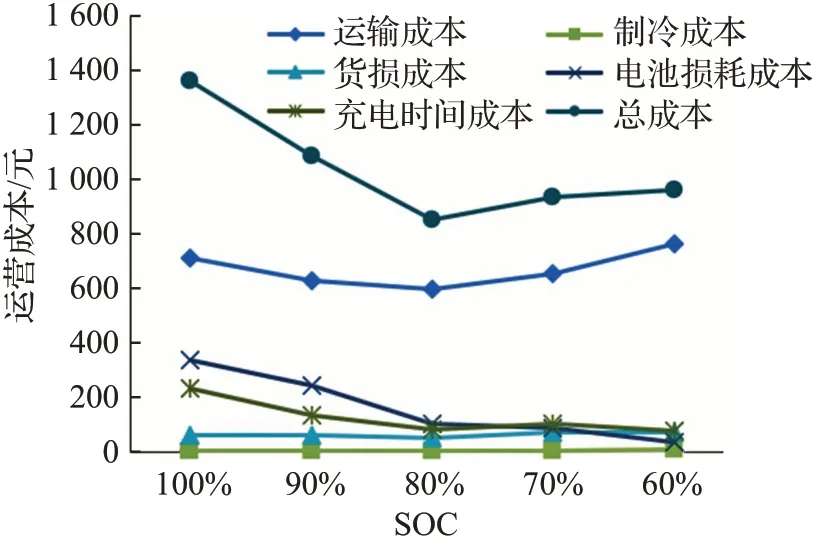
圖6 各項成本對比Fig.6 Cost comparison

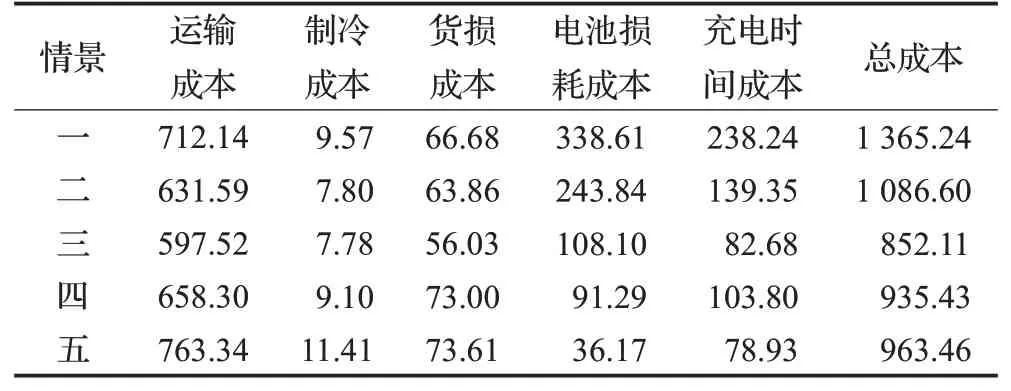
表4 不同SOC上限各項成本Table 4 All costs of different SOC upper limit元

通過表3可知，SOC上限為80%時電動冷藏車以最短的路程完成配送，同時進入充電站充電的次數最少。對比情景一，可發現電量充至80%的路程要比情景一縮短18.63%。

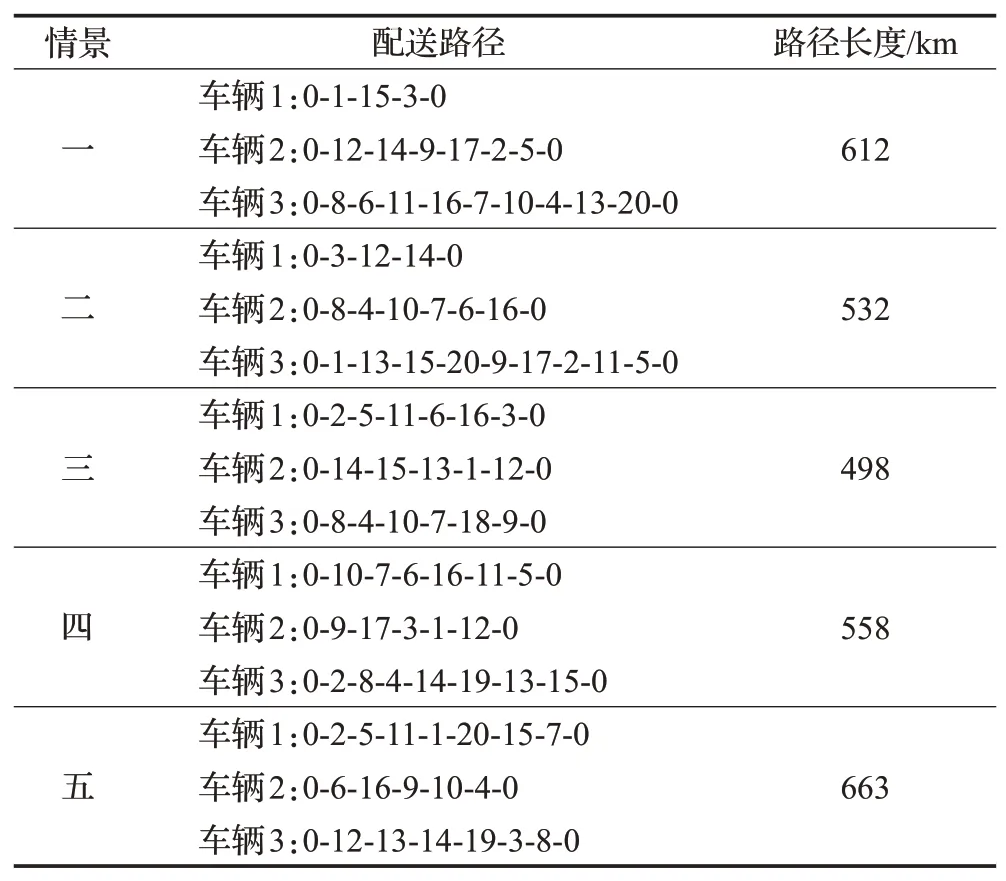
表3 路徑規劃情況Table 3 Path planning situation

由表4可知，情景一總運營成本最高，而情景二至情景五（考慮電池損耗成本）總成本明顯低于情景一，當SOC上限為80%時總運營成本最低。在總成本中，占比較大的有運輸成本、電池損耗成本、充電成本，考慮電池損耗情況可有效影響配送過程的各項成本，對總運營成本、配送路徑等產生作用。

分析圖6可看出：（1）運輸成本方面，情景三的運輸成本為五種情景中最低，對比情景一可發現情景三的運輸成本比傳統模型的節約16.1%；（2）電池損耗成本方面，隨著SOC上限的降低，電池損耗成本呈下降趨勢，充滿電的充電策略對電池損耗最大，而充電至60%對電池損耗最小，電池損耗成本的降幅可達89.32%，即使充電至80%也使電池損耗成本降低68.08%，因此將電池損耗成本納入運營成本計量范圍可有效減小電池損耗；（3）充電時間成本方面，由折線變化看出傳統模型充電時間成本明顯高于本文提出的模型，本文最低的充電時間成本比傳統模型低66.87%，情景三的充電時間成本比傳統模型低約65.3%，考慮電池損耗成本的充電策略在一定程度上節約了充電時間，降低了充電時間成本；（4）從制冷成本和貨損成本變化趨勢可以看出二者一定程度上受車輛行駛距離的影響，因此當SOC設為80%時車輛行駛里程最短，相應的制冷成本和貨損成本要低于傳統模型。綜上所述，電動冷藏車配送時，充電策略可由充滿電轉變為充電至80%，雖然將SOC上限設為80%并不能使電池損耗成本最低，但由于充電策略的改變會大幅度降低電池損耗成本和充電時間成本，有效降低總運營成本。

3.3.2 算法尋優能力對比分析

將充電至80%的充電策略應用于案例中，分別利用標準粒子群算法和本文的改進粒子群算法對案例進行求解，最終得到的優化結果如表5所示。

表5 兩種算法優化結果Table 5 Optimization results of two algorithms

由表5總成本比較分析可知，使用改進粒子群算法求得的解要明顯優于標準粒子群算法的解，通過圖7、圖8的迭代收斂過程可以看出，改進粒子群算法收斂速度更快、收斂性能更好，這表明本文采用的改進粒子群算法在求解電動冷藏車路徑優化問題上的可行性與有效性。

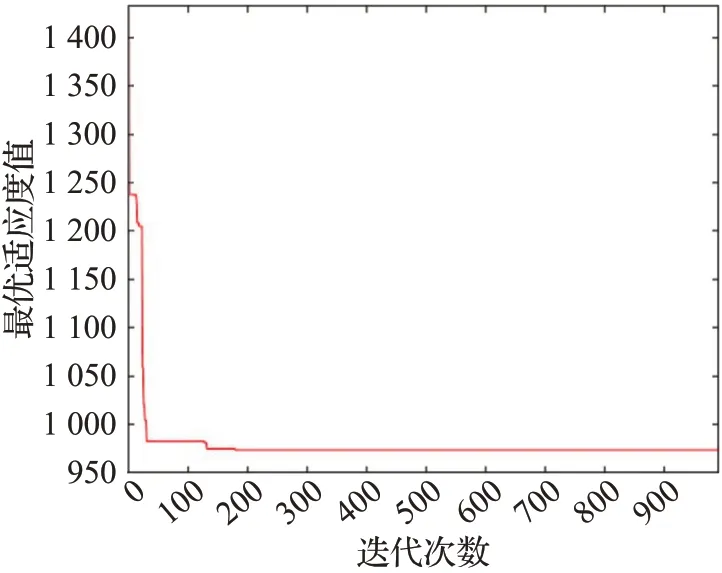
圖7 標準粒子群算法迭代過程Fig.7 Standard PSO iterative process

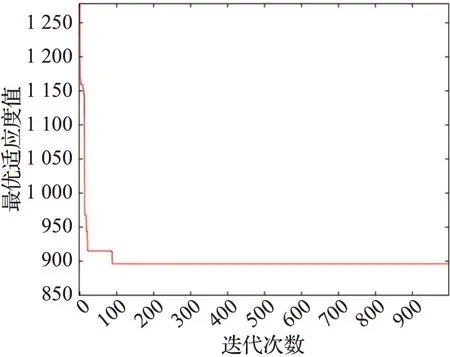
圖8 改進粒子群算法迭代過程Fig.8 Improved PSO iterative process

4 結語

在傳統冷藏車路徑優化問題約束條件基礎上，添加了電動冷藏車的特有條件，同時考慮了生鮮產品的品質動力學模型，構建了包括電池損耗成本在內的電動冷藏車路徑優化問題模型，運用增加粒子間共享信息類型的改進粒子群算法進行求解，為企業提供合理的電動冷藏車充電策略。本模型并未考慮實際充電過程中充電速率變化情況以及回程空載的問題，這也成為后期研究的重要方向。