是“24÷4”,還是“8÷4”
張娜

【摘 要】低年級學生受到年齡特點和學習水平的影響,在解決實際問題時往往隨意、主觀而沒有方法的支撐。教師應注意培養學生良好的解題習慣;采用多元表征等方式幫助學生深入理解題意;輔助學生提煉數量關系,建立方法聯系;經常帶領學生進行回顧和反思,培養檢驗意識。從而把解決問題的過程變成學生提高數學素養的過程。
【關鍵詞】“四清”原則 多元表征 數量關系 判斷檢驗
【問題凝視】
二年級上冊“除法”單元,練習中有這樣一道應用題:
(1)把24本書平均分給3個小組,每個小組分得幾本?
(2)你還能算出每人分得幾本嗎?
第一個問題幾乎沒有人錯,24÷3=8(本),而在解答第二個問題時,學生們的答案五花八門,主要有以下幾種:①24÷4=6(本);②8+4=12(本);③4×2=8(本);④8÷4=2(本)。全班得出8÷4=2(本)的只有少數幾人。通過對比交流,學生們一致否定了第二、第三種方法,而對于第一、第四種方法還是搞不清。很多學生認為第一問的得數是8本,第二問就應該用上第一問的得數來算。那么,到底是“24÷4”還是“8÷4”?
【成因透視】
這是一道圖文結合、連續兩問的應用題。因為第二問中沒有告訴分本子的總數,學生就出現了思維障礙。那么,造成這種現象的原因是什么呢?
(一)學生沒有養成良好的解題習慣
低年級學生在解題時往往急于求成,不讀完題目就開始動筆,或者沒有理解題意就急著解答,不知道怎樣進行有條不紊的思考,這樣就會導致很多不必要的錯誤發生。
(二)學生對于題意理解缺乏數量關系支撐
低年級學生抽象思維能力不夠,不能靈活把握應用題的結構,不善于提煉數量關系。其實,這道題目除了可以根據“一共的本數÷分的人數=每人分得的本數”,還可以根據“每組本數÷每組人數=每人分得的本數”進行解答,而學生缺乏這方面的認知儲備,也就無法與除法建立聯系。
(三)學生對于計算方法缺乏理性思考
低年級的學生年齡小,不夠理性,經常憑自己的感覺想加就加、想減就減,加法不對就用減法,減法不對就用加法。到二年級,學生學了乘法和除法之后,由于四種運算混在一起,學生更加區分不清楚了。如上述第二種答案和第三種答案就是屬于這種情況。寫第一種答案的學生,僅想著用本數去除以人數,卻沒有想清用哪個本數去除以人數才是正確的。
(四)學生對于解題結果缺乏對錯評判
低年級學生思想簡單,對得到的答案不去進行初步的評判。比如由第一問得到“每組8本”,再根據已知信息“每組有4人”,就可以判斷第二問中算出每人6本、12本、8本都不可能,所以第一、二、三種答案都是錯誤的,應該重新選擇正確的方法解答。
【出路審視】
應用題的教學貴在讓學生站在理性的角度充分分析、理解題意,選擇合適的方法,客觀地解決問題。具體可以采取以下幾種策略。
(一)把握“四清”原則,培養解題習慣
好的解題習慣是答對問題的重要保證。在平時的課堂教學中,要培養學生做到“四清”。即“讀清”“想清”“寫清”“查清”。
“讀清”是做題過程中非常重要,而且能反映出學習能力的一個環節。一是“通讀”,將所有的內容一字不漏地讀一遍。二是“重點讀”,就是結合題目圈出關鍵詞和關鍵條件讀。根據低年級學生注意力容易分散這一特點,教師可以要求學生手腦并用,用眼睛看,用手指讀。
“想清”就是動筆前要想清每一句話的意思,特別是對關鍵詞要重點理解。可以想生活中的情況,也可以畫線段圖或簡單實物圖幫助理解,然后確定用什么方法計算。例如:求總數時,把兩部分合起來用加法,求“幾個幾是多少”用乘法;已知總數,求其中一部分用減法,把總數平均分用除法。像這一題求每人分到幾本,就是要把每組分到的本數平均分給4個人,所以應該用除法算。
“寫清”就是在想清的基礎上仔細列式計算,得到答案,要求數字抄對、計算正確。
“查清”包括在每題答完后要從答案的可能性上初步判斷得數對錯,也包括所有練習做完后需要重新讀題理解題意,檢查計算方法和答案的對錯。
這四步的順序不能顛倒。為了讓他們牢牢地記住,養成“讀清”“想清”的習慣,教師還可以用打比方的方法讓他們記住“四清”原則。“讀”“想”“寫”“查”是四兄弟,“讀”是大哥、“想”是二哥、“寫”是三弟、“查”是四弟。他們按序排隊,三弟不能插隊到大哥或二哥的前面。當解答出現錯誤時,教師可以讓學生分析一下自己在哪一步出了問題,是沒“讀清”還是沒“想清”、是沒“寫清”還是沒“查清”。長此以往,學生就能從無意識到有意識,逐步養成良好的解題習慣。
(二)采用多元表征,增強題意理解
應用題的題意有多重表征方式,如利用現實情境中的實物、模型、圖像或圖畫進行的形象表征,利用口語和書寫符號進行的符號表征等,多元表征將幫助學生更好地理解題意。
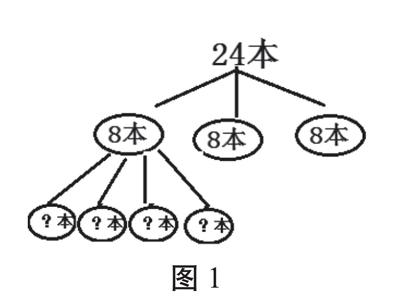
例如,學生對于到底是“24÷4”還是“8÷4”存在疑慮的時候,教師可以創設分本子的情境。先把24本本子平均分成3份,放到每一組,每組幾本?在學生明確做法后,教師追問:“要知道每人分到幾本怎么辦?”學生就會知道只要繼續用每組的8本平均分成4份,得到每人2本。
結合分本子的過程,教師在黑板上逐步畫出圖(圖1)。這時,學生對24本本子兩次平均分的過程就會理解得非常透徹。
所以,在應用題課堂教學中,教師應帶領學生通過多種形式理解題意,通過多元表征,讓學生深深感受到解答應用題的過程中,一切應以題目本身的意思為準,而不能以個人的情感和意志為轉移,逐漸養成良好的數學素養。
(三)提煉數量關系,建立方法聯系
新課標明確指出,要從具體情境中抽象出數量關系,要從實際生活中給學生提供多種形式(如對話、文字、圖表等)的條件和問題,培養學生逐步學會選擇信息、重新組織信息、分析其中數量關系進而解決問題的能力。可見,數量關系的教學在應用題教學中占有重要的地位。
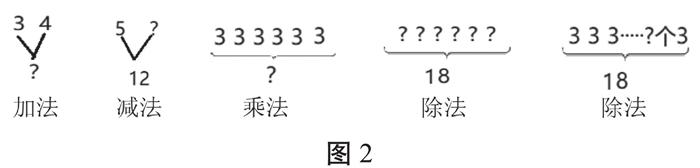
數量關系的提煉能幫助學生進行理性思維的培養,但是低年級學生抽象思維能力弱,數量關系的提煉要在教師的輔助下進行,語言的表達要求不必太高,要適合低年級學生的理解能力和表達方式。除了語言的表達,初學加減乘除應用題時,教師也可以根據題意結合符號的形式進行標注(圖2),目的是使學生理解清楚為什么用加、減、乘或除,使數量關系中的計算方法使用有根據,杜絕方法使用的隨意性,促使學生根據數量間的關系建立理性思考。
(四)適時提醒判斷,強化檢驗意識
在日常教學中,教師要經常帶領學生進行回顧和反思,針對實際情況進行檢驗。要把檢驗作為學生解答問題的必要步驟長期堅持,學生耳濡目染,就會逐步養成自覺檢驗的好習慣,變得更加嚴謹和細致。
例如,本題中出現了四種不同答案:①24÷4=6(本);②8+4=12(本);③4×2=8(本);④8÷4=2(本)。教師就可以先問學生:“這些答案中哪個肯定不對?”判斷排除明顯錯誤的答案,再進一步研究存在疑問的答案,這樣既縮小了研究的范圍,也強化了學生的檢驗意識,培養了學生思維的嚴謹性、批判性和深刻性。
【片段重構】
師:你還能算出每人分得幾本嗎?
生答,師在黑板上寫出所有出現的答案:
①24÷4=6(本);②8+4=12(本);③4×2=8(本);④8÷4=2(本)。
師:這些答案中哪幾個肯定不對?
生1:第2、3種。因為每人分幾本,要把本子平均分,應該用除法計算。
生2:第2、3種。因為每組只有8本,每人的本數肯定不會比8本多,或者一樣多。
師:那“每人分得幾本”到底是“24÷4”還是“8÷4”呢?
師:老師這兒有24本本子,我要把它們平均分給3個小組,誰會幫助老師分一分?
師:每組分到幾本?
生:8本。
師:怎么列式?
生:24÷3=8。
師:為什么用除法算?24表示什么?3呢?8又表示什么?
師:我們用一共的本數÷組數=每組分到的本數。
師:接下來我要知道每人分到幾本怎么辦?
生1:繼續分。
生2:把本子平均分成4份。
師:那么,該用多少本平均分成4份呢?
學生都說8本。
師:8本?為什么不拿24本來分呢?(這是問題的關鍵,得讓學生仔細理解)
生1:24本本子是分給3個組的,不是分給一個組4個人的。
生2:因為24本本子已經平均分給3個組了,每個組分到8本,就要用每組8本平均分成4份。
師:所以,怎么計算每人分到多少本呢?
生:8÷4=2(本)。
師:這里的“8”表示什么?“4”呢?“2”又表示什么?
師:我們用一組的本數÷一組的人數=每人分到的本數。
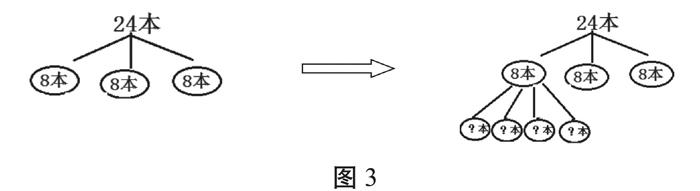
接下來教師讓學生回憶思考過程,并畫圖記錄(圖3)。
通過操作活動和畫圖,學生明確了“一共的本數÷組數=每組分到的本數”“一組的本數÷一組的人數=每人分到的本數”,已知份數要找對應的總數。
美國數學家哈爾莫斯說過,數學家X的一個漏失或一個誤述,正好是數學家Y所需要用以發現真理的東西。學生的一個差錯,可能正好是教師所需要用以幫助學生發現真知的東西。所以,我們對待學生的差錯,不能用“粗心”一詞來打發。教師對于“錯”之所以為“錯”分析得越深,那么學生對于“對”之所以為“對”也就理解得越透。

