多體分離回追現象與方案驗證
李曉軒,楊依峰,張利嵩,秦緒國,戈慶明
(北京航天長征飛行器研究所,北京,100076)
0 引 言
近年來,隨著飛行器任務模式和功能的多樣化,在飛行器方案論證過程中,高速飛行條件下的多體分離問題越來越多。對于多體分離過程,避免分離過程中發生碰撞是需要重點關注的問題[1~4]。本文針對在高超聲速底流區分離時可能遇到的回追碰撞現象進行分析,并通過非定常數值仿真,驗證了一種解決方案的有效性。
1 回追碰撞現象及分離方案
1.1 回追碰撞現象
高超聲速底流區是由膨脹波、回流區、分離激波、尾流激波等流動結構組成的復雜流動區域。馬赫數為15條件下,在飛行器底部,以近似底部直徑為分界面,其內部的流動密度和速度極低,若物體處于該區域內,僅會受到微弱的氣動力作用,如圖1所示。
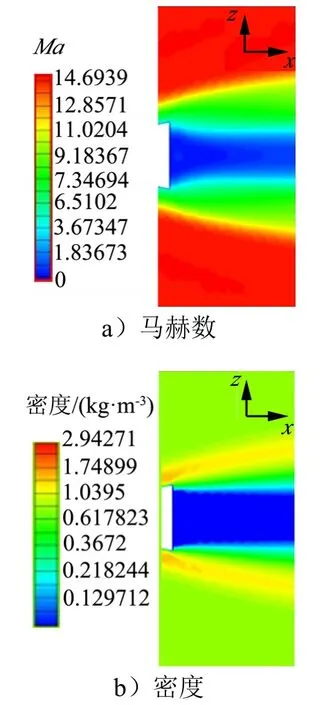
圖1 底流區馬赫數與密度分布Fig.1 Mach Number and Density Distribution in Base Flow Region
回追碰撞過程如圖2所示,當以初始相對速度V0從飛行器底部向后拋出分離體后,分離體將處于動壓極低的底流區區域中,不受明顯的氣動力作用,其相對來流的運動速度近似保持不變。而質量為m的飛行器在氣動阻力Fx作用下,以加速度a=Fx/m做近似勻減速運動,因此飛行器與分離體間的相對速度持續減小,在t=V0/a時減小至Vt=0。之后兩者間的距離將逐漸接近,直至在t=2×V0/a時刻以近似V0的相對速度發生回追碰撞。
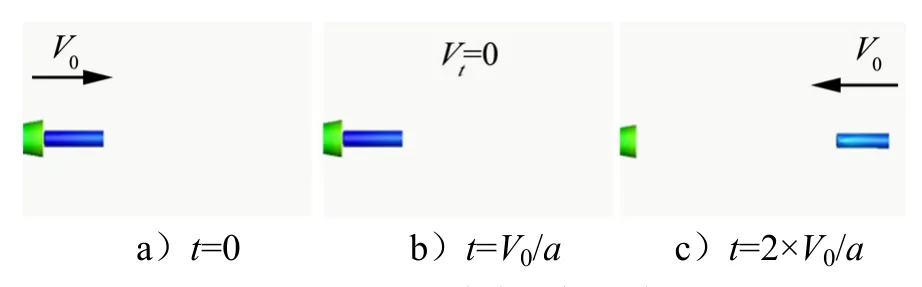
圖2 回追碰撞過程示意Fig.2 Schematic Diagram of Backtracking Collision Process
針對該現象,本文提出后拋+側拋的分離方案,并通過數值仿真對該方案進行了分析。
1.2 分離方案
后拋+側拋方案的大致流程,是將分離體分為左右兩半,首先將其一同向后拋出,在尚未發生回追的時間窗口內,將分離體的左右兩半向兩側進行二次分離,使其飛出低動壓底流區范圍,從而在來流氣動力作用下,向遠離飛行器的方向飛行,避免回追碰撞問題。
2 數值仿真方法
分離過程中飛行器和分離體的位置姿態時刻發生變化,因此根據位置和姿態實時、高效和魯棒的調整網格成為分離過程模擬的關鍵。重疊網格技術中各個獨立網格的拓撲結構不會隨著物體的相對運動而改變,因此基于重疊網格技術的數值模擬方法適于處理剛性物體之間的相對運動。此外還有變形網格技術[5],也適用于多體分離問題的分析。
根據飛行器和分離體的外形特點,采用結構與非結構網格混合的方式,進行了計算網格的劃分。圖3給出了采用重疊網格技術對多體動態問題的仿真流程。
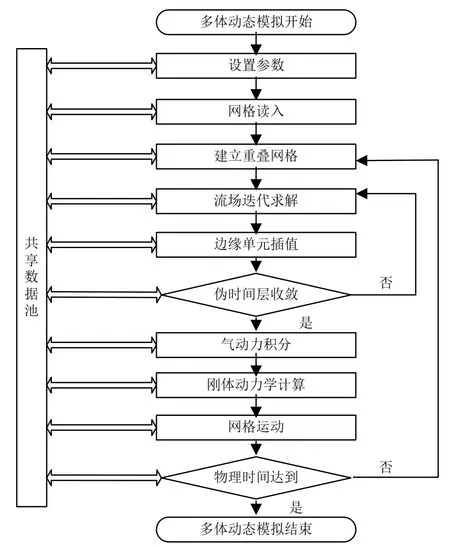
圖3 多體動態問題仿真流程Fig.3 Simulation Flow of Multi-body Dynamic Problem
3 仿真分析
選取飛行器與分離體相對距離最遠、相對速度為零的時刻作為分離體開始側向分離動作的時刻。單個分離體的質量為50 kg,兩分離體各自中心平面間的初始間距為160 mm,初始側向分離速度為25 m/s。
首先依據初始條件進行定常計算,并將其結果作為非定常計算的初場。計算得到的流向截面壓力等值線如圖4所示,對稱面壓力云圖和流線如圖5所示,對稱面馬赫數云圖如圖6所示。
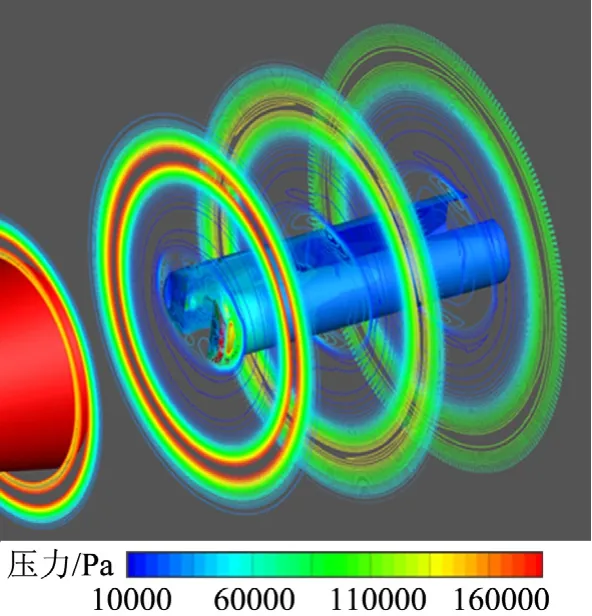
圖4 起始時刻流向截面壓力等值線Fig.4 Pressure Isopleth of Flow Direction Section at the Starting Time
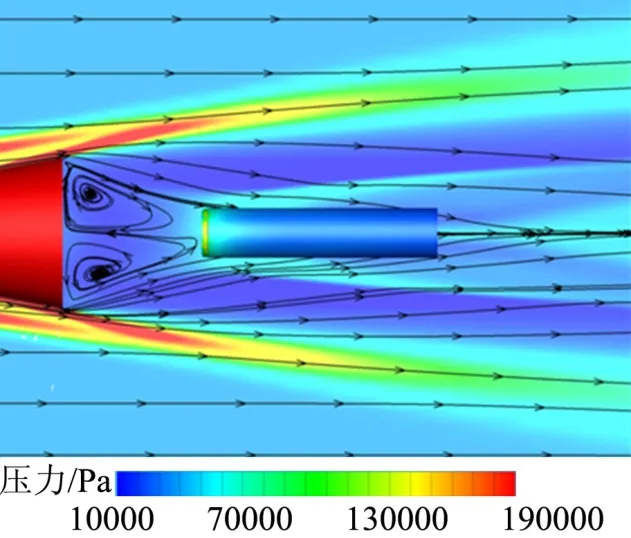
圖5 起始時刻對稱面壓力云圖和流線Fig.5 Pressure Cloud Chart and Streamline of Symmetrical Plane at the Starting Time
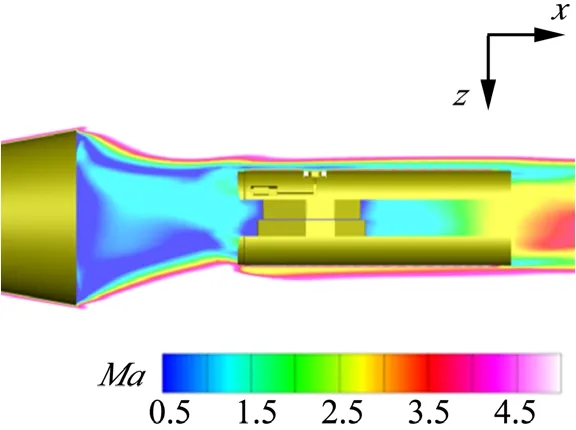
圖6 起始時刻對稱面馬赫數云圖Fig.6 Mach Number Cloud Chart of Symmetrical Plane at The Starting Time
由圖4~6可以看出,在分離體附近存在著復雜的干涉結構,等壓線密集。從對稱面壓力云圖和流線分布可以看到清晰的激波干涉結構,回流區可見兩個較大分離渦。除此之外,在兩個分離體中間區域還存在著若干小分離結構。可知初始時刻分離體完全處在飛行器的底流區中,未脫離底流區干擾。
在定常流場基礎上,開展了非定常分離計算,計算得到的各部件速度和位移曲線分別見圖7、圖8。
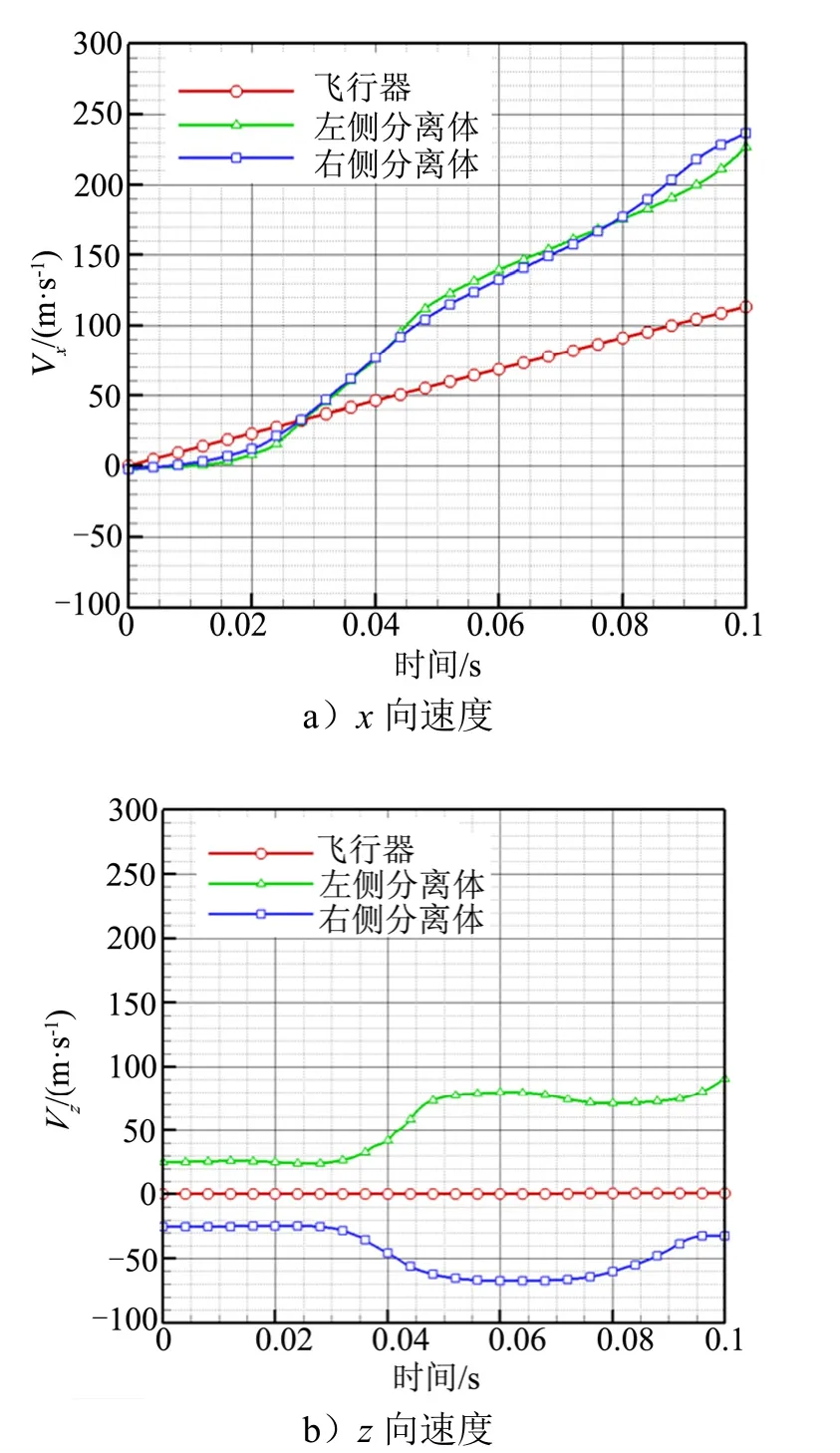
圖7 各部件速度曲線Fig.7 Calculated Variation Curve of Component Centroid Velocity
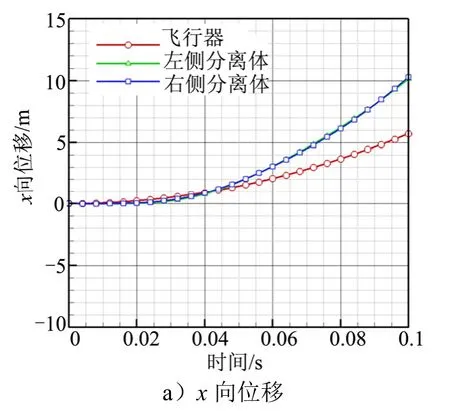
圖8 計算的部件質心位移變化曲線Fig.8 Calculated Variation Curve of Component Centroid Displacement
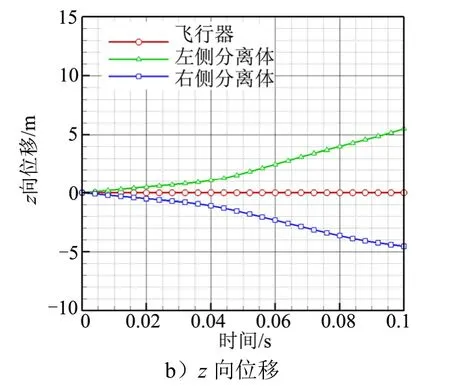
續圖8
由圖8、圖9可以看出,飛行器在氣動力作用下,沿軸向始終呈勻加速運動狀態。左右分離體在0.02 s之前速度幾乎不變,表明其在底流區中受氣動力影響較小,此時段內分離體和飛行器呈相互接近的趨勢。當分離體隨著z向運動接觸到底流區邊界后,開始具有明顯的軸向加速度,在該加速度作用下,其軸向速度開始逐漸增加并超過飛行器的軸向速度,實現了兩者逐漸遠離。計算得到的不同時刻部件相對位置關系見圖9。
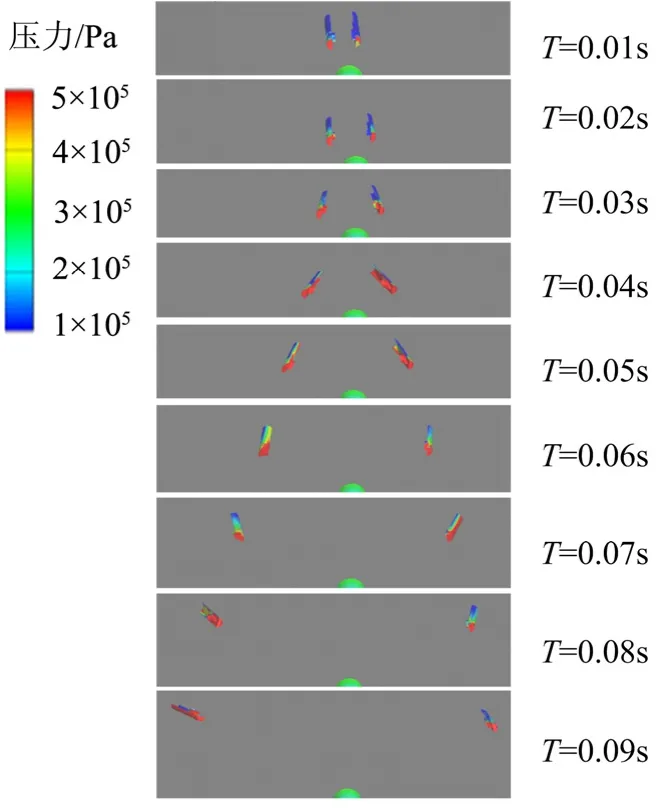
圖9 不同時刻部件相對位置Fig.9 Relative Position of Components at Different Times
由圖9可知,分離體沿側向飛出底流區后,與飛行器在流向上相互遠離,沒有發生回追碰撞。
4 結束語
非定常數值計算結果表明,高超聲速條件下,飛行器底部流場的低動壓環境不利于多體分離方案的實現,通過側拋+后拋的解決方案,可以使分離體沿側向迅速脫離底流區,在較大的來流動壓條件下與飛行器拉開距離,有效避免回追碰撞。

