基于非線性方程組和優化建模的實驗數據重構方法

郝玉潔， 郭子萱， 胡 兵， 唐昌兵， 王浩煜， 辛 勇

(1.四川大學數學學院， 成都 610064； 2.中國核動力研究設計院 核反應堆系統設計技術重點實驗室， 成都 610000)

1 引 言

核反應堆的燃耗深度[1]即單位質量核燃料釋放的核裂變能量，其中乏燃料(即在反應堆中經受過輻射照射的核燃料)的燃耗深度是衡量核電站經濟性和核燃料輻照性能的關鍵指標.測量乏燃料的燃耗深度可通過測量其釋放的γ射線計數[2]來實現.在離散測量γ射線計數過程中，由于受到周圍點的干擾，探測器的讀數并不精準.這會對后續計算帶來誤差和困難.為了克服這個問題，有必要通過建立數學模型、運用數學方法來減小這種探測誤差，重構實驗數據.

在實驗數據的去噪處理中,均值濾波算法[3-4]和中值濾波算法[5-7]是常用的兩種方法，它們對不同的噪聲有不同的去噪特性. 多年來,人們一直致力于改進濾波器,并取得了明顯效果,參見文獻[5，7].近年來，隨著小波理論的發展，很多學者將小波變換應用于信號去噪[8-9].這種方法雖然去噪效果較好，但容易丟失細節信息，導致邊緣模糊.最近，鄧和劉[10]在形態學噪聲濾除器基礎上提出了一種基于形態學成分分析(MCA)和K奇異值分析(K-SVD)的去噪方法，可以一定程度上解決邊緣模糊問題.

在本文考慮的實驗數據重構問題中，誤差源于離散探測點之間的相互干擾，不是服從某種隨機分布的噪聲，因而不能直接應用上述去噪方法，需要建立新的重構模型.本文首先建立了探頭掃描數據的正向計算模型，將工程問題轉化為求解一種不定的非線性方程組[11].該方程組有無窮多個解，需要建立優化問題[12]形式的重構模型，進而求解其特定意義下的最優解.本文建立了兩種重構模型，第一種是根據觀測得到的相對誤差與參數之間的線性關系構造優化目標函數；第二種根據Lagrange乘子法[13-15]建立重構模型.數值實驗結果表明，兩種重構模型得到的重構結果都比探測值更接近真實的精確值，相較而言第二種重構模型的重構結果比第一種更加精確，且具有可以直接把探測值作為迭代初值的優點.

本文結構安排如下：我們在第二節中建立實驗結果正向計算的矩陣模型；第三節分別基于優化目標函數和Lagrange乘子法建立兩種重構模型；第四節通過數值實驗對重構效果進行驗證；第五節總結本文的工作.

本文考慮的離散測量γ射線計數實驗場景如下：被探測物體為一塊矩形板，探測器從板的正上方進行散點式的掃描探測.假設有n1行n2列共n=n1×n2個探測點，將第i個探測點的真實值記為xi，此點的探測值記為yi.點的排列順序如圖1所示.

基于離散測量γ射線計數的特點[1-2]，我們對探測實驗做以下基本假設：

(i) 探測點行與行之間的距離相同，列與列之間的距離相同，且列距不小于行距;

(ii) 目標點xi周圍的探測點會影響目標點的探測值yi，這種影響與兩點之間的距離負相關，并且距離相同的點的影響因子是相同的；

(iii) 目標點的探測值yi只受到探測點本身xi和探測點左方xi-1,右方xi+1,上方xi-n2,下方xi+n2,左上方xi-n2-1,右上方xi-n2+1,左下方xi-1+n2,右下方xi+1+n2共9個點的影響，所有9個點的影響因子之和為1.

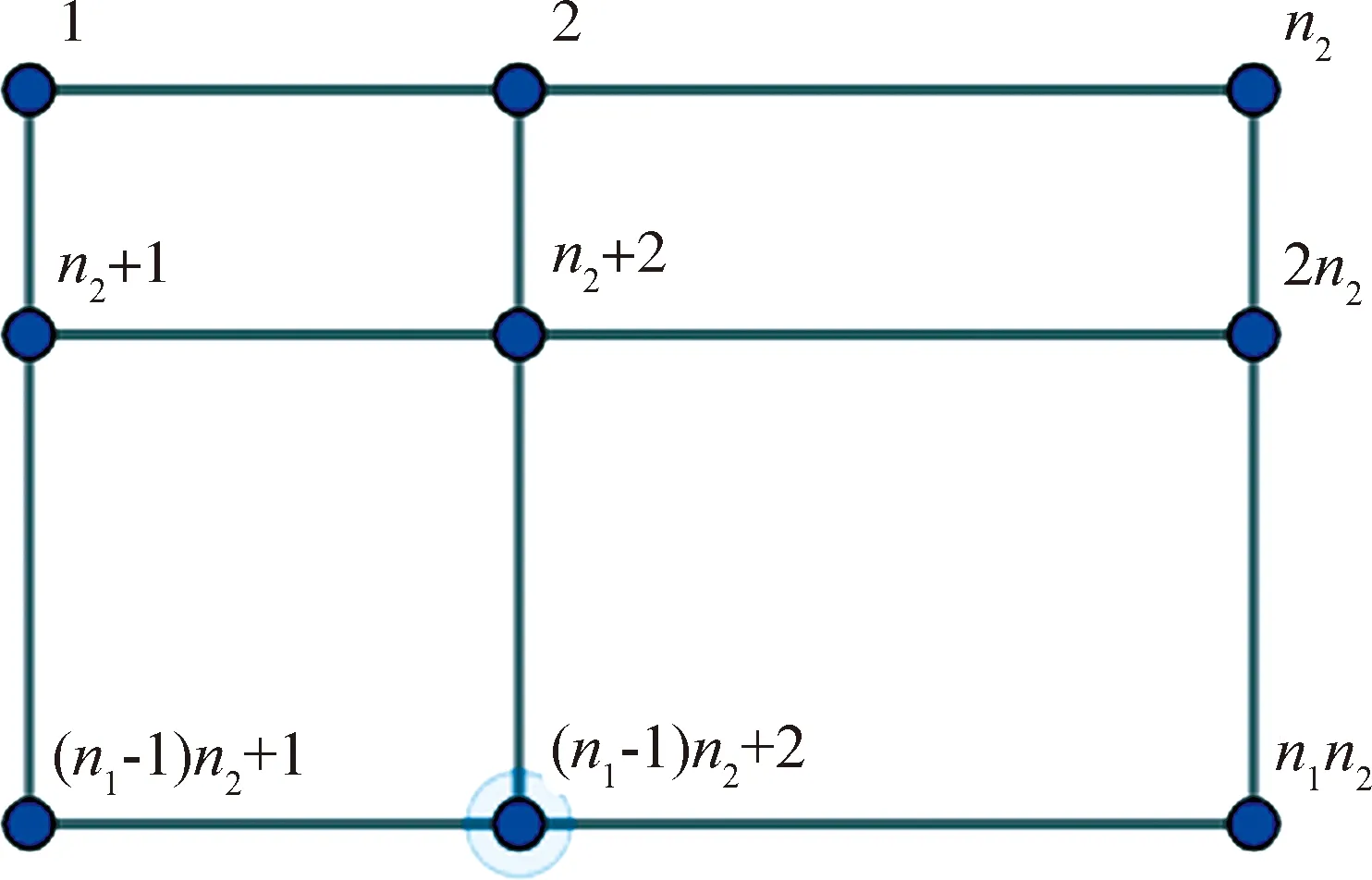
圖1 探測點的順序Fig.1 The order of detective points

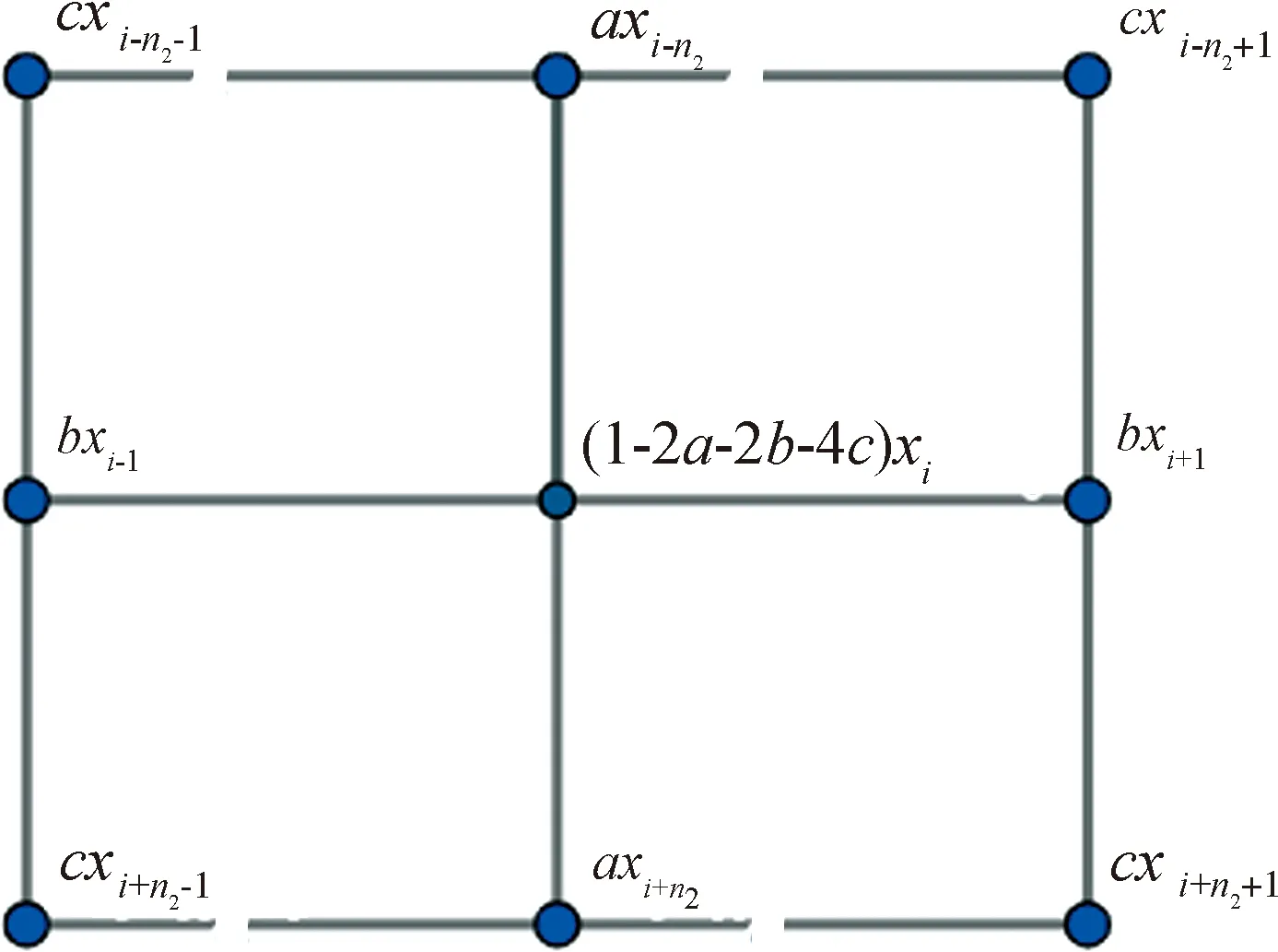
圖2 目標點的探測值可以簡化為附近9個點(包括該點)的真實值的線性組合

根據以上假設，在探測器掃描目標點xi時，探測值yi受到目標點上下兩個點的影響因子是相同的，記為a；探測值受到目標點左右兩個點的影響因子是相同的，記為b；探測值受到掃描點左上，左下，右上，右下四個點的影響因子相同，記為c. 則目標掃描點的影響因子為1-2a-2b-4c.探測值yi為附近9個點真實值的線性組合

yi=(1-2a-2b-4c)xi+

a(xi-n2+xi+n2)+b(xi-1+xi+1)+

c(xi-n2-1+xi-n2+1+xi-1+n2+xi+1+n2)

(1)

根據假設(ii),距離目標點越近，影響因子越大，因而參數應滿足a≥b>c>0.

記x=(xi)i=1,2,…,n∈Rn是每一個探測點的真實數據組成的列向量，y=(yi)i=1,2,…,n∈Rn是每個探測點的觀測數據組成的列向量.我們得到矩陣形式的數學模型

A(a,b,c)x=y

(2)

n階方陣A可以寫成如下n1×n1塊的分塊三對角稀疏矩陣

其中C和D都是n2階的三對角稀疏矩陣,

C=a*diag(ones(n2))+

c*diag(ones(n2-1),-1)+

c*diag(ones(n2-1),1),

D=(1-2a-2b-4c)*diag(ones(n2))+

b*diag(ones(n2-1),-1)+

b*diag(ones(n2-1),1).

進一步,對模型矩陣A化簡，將其中的未知參數a、b、c分離出來，以使比較清晰地觀察A與a、b、c的關系.簡單分析后有A=I-(aA1+bA2+cA3)，其中I為n階單位矩陣，A1、A2、A3為n階對稱正定的矩陣.A1、A3可以寫成n1×n1塊的分塊三對角稀疏矩陣，A2可以寫成n1×n1塊的分塊對角稀疏矩陣，

E=2*diag(ones(n2))-

diag(ones(n2-1),-1)-

diag(ones(n2-1),1),

F=-diag(ones(n2-1),-1)-

diag(ones(n2-1),1).

通過前面建立的矩陣模型，我們已經將這個工程問題轉化成如下的數學問題：

Find (x;a,b,c), s.t.A(a,b,c)x=y

(3)

這是一個不定的非線性方程組，有無窮多解. (y;0,0,0)是其中一個解，代表真實值就等于實驗值，與實際實驗中的相互干擾不符.因此我們需要構建出優化問題形式的重構模型，進而尋找符合實際需求的非(y;0,0,0)的最優解.

3.1 重構模型Ⅰ

由于y=x-(aA1+bA2+cA3)x,則

‖x-y‖2=‖(aA1+bA2+cA3)x‖2，

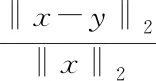
(4)

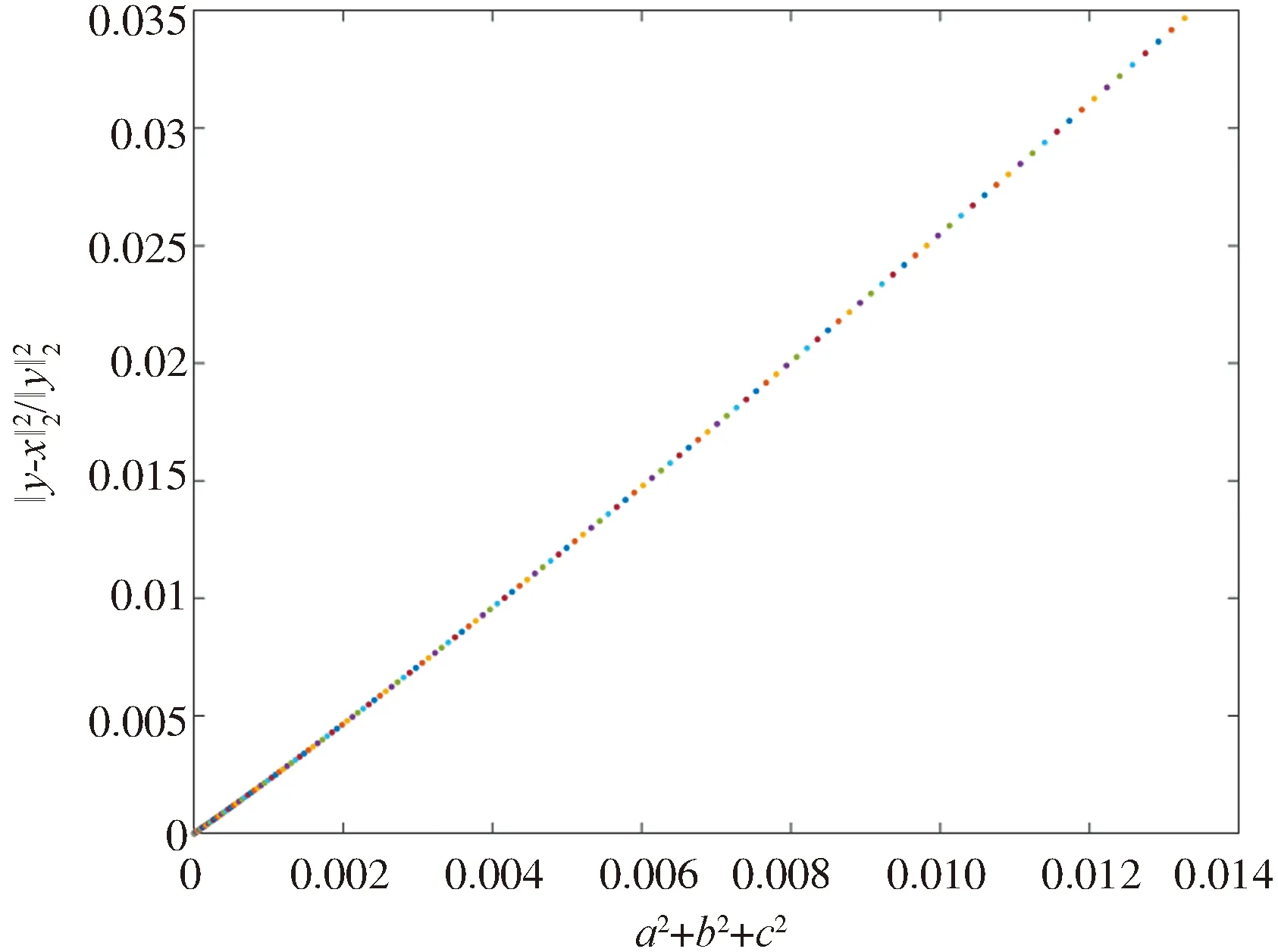
圖與a2+b2+c2的比值Fig.3 The ratio of and a2+b2+c2

s.t.Ax=y,a≥b>c>0

(5)

在上述模型中，參數k需要事先確定.研究人員可以根據探測場景和自己的經驗選取合適的參數值.如果能夠利用工程手段得到若干組探測數據y和精確數據x，根據已有的若干組參考數據x和y，用最小二乘法擬合

可以訓練得到最優的模型參數k.

利用數據通過最小二乘訓練得到參數k時，優化函數在[x;a,b,c]處的取值并不能保證嚴格為0，但在[y;0,0,0]處是嚴格為0的，并且為目標函數的一個全局最小值點.所以，如果將[y;0,0,0]作為初值，那么程序并不會迭代.為了克服這個問題，我們考慮給y加上一個小擾動t，即將[y+t;0,0,0]作為初值.

3.2 重構模型Ⅱ

第一種模型的構造思路非常簡單直接，但它不能將實驗數據[y;0,0,0]直接作為重構模型求解的迭代初值，而我們真正關心的是最終重構結果，a，b，c只是引入的中間變量.為此我們基于Lagrange乘子法建立第二種重構模型.

由于我們只有一個等式約束

x-(aA1+bA2+cA3)x=y

(6)

受Lagrange乘子法的啟發，我們可以將其視為KKT條件：

?xL(x;a,b,c)=

x-y-aA1x-bA2x-cA3x=0

(7)

于是有Lagrange乘子函數

(8)

其中K為常數.對于乘子為a，b，c的拉格朗日乘子函數可以構造很多種優化問題，我們選擇如下的最簡單形式：

(9)

則根據KKT條件，優化問題(9)的解一定滿足式(3).

關于模型參數ki(i=1,2,3)的選取，我們有以下定理.

定理3.1若(x*;a*,b*,c*)是問題(9)的解，且a*,b*,c*均為正數，則

證明 若(x*;a*,b*,c*)是問題(9)的解，則(x*;a*,b*,c*)滿足以下KKT條件.

(10)

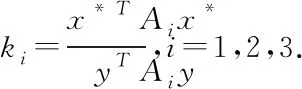
上述定理告訴我們k1，k2，k3的理論選取方式，但由于x*是重構模型需要求解的未知向量，所以這三個參數需要在求解重構模型之前用其他方式選定.類似于重構模型Ⅰ，研究人員可以根據探測場景和自己的經驗選取合適的參數ki.如果能夠借助工程手段得到若干組探測數據y和精確數據x，我們還可以根據這已有的若干組參考數據x和y，使用最小二乘法擬合xTAix-kiyTAiy=0訓練得到模型參數k1，k2，k3.

4 數值算例

本節中我們通過數值實驗來檢驗上述兩種重構模型的效果.基于離散測量γ射線計數的一般規律，我們首先按以下方式隨機生成50組模擬數據x：矩形板上離散探測點最外一圈的取值位于區間[40，100]，再往內一圈數值位于區間[100，200]，再往內圈數值位于區間[500，600].

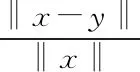
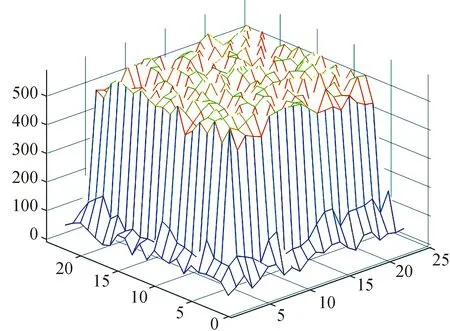
圖4 一組x數據的大致形狀

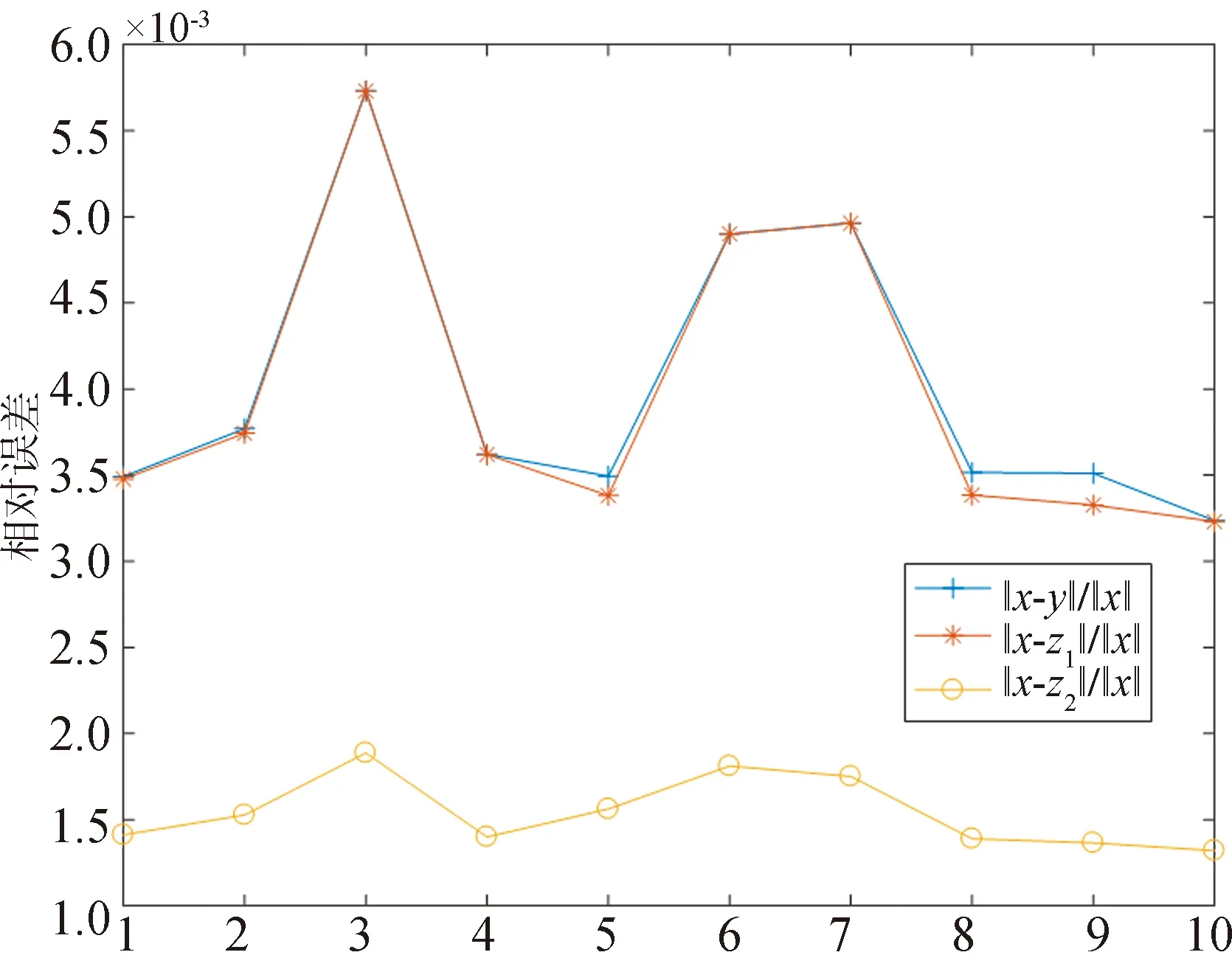
圖5 兩種重構方法的相對誤差及其與探測值的相對誤差

經過最小二乘訓練，得到此次實驗中重構模型Ⅰ的參數為k=0.188 826 971,重構模型Ⅱ的參數為k1=1.030 744 286,k2=1.024 777 026，k3=1.025 237 126.重構效果見圖5.可以看出，兩種重構方法都有效，而第二種重構方法效果比第一種更好.

5 結 論

針對離散測量γ射線計數中的實驗數據重構問題，本文建立了探頭掃描數據的正向計算模型.通過將工程問題轉化為求解一種不定的非線性方程組的數學問題，本文針對此種非線性方程組建立兩種優化問題形式的重構模型.數值實驗結果表明，兩種模型得到的重構結果都比探測器的探測值更接近真實的精確值，相比較而言第二種模型的重構結果比第一種更加精確，且允許直接把探測值作為迭代初值.

在一般的離散掃描實驗中，離散探測點之間都存在局部的相互干擾，干擾方式可以被本文的正向計算模型近似.所以本文建立的重構方法，也適用于大多數領域的離散掃描實驗數據重構，具有廣泛的適用性和工程實用價值.