基于AT的鍋爐燃燒溫度場重建算法研究

武鈺暉， 楊嵐斐， 趙 麗， 周新志

(1. 四川大學電子信息學院， 成都 610065； 2. 成都萬江港利科技股份有限公司， 成都 610043)

1 引 言

在鍋爐運行中，爐膛溫度分布直接影響煤粉的燃燒效率以及鍋爐燃燒安全，是反映燃燒過程及排放物演變的重要參數(shù)[1-2]. 通過了解爐膛溫度場，能適時調(diào)整燃料的混合比例，使設(shè)備處于最佳運行狀態(tài)；有利于提高燃燒效率，減少污染；有助于檢測可能引起爆炸等安全事故的熱點，避免燃燒的潛在隱患. 由于鍋爐燃燒過程中具有環(huán)境惡劣、瞬態(tài)變化等特征，傳統(tǒng)的接觸式測溫難以獲得準確的爐內(nèi)溫度場[3]. 聲學層析成像(Acoustic Tomography, AT)測溫技術(shù)作為一種非侵入式測溫，具有時延小，測量范圍大，環(huán)境適應能力強等優(yōu)點[4-6]，能夠?qū)崿F(xiàn)鍋爐溫度場的實時監(jiān)控，保證燃燒優(yōu)化運行.

AT溫度場重建技術(shù)通過測量超聲波在待測區(qū)域中多條路徑上的飛行時間，結(jié)合重建算法反演出待測區(qū)域的溫度分布情況. 常見的重建算法有最小二乘法(Least Square Method, LSM)，代數(shù)重建法(Algebraic Reconstruction Technique, ART)，基于RBF神經(jīng)網(wǎng)絡的方法以及截斷奇異值分解法(Truncated Singular Value Decomposition Method, TSVD)等. LSM方法[6-10]是目前廣泛用于聲學溫度場測量的一種典型重建算法，計算過程較為簡便，穩(wěn)定性強，能保證較高重建精度，但是最小二乘法重建出的溫度信息數(shù)據(jù)有限，且重建結(jié)果具有邊緣缺失效應. ART[1,3,11]的優(yōu)勢在于原理復雜性相對較低，但結(jié)果易受噪聲干擾. 基于RBF神經(jīng)網(wǎng)絡的方法[12-13]具有任意精度的最優(yōu)泛函逼近能力，但是需要大量可靠的訓練樣本來計算合適的參數(shù)，實用性受到很大限制. TSVD[14]是將造成解不穩(wěn)定的較小奇異值直接截去，但是應截斷多大的奇異值是一個難題. 在最小二乘法的基礎(chǔ)上，顏華等[15]利用Kriging模型同時具有局部和全局的統(tǒng)計特性，在用最小二乘法重建出少量像素后運用克里金法對其進行內(nèi)插和外推運算，從而得到整個區(qū)域的溫度描述. Shen等[2]利用多二次插值處理稀疏數(shù)據(jù)的良好能力，提出一種基于LSM和多二次插值的重構(gòu)算法，使得重建結(jié)果不會在區(qū)域邊緣丟失信息. Jia等[16]將LSM具有較高穩(wěn)定性和精度的優(yōu)點與徑向基函數(shù)數(shù)學擬合的優(yōu)點綜合考慮，研究了一種基于LSM和徑向基逼近的改進重構(gòu)算法，但是徑向基函數(shù)的形狀參數(shù)需要數(shù)值實驗進行合理確定. 因此，如何提高溫度場重建精度，改善重建質(zhì)量依然是一個開放性的問題.

為了提高AT測溫重建精度，改善重建質(zhì)量，本文通過建立基于待測燃燒區(qū)域劃分單元塊的溫度描述得到稀疏網(wǎng)格溫度場，在此基礎(chǔ)上，為了重建出細致的溫度場分布，對網(wǎng)格進一步細化，建立細密網(wǎng)格溫度場模型，并對重建過程的關(guān)鍵參數(shù)進行優(yōu)化整定，最終實現(xiàn)燃燒溫度場的高精度重建.

AT重建溫度場的基本原理是超聲波在介質(zhì)中的飛行速度會隨介質(zhì)溫度的變化而變化，超聲波傳播速度與介質(zhì)溫度的平方根呈正比例關(guān)系[16]，超聲速度和氣體溫度之間的關(guān)系可用下式表示

(1)

其中，v表示氣體中超聲波傳播速度，單位：m/s；γ表示氣體絕熱指數(shù)；R表示理想氣體普適常數(shù)，單位：J/(mol·K)；M表示氣體的摩爾質(zhì)量，單位：kg/ mol；T表示氣體熱力學溫度，單位：K.對于確定的氣體介質(zhì)，M、γ和R均為已知量，則P為一固定可知的常數(shù).若介質(zhì)為空氣，P=20.03[16].

當氣體介質(zhì)和超聲波傳播速度v已知，T表示為

(2)

超聲波收發(fā)傳感器之間的路徑長度是固定的已知常數(shù)，測定二者間的超聲波飛行時間，則可以確定超聲波在傳播路徑上的平均速度.從而取得在待測路徑上的平均溫度，如下式

(3)

其中，L是超聲波收發(fā)傳感器之間的路徑長度；t是傳感器之間的超聲波飛行時間.

利用超聲波對溫度場進行重建要在待測區(qū)域布置多組超聲波收發(fā)傳感器，選取多條他們之間形成的超聲波傳播路徑，測出超聲波的飛行時間，結(jié)合合適的溫度場重建算法，計算出待測區(qū)域的超聲波聲速分布，最后由聲速和溫度的關(guān)系求得待測區(qū)域的溫度分布情況.

3 溫度場重建算法原理

本文提出的重建算法是一種層層遞進的重建算法. 第一層，建立溫度場的稀疏網(wǎng)格模型. 將溫度場待測區(qū)域劃分為稀疏的網(wǎng)格，根據(jù)超聲波飛行時間，采用LSM方法得到待測區(qū)域的稀疏網(wǎng)格溫度場.第二層，建立溫度場的細密網(wǎng)格模型. 在稀疏網(wǎng)格溫度信息的基礎(chǔ)上，將溫度場待測區(qū)域進一步細分. 基于最小二乘支持向量機(Least Squares Support Vector Machine, LSSVM)能實現(xiàn)小樣本的預測且擅長處理復雜的非線性問題的特點[17]，利用訓練好的LSSVM建立待測區(qū)域細化后網(wǎng)格的溫度描述，從而重建出整個待測區(qū)域的溫度場.第三層，重建過程關(guān)鍵參數(shù)的整定. LSSVM重建模型參數(shù)會影響溫度場重建精度，為了從細密網(wǎng)格溫度描述中選出重建精度最高的結(jié)果，再利用優(yōu)化算法對LSSVM模型參數(shù)進行整定，從中找出重建精度最高的模型，從而實現(xiàn)溫度場的高精度重建(本文提出的算法簡稱為LLD算法). 其算法思想概括如圖1所示.

圖1 LLD溫度場重建算法思想

3.1 稀疏網(wǎng)格溫度矩陣的表征

LLD重建算法重建溫度場首先建立稀疏網(wǎng)格，通過LSM方法求解稀疏網(wǎng)格的溫度描述. 結(jié)合距離公式，聲學信號沿著特定的路徑從發(fā)射傳感器到接收傳感器之間的飛行時間(Time of flight, TOF)可表示為

(4)

其中，t為超聲波飛行時間；v為超聲波傳播速度；a是超聲波速度的倒數(shù)；s是超聲波傳播路徑方程.

在溫度場重建中，將待測溫度場平面劃分成N個網(wǎng)格單元塊，由于最小二乘法病態(tài)矩陣求解特性的限制，劃分的單元塊數(shù)N要小于選取的傳播路徑數(shù)M[2,18].設(shè)超聲波的傳播速度在各單元塊內(nèi)是均勻分布的，根據(jù)式(4)，超聲波在第k條選取路徑上對應的超聲波飛行時間可以表達為

(5)

其中，ai表示第i個單元塊中的超聲波平均速度的倒數(shù)；ΔSki表示第k條選取路徑相應通過的第i個單元塊內(nèi)的長度.

(6)

應用最小二乘法，令下式成立.

(7)

可得到正則方程

ST·S·A=ST·t

(8)

其中，

由式(8)可得

A=(STS)-1STt

(9)

根據(jù)式(2)可得

(10)

則T=[T1T2…TN]T為N個網(wǎng)格單元塊的平均溫度組成的矩陣，即得到了稀疏網(wǎng)格中心點的溫度信息，也就是作為LSSVM溫度采樣點的溫度.

3.2 最小二乘支持向量機重建模型

在稀疏網(wǎng)格溫度信息的基礎(chǔ)上，進一步將溫度場網(wǎng)格細化，利用LSSVM建立待測區(qū)域細密網(wǎng)格的溫度描述. LSSVM是一種對標準支持向量機(Support Vector Machine，SVM)的改進算法，相較于SVM，該算法將不等式約束轉(zhuǎn)化為等式約束，采用最小二乘線性系統(tǒng)作為損失函數(shù)，將SVM的二次規(guī)劃問題的求解轉(zhuǎn)化為線性方程組的求解，使得計算進一步簡化[17,19-20]. LSSVM方法具有良好的泛化能力，可以實現(xiàn)樣本數(shù)據(jù)較少的預測，且擅長處理復雜的非線性問題. 該方法的基本原理表述如下.

f(x)=ωTφ(x)+b

(11)

其中，ω表示權(quán)重向量；φ(·)表示非線性變換映射函數(shù)；b表示偏置向量.

則LSSVM的優(yōu)化問題用下式表示

(12)

其中，J(ω)為優(yōu)化的目標函數(shù)；C為正則化參數(shù)，是一個常量；ξi為樣本誤差向量.

為求解方程(12)，引入拉格朗日乘子αi，可將約束最優(yōu)化問題轉(zhuǎn)化為如下的無約束最優(yōu)化問題，得到的函數(shù)表達式如下：

L(ω,b,ξ,α)=J(ω,ξ)-

(13)

根據(jù)Karush-Khun-Tucker(KKT)條件，其最優(yōu)解滿足下式.

(14)

由式(14)則得到求解α和b的線性方程組如下.

(15)

其中，EN=[1;1;…;1]T；α=[α1;α2;…;αN]T；Y=[y1;y2;…;yN]T；IN為單位矩陣；K(xi,xj)為核函數(shù)；Ωi,j=φT(xi)·φ(xj)=K(xi,xj).

則最終得到的LSSVM回歸函數(shù)為

(16)

本文使用徑向基核函數(shù)，表達式如式(17)所示，其中，σ為核寬度.

(17)

3.3 LSSVM重建模型參數(shù)的整定

LSSVM重建模型中正則化參數(shù)C和核寬度σ參數(shù)取值不同，則重建出的細密網(wǎng)格溫度場不同，其精度亦隨之不同. 為了進一步提高溫度場重建的精度，可以取多組LSSVM模型參數(shù)進行預測，得到多個細密網(wǎng)格溫度場，從而在得到的細密網(wǎng)格溫度描述中選出重建精度最高的一種. 為了在可接受的計算成本內(nèi)智能地確定，節(jié)約人力和時間成本，我們結(jié)合優(yōu)化算法實現(xiàn)LSSVM重建模型參數(shù)的整定，從而得到高精度的重建結(jié)果. 本文采用差分進化算法對其進行優(yōu)化. 差分進化算法[22-25](Differential Evolution, DE)是一種基于群體的啟發(fā)式隨機搜索算法，可以通過種群內(nèi)個體之間的合作與競爭智能產(chǎn)生優(yōu)化搜索. 相較于其他優(yōu)化算法，DE算法具有參數(shù)少、算法穩(wěn)定、具有較強的全局尋優(yōu)能力等優(yōu)點.

在溫度場重建中，重建結(jié)果的均方根誤差的大小是評判溫度場重建效果的好壞的常用指標.因此本文以重建結(jié)果的均方根誤差作為求適應度的評價指標. 在DE算法中，首先初始化種群規(guī)模、最大迭代次數(shù)、變異因子、交叉因子等參數(shù)，隨機生成初始種群，而后對種群進行評價，計算種群內(nèi)每個個體的適應度. 之后經(jīng)過變異、交叉和選擇，通過不斷的迭代計算，保留優(yōu)勝個體，逐步尋找到最優(yōu)的參數(shù)，從而實現(xiàn)高精度的溫度分布重建. 同時，為了提高DE算法的快速收斂性和魯棒性，在算法的進化過程自動調(diào)節(jié)變異因子F和交叉因子CR，使得在迭代早期過程中全局搜索能力較強，迭代后期過程中保證計算精度和收斂速度[25]，如下式.

(18)

(19)

其中，g是當前進化代數(shù)；G是最大進化代數(shù)；Fmax、Fmin分別為變異因子最大值和最小值；CRmax、CRmin分別為交叉因子最大值和最小值.

DE算法優(yōu)化LSSVM參數(shù)的具體步驟如下.

(1) 初始化DE的各種參數(shù)：種群規(guī)模、最大迭代次數(shù)、變異因子和交叉因子等.

(2) 隨機初始化一個種群.

(3) 對種群進行評價，計算種群內(nèi)每個個體的適應度. 即分別對每個個體采用LSSVM進行重建，得到每個個體的重建誤差，并將其作為各個體的適應度值.

(4) 按照變異策略進行變異操作，按照交叉策略進行交叉操作，得到新的臨時種群.

(5) 對臨時種群進行評價，計算臨時種群中每個個體相應的適應度值；進行選擇操作，得到新種群，綜合得到適應度最佳的個體.

(6) 判斷是否滿足迭代次數(shù)，若滿足輸出此時的最優(yōu)個體即最優(yōu)解，否則，返回步驟(4).

4 仿真實驗與結(jié)果分析

4.1 仿真實驗與結(jié)果

為了評估算法的可行性和有效性，利用LLD算法對東方鍋爐廠提供的爐溫分布在MATLAB平臺上進行重建實驗.

溫度場待測區(qū)域的尺寸為25 m×8.22 m，即鍋爐測溫區(qū)域的實際長度和寬度. 如圖2所示，將該區(qū)域劃分為5×3個網(wǎng)格單元塊，其中T1～T10表示均勻布置在待測區(qū)域四條邊上的10個收發(fā)一體的超聲波傳感器，共形成23條有效的超聲波傳播路徑. 東方鍋爐廠提供的三種溫度場分布如圖3所示，分別為單峰溫度場、雙峰溫度場和高低峰溫度場.

圖2 超聲波收發(fā)傳感器的布局及待測區(qū)域劃分情況

仿真時，DE算法的種群規(guī)模設(shè)為20，最大迭代次數(shù)為200次，變異因子Fmax、Fmin分別為0.9和0.2，交叉因子CRmax、CRmin分別為0.6和0.1，變異策略選用DE/rand/1變異策略，交叉策略選用二項式交叉策略. 將LLD算法重建結(jié)果與以下幾個算法進行比較：最小二乘法LSM[6]，基于最小二乘法和三次樣條插值的算法(Algorithm based on LSM and Cubic Spline Interpolation, LSM-SP)[7]，基于代數(shù)重建法和三次樣條插值的算法(Algorithm based on ART and Cubic Spline Interpolation, ART-SP)[3]，基于最小二乘法和克里金插值的算法(Algorithm based on LSM and Kriging Interpolation, LSM-KR)[15]，基于最小二乘法和多二次插值的算法(Algorithm based on LSM and Multiquadric Radial Basis Function Interpolation, LSM-MQ)[2]. 其中，最小二乘法采用常用的雙立方插值(Bicubic Interpolation, BI). 圖4～圖6分別展示了以不同算法實現(xiàn)的三種溫度場重建結(jié)果.

(a) 單峰溫度場(a) Single-peak temperature field

(b) 雙峰溫度場(b) Double-peak temperature field

(c) 高低峰溫度場(c) High-low peak temperature field

(a) LSM-BI

(b) LSM-SP

(c) ART-SP

(d) LSM-KR

(e) LSM-MQ

(f) LLD

(a) LSM-BI

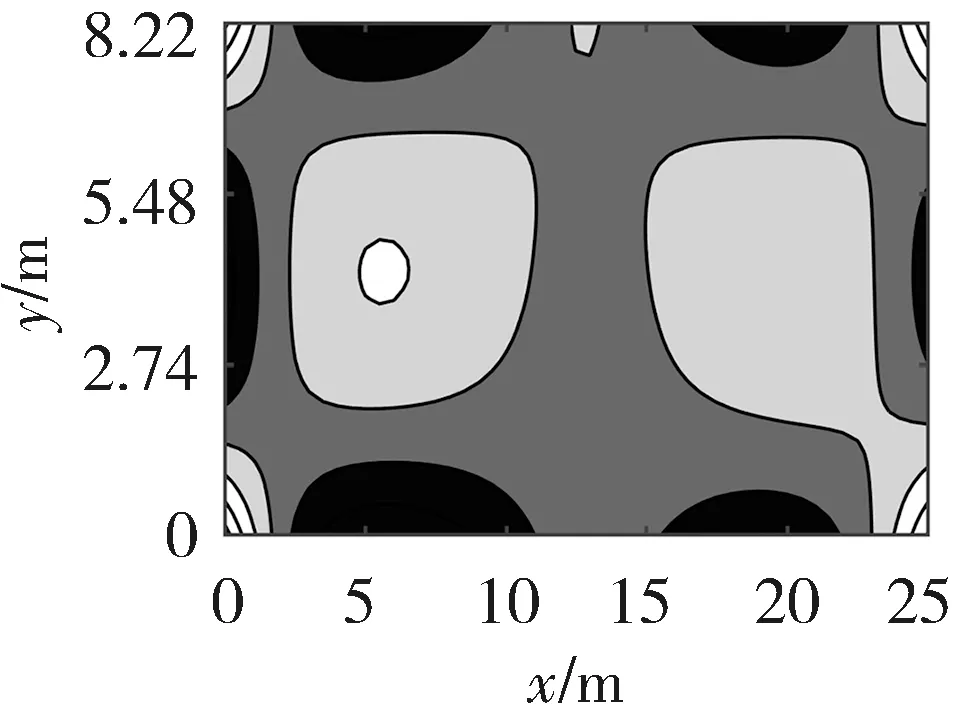
(b) LSM-SP

(c) ART-SP

(d) LSM-KR

(e) LSM-MQ

(f) LLD

(a)LSM-BI

(b) LSM-SP

(c) ART-SP

(d) LSM-KR

(e) LSM-MQ

(f) LLD

從圖4～圖6可以看出，LLD算法可以有效地對溫度場進行重建. 這6種算法都可以描述溫度場的分布信息，但是LSM算法在溫度場的邊緣存在信息丟失的不足，與另外5種算法相比，LLD算法的溫度場重建質(zhì)量較高.

4.2 誤差分析

為了定量評估各種算法的溫度場重建效果，本文使用了兩種誤差評價標準——平均絕對誤差以及均方根誤差，誤差函數(shù)定義如下.

(20)

(21)

其中，n為重建出的溫度值數(shù)目；TRi和TMi分別代表算法所得重建結(jié)果與東方鍋爐廠提供的模擬溫度場在同一坐標下對應的溫度值；TMmean為模擬溫度場的平均溫度.

為了全面分析溫度場的重建效果，本文除了從全局分析重建誤差外，另外從中心區(qū)域和邊緣區(qū)域兩個區(qū)域有針對性地對重建誤差進行分析對比. 其中，中心區(qū)域即最小二乘法和雙立方插值能重建出來的部分，邊緣區(qū)域即待測溫度場除中心區(qū)域外的部分. 對于LSM-BI算法，由于邊緣溫度信息缺失，中心區(qū)域的誤差看作全局誤差. 三種溫度場重建結(jié)果的全局誤差、中心區(qū)域誤差和邊緣區(qū)域誤差如表1～表3所示.

表1 單峰溫度場重建誤差

表2 雙峰溫度場重建誤差

表3 高低峰溫度場重建誤差

表1表明對于單峰溫度場，從中心區(qū)域誤差和邊緣區(qū)域誤差來看，LLD算法重建結(jié)果的平均絕對誤差和均方根誤差均小于其他比較重建算法. 從全局的誤差來看，由于LSM算法的溫度場重建具有邊緣缺失，故不進入全局誤差的對比. 與其他比較算法相比，LLD算法的重建誤差最小，重建效果最好. 從表2可以看出，對于雙峰溫度場，LSM-SP算法和ART-SP算法的重建誤差較大. 從全局來看，LLD算法重建結(jié)果的均方根誤差相較于其他比較算法中的最小值降低了2.1%. 由表3可知，對于高低峰溫度場，LLD算法重建結(jié)果在中心區(qū)域和邊緣區(qū)域的均方根誤差比所有其他算法中的最小值分別降低了1.26%和0.87%. 從全局來看，LLD算法相較于其他比較算法重建精度最高. 從表1～表3的定量分析中可以看出，相較于其他比較算法，LLD算法無論是對于中心區(qū)域還是對于邊緣區(qū)域，都具有較高的重建質(zhì)量. LLD算法實現(xiàn)了高精度的溫度場重建.

4.3 噪聲對重建結(jié)果的影響

由于超聲波飛行時間在實際測量中會存在一定的誤差，為模擬實際飛行時間測量值，因此在飛行時間理論值上加入了不同水平的噪聲，如下式.

tm=ta×(1+α×Nnoise)

(22)

其中，tm代表測量的超聲波飛行時間數(shù)據(jù)；ta是實際的超聲波飛行時間數(shù)據(jù)；α即代表噪聲水平；Nnoise是標準正態(tài)分布的高斯噪聲. 表4給出了噪聲水平分別為1%，3%，5%下的LLD算法重建結(jié)果誤差.

表4 添加噪聲后的LLD算法重建誤差

表4體現(xiàn)了LLD算法的魯棒性. 同時可看出，隨著噪聲水平的增加，溫度場重建結(jié)果的平均絕對誤差和均方根誤差也都在逐漸增加. 因此超聲波飛行時間的測量精度直接影響溫度場重建效果，精度越高，重建效果越好. 這個結(jié)果表明，在實際測量時，應當盡量降低噪聲干擾，進一步改善超聲波飛行時間數(shù)據(jù)的測量質(zhì)量.

LLD算法通過對燃燒區(qū)域稀疏網(wǎng)格和細密網(wǎng)格溫度場的遞進重建，以及對LSSVM模型關(guān)鍵參數(shù)的優(yōu)化整定，實現(xiàn)了鍋爐燃燒溫度場的高精度重建. 通過對鍋爐廠提供的三種溫度場進行仿真重建實驗，證明LLD算法克服了最小二乘法邊緣溫度信息缺失的問題，能夠?qū)崿F(xiàn)全局重建. 實驗結(jié)果的誤差分析表明，LLD算法的重建誤差優(yōu)于相關(guān)算法，它對中心區(qū)域和邊緣區(qū)域的溫度場重建都具有較佳的重建性能. 因此，LLD算法能夠有效地描述溫度場的信息，實現(xiàn)高精度重建. 考慮到噪聲水平會影響重建結(jié)果的誤差，超聲波飛行時間數(shù)據(jù)的去噪將是今后進一步研究的方向.