基于灰色馬爾可夫模型的廣東省2010—2019年漁業生產事故研究

厚得雨，林 群，黃應邦，任玉清，馬勝偉，張慶男，吳洽兒

（1.大連海洋大學航海與船舶工程學院，遼寧大連 116023；2.中國水產科學研究院南海水產研究所，廣東廣州 510300；3.中國水產科學研究院黃海水產研究所，山東青島 266071；4.農業農村部外海漁業開發重點實驗室，廣東廣州 510300）

漁業面臨比其他行業更高的風險和更嚴重的自然災害［1］。2016年12月，我國已經明確將漁業生產列入8個高危行業之一。船舶種類按照設計用途來分［2］，大致分為漁船、運輸船、工程船舶、港務船、特種船舶和艦艇等。其中，漁業船舶數量占比最大，據船訊網統計，在中國沿海航行的船舶中，漁業船舶的占比達到了45.8%。

廣東省是我國漁業捕撈和水上交通運輸最發達的省份之一，具有漁業資源豐富、漁港泊位密布、水路口岸發達、通航資源豐富、漁船和漁民眾多、商船水路運輸量較大等特點［3］。由于極端天氣和水上交通運輸條件復雜性等因素的影響，漁業船舶水上安全事故時有發生，安全生產形勢嚴峻。

目前，國內外漁業船舶水上事故預測分析的研究較少，僅在數據統計分析方面有一定的研究，例如統計分析險情和事故的各項指標、漁業船舶的種類、漁船事故發生的時間、漁業船舶事故水域分布、漁業船舶的捕撈方式等［4－7］。另外，也有學者利用演繹推理法中的事故樹方法［4－5］進行定量的預測分析，這種方法從“人-機-環境-管理”等方面系統地分析了漁業船舶水上事故的原因，但往往出現不同的分析人員繪制的事故樹不同，而導致分析結果不同的現象，其分析事故原因是強項，預測將要發生的事故數是弱項［8－10］。安全工作的目的就是盡可能地避免和減少事故發生。為了使安全管理工作措施有針對性，就需要對以往的事故進行科學分析，找出事故發生的規律，以便進行預測預報。目前，預測的方法高達150多種，主要分為兩大類：一是定性預測；二是定量預測。王崢等［11］應用多元線性回歸模型對漁業安全生產事故進行了分析。童飛［12］運用BP神經網絡的方法對水上交通事故進行了預測，神經網絡組合模型［13－15］在水上事故的預測方面也得到了廣泛應用。趙佳妮和吳兆麟［16］在水上交通事故預測研究中采用線性預測方法，建立了灰色馬爾科夫預測模型，得到了較好的預測效果。

近年來，人們逐漸意識到事故預測的重要性，有關事故預測方面的研究越來越受關注。由于漁業船舶水上事故是小概率的隨機事件，許多數據屬于保密范疇，樣本數據少，多元線性回歸模型［17］、神經網絡算法［18］等很難應用于漁業船舶水上事故的預測中。

針對廣東省漁業船舶水上事故數據少，本文提出了將灰色馬爾科夫模型應用于漁業船舶水上事故研究的方法。利用廣東省漁船水上交通事故相關歷史數據建立灰色馬爾科夫模型，對漁船事故未來可能發生的狀況進行定量預測，分析未來事故的危險程度和發展趨勢，以便及早采取措施進行預防。研究結果可為漁業主管部門預防漁業船舶水上事故提供依據。

1 研究方法

灰色系統理論是我國華中科技大學鄧聚龍教授于1982年創立的［19］，該方法的顯著特點是能夠以較少的已知信息為基礎，通過一定的處理方法提取原始數據中有價值的信息，并揭示其本質規律，從而預測事物未來的發展趨勢［20］，具有不需要大量樣本、樣本不需規律分布和計算量小等方面的優勢。對于漁業船舶水上事故的樣本數據小、不確定性大等問題，灰色理論模型有著較強的適用性。

1.1 灰色預測模型

①設n年的漁船水上安全事故數作為灰色模型的初始時間序列。

1.2 馬爾科夫過程

馬爾科夫過程是由俄國數學家馬爾科夫（Markov）于1906年提出的，是研究自然科學、工程科學和社會科學各領域中常見隨機現象的一類重要隨機過程。近年來，隨著研究的深入，馬爾科夫過程在計算科學、統計物理學、生物生態學、自動控制、數字計算方法、經濟管理和市場預測、人工智能和人工神經網絡領域得到了廣泛應用［21］。

1.2.1 模型構建

1.2.2 狀態劃分

將灰色GM（1，1）模型得出漁業船舶水上事故的預測值與實際值作差獲得殘差，再用殘差除以真實值得到相對誤差，把相對誤差σ劃分成幾個狀態區間。如果計算得到的相對誤差數據較多，則劃分的區間應適當多一些，相反計算得到的原始數據不多，則劃分的區間應該減少。通常，狀態區間劃分的數目為3～5個。

Ej＝［σ1i，σ2i］，其中：Ej為系統處于第i種狀態，σ1i，σ2i分別是狀態區間內的上下限。

1.2.3 計算狀態轉移概率

狀態轉移概率即為系統在n時刻處于狀態i的條件下，在時刻n＋1系統處于狀態j的概率。相當于隨機游動的質點在時刻n處于狀態i的條件下，下一步轉移到狀態j的概率，記此條件概率為pij（k）。

式（15）中，p11是指數據從區間1轉移到區間1的概率。同理，p12是數據從區間1轉移到區間2的概率。

1.2.4 預測值的計算

確定了系統未來的轉移狀態后，也就確定了預測值的變動區間［σ1i，σ2i］，最可能的預測值可認為是該區間的中點，通過對灰色預測的修正得到灰色馬爾科夫預測值Yk。

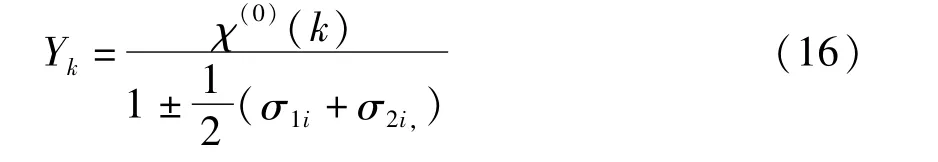
式（16）中，在預測值“高估”時取正號，“低估”時取負號。

2 結果與分析

2.1 漁業船舶事故預測結果

利用灰色馬爾可夫模型對廣東省漁業船舶水上事故進行預測，數據來源于廣東省海洋綜合執法總隊。

①建立灰色GM（1，1）模型

②對10年的漁船事故數進行累加處理，得到新的數據：

表1 2010—2019年廣東省漁業船舶事故數量Tab.1 Number of fishery vessel accidents in Guangdong Province during 2010—2019

χ（1）＝［χ（1）（1），χ（1）（2），…，χ（1）（10）］＝（65，105，157，200，237，275，306，339，360，386）（17）

③對上述序列建立一階線性方程，通過最小二乘法求取灰色參數a和b，得到：

a＝0.078 8，b＝54.965 1

④求得a和b帶入微分方程，得到預測序列：

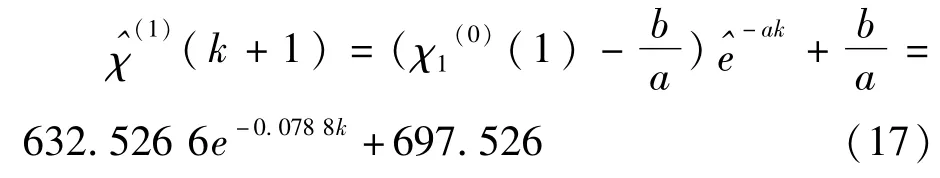
⑤后驗差檢驗：

利用2010—2019年廣東省漁業船舶水上事故數，作為灰色GM（1，1）模型的訓練數據，對漁業船舶水上事故數進行了預測，通過后驗差分析驗證所建灰色GM（1，1）模型是否符合預測精度要求。

基于灰色預測理論模型實現了對廣東省漁業船舶水上事故數的預測，模型檢驗方差比值C＝0.362 6，小誤差概率P＝1，從表2中可以看出，通過灰色預測模型得出了較為符合要求的計算結果。

表2 預測等級對照表Tab.2 Comparison of prediction grades

通過灰色GM（1，1）模型計算得到了廣東省漁業船舶水上事故的預測值與真實值的對比圖（圖1）。

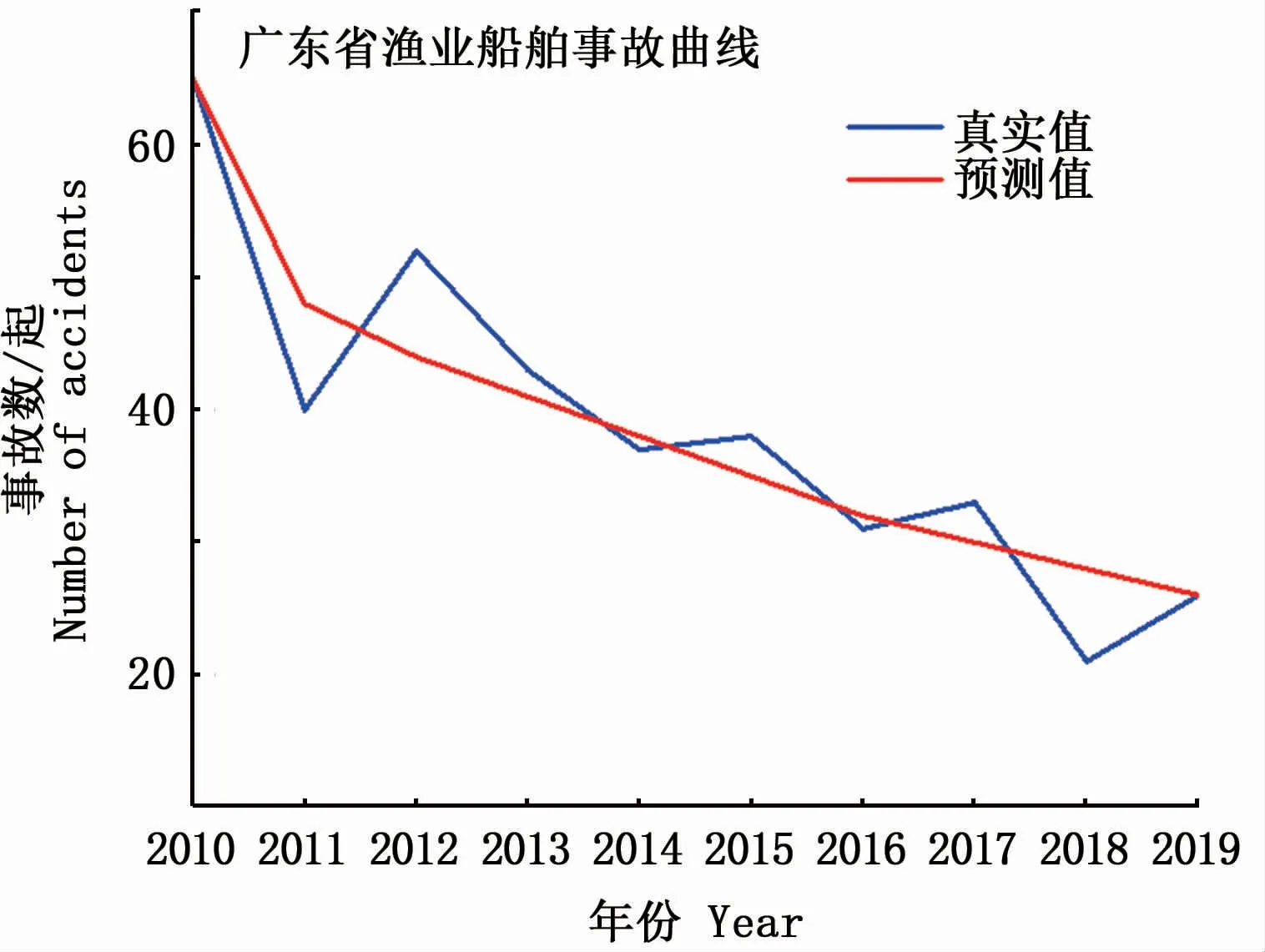
圖1 預測值與真實值對比圖Fig.1 Comparison between predicted and actual number of accidents

2.2 灰色馬爾科夫預測模型

2.2.1 灰色預測相對誤差

計算灰色預測GM（1，1）預測值的相對誤差，如表3所示。灰色預測值與實際值的相對誤差范圍為（－0.33，0.15），考慮到漁業船舶水上事故量少，將各年水上事故劃分成4種狀態，E1＝［－0.33，－0.21］，E2＝［－0.21，－0.09］，E3＝［－0.09，0.03］，E4＝［0.03，0.15］。根據廣東省漁業船舶水上事故灰色預測殘差，計算轉移狀態，如表4所示。

表3 相對誤差對照表Tab.3 Relative error comparison table

由式（14）和（15）計算得到狀態轉移矩陣：

由表4可知，2011年所處狀態為E2，由狀態轉移矩陣可知，狀態E2下一年最可能轉移到狀態E4，則灰色馬爾可夫的預測值為：

表4 狀態劃分Tab.4 State division

Y2表示2011年經過灰色馬爾科夫模型計算所得漁船事故數的預測值。同理，其他年份均采用該方法。

事故預測誤差對比結果如表5所示。可以看出，2010—2019年漁業船舶水上事故灰色預測模型的平均絕對誤差為9.591%，而灰色馬爾科夫預測模型（GM-Markov）的平均絕對誤差為3.388%，由此說明通過對灰色理論GM（1，1）模型與馬爾科夫模型相結合，有效地提高了隨機波動性較高的漁業船舶水上事故的預測精度。

表5 事故預測誤差對比Tab.5 Comparison of accident prediction error

3 結論

本文鑒于漁業船舶水上事故數據少、信息貧的基本情況，提出利用灰色預測模型對廣東省漁業船舶水上事故數進行初步預測，結合馬爾科夫模型進行結果修正，以提升預測精度。結果表明：灰色馬爾科夫模型對漁業船舶水上事故定量預測具有一定的可行性，根據事故統計數據可以運用灰色馬爾科夫模型對漁業船舶水上事故進行定量預測。未來可將各類漁船事故分別運用灰色馬爾科夫模型預測分析，可以使事故防范更有針對性。

（1）通過對灰色預測模型的精度驗證，得到了符合要求的預測結果，但個別年份誤差較大，最大可達33.33%，不能準確反映事故的發展趨勢，需要提高預測的精度。

（2）為了提升預測精度，提出了灰色馬爾科夫模型，將灰色GM（1，1）模型與馬爾科夫模型結合，充分利用歷史數據給予的信息，平均絕對誤差從9.591%降到了3.388%，大大提高了隨機波動性較大的漁業船舶水上事故的預測精度。

（3）漁業船舶水上事故具有隨機性、波動性和不確定性等特點，因此，運用灰色馬爾科夫組合模型綜合考慮，使研究分析結果更加可靠。近年來，漁業生產事故逐步減少，體現了黨中央、國務院和農業農村部對安全生產工作的高度重視，漁業安全生產應強調預防為主，同時提高漁業應急處置能力，堅決防范和遏制重特大事故發生，保障漁民群眾生命財產安全。