太赫茲波在神經細胞中傳輸的弱諧振效應*

郭良浩 王少萌2) 楊利霞 王凱程 馬佳路 周俊 宮玉彬2)?

1) (電子科技大學電子科學與工程學院，成都 610054)

2) (電子科技大學，醫工結合應用醫學研究中心，成都 610054)

3) (電子科技大學物理學院，成都 610054)

神經細胞的尺寸與太赫茲波的波長處于同一數量級，因此，神經細胞可等效為微型介質諧振器從而起到增強細胞內的太赫茲信號的作用.基于此現象，本文提出神經細胞弱諧振效應的新概念.建立了三層結構的球形神經細胞胞體模型，用太赫茲時域光譜儀系統測量了神經細胞生理液的相對介電常數，并用雙德拜模型對實驗結果進行擬合;利用時域有限差分法對太赫茲波在神經細胞中的傳播特性進行研究.結果表明，當神經細胞的相對介電常數高于外部媒質時，太赫茲波可以在神經細胞內部形成弱的諧振峰，并且隨著細胞與外部媒質的相對介電常數差值的減小，諧振峰會向細胞膜側偏移，細胞對太赫茲波的聚焦特性會隨著兩側相對介電常數差值的減小而逐漸增強，這種現象稱為弱諧振效應.同時，弱諧振效應也表現出與細胞尺寸和頻率的相關性.神經細胞的弱諧振效應在增強細胞內太赫茲信號強度的同時，也會進一步增強太赫茲信號在神經纖維中的傳輸.這些結果為解釋太赫茲波與神經細胞的相互作用提供了新模型，有助于研究太赫茲波在生物神經系統中的傳遞機制.

1 引言

神經元是神經系統的基本結構和功能單元，可以感受和傳導興奮.神經元的結構特征主要包括細胞體和突起兩部分，較短的突起稱為樹突，較長的突起成為軸突;軸突與靶細胞相連，實現動作電位在神經元之間的傳導.對于神經軸突而言，其外圍會形成由施萬細胞包裹形成的髓鞘結構，該結構不僅可以加快動作電位的傳導，同時由于髓鞘在太赫茲頻段乃至光學頻段具有較高的折射率，對于特定頻率的太赫茲波和光波可以看作介質波導[1，2].另外，太赫茲生物學和光遺傳學的興起，也激發了眾多學者的思考，生物體中是否存在高頻信號傳導通路，可以實現太赫茲波作為載波的生物體內的信號傳輸?

在光學波段，已有研究表明電磁波在透過生物細胞時，可以發生聚焦現象.2015 年，Miccio 等[3]報道了無核的懸浮紅細胞在光學頻段表現出自適應液體透鏡的特征，并展示了其成像能力和可調諧焦距特性;隨后Johari 等[4，5]證明神經元的體細胞和細胞核同樣具有這種聚焦效應，理論和實驗研究表明，神經元能夠聚焦光的傳輸，使其能夠通過組織傳到目標細胞.細胞的這種現象也被應用于體內光遺傳納米網絡的研究[6-8].在毫米波頻段，有研究表明，具有這種球體以及橢球體結構的生物組織可以增強局部的電磁波傳輸，尤其是當目標樣品的尺寸與電磁波的波長在同一個數量級時，這種相互作用會更加強烈.有研究報道稱，當兩顆葡萄之間存在窄帶隙時，葡萄的高相對介電常數可以在GHz 頻率下產生表面等離子體[9].而在太赫茲波段，神經細胞尺寸與太赫茲波波長都處于微米量級，具備太赫茲波與細胞相互作用的條件，但由于生物體內較高的含水量對太赫茲波的強吸收特性[10]，使得該領域的研究鮮有報道.

基于現有的文獻對神經細胞的特征描述，我們發現了神經細胞在太赫茲波段弱諧振效應的新現象，即尺寸在微米量級的神經元胞體，對太赫茲頻段(波長微米量級)的電磁波傳輸具有增強效應.本文利用時域有限差分法(FDTD)建立了三層結構的神經細胞胞體模型，對太赫茲波在神經細胞中的傳輸特性進行了分析，同時考慮到神經細胞結構的特異性，計算了細胞體-軸突中太赫茲波的傳輸特性，以探索神經元中的太赫茲信號傳輸性能.本研究為構建神經系統中的太赫茲波傳輸提供了一種可能的物理機理闡釋，為實驗工作提供了一種理論預期.

2 研究方法

2.1 神經細胞胞體模型構建

神經元細胞是神經系統最基本的結構和功能單元，根據功能的不同，其形態也有所差異，細胞體的形狀大致分為橢球形、三角形和不規則形狀.鑒于單個神經細胞的相對介電常數難以精確測量，本文建立了包含細胞膜、細胞內生理液以及細胞核的簡化三層結構的球體細胞模型來模擬神經細胞胞體，如圖1 所示.

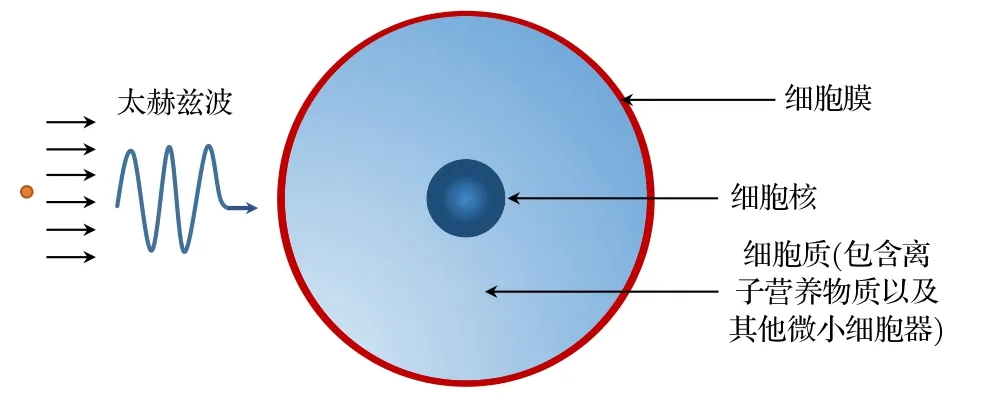
圖1 細胞膜、細胞內生理液和細胞核三層媒質構建的神經細胞體模型Fig.1.Nerve cell body model constructed by three layers of membrane，intracellular fluid and nucleus.

一般細胞膜的結構特點為中間的磷脂雙分子層構成基本骨架，蛋白質分子嵌入在磷脂雙分子層中或表面.而神經細胞膜與一般細胞膜不同之處是膜表面分布著大量的離子通道和特異性受體，能夠感受和傳導興奮.由于神經細胞膜組分的復雜性以及提取制備過程中難以保證其完整的結構功能，本文采用細胞膜的主要組分磷脂的相對介電常數來表征神經細胞膜的相對介電常數.磷脂在太赫茲頻段的相對介電常數可以由文獻[11]得到，通過二階德拜模型擬合后，德拜參數如表1 所列.細胞內生理液的相對介電常數本文通過實驗測量得到.

表1 細胞膜二階德拜模型參數擬合結果Table 1. Fitting results of membrane second-order Debye model parameters.

由于細胞核內的溶劑分子與細胞質中的相同，在太赫茲波在神經元細胞中傳輸過程的模擬計算中，采用細胞內生理液的相對介電常數來代表細胞核的相對介電常數.另外，由于線粒體等細胞器半徑為1 μm 左右，遠遠小于廣義太赫茲波的波長(3—100 μm)，太赫茲波經過微小細胞器時，只表現為衍射和繞射行為，因此計算中也忽略了其影響.

2.2 細胞內生理液的相對介電常數的測量

細胞內生理液由非極性鹽離子和營養物質組成，在神經細胞中起著重要作用.采用太赫茲時域光譜儀(THz-TDS)系統(Tera View TPS 3000)測量細胞內生理液體在生理濃度下的太赫茲光譜[12]，實驗環境為一個大氣壓，溫度為292 K.通過實驗配制得到等效的神經細胞生理液:KCl (1.043 g/100 mL)，MgCl2·6H2O (0.041 g/100 mL)，CaCl2(0.011 g/100 mL)，Na2ATP (0.11 g/100 mL)，EGTA(0.38 g/100 mL)，HEPES (0.238 g/100 mL)[13].在測量過程中，樣品溶液被注入兩個材料為聚四氟乙烯的太赫茲窗片之間，窗片對太赫茲波的吸收可以忽略.在0.3—2 THz 的頻率范圍內，細胞內生理液體的折射率以及吸收系數的測量結果如圖2(a)和圖2(b)所示.

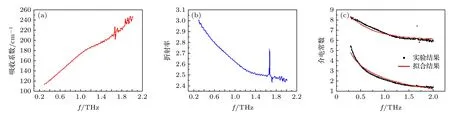
圖2 等效細胞內生理液體在0.3-2 THz 頻率范圍內的(a) 吸收系數，(b)折射率，(c)相對介電常數實部和虛部(黑色圓點)以及二階德拜模型擬合結果(紅色實線)Fig.2.(a) Absorption coefficient，(b) refractive index，and (c) the real and imaginary parts of the dielectric constant of the effective intracellular fluid in the frequency range of 0.3-2 THz.

利用實驗測量得到的折射率以及吸收系數，采用(1)式與(2)式計算可以得到神經細胞內生理液在0.3—2 THz 頻率范圍內的相對介電常數.

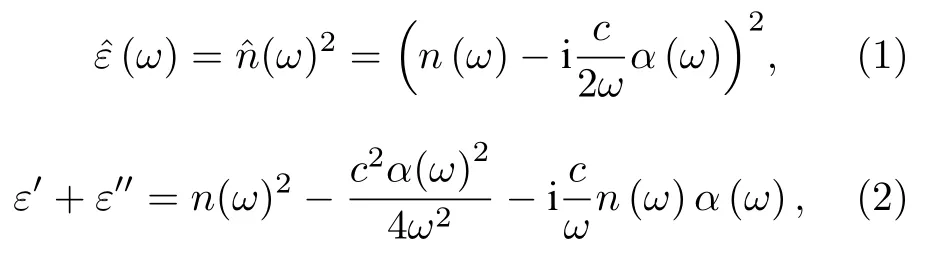
式中，為復折射率，n為折射率，α為吸收系數，c為光速，ω為頻率，為復相對介電常數，ε′為相對介電常數實部，ε′′為相對介電常數虛部.對于神經細胞內生理液在0.3—2 THz 頻率范圍的相對介電常數，可以采用二階德拜模型[14]對實驗測得的相對介電常數進行擬合求得:

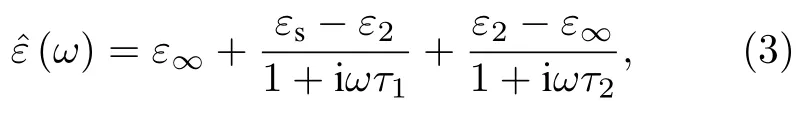
式中，ε∞為高頻極限相對介電常數，εs為靜態相對介電常數，ε2為中間值，τ1和τ2為兩次弛豫時間.慢弛豫時間τ1主要與氫鍵有關，它反映了從εs到ε2的變化.快速弛豫時間τ2與單個分子的重定向有關，它反映了從ε2到ε∞的變化.神經細胞內生理液擬合參數如表2 所列.

表2 等效神經細胞內生理液相對介電常數的二階德拜模型參數擬合結果Table 2. Second-order Debye model parameter fitting results of dielectric constant of the effective intracellular fluid in nerve cells.

從圖2(c)可以看出，實驗結果與0.3—2 THz的擬合結果符合較好.等效神經細胞內生理液體的相對介電常數隨頻率的增加而減小，在高頻THz范圍內接近光學相對介電常數ε∞.同時，隨著頻率的增加，相對介電常數的虛部與實部的比值會減小，說明太赫茲波在神經細胞中傳播時損耗更小.然后采用二階德拜模型模擬得到了等效神經細胞內生理液在0.3—50 THz 范圍內的介電響應特性，如圖3 所示.

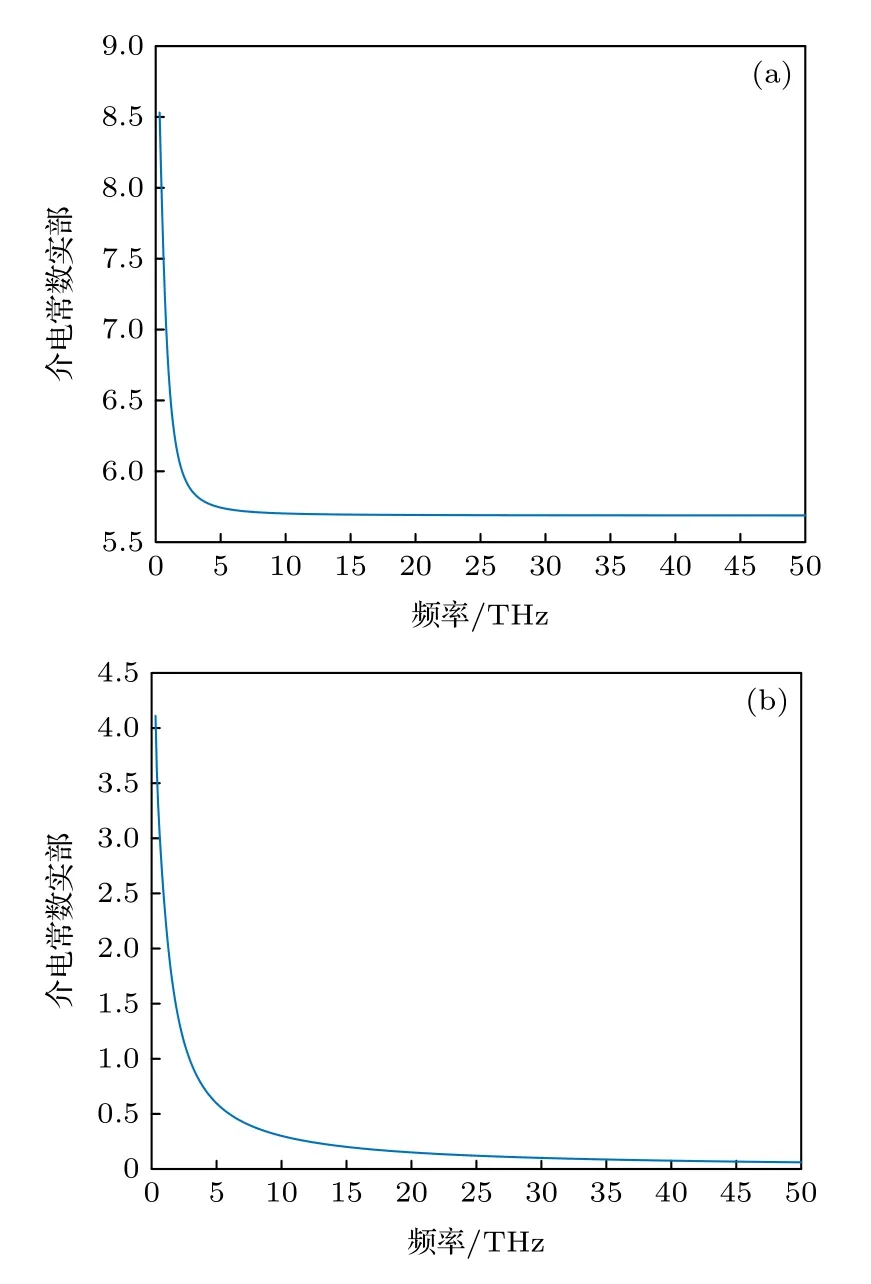
圖3 由二階德拜模型模擬等效細胞內生理液在0.3-50 THz 范圍內的相對介電常數 (a)實部;(b)虛部Fig.3.Dielectric constant of intracellular fluid in the range of 0.3-50 THz simulated by second-order Debye model:(a) Real part;(b) imaginary part.

2.3 太赫茲波在神經細胞中傳輸特性的計算方法

為了計算太赫茲波在神經細胞中的傳輸，采用FDTD 方法求解麥克斯韋方程組，該方法是在Yee單元[15]形成的離散時空網格上時域求解Maxwell方程的一種常用方法.在直角坐標系中，Maxwell方程可以轉化為6 個偏微分方程.

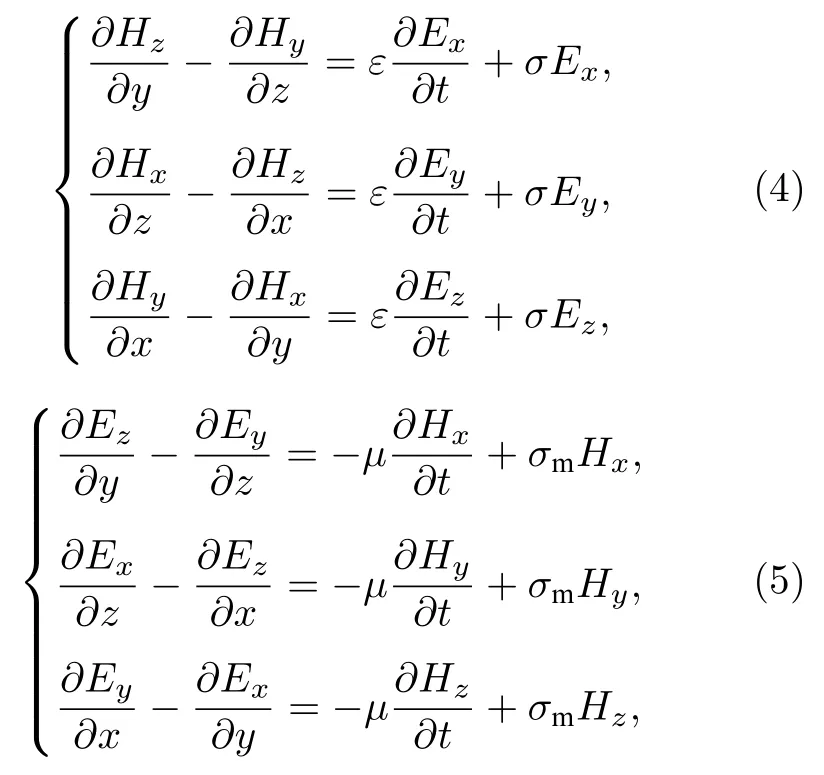
式中，H，E，ε，μ，σ分別為磁場強度、電場強度、介質介電常數、介質磁導率、電導率.

利用FDTD 方法計算太赫茲波在神經細胞中傳播特性的模型包括信號源、背景介質、神經細胞模型和完美匹配層(PML) 4 部分，如圖4(a)所示.模型中采用的太赫茲信號源為正弦形式的太赫茲波，其波形如圖4(b)所示.

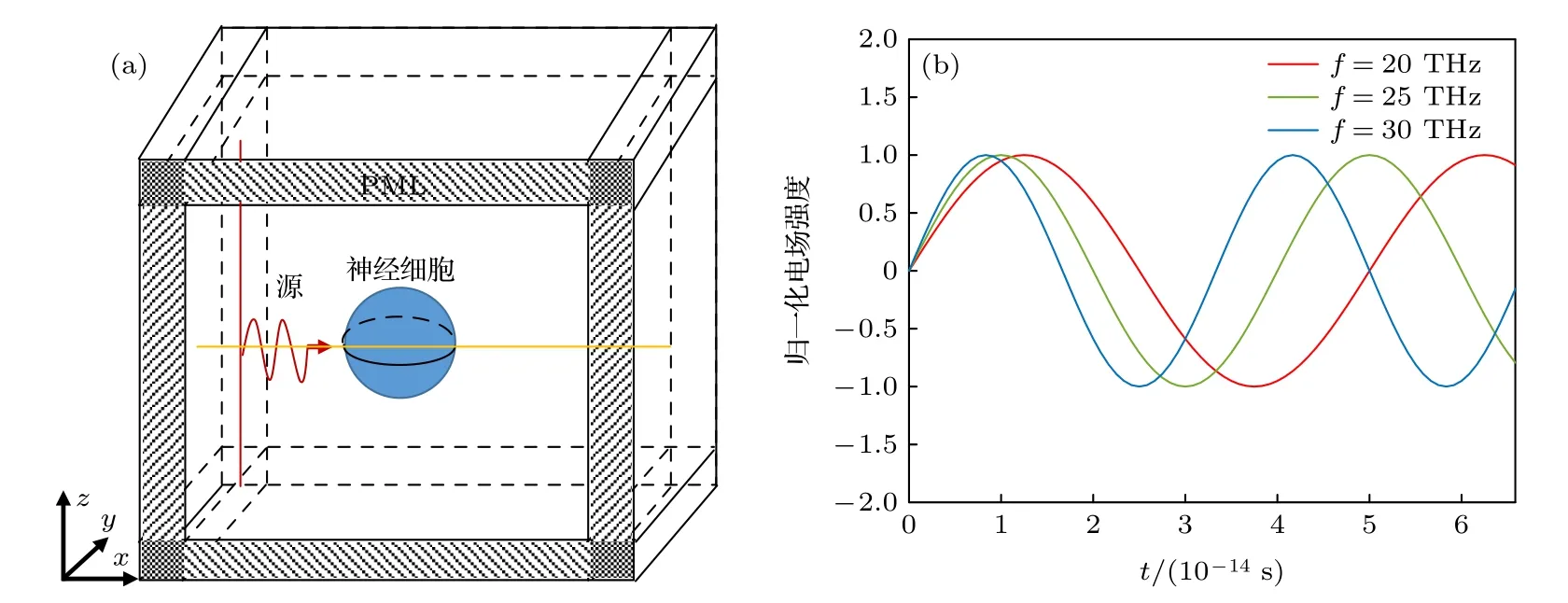
圖4 (a)太赫茲波在神經細胞中傳輸的三維FDTD 模型，太赫茲波由線源產生，以柱面波的形式向三維空間傳輸;(b)模擬過程中用到的3 種頻率(20，25，30 THz)的太赫茲輻射源波形Fig.4.(a) Three-dimensional FDTD model of THz wave transmission in the nerve cell.THz wave is generated by line sources and transmitted to three-dimensional space in the form of cylindrical wave.(b) THz source waveforms for the three frequencies (20，25，30 THz) used in the simulation.

神經細胞胞體由圖1 所示模型描述，細胞膜厚度為9 nm，細胞半徑為8 μm，細胞核半徑為1 μm.仿真中使用了單軸PML 用于吸收入射到邊界的太赫茲波以避免反射波的影響[16].電場和磁場的本構關系可以表示為

神經細胞可視為非磁性材料(μr1)，其介電常數可表示為εε0[εr+σ/(iω)] .由于神經細胞內生理液為極性液體，因此可以不考慮歐姆損耗(σ=0)，εr用二階德拜模型表示.考慮到細胞膜厚度(9 nm)遠小于太赫茲波長(30 THz 時為10 μm)，采用元胞計算法[17]將厚度為9 nm 的細胞膜等效到單個網格上進行模擬，這樣可以在保證計算準確的同時節省大量的計算時長.因此，(6)式和(7)式可以寫成如下形式:

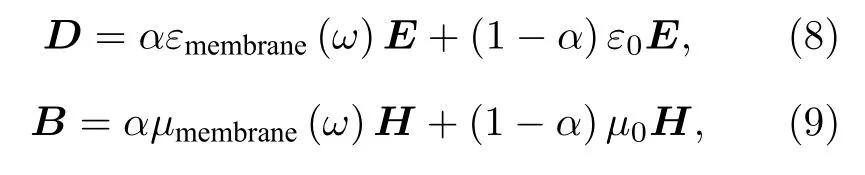
式中，α為單個網格中細胞膜的體積分數，εmembrane為細胞膜的相對介電常數，如(3)式所示，其中參數如表1 所列.由于仿真所用的單元模型是球形的，可以采用梯形網格處理方法來描述曲面邊界;同時考慮了元胞算法，邊界描述如圖5 所示.

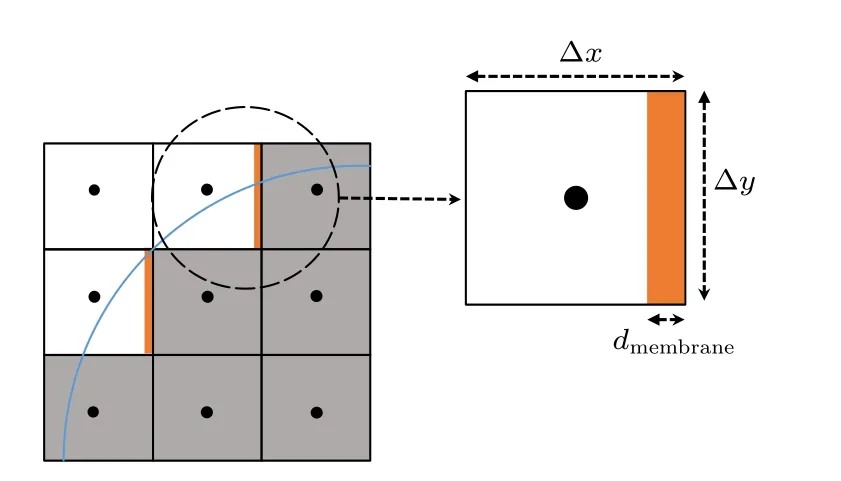
圖5 曲面邊界的梯形網格處理方法，橙色的區域是細胞膜Fig.5.Surface boundary trapezoidal mesh treatment，the orange area is the cell membrane.

細胞膜的體積分數α可表示為αdmembrane/Δx，其中，dmembrane為膜的厚度，Δx為單個網格的尺寸.灰色區域表示細胞所在的區域，白色區域表示細胞外部的背景媒質.當網格中心與細胞中心之間的距離小于或等于細胞半徑時，則被認為是細胞的內部.Yee 網格的空間步長與頻率有關，可以表示為dxdydzλ0/10，其中λ0為空氣中的波長，c為真空中的光速.時間步長可以表示為 dtdx/(2c) .

3 神經細胞的弱諧振特性

由于神經細胞(1—100 μm)的尺寸與太赫茲波長(3—100 μm)可比擬，太赫茲波與神經細胞可能會發生明顯的相互作用.在實驗測量結果的基礎上，利用FDTD 方法建立了一個物理模型，以研究太赫茲波在神經細胞中的傳輸特性、不同背景媒質與神經細胞的相對介電常數差異以及細胞尺寸和太赫茲波頻率對弱諧振效應的影響.另外，在球形神經細胞結構的基礎上，考慮到神經細胞結構上的特異性，建立了細胞體-軸突的神經細胞的物理模型，并進一步研究太赫茲在包含神經纖維的神經細胞中的傳輸特性.

3.1 不同背景媒質中的神經細胞弱諧振效應

采用FDTD 方法計算了圖4(a)所示的三維數學物理模型，同時，模型中電場的相對變化用增益系數G表示:

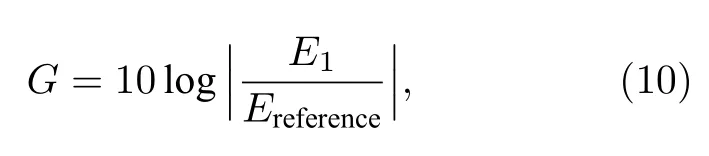
其中E1為包含神經細胞的模型中的電場幅值，Ereference 為不包括神經細胞的背景環境中的電場振幅.首先計算并分析了背景媒質的相對介電常數為1 時，由點源產生的頻率為30 THz 的太赫茲波在半徑為8 μm 的神經細胞中的傳輸特性，結果如圖6(a)所示.

由圖6(a)可看出:增益G的最大值(＞ 10 dB)位于神經細胞內部，太赫茲波與神經細胞相互作用可以在神經細胞內部產生較大的場增強效應;在神經細胞外邊界處，增益系數G出現了小于0 的情況，表明細胞內的太赫茲波只有極少的一部分透射出去而大部分的能量都被集中在了細胞內部，我們將這種效應稱為神經細胞的弱諧振效應.

為進一步分析細胞膜以及細胞核對弱諧振效應的影響，計算了只包含神經元細胞核以及細胞膜而無細胞內生理液的神經元細胞物理模型以及太赫茲波在純背景媒質中的傳輸模型，如圖6(b)中的紅色和黃色曲線所示.結果表明，對于細胞核等尺寸遠小于太赫茲波波長的細胞器來說，太赫茲波的繞射行為使得其對太赫茲波的傳輸影響可以忽略不計.

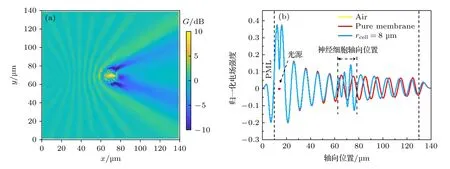
圖6 (a)頻率為30 THz 的太赫茲波在神經細胞中傳輸的增益G;(b)太赫茲波在空氣(黃色曲線)中、無神經細胞內生理液的模型(紅色曲線)以及含有神經細胞內生理液的細胞模型(藍色曲線)的一維場分布結果，其中黃色曲線與紅色曲線發生重疊Fig.6.(a) Gain of the THz wave transmission in nerve cells at a frequency of 30 THz;(b) one-dimensional field distribution results of the THz wave in air (yellow curve)，a model without intracellular fluid (red curve)，and a cell model with intracellular fluid (blue curve).The yellow curve overlaps with the red curve.

由于神經元分布在人腦組織的不同位置處發揮著不同的功能，而不同功能區的含水量以及組成成分不同，使得該部位的相對介電常數會有明顯的不同，因此，計算了不同相對介電常數的背景媒質中，神經細胞內部的太赫茲能量的變化.這里討論了背景媒質的相對介電常數分別為1，2，3，4，5和6 時的傳播情況，結果如圖7 所示.

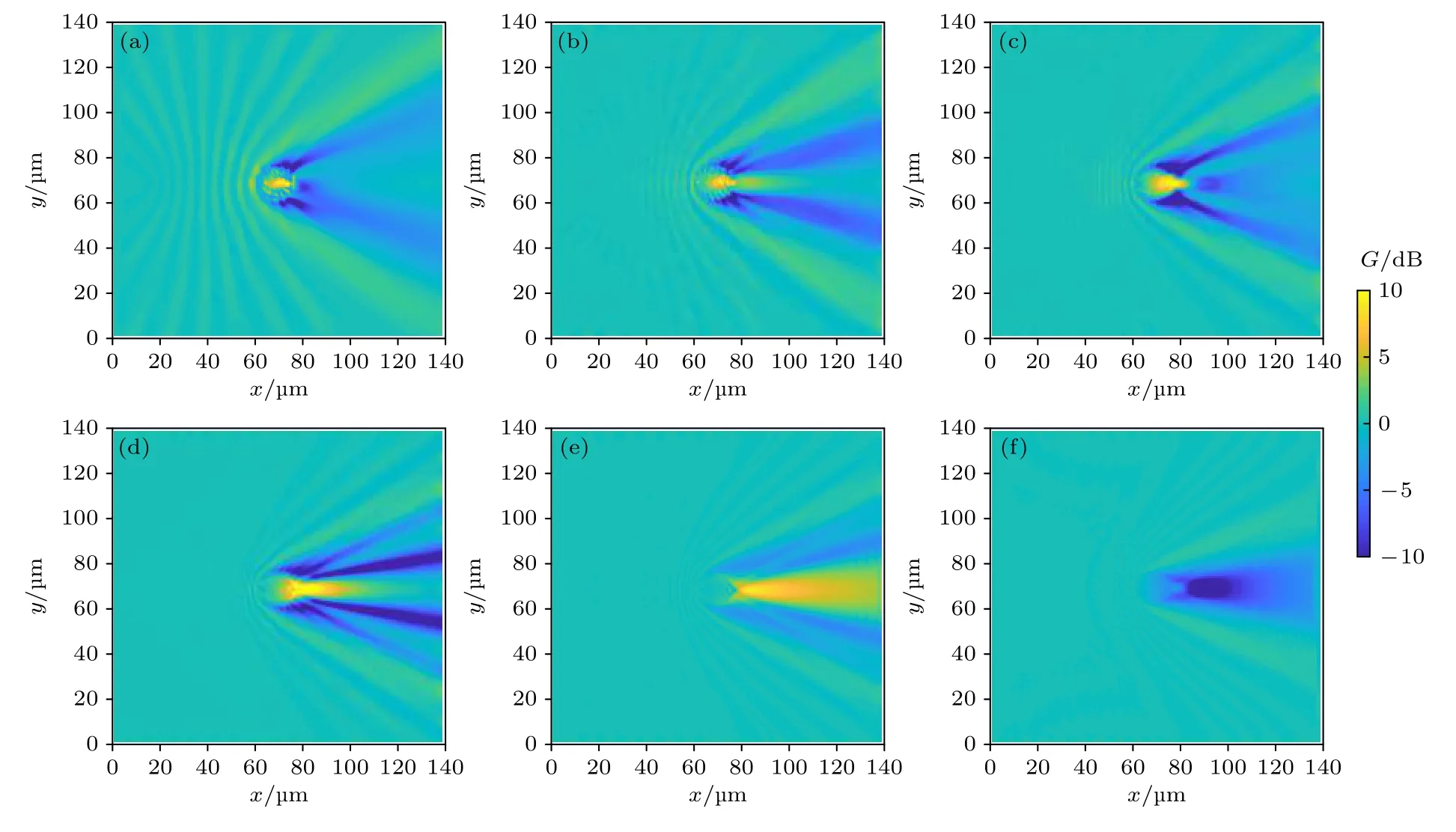
圖7 (a)—(f)背景媒質的相對介電常數分別為1，2，3，4，5 和6 時，神經細胞中的場增益G 結果，太赫茲波的頻率為30 THzFig.7.(a)-(f) Field gain results in the nerve cell when the dielectric constant of background medium is 1，2，3，4，5，6.The frequency is 30 THz.

頻率為30 THz 時，由二階德拜模型可以得到神經細胞的相對介電常數的實部為5.69，虛部為0.1，由圖7(a)—(d)的計算結果可以看出，隨著膜內外兩側相對介電常數差異的逐漸減小，弱諧振效應的峰值逐漸向后偏移，與此同時，神經細胞對太赫茲波的聚焦效應愈發明顯.當膜內外兩側相對介電常數的差值進一步減小時，由圖7(e)可以看出，球形的神經細胞可以看作是凸透鏡，可以使得細胞后側的電場進一步得到增強.當神經細胞的相對介電常數低于外部媒質時，弱諧振效應隨之消失.圖8給出了計算模型軸線上的場增益，其結果可以定量反映上述結論.

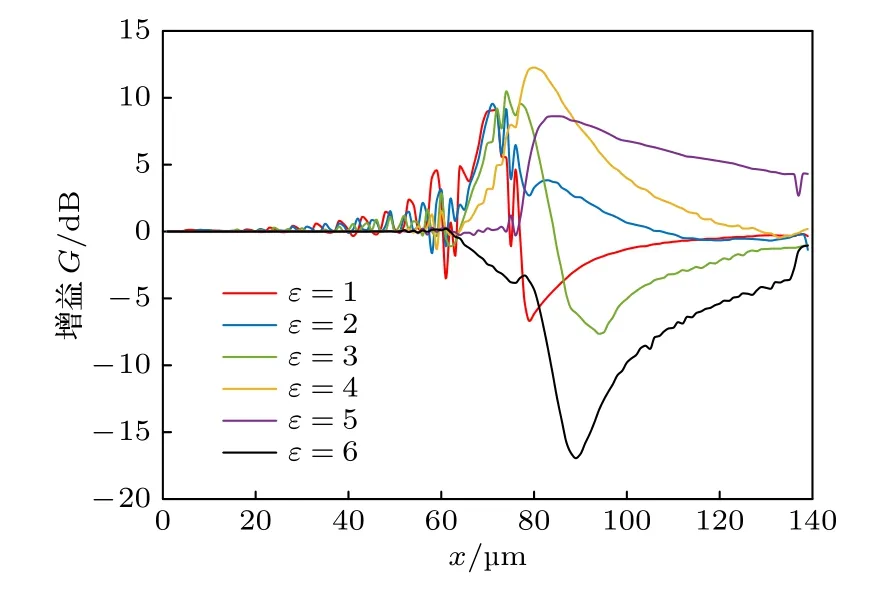
圖8 背景媒質的相對介電常數分別為1，2，3，4，5 和6時，頻率為30 THz 的太赫茲波在神經細胞中軸線上的增益G 曲線Fig.8.Gain curves on axis when dielectric constant of background medium is 1，2，3，4，5，6，and the frequency is 30 THz.

神經細胞不僅分布在腦組織等中樞神經系統中，在心肌、乳腺等組織中也發揮著重要的作用.有研究表明，乳腺癌轉移瘤的生長與周圍神經元的刺激有關[18]，文獻[19]給出了乳腺和癌變的乳腺組織的太赫茲頻段的二階德拜模型參數，如表3所列.

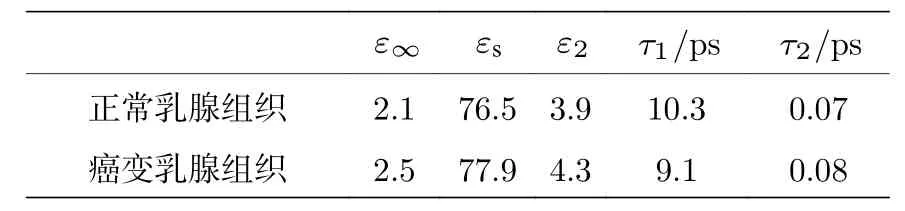
表3 正常的乳腺組織以及癌變的乳腺組織的二階德拜模型參數Table 3. Second-order Debye model parameters of normal and cancerous breast tissues.

用正常的乳腺組織和癌變的乳腺組織來代替原有的背景媒質，并分別計算了半徑為8 μm 的神經細胞在這兩個不同的媒質中的弱諧振效應的變化，計算結果如圖9 所示.

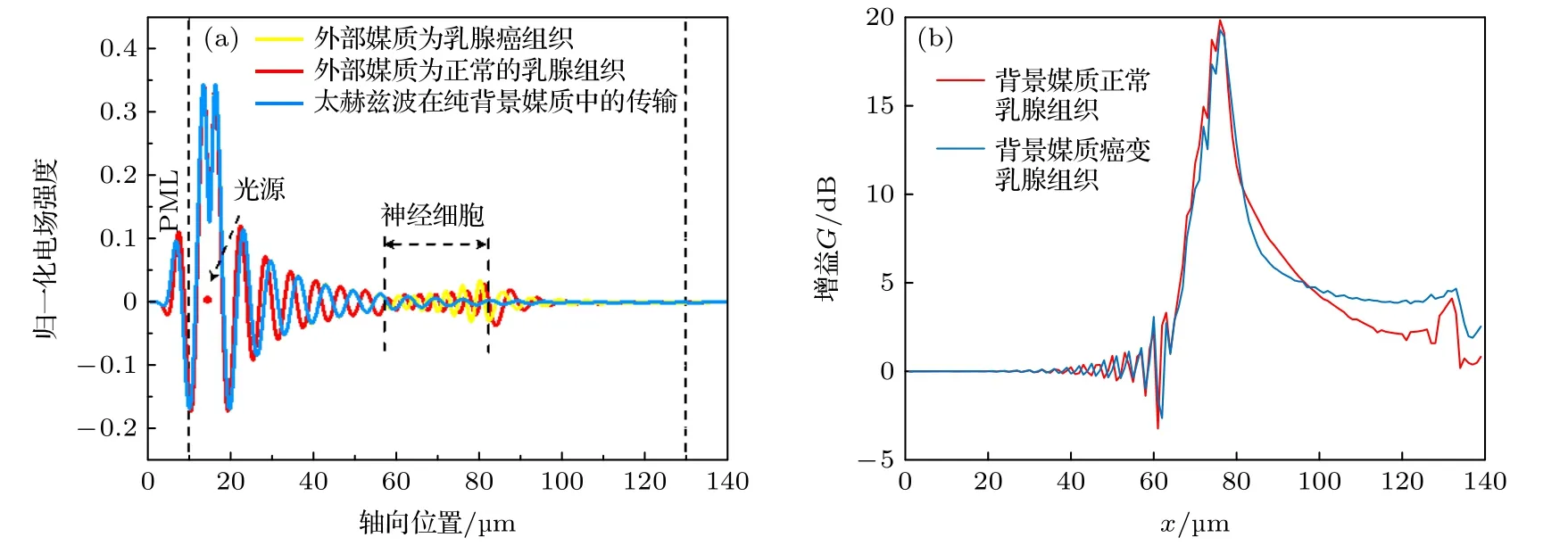
圖9 背景媒質為乳腺和癌變的乳腺組織時，頻率為30 THz 的太赫茲波在神經細胞中的(a)電場分布和(b)軸線上的增益Fig.9.(a) Electric field distribution and (b) gain of the 30 THz terahertz wave in nerve cells under the condition of breast and cancerous breast tissue in the background medium.

用二階德拜模型描述乳腺以及癌變的乳腺組織時，既可以反映媒質的相對介電常數，同時也可以很好地反映太赫茲波在生物組織中傳輸的衰減.計算結果表明，當無神經細胞時，由于乳腺組織對太赫茲波的吸收特性，電磁波快速衰減，當傳輸距離為100 μm 時，太赫茲波幾乎衰減為0;而當背景媒質為乳腺和癌變的乳腺組織時，由于神經細胞的相對介電常數高于兩種背景媒質，使得細胞內部的電場得到增強，進而傳輸距離也有所增加.同時，研究還表明，正常的乳腺組織中的神經細胞的增益系數G高于癌變的乳腺組織中神經細胞的增益系數G，說明正常乳腺組織中的神經細胞對太赫茲波的增強效應更為明顯.

3.2 神經細胞的弱諧振效應與細胞尺寸的關系

實際中，生物體的不同功能區以及不同分化階段的神經細胞的尺寸大小具有一定的差異，神經細胞體的尺寸小到幾微米，大到幾十微米，因此，需要研究不同尺寸的神經細胞(半徑分別為8，12.5和20 μm)中的弱諧振效應.對于太赫茲波頻率為30 THz，背景媒質的相對介電常數為1 的情況，計算結果如圖10 所示.

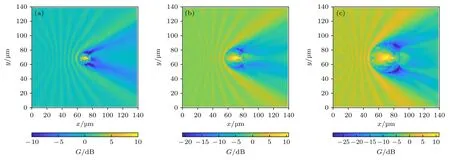
圖10 (a)—(c)神經細胞的半徑為8，12.5 和20 μm 時，太赫茲波在神經細胞中傳輸的增益GFig.10.(a)-(c) Gain of THz wave transmission in nerve cells with the radius of 8，12.5，20 μm.

研究表明，在給定頻率(30 THz)下，隨著細胞尺寸的增加，場增益也有一定程度的增強，一維軸線上的增益系數G如圖11 所示.

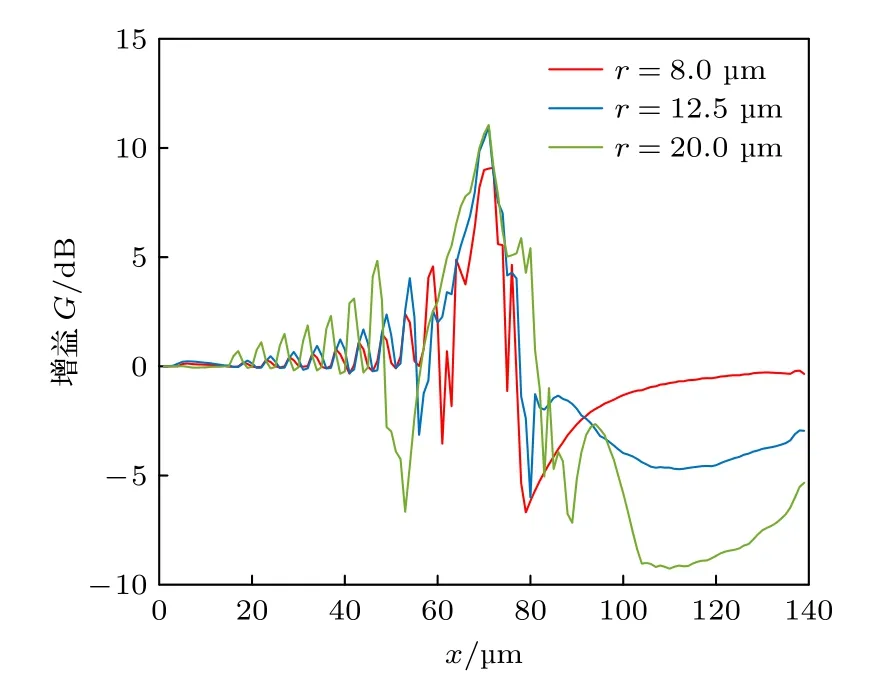
圖11 神經細胞的半徑為8，12.5 和20 μm 時，軸線上的場增益曲線Fig.11.Field gain curves along the axis of nerve cells with radius of 8，12.5 and 20 μm.

細胞內部電場的增強通常會導致細胞外側的電場的減弱.從圖11 可以看出，神經細胞的半徑為8，12.5 和20 μm 時，細胞內部電場的最大增益分別為11.1，11，9.1 dB，即隨著細胞尺寸的增大，增益系數G逐漸增強;細胞內部電場增強的同時，細胞兩側的反射波隨之增大，透射波也相應地減弱.由于水對太赫茲波的強吸收特性，當神經細胞的尺寸遠大于太赫茲波波長時，由膜一側透射進入到細胞內部的太赫茲波會被水吸收而衰減，導致難以與膜對側的反射波相互疊加產生駐波增強效應.進而弱諧振效應也會隨之消失.因此，無論對于尺寸遠小于太赫茲波長和尺寸遠大于太赫茲波長的神經細胞體來說，都難以產生弱諧振效應.

3.3 神經細胞的弱諧振效應與頻率的關系

由圖2(c)的實驗測量結果可以看出，隨著頻率的增加，相對介電常數的虛部與實部之比減小.計算當神經細胞尺寸一定(r=8 μm)時20，25，30 THz 這3 種不同頻率下的太赫茲波在神經細胞模型中的傳播特性，結果如圖12 所示.

隨著太赫茲波頻率的增加，細胞內部的場增強效應愈發明顯，圖13 給出了圖12 軸線上的電場增益系數G，當頻率為20，25，30 THz 時，細胞內部的最大增益分別為12.2，10.3 和8.3 dB.結果表明，當細胞尺寸一定時，隨著頻率的升高，細胞內的增益明顯提升，細胞對太赫茲波的束縛效果也更加明顯.當場主要集中在細胞內部時，透射波的能量也相應減弱.

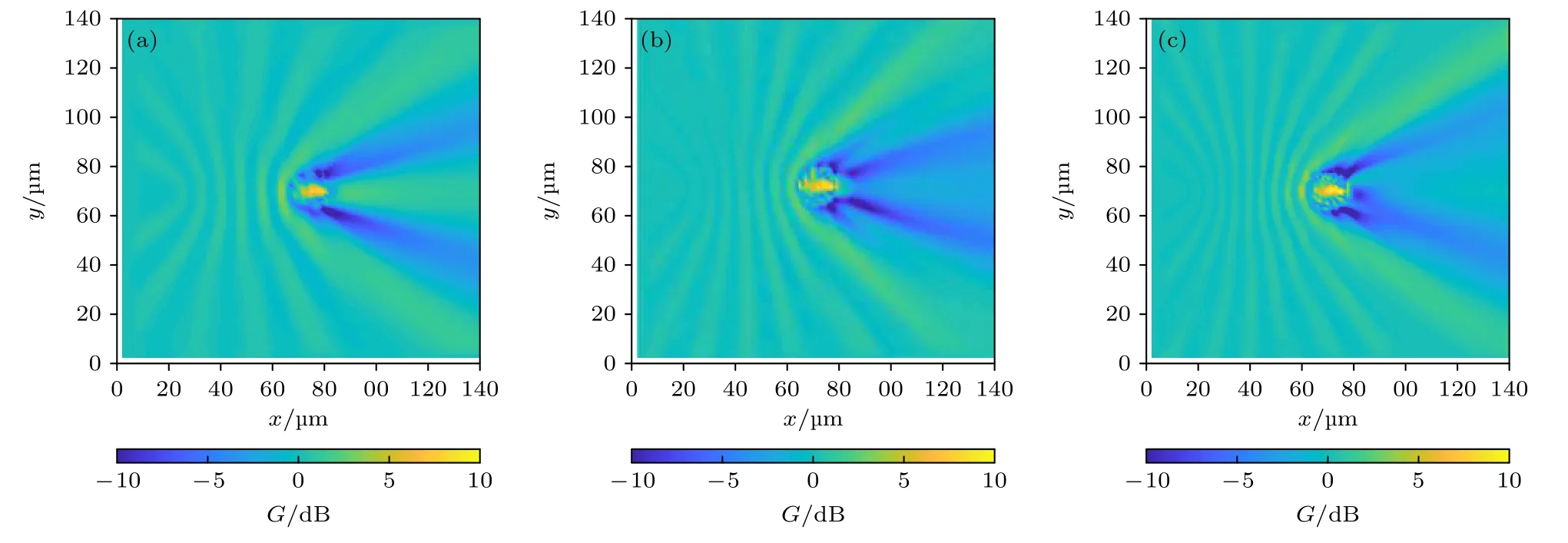
圖12 3 種不同頻率的太赫茲波通過神經元細胞傳播的特性 (a) 20 THz;(b) 25 THz;(c) 30 THzFig.12.Characteristic of three THz waves of different frequencies transmitting through the neuron cell:(a) 20 THz;(b) 25 THz;(c) 30 THz.

圖13 神經細胞弱諧振效應與太赫茲波頻率的關系，細胞中心位于70 μm 處Fig.13.Relation between weak resonance effect and THz frequency of nerve cells，cell center at 70 μm.

介質諧振器能使電磁波在介質中反射，形成諧振結構.高相對介電常數的介質確保大部分的場在諧振腔中，不受輻射或泄漏的影響.神經細胞的弱諧振效應也可以通過固有品質因數Q值得到解釋:

式中，tanδ與媒質的損耗有關，由于神經細胞內部的生理液主要是以水為主要成分的極性液體，因此，媒質的損耗主要為極化損耗，可以表示為tanδε′′/ε′.由圖3 可以看出，隨著頻率的升高，細胞的極化損耗逐漸降低，當頻率高于30 THz 時，神經細胞的Q值大于50，說明神經細胞能夠將電磁能量集中到細胞內部.當頻率分別為20，25，30 THz 時，細胞體的Q值分別為37.8，47.2，56.6.由于細胞的Q值隨著頻率的增加而增加，細胞將更多的高頻太赫茲場的能量集中在細胞內，產生諧振特性.

3.4 太赫茲波在神經細胞-軸突中的傳輸特性

為研究神經元胞體的弱諧振效應對太赫茲波在神經纖維中傳輸的影響，在圖1 所示的神經元胞體模型后增加了一段長為50 μm、半徑為5 μm 的神經軸突，其中包括2 μm 厚的髓鞘結構.隨后計算了頻率為30 THz 時的場增益，結果如圖14 所示，其中髓鞘的相對介電常數為9，軸突的相對介電常數為4，參數可以由文獻[2]得到.這里討論背景媒質的相對介電常數為2 和4 的情況，細胞體的相對介電常數由二階德拜模型來描述.

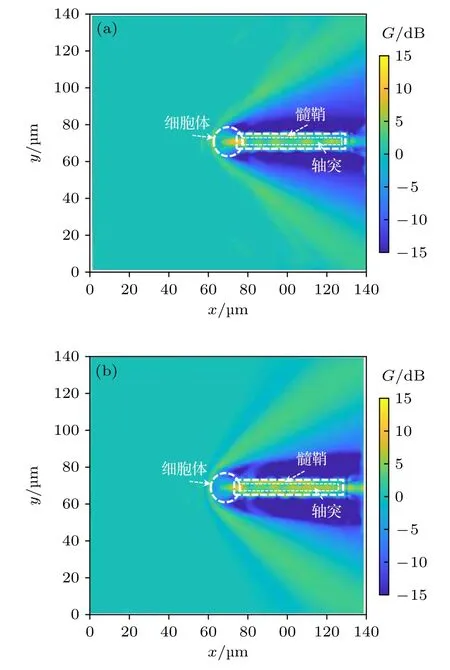
圖14 背景媒質的相對介電常數為(a) 2，(b) 4 時，神經細胞-軸突模型中的場增益G 結果Fig.14.Field gain results in the neuron-axon model，when the relative permittivity of background medium is (a) 2 and(b) 4.

由計算結果可以看出，神經細胞的弱諧振效應使得太赫茲波在細胞內得到增強并沿著神經纖維繼續傳輸，弱諧振效應隨著膜兩側介電常數的差值減小而逐漸增強.同時，太赫茲波的能量被主要局限在細胞體以及髓鞘中，說明了太赫茲波在神經細胞中傳輸的可能性.

4 結論

本文建立了包含細胞膜、細胞內生理液以及細胞核的三層結構的神經細胞胞體的物理模型來研究太赫茲波在神經細胞中的傳輸特性.由于單細胞的相對介電常數難以精確測量，利用THz-TDS 系統測量了等效的神經細胞內部生理液的相對介電常數，并用二階德拜模型對測量結果進行擬合，擬合結果與實驗結果保持一致.利用FDTD 方法從理論上研究了太赫茲波在神經細胞中的傳輸特性，結果表明，細胞器以及細胞核等尺寸遠小于波長的小目標物體對太赫茲波傳輸過程產生的影響可以忽略不計.由于神經細胞遍布周身，包括腦組織在內不同組織的相對介電常數都有明顯的差異，研究了不同背景媒質中的神經細胞對太赫茲波傳輸的影響.結果發現，隨著膜內外兩側相對介電常數差異的逐漸減小，弱諧振效應的峰值逐漸向后偏移;當細胞與背景媒質的相對介電常數相差無幾，且細胞的相對介電常數高于背景媒質時，神經細胞對太赫茲波會產生聚焦效應.通過研究不同頻率的太赫茲波以及不同尺寸的神經細胞發現，頻率一定時，隨著細胞尺寸的增加，弱諧振效應有一定程度的增強;尺寸一定時，隨著太赫茲波頻率的升高，弱諧振效應也有一定程度的增強.在神經元球形結構的基礎上，考慮了神經細胞結構上的特異性，建立了細胞體-軸突物理模型，通過分析細胞體-軸突中的場增益，發現神經細胞的弱諧振效應也會進一步增強太赫茲信號在神經纖維中的傳輸.

本文通過理論分析提出了神經細胞的弱諧振效應，為研究太赫茲波與神經細胞的相互作用提供了一種策略.由于人體內不同組織中的細胞對太赫茲波傳輸的增強效應不同，使得這一結論有助于解釋人體內太赫茲信息傳輸的途徑.