讓課堂成為生命的息壤

林林

摘要：伴隨著初中數學新課標的實施，一線教師開啟了如火如荼的改革策略，結合這些策略，雖然看起來非常人性化，但我認為教師最好的教學模式是將課堂真正還給學生，初中數學課堂要教會學生開展深度學習。一直以來，后進生學習的提升是我們每一個教師工作中的重點，本文從五個方面闡述了初中數學課堂如何引導后進生參與深度學習：趣味導入，引導學生產生興趣;小組合作，引導學生分享交流;積極質疑，引導學生獨立思考;拓展延伸，引導學生自主學習;迎難而上，引導學生知難而進。

關鍵詞：初中數學;核心素養;引導;讓學習真正發生;后進生引導

中圖分類號：G4 文獻標識碼：A

這一年來，核心素養這個詞匯成了全國范圍內的熱門詞匯，核心素養的培育目標下，作為教師的我們就要不斷反思我們的課堂，是否給予學生帶來了真正的課堂？是否讓學生在課堂內真正發生？教師每一天面對的都是一各個鮮活的個體，學校的課程設置都是從學生的生命教育的角度出發的，哪怕是數學這樣的學科，通過引導學生對宏觀世界和微觀世界的認知，引導學生最終實現認識世界、改變世界的這個過程。一直以來，初中數學課堂教學由于受到傳統教學模式的影響，學生的學習習慣和學習自主性方面都不太理想。

一、趣味導入，引導后進生產生興趣

后進生之所以學業成績不理想，主要還是與其學習興趣有關系。兩千多年前的孔子曾經說過：“知之者不如好之者，好之者不如樂之者。”結合初中學生的身心發展特點和自身素養，學生學習興趣的匱乏，很容易引起厭學等狀況，學生的學習積極性、學習自主性等方面也會受到一定的影響。所以為了引導學生深度學習，我從課堂導入入手，結合趣味導入的方式，引導學生對于所學的知識點產生濃郁的興趣。

以平行四邊形的教學為例，教學中我給出以下問題：1、怎樣判斷一個四邊形是平行四邊形？2、怎樣判斷一個四邊形是菱形？3、怎樣判斷一個四邊形是矩形？根據上面的回答，構建關系圖：（請在箭頭線上填寫判定方法）

緊接著，我給圖片：請同學們根據下圖，如何判定一個正方形呢？（結合幾何畫板，進行動畫演示）

學生形成結論：（1）定義法：即平行四邊形有一個角是直角，并且有一組鄰邊相等，那么這個平行四邊形是正方形;（2）先判定一個四邊形是矩形，再判定這個矩形是菱形，那么這個四邊形是正方形;（3）先判定四邊形是菱形，再判定這個菱形是矩形，那么這個四邊形是正方形。通過這樣的課堂引入，引導學生對于幾何語言的嚴謹、完整、準確有一個整體上的精確理解和把握。

二、小組合作，引導后進生分享交流

后進生普遍來說，對于合作學習的積極性不是很高。對于如今初中的這一代學生，他們基本上都是家中的獨生子女，從小生活在養尊處優的環境之中，學生的合作意識、分享意識都比較薄弱。近年來，合作學習成為了一個教學中的熱點話題，但是基于小組合作學習的開展，不少學生在分享交流的過程中出現一些障礙，比如學生不善于合作和交流，對于與他人合作產生抵觸情緒等。結合核心素養的教育理念，我結合小組合作的教學方法，引導學生參與合作，通過合作實現博采眾長的目的，學生之間可以相互吸收對方身上具備的優點，在合作學習的模式下，學生可以更高的提升自身的學習效率。

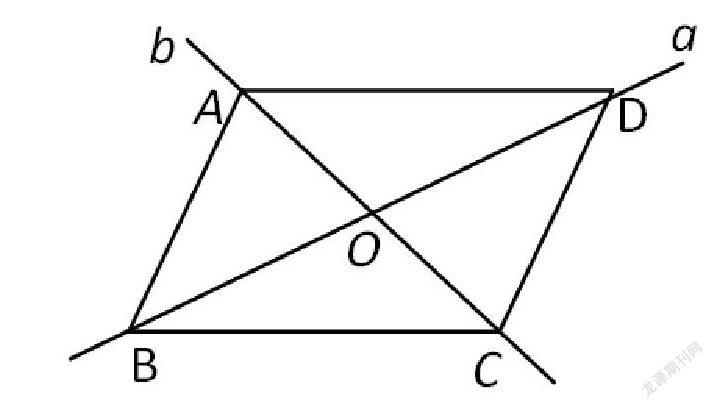
操作要求：1.畫2條相交直線a，b，設交點為O

思考：說明所畫四邊形是平行四邊形.（給學生合作交流時一定的思考時間，鼓勵用多種方法來解決）

【設計意圖】在開展前先讓學生探討并在草稿紙上思考，有了這一基礎，學生在認知上會有這樣的意識：用已學過的平行四邊形的判定來解決新的問題.設計中鼓勵學生用多種方法來解決有助于學生的發散性思維.同時，學生可能沒有想到利用中心對稱來解決問題，可根據學生的不同回答引導其用本章節的知識：從中心對稱的角度來考慮問題.

教師總結：如圖：OA=OC，OB=OD.△BOC可以看成由△DOA繞點O旋轉180 得到.

所以由中心對稱的性質，得∠OBC =∠ODA，所以AD‖BC

同理可得：AB∥DC

所以四邊形ABCD是平行四邊形。

師生共同總結得出得出結論：兩條對角線互相平分的四邊形是平行四邊形.

請學生嘗試用數學語言來表述上一結論。

總而言之，初中數學教學中如何引導后進生開展深度學習，對于培養學生良好的學習習慣、培育學生自主學習能力，都有著積極的價值和意義。與此同時，我深深體會到，作為一名初中數學教師，要在今后的教學中不斷總結教學的經驗，真正實踐將課堂還給學生，讓學生成為課堂的主體，才能真正構建人性化的有效科學課堂。