爆炸反應裝甲作用場下近炸引信作用距離計算模型

唐輝，焦志剛，趙東志，趙麗俊，，朱小平

(1.沈陽理工大學 裝備工程學院，遼寧 沈陽 110159；2.北方華安工業集團有限公司，黑龍江 齊齊哈爾 161000)

0 引言

現今，主戰坦克大多數都披掛了爆炸反應裝甲[1-2]。如何有效地規避爆炸反應裝甲的爆炸作用場并有效毀傷坦克裝甲目標成為一個研究熱點。為此，世界各國研究人員都在引信和戰斗部配合方式上進行創新。

在以身管武器為發射平臺的反坦克彈藥中，破甲彈需要解決近炸引信與串聯式聚能裝藥戰斗部之間的引戰配合問題。樣機設計初期，沒有可供參考的射表，因此，推算一級近炸引信作用距離的理論參考值尤為關鍵[3]。為了解決這一問題，本文運用低伸彈道的西亞切近似分析解法解算彈道[4-5]，得到彈道各點的彈丸速度v，建立計算模型，推出極限交會距離L，進而推導出引信作用距離S與彈速v的關系，求出在彈道各點的一級引信最佳作用距離。計算模型解出的各組S-v解析值以數據表形式被寫入引信發火控制系統算法，近炸引信可根據裝甲目標特性的差異調用不同彈目交會條件下的S-v數據表，以實現其作用距離的動態自適應控制，提高彈藥的毀傷效率。

1 低伸彈道的西亞切近似解法推導

經典外彈道學給出了自然坐標系下以飛行時間t為自變量、以速度v運動的彈丸質心運動方程組，對于射角φ0≤5°的低伸彈道，忽略重力加速度的影響，并令ds=vdt，s為彈道孤長，則有彈丸質心運動方程組簡化如下：

(1)

(2)

(3)

(4)

(5)

式中：c為彈道系數；Hτ(y)為空氣密度函數，τ為虛溫；G(vτ)為阻力函數，vτ為地面標準虛溫條件下的速度；y為彈道高；φ為彈道傾角；x為水平彈道長；τs為虛溫地面標準值。

D(vτ)-D(vs)=cH(y0)x，

(6)

2 計算模型建立

典型坦克炮用串聯式戰斗部破甲彈為長鼻形兩級破甲戰斗部串聯結構，根據其破甲作用機理，彈丸需要避開爆炸反應裝甲的反擊彈射流[6-9]。

固定反應裝甲位置，反擊彈射流軌跡相對安裝位置也固定。目標各參數不變時，破甲彈瞄準反應裝甲有效區的最上沿時具有極限作用距離，即此時彈丸頭部與目標之間取得極限交會距離。

2.1 極限交會距離計算

爆炸反應裝甲內置鈍感炸藥夾層和多發不同斜置角的聚能裝藥反擊彈，用以形成反擊彈射流帶，擴大對來襲彈藥的毀傷區域[10-12]。其基本結構如圖1所示。反應裝甲斜置傾角θ、鈍感炸藥夾層與反應裝甲背板夾角γ、反擊彈支座與鈍感炸藥夾層夾角β及反擊彈射流帶右邊界出射角α之間的關系為

圖1 爆炸反應裝甲結構示意圖

α=90°-θ-γ-β.

(7)

對于彈徑為D的二級串聯式戰斗部破甲彈，二級戰斗部被反擊彈擊中損毀即可認定為彈丸喪失毀傷效能。根據推算，一級戰斗部擊中反應裝甲有效區的最上沿時為極限情況，圖2所示為主射流擊中點即為反應裝甲有效區的最上沿。

圖2 彈目交會臨界點示意圖

圖2中，D1為一級戰斗部射流穿孔與反擊彈射流穿孔之間的高度差，L為極限交會距離(即極限交會處彈丸肩部與反應裝甲的距離)，L1為面板穿孔與彈丸肩部水平距離，H1為反應裝甲面板兩端邊界點之間高度差，H2為反擊彈射流穿孔與面板右端邊界點之間高度差，H3為一級戰斗部射流穿孔與面板左端邊界點之間高度差。

此時，彈軸線與反擊彈在反應裝甲面板上的穿孔位置垂直高度為

D1=H1-H2-H3.

(8)

根據圖2所示破甲彈與反應裝甲反擊彈射流交會的臨界位置示意圖，可得

L1=(D/2+D1)/tanα，

(9)

L=L1+D1/tanθ.

(10)

需要說明的是，對于不同的坦克裝甲目標，其首上裝甲的傾角也不同。根據(10)式可知L=L(L1，D1，θ)，θ為變量之一，爆炸反應裝甲設置不同的傾角時，可得到與之對應的新的極限交會距離L，從而使得本文建立的計算模型具備普遍適用性。

2.2 引信作用距離計算

一級近炸引信采用定距發火起爆一級戰斗部，不同彈道長對應不同的引信作用距離，但對于某一時刻，炮目距離是一定的，則由(6)式可算出x處彈丸速度v，以用于建立計算模型中各參數之間的關系式。

一級戰斗部作用從引信探測裝置提供起爆信號開始，一級戰斗部形成射流、一級戰斗部射流飛行至目標、射流擊爆反應裝甲、反應裝甲反擊彈射流形成，此過程彈目運動模型如圖3所示。圖3中：t1為一級戰斗部射流形成時間；t2為一級戰斗部射流到達反應裝甲時間；t3為一級戰斗部射流到達反應裝甲時到反應裝甲被擊爆時間(由實驗測得)；t4為反擊彈射流形成時間；t5為反擊彈射流到達彈丸肩部時間。

圖3 彈目運動模型

根據以上引戰作用過程，一級近炸引信作用距離公式推導如下：

S=L-L2+v(t1+t2+t3+t4+t5)，

(11)

(12)

v2=v+vs，

(13)

(14)

式中：L2為彈丸頭部至彈丸肩部距離；X為反擊彈射流飛至彈丸肩部距離；vs為一級戰斗部靜態射流速度，由實驗測得；vd為一級戰斗部動態射流速度；vh反應裝甲反擊彈頭部射流速度，由實驗測得)

坦克炮射破甲彈的有利炸高一般為3～5倍裝藥直徑，其值小于極限交會距離L，為保證侵徹威力，二級主戰斗部必須采取延時起爆方式運動到小于臨界值L的范圍內侵徹主裝甲。因此，必須保證二級主戰斗部飛至L處時反擊彈射流已經越過彈丸肩部。圖2中，當彈目處于極限交會狀態時，反擊彈射流帶右邊界的射流剛好越過彈丸肩部。隨著彈丸繼續行進，由于反擊彈射流速度遠大于彈丸速度，處于射流帶左側的射流也已全部越過彈肩。因此，反擊彈射流不與彈丸交會的臨界條件為

X·cosα>L1.

(15)

此處反擊彈在反應裝甲盒內的行進距離極小，可忽略。將(12)式～(15)式代入(11)式，即可推出以彈丸速度v為自變量、一級引信作用距離S為因變量的關系式F(v，S)=0.其中S與v并非呈一次線性關系，而是正相關關系。

坦克炮破甲彈的常用作戰距離一般在1 000 m以內，通過以上理論計算方法，以某型破甲彈(1 000 m處著速為700 m/s)為例，推導出極限交會距離分別為1.27 m和1 000 m內一級近炸引信的理論作用距離與彈丸速度的對應關系如圖4所示。

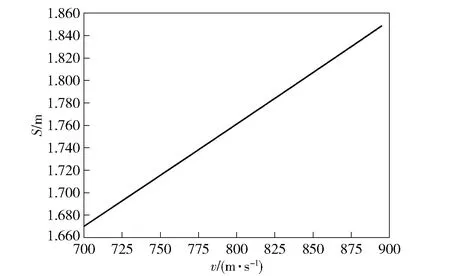
圖4 引信作用距離—彈速圖

從圖4中可以看出，在保證極限交會距離的前提下(即反擊彈射流剛好越過彈丸肩部)，S與v呈正相關關系。當彈丸飛至距炮口x1處時，v1=895 m/s，S1=1.85 m，即在一級近炸引信發火控制系統寫入算法時，應保證彈速為895 m/s，一級引信在距反應裝甲1.85 m處開始發火。彈丸在全彈道作變加速度的減速運動，當飛至距炮口x2處時v2=700 m/s，S2=1.67 m，即當引信在彈速為700 m/s時察覺到目標，應保證引信在距反應裝甲1.67 m處開始發火。彈速越高的作用點，一級近炸引信的作用距離應當越遠。

2.3 射流失穩計算

除考慮極限交會條件下彈目運動的幾何關系外，反擊彈射流的拉伸狀態也需加以分析。聚能射流具有很高的頭部速度和較低的尾部速度，大炸高下射流長度不斷延伸，當射流失穩斷裂，射流粒子會發生偏離、飛散和翻轉，其侵徹能力會顯著下降[13-15]。

射流斷裂時間tc計算公式為

(16)

式中：lc為射流頸縮長度；li為射流初始長度；vt為射流尾部速度。

當模型處于彈目交會臨界點時，t5>tc，反擊彈射流已經發生斷裂處于失穩狀態，必然會出現射流濺射等情況，其侵徹能力大幅減弱，此時可認為對有一定厚度彈體保護的主戰斗部聚能裝藥基本無威脅。

3 試驗驗證

為驗證L臨界值的合理性，對爆炸反應裝甲進行目標特性分析，并根據一級戰斗部作用距離理論計算值，布置爆炸反應裝甲威力場靜態驗證試驗，共設置6組不同的彈丸與反應裝甲距離L，對不同距離上的反應場威力進行驗證。試驗布置及試驗效果如圖5、圖6所示。

圖5 試驗布置情況

圖6 驗證試驗效果圖

采集數據并對數據進行分析，得到詳細試驗數據結果如表1所示。

從表1中可以看出：當設置不同的彈丸與反應裝甲距離L，隨著L增大，威力場逐漸減弱，反擊彈對目標的毀傷效果降低；當L增大到1.2 m時，反擊彈射流穿深僅為3 mm，且濺射范圍大。

表1 爆炸反應裝甲威力場試驗結果

4 結論

為提高爆炸反應裝甲作用場下的引戰配合效能，本文針對串聯戰斗部破甲彈的近炸引信作用距離問題，利用低伸彈道的西亞切近似解法解算彈道，進而建立了近炸引信作用距離的理論計算模型，并通過試驗對計算模型的合理性進行了驗證。得到如下主要結論：

1)經爆炸反應裝甲威力場靜態試驗驗證：當L≤0.8 m時，反擊彈威力場集中，其對來襲目標毀傷效果極強；當0.8 m1.2 m時，反擊彈射流穿深應小于3 mm，由于破甲彈丸本身彈壁有一定厚度，所以此時可認為反擊彈的威脅基本消除，可認定L=1.2 m為安全臨界值。

2)每個S值都是基于L值推導而來，依據理論計算模型導出的L=1.27 m，與驗證試驗得到的安全臨界值1.2 m基本吻合，因此，在此基礎上，依據本文方法建立的計算模型推導出的1 000 m內一級引信作用距離S的理論計算值合理可行。采用低伸彈道發射的近炸引信彈藥引戰配合參數理論值的設計可參考此模型。

參考文獻(References)

[1] 曹賀全，張廣明，孫素杰，等.裝甲車輛防護技術研究現狀與發展[J].兵工學報，2012，33(12):1549-1554.

CAO H Q，ZHANG G M，SUN S J，et al.Status and development of protection technology of armored vehicles[J].Acta Armamentarii，2012，33(12):1549-1554.(in Chinese)

[2] 房凌暉，鄭翔玉，馬麗，等.坦克裝甲車輛裝甲防護發展研究[J].四川兵工學報，2014，35(2):23-26.

FANG L H，ZHENG X Y，MA L，et al.Armor protection development of tank & armored vehicle[J].Journal of Sichuan Ordnance，2014,35(2):23-26.(in Chinese)

[3] 田博，施坤林，鄒金龍，等.近炸引信炸點對彈藥毀傷評估的影響[J].探測與控制學報，2020，42(6):1-7，12.

TIAN B，SHI K L，ZOU J L，et al.Fuze explosion point effect on ammunition damage assessment[J].Journal of Detection & Control，2020，42(6):1-7，12.(in Chinese)

[4] 劉鵬，王雨時，聞泉，等.超音速彈丸低伸彈道的近似解析解[J].探測與控制學報，2016，38(4):42-46，51.

LIU P，WANG Y S，WEN Q，et al.Approximate analytical expression of supersonic projectile low trajectory[J].Journal of Detection & Control，2016，38(4):42-46，51.(in Chinese)

[5] 王連敏.低速低伸彈道解法[J].兵工學報，1981，2(1):11-18.

WANG L M.A solution of the low-speed and flat trajectory[J].Acta Armamentarii，1981，2(1):11-18.(in Chinese)

[6] 黃鶴，陳建申，徐鵬，等.破甲反擊彈抗串聯戰斗部的可行性[J].兵工自動化，2019，38(8):55-57.

HUANG H，CHEN J S，XU P，et al.Feasibility of anti-series warhead of HEAT counter-attack projectile[J].Ordnance Industry Automation，2019，38(8):55-57.(in Chinese)

[7] 郎明君，徐學華.多級串聯聚能裝藥隔爆時間的計算與測試[J].南京理工大學學報，2002，26(6):625-627，631.

LANG M J，XU X H.Calculation and test on flame-proof time of multistage-series shaped charge[J].Journal of Nanjing University of Science and Technology，2002，26(6):625-627，631.(in Chinese)

[8] 史志鑫.串聯毀傷元對斜置反應裝甲目標的侵徹性能研究[D].太原：中北大學，2020.

SHI Z X.Research on the penetration performance of tandem damage element to oblique reaction armor target[D].Taiyuan：North University of China，2020.(in Chinese)

[9] 萬清華.多三明治結構反應裝甲干擾射流作用研究[D].太原：中北大學，2019.

WAN Q H.Interference effect of reactive armor with multi-sandwich on shaped charge jet[D].Taiyuan：North University of China，2019.(in Chinese)

[10] 萬清華，李如江，楊玥，等.多三明治結構反應裝甲干擾射流的數值模擬[J].高壓物理學報，2018，32(6):123-130.

WAN Q H，LI R J，YANG Y，et al.Numerical simulation of interference effect of multi sandwich structure reaction armor to jet[J].Chinese Journal of High Pressure Physics，2018，32(6):123-130.(in Chinese)

[11] 張樂.某結構反應裝甲對射流干擾的機理研究[D].南京：南京理工大學，2016.

ZHANG L.Research on the interferences principle of the ERA to jets[D].Nanjing：Nanjing University of Science and Technology，2016.(in Chinese)

[12] 熊良平，黃道業，王鳳英.新型反應裝甲結構對長桿彈小法線角侵徹的干擾分析和防護效能[J].爆炸與沖擊，2013，33(1):108-112.

XIONG L P，HUANG D Y，WANG F Y.Protection effectiveness of a new explosive reactive armor against penetration of long-rod projectiles with small yaw angles[J].Explosion and Shock Waves，2013，33(1):108-112.(in Chinese)

[13] 石藝娜，秦承森.金屬射流失穩斷裂的理論分析[J].力學學報，2009，41(3):361-369.

SHI Y N，QIN C S.Instability and breakup of stretching metallic jets[J].Chinese Journal of Theoretical and Applied Mechanics，2009，41(3):361-369.(in Chinese)

[14] 黃正祥.聚能裝藥理論與實踐[M].北京:北京理工大學出版社，2014.

HUANG Z X.Theory and practice of shaped charge[M].Beijing:Beijing Institute of Technology Press，2014.(in Chinese)

[15] 王樹山.終點效應學[M].北京:科學出版社，2019.

WANG S S.Terminal effects[M].Beijing:Science Press，2019.(in Chinese)