分形煤層氣藏有限導流多翼壓裂直井試井模型

鄒文龍， 余 輝， 郭 佳， 石美雪

( 1. 深圳市燃氣集團股份有限公司，廣州 深圳 518049； 2.中海石油(中國)有限公司 上海分公司，上海 200335 )

0 引言

煤層氣作為中國常規能源的重要補充，具有重要的開發意義[1-2]。煤層氣儲層具有低滲透率、低壓力及低飽和度的特征[3-4]，需要對其壓裂才能達到經濟開采目的[5]，應用較廣泛的為壓裂直井技術。同時，采用試井技術可以了解儲層物性參數及流體流動特征[6]，在煤層氣開發中應用廣泛[7]。對于煤層氣藏壓裂直井問題，ANBARCI K等[8]建立試井模型，研究擬穩態和非穩態擴散的影響；鄭利[9]研究煤層氣藏的線性流試井模型；曹海濤[10]研究煤層氣藏的對稱雙翼壓裂直井試井模型；ZHAO Y L等[11]考慮縫網建立煤層氣藏復合壓裂直井試井模型。

在進行直井壓裂改造時，受地應力影響，壓開的裂縫一般不是單條裂縫，而是沿井筒向周圍各個方向延伸的多翼裂縫，形成多翼壓裂直井[12]。LUO W J等[13]提出一種半解析方法，建立多翼壓裂直井試井模型，并在煤層氣試井中得到應用。CHEN Z M等[14]研究煤層氣藏多翼壓裂直井試井模型，耦合應力敏感特性的影響。ZHANG L H等[15]耦合壓裂改造區，建立復合煤層氣藏多翼壓裂直井試井模型。這些模型的建立基于煤層氣藏儲層中孔隙裂縫均勻分布，但實際孔隙裂縫復雜、無序[16]，傳統歐幾里得空間下的試井模型無法描述該特征。基于分形理論的分形幾何，由于其自相似性及標度不變性，能較好描述儲層多孔介質的復雜性、無序性，更接近實際[17]。目前，已有研究成果將分形理論應用于煤層氣藏的試井模型[18]，但并沒有關于煤層氣藏有限導流能力多翼壓裂直井試井模型的應用。

基于分形理論，筆者考慮煤層氣儲層復雜、無序的裂縫分布，耦合應力敏感特性，建立分形煤層氣藏多翼壓裂直井試井模型，求解模型得到井底壓力動態曲線。根據曲線特征劃分流動階段，并進行敏感性參數分析，為研究煤層氣藏提供一種參數反演方法。

1 物理模型

煤層氣藏多翼壓裂直井物理模型見圖1。基本參數及假設條件：(1)在壓裂過程中形成以井筒為中心的M條人工裂縫，人工裂縫貫穿整個儲層，長為LF，滲透率為KF，寬度為WF，壓力降方向為從趾部到根部，氣體先流入人工裂縫，再流入井筒；(2)氣井產量為qsc，儲層初始壓力為pi；(3)考慮儲層裂縫分布復雜、無序性，天然裂縫系統視為分形體，基質中氣體向天然裂縫擬穩態擴散；(4)忽略溫度變化、毛管力及重力，為單相氣體滲流。

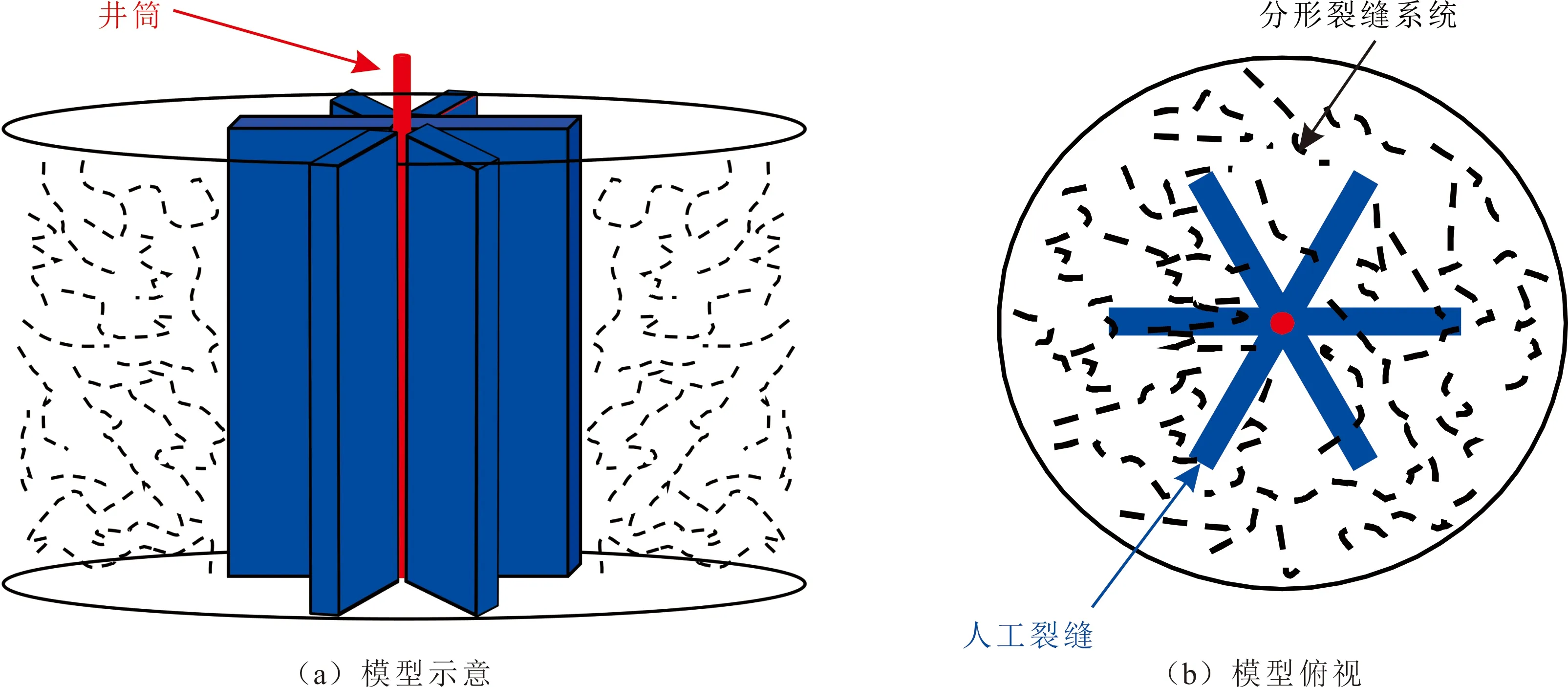
圖1 煤層氣藏多翼壓裂直井物理模型Fig.1 Physical model for multi-wing fractured vertical well in the coalbed methane reservoir

2 數學模型

2.1 模型建立

2.1.1 儲層線源模型

當不考慮天然裂縫分形特征時，結合質量守恒方程、運動方程及狀態方程，得到天然裂縫系統的滲流數學模型為

(1)

式中：r為徑向距離；Kf為天然裂縫系統滲透率；pf為天然裂縫系統壓力；μg為氣體黏度；Z為真實氣體偏差因子；φf為天然裂縫系統孔隙度；t為時間；q*為基質系統向天然裂縫擴散的氣體量。

天然裂縫系統擬壓力Ψf的表達式為

(2)

結合式(2)，對式(1)進行線性化得

(3)

式中：Ctf為天然裂縫系統綜合壓縮系數。

考慮天然裂縫系統的分形特征，引入天然裂縫系統的滲透率kf和孔隙度φf表達式[19]：

(4)

式中：Kfr和φfr分別為參考長度為Lref的天然裂縫系統滲透率和孔隙度；dmf為分形維數，反映天然裂縫系統的無序性和各向異性；d為歐幾里得幾何空間維數，對于徑向系統，取值為2；θ為反常擴散指數。

考慮天然裂縫的應力敏感性，引入按照氣體擬壓力定義的應力敏感因子κp[20]：

(5)

氣體由基質向天然裂縫的擴散量為

(6)

式中：ρgsc為煤層氣密度；Vm為基質中煤層氣體積分數。

將式(4-6)代入式，進行無因次化，得到考慮分形特征的煤層氣藏天然裂縫系統滲流數學模型：

(7)

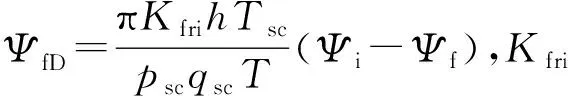
對于基質向天然裂縫擴散的氣體，采用Fick第一定律描述，其無因次形式為

(8)

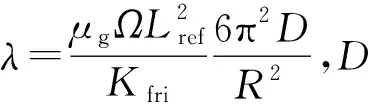
無因次化的初始條件、外邊界條件及內邊界條件分別為

ΨfD|t=0=0;

(9)

ΨfD|r→∞=0;

(10)

(11)

2.1.2 人工裂縫模型

描述第i條人工裂縫內氣體流動的滲流微分方程為

(12)

式中：pFi為第i條人工裂縫的壓力；ξ、χ為人工裂縫坐標。

人工裂縫區域與儲層區域相比很小，可忽略人工裂縫壓縮性，對式(12)進行線性無因次化，得到人工裂縫內氣體滲流微分方程[9]為

(13)

邊界條件為

(14)

(15)

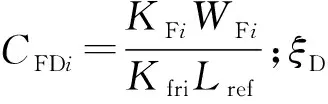
2.2 模型求解

2.2.1 儲層線源模型

考慮應力敏感效應的數學模型非線性較強，經過Pedrosa變換[21]、攝動變換[22]及Laplace變換[23]，得到天然裂縫系統和基質系統數學模型：

(16)

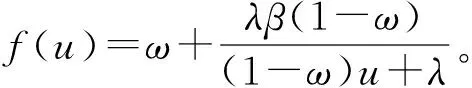
式(16)為廣義貝塞爾方程，其解為

(17)

式中：

(18)

2.2.2 人工裂縫模型

應用Pedrosa變換、攝動變換及Laplace變換，得到拉式空間下的人工裂縫數學模型：

(19)

忽略人工裂縫寬度方向氣體的流動，對式(19)進行二重積分[9]得

(20)

假設與儲層交界面處人工裂縫內壓力與儲層壓力相等，式(20)可寫為

(21)

式(21)表示井底壓力與人工裂縫上任意一點壓力響應差，而儲層任意一點壓力響應可由疊加原理得到，結合儲層線源模型的解，相互耦合，最終求得井底壓力。

3 井底壓力

采用數值離散方法[24]，將每條壓裂裂縫按逆時針方向進行編號，最靠近x軸正方向的人工裂縫編號為1，依次排序，直到編號為M，且第i條人工裂縫與x軸正方向的夾角為θi(見圖2)。將每條人工裂縫離散成N個微元段，每個微元段的長度可由人工裂縫長度計算得到，第i條人工裂縫的第j個微元段的中點坐標可以表示為

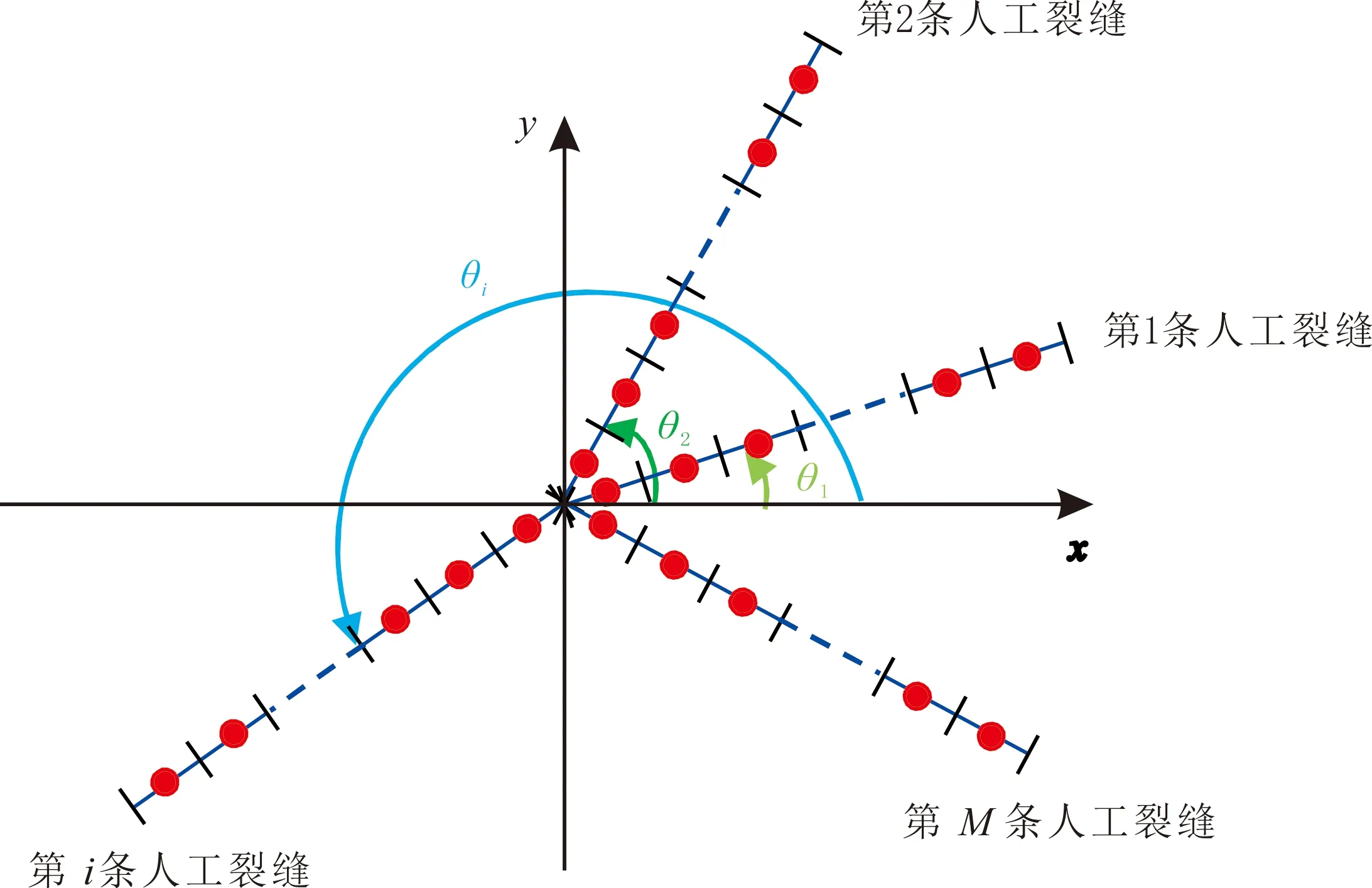
圖2 煤層氣藏多翼裂縫編號示意Fig.2 Schematic of numbering for multi-wing fracture of coalbed methane reservoir

(22)

式中：LFi為第i條人工裂縫長度；ΔLFi,j為第i條人工裂縫的第j個微元段長度。

根據疊加原理，儲層任意一點的壓力響應由所有微元段在該點形成的壓力響應疊加而得：

(23)

由徑向坐標與直角坐標的關系，式(23)可以寫為關于直角坐標的積分：

(24)

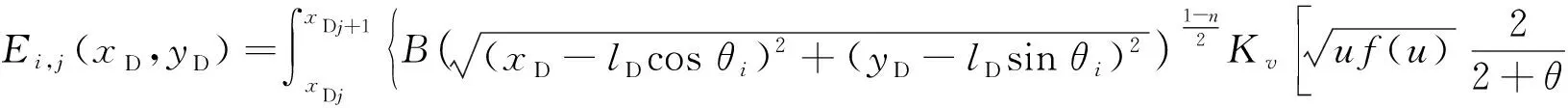
對于人工裂縫上任意一點可以取微元段的中點，則

(25)

對于第a條人工裂縫的第b個微元段，化簡式(25)可得

(26)

取所有微元段中點，根據式(26)得到M×N個線性方程組，但未知數有M×N+M+1個，由流量關系可以得到另外兩個限制條件。

每條人工裂縫的微元段產量和等于該條人工裂縫的產量：

(27)

所有人工裂縫的產量和等于生產井的產量：

(28)

從而構成M×N+M+1維線性方程組：

AX=B,

(29)

式中：A、B為方程組系數矩陣。

求解式(29)得到拉式空間下井底壓力，進而得到真實空間下的井底壓力和產量。根據杜哈美疊加原理[25]，得到考慮井筒儲集效應和表皮效應的井底壓力為

(30)

式中：S為量綱一的表皮因數；CD為量剛一的井筒儲集系數。

對拉式空間下的井底壓力解進行Stehfest數值反演[26]，得到真實空間下的井底壓力解。

4 模擬結果

4.1 典型曲線特征

繪制分形煤層氣藏有限導流多翼壓裂直井壓力動態曲線(見圖3)。根據壓力導數曲線特征，將壓力動態曲線劃分為9個流動階段：(1)井儲效應；(2)表皮效應；(3)雙線性流，存在儲層氣體垂直流入人工裂縫和人工裂縫氣體流入井筒兩種線性流，考慮分形特征的壓力導數曲線斜率大于；(4)儲層線性流，儲層氣體垂直流入人工裂縫，考慮分形特征的壓力導數曲線斜率大于；(5)人工裂縫干擾，垂直流入人工裂縫的氣體產生干擾，導數曲線呈現一個淺駝峰；(6)過渡流；(7)天然裂縫第一徑向流，考慮分形特征的壓力導數不是一條水平線，呈斜線；(8)竄流，基質系統吸附的煤層氣逐漸解吸出來擴散運移進入天然裂縫系統，壓力導數曲線存在“凹子”；(9)儲層第二徑向流，基質與天然裂縫系統氣體運移達到動態平衡，但考慮分形特征的壓力導數曲線不再是一條水平線，呈斜線。

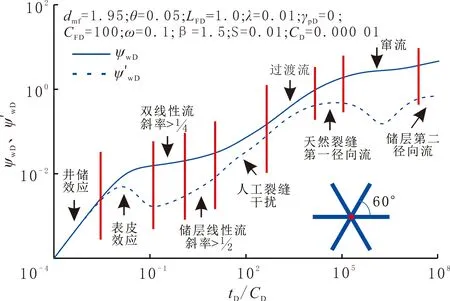
圖3 分形煤層氣藏有限導流多翼壓裂直井壓力動態曲線Fig.3 Dynamic pressure curve for multi-wing fractured vertical well with finite conductivity in the fractal CBM reservoir

4.2 參數敏感性分析

4.2.1 質量分形維數和反常擴散指數

質量分形維數dmf與反常擴散指數θ對壓力動態曲線的影響較大(見圖4-5)，主要表現在試井曲線的前中期(雙線性流、儲層線性流、人工裂縫干擾階段)及后期(天然裂縫第一徑向流、竄流、儲層第二徑向流階段)。質量分形維數越小，前中期的壓力和壓力導數曲線位置越低，后期二者的位置越高(見圖4)。反常擴散指數與之相反，隨反常擴散指數增加，前中期曲線位置越低，后期位置越高(見圖5)。二者的變化并不改變各流動階段的出現時間。

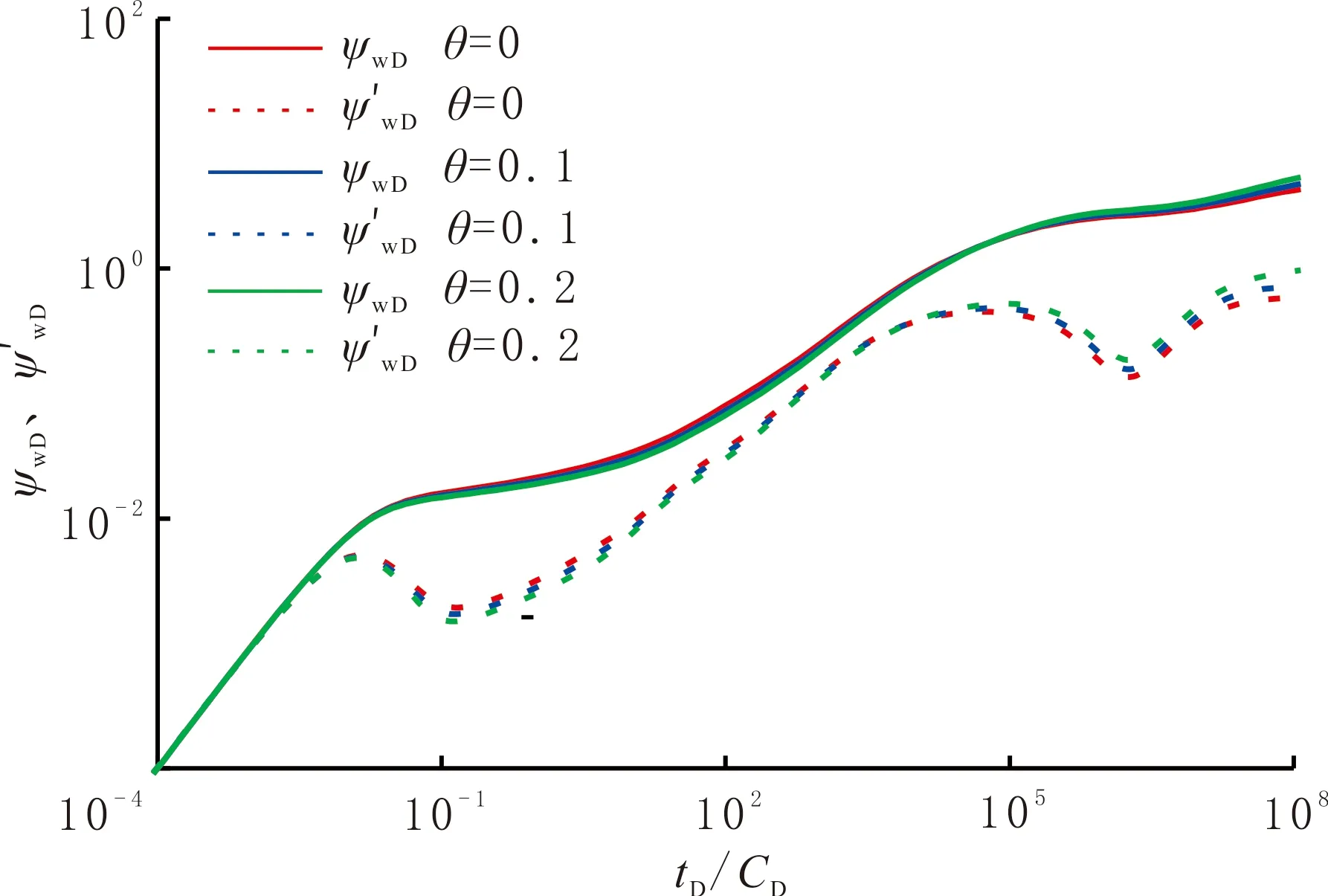
圖5 反常擴散指數對壓力動態曲線的影響Fig.5 The influence of anomalous diffusion index on dynamic pressure curve

4.2.2 人工裂縫條數

人工裂縫條數M對壓力動態曲線的影響見圖6。由圖6可以看出，隨人工裂縫條數的增加，前中期(雙線性流、儲層線性流、人工裂縫干擾階段)階段的壓力和壓力導數曲線整體位置降低。這是由于人工裂縫越多，壓裂改造程度越大，氣體更容易產出，所需生產壓差較小；隨人工裂縫條數的增加，干擾越容易發生，人工裂縫干擾階段的淺駝峰越明顯，且出現得越早，儲層線性流持續時間變短，甚至被掩蓋。

圖6 人工裂縫條數對壓力動態曲線的影響Fig.6 The influence of number of artificial fractures on dynamic pressure curve

4.2.3 人工裂縫長度

隨人工裂縫長度的增加，整個壓裂改造范圍擴大，形成的泄流區域面積越大，氣體流動需要的能量損耗變小。人工裂縫長度LFD對壓力動態試井曲線的影響見圖7。由圖7可以看出，LFD越大，整個雙線性流、線性流及人工裂縫干擾階段的壓力及壓力導數曲線位置越低，雙線性流階段持續時間變長，線性流階段持續時間變短。

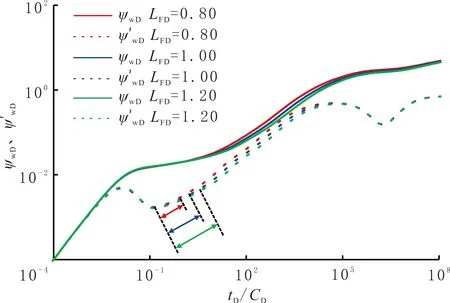
圖7 人工裂縫長度對壓力動態曲線的影響Fig.7 The influence of length of artificial fracture on dynamic pressure curve

4.2.4 人工裂縫角度

人工裂縫角度越小，干擾階段的壓力及壓力導數曲線位置越高，并且干擾階段出現得越早，同時掩蓋儲層線性流階段(見圖8)。這是由于裂縫角度越小，相鄰裂縫靠得更近，干擾越容易發生且干擾程度更大，導致整個生產中能量損耗變大。

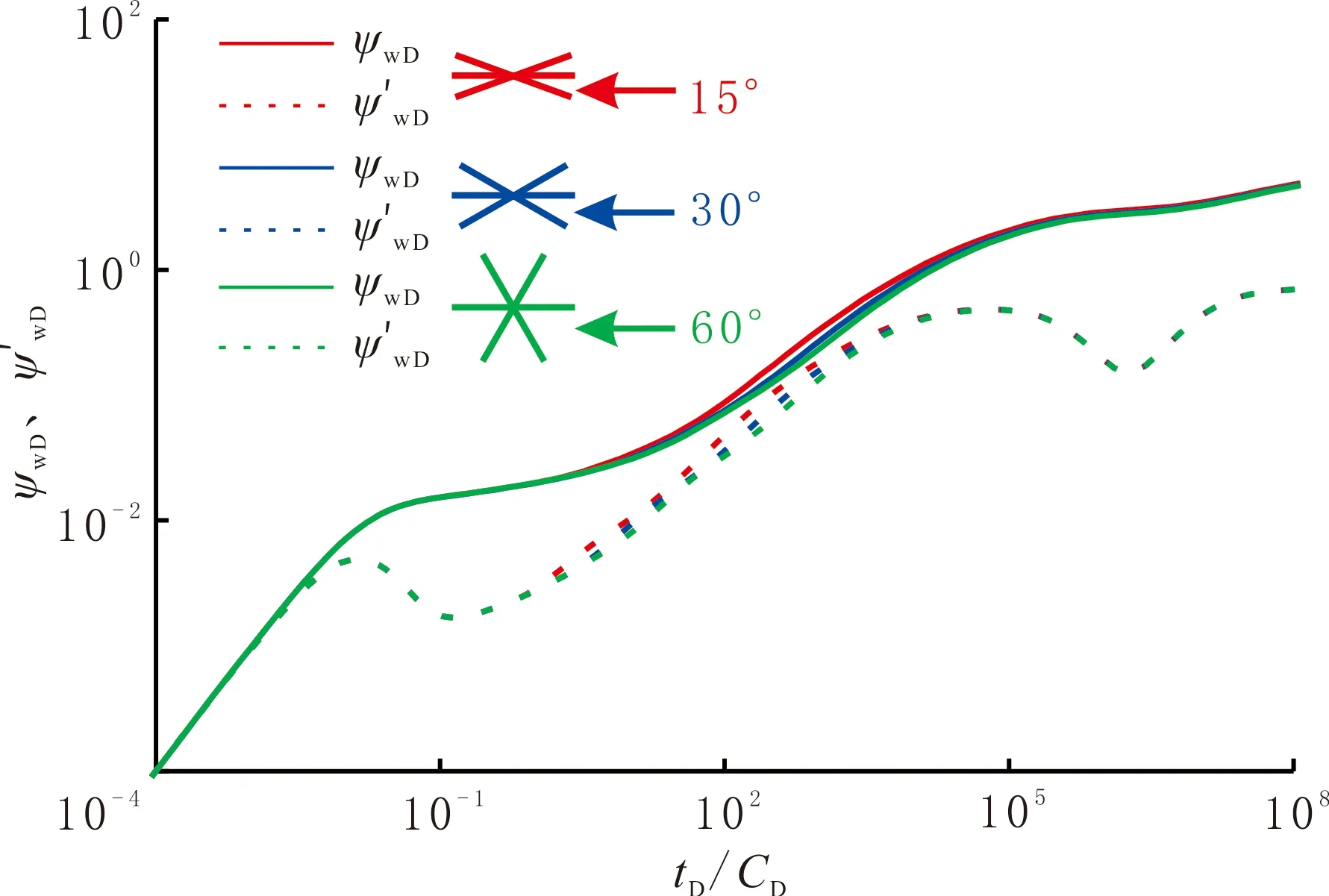
圖8 人工裂縫角度對壓力動態曲線的影響Fig.8 The influence of angle of artificial fracture on dynamic pressure curve

4.2.5 人工裂縫導流能力

人工裂縫導流能力CFD對壓力動態曲線的影響見圖9。由圖9可以看出，隨人工裂縫導流能力的增加，雙線性流階段的持續時間變短，儲層線性流階段的持續時間變長。若導流能力大到一定程度、近似無限大導流能力時，雙線性流階段被掩蓋，只剩儲層線性流階段。

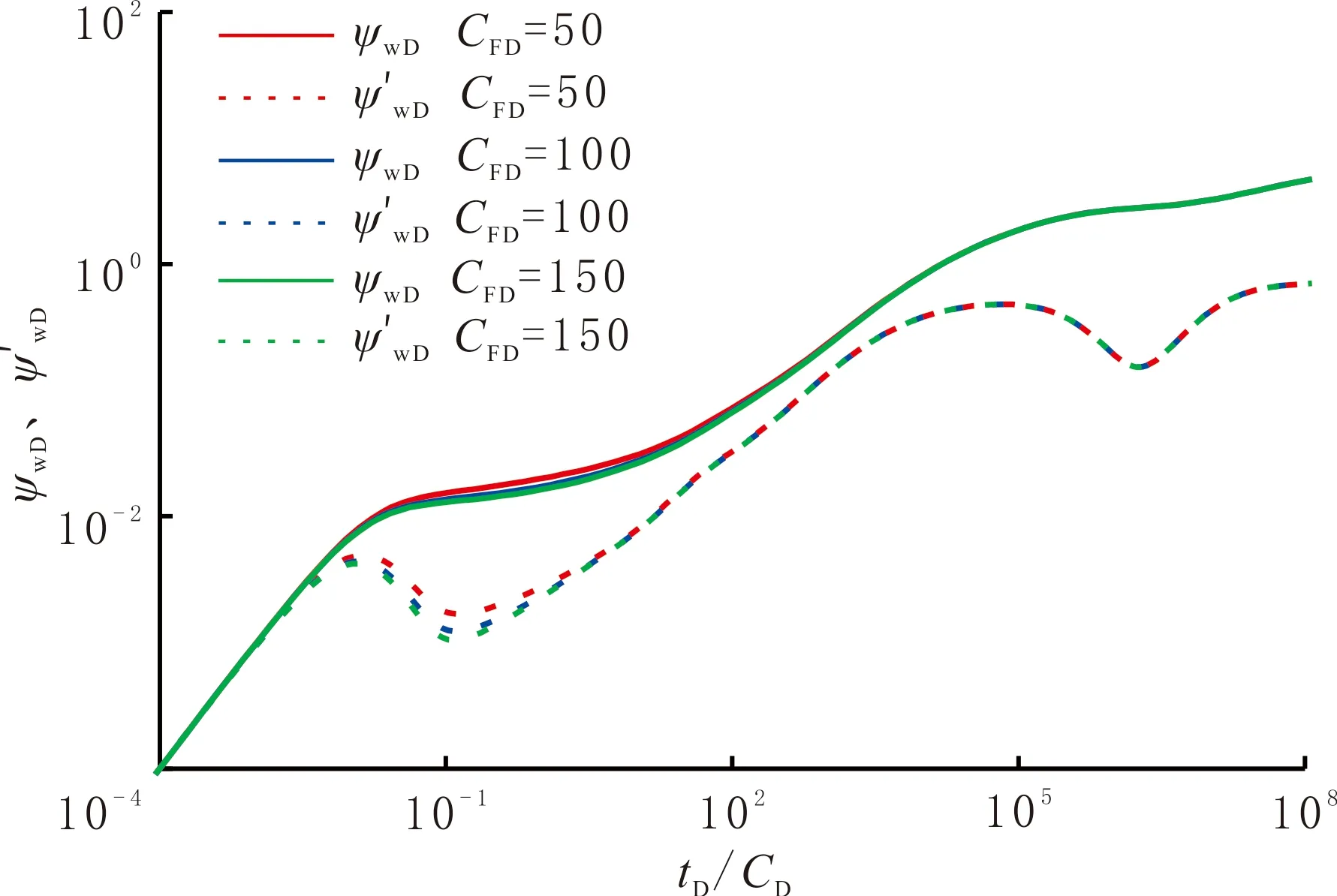
圖9 人工裂縫導流能力對壓力動態曲線的影響Fig.9 The influence of conductivity of artificial fracture on dynamic pressure curve

4.2.6 應力敏感因子

隨應力敏感因子γpD的增加，后期壓力及壓力導數曲線位置升高(見圖10)。這是由于生產壓差降低到一定程度時，應力敏感效應才明顯體現，應力敏感因子越大，整個儲層滲透率降低越大，導致氣體流動阻力增加，能量損耗大，不利于壓裂生產。

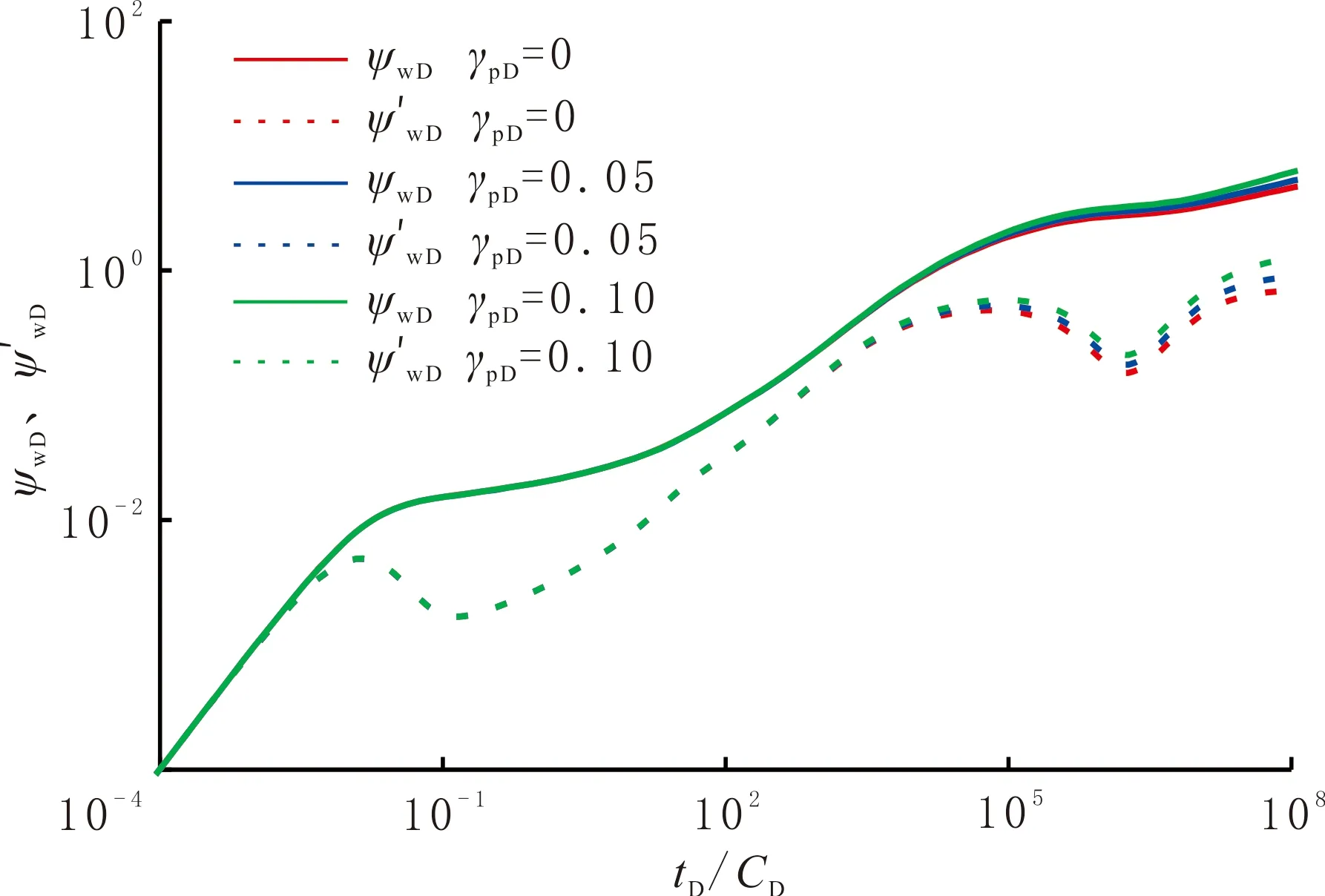
圖10 應力敏感因子對壓力動態曲線的影響Fig.10 The influence of stress sensitivity factor on dynamic pressure curve

5 結論

(1)考慮煤層氣儲層復雜、無序及非均質性，應用分形理論建立有限導流多翼壓裂直井試井模型，通過數值離散方法和疊加原理等求解模型，并繪制典型井底壓力圖版。

(2)根據曲線特征劃分為9個流動階段：井儲效應、表皮效應、雙線性流、儲層線性流、人工裂縫干擾、過渡流、天然裂縫第一徑向流、竄流和后期儲層第二徑向流階段。與傳統試井曲線相比，曲線位置和斜率發生變化。

(3)質量分形維數和反常擴散指數對壓力動態曲線的前中期和后期影響較大，二者的影響規律相反；人工裂縫條數、長度、角度及導流能力對壓力動態曲線的影響主要體現在中期的雙線性流、儲層線性流及人工裂縫干擾階段；應力敏感因子主要影響曲線后期，其增加導致壓力和壓力導數曲線位置上升。