三區(qū)間復(fù)合型第一種Weber 方程邊值問題求解的新方法

何 簽，李順初，董曉旭，夏 星，彭 春

（西華大學(xué) 理學(xué)院，四川 成都610039）

許多物理、化學(xué)、工程、生物中抽象出的數(shù)學(xué)模型可以轉(zhuǎn)化為微分方程邊值問題［1］，可見微分方程邊值問題求解的重要性。針對不同的微分方程（組），其解的結(jié)構(gòu)表達式也呈現(xiàn)出復(fù)雜性和多樣性，因而微分方程（組）解的相似結(jié)構(gòu)思想開始形成。李順初［2－4］等分別對二階線性常微分方程（組）的解進行探究，并提出了化解為統(tǒng)一的結(jié)構(gòu)式的新方法——相似構(gòu)造法。此方法可運用于Weber 方程［5－7］、Hermite 方程［8］、歐拉超幾何方程［9］、復(fù)合變型Bessel 方程［10］、復(fù)合Bessel 方程［11］、復(fù)合Thomson 方程［12］及石油工程所涉及的滲流方程［13－15］中。

第一種Weber 方程是特殊函數(shù)重點研究的內(nèi)容之一［16］，它在諸多重要學(xué)科（如流體力學(xué)、物理學(xué)等）中的應(yīng)用極為廣泛［6］。在量子力學(xué)中考慮一維諧振子問題時，可通過對定態(tài)Schr?dinger 方程的變量進行代換，將其轉(zhuǎn)換為第一種Weber 方程求解［17］，可見研究第一種Weber 方程的邊值問題是很有必要的。文獻［6－7］闡述了第一種Weber 方程和二區(qū)復(fù)合第一種Weber 方程的求解及應(yīng)用，但卻沒有對三區(qū)復(fù)合第一種Weber 方程的解進行研究。為了進一步地探討第一種Weber 方程的相關(guān)理論，本文研究如下三區(qū)復(fù)合第一種Weber 方程邊值問題

其中：x所在區(qū)間均為閉區(qū)間；D，E，F(xiàn)，M，N，a，b，c，d，λ1，λ2，μ1，μ2是常數(shù)；ni(i＝1，2，3) 是整數(shù)，且ni(i＝1，2，3) ≥1，λ1λ2μ1μ2≠0，M2＋N2≠0，D≠0，0 ＜a＜b＜c＜d。

1 預(yù)備知識

其中：i＝1 代表內(nèi)區(qū)(a≤x≤b)，i＝2 代表中區(qū)(b≤x≤c)，i＝3 代表外區(qū)(c≤x≤d)。

2 主要定理及其證明

定理1如果邊值問題（1）有唯一解，則其內(nèi)區(qū)、中區(qū)、外區(qū)解分別表示為

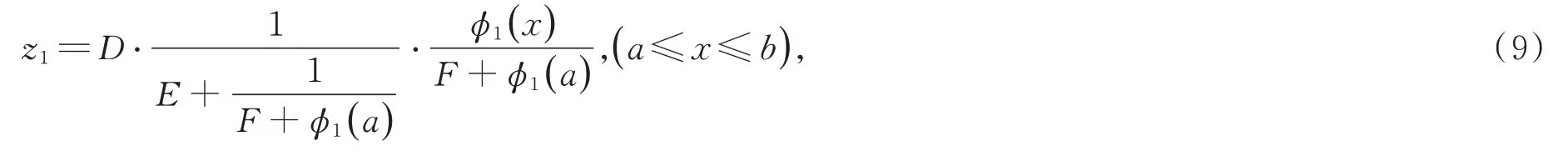
將（17）—（22）式組成一個關(guān)于待定系數(shù)A1，B1，A2，B2，A3，B3的線性方程組，結(jié)合（5）—（8）式，求得關(guān)于A1，B1，A2，B2，A3，B3的系數(shù)行列式為

3 相似構(gòu)造法的步驟

第二步為內(nèi)、中、外區(qū)相似核函數(shù)的構(gòu)造。外區(qū)引解函數(shù)和外邊界條件系數(shù)M，N 構(gòu)成外區(qū)相似核函數(shù)，即式（12），同時算出?3(c)；中區(qū)引解函數(shù)、銜接條件系數(shù)μ1，μ2及?3(c) 構(gòu)成中區(qū)相似核函數(shù)，即式（13），同時算出?2(b)；內(nèi)區(qū)引解函數(shù)、銜接條件系數(shù)λ1，λ2及?2(b) 構(gòu)成內(nèi)區(qū)相似核函數(shù)，即式（14），同時算出?1(a)。

第三步為邊值問題（1）的解的獲得。內(nèi)邊界條件系數(shù)D、E、F，內(nèi)區(qū)相似核函數(shù)及?1(a) 構(gòu)成內(nèi)區(qū)解，即式（9）；內(nèi)邊界條件系數(shù)D、E、F，銜接性條件系數(shù)λ1、λ2，內(nèi)區(qū)引解函數(shù)，中區(qū)相似核函數(shù)及?2(b) 構(gòu)成中區(qū)解，即式（10）；內(nèi)邊界條件系數(shù)D、E、F，銜接性條件系數(shù)λ1、λ2、μ1、μ2，內(nèi)區(qū)與中區(qū)引解函數(shù)，外區(qū)相似核函數(shù)及?2(b)、?3(c) 構(gòu)成外區(qū)解，即式（11）。

4 相似構(gòu)造法的應(yīng)用

5 結(jié)論與認識

（1）相似構(gòu)造法是求解邊值問題（1）的一種簡潔、準確、思路清晰的方法，只需找到第一種Weber 方程的2 個線性無關(guān)的解，并構(gòu)造出相似核函數(shù)，再結(jié)合邊界條件、銜接條件系數(shù)進行組裝，邊值問題（1）的解即可獲得。

（2）相似構(gòu)造法能夠提升求解邊值問題（1）的計算速度，以便能快速得到此類邊值問題的解的相似結(jié)構(gòu)。

（3）經(jīng)過研究發(fā)現(xiàn)，當(dāng)改變邊界條件、交界面銜接條件系數(shù)時，邊值問題（1）的解仍然呈現(xiàn)出相似結(jié)構(gòu)，這更加說明了相似構(gòu)造法在實際應(yīng)用中的實用性和美觀性。