換熱單元面積費用指數松弛策略優化換熱網絡

金 艷，崔國民，蔣 瑜，趙倩倩，張冠華

（上海理工大學 能源與動力工程學院 新能源與科學研究所上海市動力工程多相流動與傳熱重點實驗室，上海 200093）

換熱網絡綜合（HENS）以最大的能量回收或最小的年綜合費用（TAC）為優化目標［1］。換熱網絡優化方法中，同步優化法［2］主要包括確定性方法［3］和啟發式方法［4］。確定性方法有分支界定法［5］、外部逼近法［6］、極大值極小值法［7-8］等，這類方法有較高的計算精度，但對初始點依賴性較高，易陷入局部最優。啟發式方法進化機制相對簡單，在有限空間內，能夠迅速解決問題，包括遺傳算法［9-10］、模擬退火算法［11-12］、粒子群算法［13］、微分進化算法［14-15］等。于盛男等［16］提出以換熱單元數為導向的接受差解概率策略，提高算法的全局搜索能力；朱玉雙等［17］通過限制參與進化的換熱單元數，增強了后期精細搜索能力，使得算法具有良好的持續性；蘇戈曼等［18］基于節點非結構模型，通過分析換熱單元生成幾率和個數對網絡的影響，提出動態調整換熱單元生成參數，提高優化效率；鄧煒棟等［19］分析了換熱單元生成、消去障礙，提出固定投資費用松弛策略，引導有結構進化障礙的換熱單元生成和消去。上述改進方法均是從影響換熱單元個數的角度對問題進行處理以增強結構進化能力，一定程度上強化了算法全局搜索能力，但對問題優化效果有限。換熱網絡優化過程中，存在固定結構，換熱單元數和熱冷流體匹配關系很難發生改變，TAC下降趨勢逐漸平緩，個體很容易陷入停滯狀態，嚴重影響算法優化效率。面積費用指數作為冪數項，指數的變化可改變整型變量和連續變量優化路徑，增加個體向其他潛力方向優化的可能性，同時為便于在更大可行域內搜索較好解，放松面積費用指數對目標函數的約束，減小目標函數優化的壓力，提出換熱單元面積費用指數松弛策略（松弛即在變量可變化范圍內，根據條件變化采取調整，降低優化變量對目標函數的緊張程度，放松約束，使目標函數獲得最佳求解方案）。

本工作在優化陷入停滯狀態時選取部分換熱量不為零的換熱單元參與松弛，通過換熱器和公用工程主輔協同松弛來保持連續變量持續優化，增強結構變異能力，最后通過2 個算例驗證改進策略的有效性。

1 換熱網絡優化數學模型

1.1 問題描述

采用節點非結構模型，包含熱流體和冷流體，每股流體均設置一定數量節點，通過隨機方式選取熱冷節點形成匹配。

熱、冷流體的總節點數由式（1）和式（2）計算。

式中，UH為熱節點數；UC為冷節點數；NH為熱流體股數；NC為冷流體股數；GBH為熱節點總數；GBC為冷節點總數。

同時，網絡中熱、冷節點編號需滿足式（3）和式（4）。

式中，nH為熱流體節點編號，nH=1，2，…，UH；nC為冷流體節點編號，nC=1，2，…，UC；nkH為網絡中熱節點編號，nkH=1，2，…，GBH；nkC為網絡中冷節點編號，nkC=1，2，…，GBC；i，j分別為熱、冷流體編號。

圖1 為換熱網絡非結構模型。由圖1 可知，該網絡隨機生成4 個換熱單元（2 股熱流、2 股冷流），流體末端設置冷熱公用工程。

圖1 換熱網絡非結構模型Fig.1 A non-structural model of heat ecxchanger networks.

1.2 目標函數

換熱網絡的目標函數是TAC 最小，表達式見式（5）。

式中，CHU，CCU分別為熱、冷公用工程量的費用系數；CFHU，CFCU，CFHE分別為熱、冷公用工程及換熱器的固定投資費用系數；分別為熱、冷公用工程及換熱器面積費用系數；QHUj，QCUi分別為熱、冷公用工程用量，kW；Z，Zi nH分別為冷、熱公用工程與熱節點處換熱器存在與否的0 ～1 變量；β為面積費用指數；A為換熱面積，m2。

1.3 約束條件

每股流體上的熱平衡計算見式（6）和式（7）。

式中，與分別為流股經過換熱器的進口與出口溫度，℃；W為熱容流率，kW/℃；Qi nH為第i股熱流體上第nH個節點處換熱器換熱量，kW；Qj nC為第j股冷流體上第nC個節點處換熱器換熱量，kW。

冷、熱公用工程的熱平衡計算見式（8）和式（9）。

溫度可行性約束條件見式（10）和式（11）。

最小溫差約束條件見式（12）～（17）。

式中，ΔTmin為最小傳熱溫差，℃。

每次新生成的換熱單元應避免與當前網絡中已存在的換熱單元重合，因此每次選取的節點編號不重合，且滿足式（18）和式（19）。

式中，QnkHnew，QnkCnew為新生換熱單元換熱量，kW；nkHnew，nkCnew為新生換熱單元熱、冷流體節點編號。

2 強制進化隨機游走算法

本工作采用強制進化隨機游走（RWCE）算法中的節點非結構模型，每個結構初始不存在任何換熱匹配，通過熱、冷節點的隨機匹配產生新的換熱器，經隨機游走、選擇和變異操作，滿足終止條件即停止。RWCE 優化節點非結構模型具體流程如下。

1）種群初始化

種群中包含N個個體，初始時不進行任何換熱匹配，僅依靠冷、熱公用工程達到目標溫度。

2）存在的換熱匹配進化

對每個個體中匹配的換熱量（Qn kit）隨機游走，設置換熱量最小值消去換熱器。進化公式如式（20）所示。

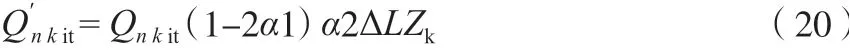
式中，r1 為0 ～1 之間均勻分布的隨機數；Qmin為設置的最小換熱量，kW；Q′′n kit為參與進化后換熱量，kW；若隨機游走后該位置的換熱器被消去，則消去位置的冷、熱節點編號也為零。

3）生成新的換熱匹配

個體進化后，若節點上仍有未生成換熱單元的位置，則按式（23）新生換熱單元。

式中，Qmax為新生換熱單元的最大換熱量，kW；γ為新生成幾率；r2 為0 ～1 之間均勻分布的隨機數。

4）選擇與變異

若個體游走后TAC 小于當前TAC，則保留游走后的結構，將此次游走后的結構作為下一次迭代的初始結構，若個體游走后的費用沒有減小，則以小概率（δ）接受差解。

式中，Nk為換熱網絡中總的換熱器數；Qnit為第n個個體隨機游走前的解，Qnit+1表示下一次迭代初始解。

5）終止條件

若迭代步數滿足：迭代步數不小于最大迭代步數，則迭代停止。

3 換熱單元面積費用指數松弛策略

RWCE 算法由于面積費用指數、對數溫差以及流體匹配關系等因素導致了換熱網絡的非線性。而面積費用指數為冪函數，種類多且性質規律不一，指數的大小就對優化目標函數影響較大，決定了圖像上凸的程度，遠離還是靠近縱坐標。

3.1 換熱單元面積費用指數分析

根據換熱網絡實際情況，分析換熱單元面積費用指數（大于1 和小于1）對RWCE 優化過程的影響。表1 為算例1（以15 股流體（8 股熱流、7 股冷流）為例，簡稱15SP）的流體參數。設置優化參數為：N=1，UH=20，UC=20，ΔL=100 kW，ψe=0.5，Qmin=5 kW，γ=0.1，Qmax=90 kW，δ=0.01。其中，換熱單元費用按8 000+500A0.75計算，單位為$/（m2·a）；取熱公用工程費用為80 $/（kW·a），冷公用工程費用為10 $/（kW·a）。

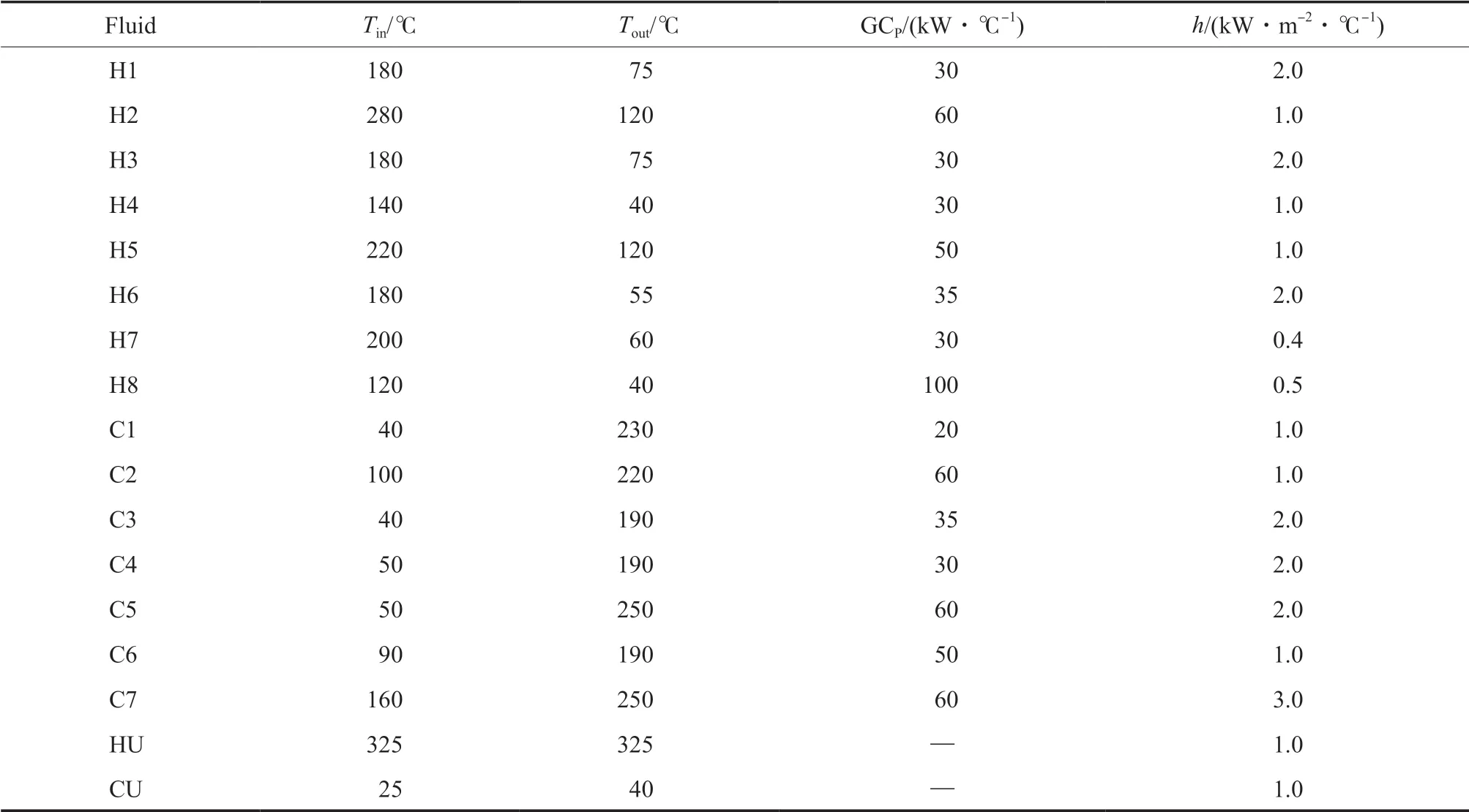
表1 算例1 的流體參數Table 1 The fluid parameters of Case 1

換熱網絡以最小TAC 為優化目標，通過費用變化可反映出優化效率和質量；本工作通過觀察TAC 下降和換熱器數的變化情況來分析它們對面積費用指數大小的影響。圖2 為采用算例1 時不同面積費用指數下換熱器數對比及TAC 下降曲線。通過給定面積費用指數（大于1.0，等于0.5）與原始算例進行比較，記錄各面積費用指數下的換熱器數和TAC 值。由圖2 可知，隨著面積費用指數不同，TAC 存在較大差異，且換熱器數也呈現出不同的變化態勢。當面積費用指數大于1.0 時，需要的換熱器較多，TAC 較高；此時，要使得費用有所下降，系統會通過增加換熱器的方式減小費用，會出現較多換熱量小的換熱器。而當面積費用指數小于1.0時，所需費用則明顯下降，此時可通過減少換熱器來降低費用，可能會出現一股流體上一個換熱器換熱潛能過多；同時換熱器的變化也會引起公用工程的變化，造成換熱器和公用工程數目極度不平衡的情況，浪費資源。

圖2 采用算例1 時不同面積費用指數下換熱器數對比（a）及TAC 下降曲線（b）Fig.2 Comparison of the number of heat exchangers(a) and the decline curves on annual comprehensive cost(TAC)(b)under different area cost indexes when using Case 1.

3.2 換熱單元面積費用指數松弛策略

換熱單元面積費用指數單純增大或減小對TAC 和換熱器數影響較大，會造成TAC 和換熱器數突變，破壞了實際應用中結構的穩定性，為了平衡換熱器和公用工程，保證目標函數的連續性，使TAC 可以繼續下降，將換熱器面積費用指數和公用工程面積費用指數分開處理。本工作采用增大換熱器面積費用指數、減小公用工程面積費用指數的方式。設備運行費用是指以換熱器和公用工程為換熱單元在系統運行過程中產生的必然投資費用，只有二者的費用協同實現增減，才能高效優化換熱網絡。即改變換熱器運行費用對TAC 產生影響的程度需用公用工程來抵消，換熱網路中換熱器數一般多于公用工程數，對換熱器面積費用指數效果進行主要增強，公用工程面積費用指數效果輔助配合，才能使TAC 下降的同時促進結構變化。若優化后期換熱器面積費用指數大于1、公用工程費用指數小于1，可能存在系統解瞬時變差的情況，要使優化向積極方向進行，換熱器數和公用工程數會發生變化，引導換熱網絡向其他潛力方向發展，給予換熱網絡擾動，更有利于合理分配換熱潛能，使系統穩定、可靠運行，保證系統可以有較長的運行年限，降低成本。對于換熱網絡結構，各換熱單元之間存在相互制約關系，只有少數換熱單元變化，才會影響算法局部搜索能力，所以不能對所有換熱單元進行面積費用指數主輔松弛，否則會造成大量無效優化，浪費時間。同時在優化過程中擾動過于頻繁，會破壞連續變量的優化，因此設置TAC 停滯迭代步數值（ITTmax），即TAC 停滯步數大于設定值ITTmax，則隨機抽取部分換熱量不為零的換熱單元對面積費用指數進行松弛，將換熱器面積費用指數乘以一個大于1 的松弛因子，公用工程面積費用指數乘以一個小于1 的松弛因子，其他換熱單元不變，否則仍按原來路徑進行優化。

同樣選取15SP 算例，設參數ITTmax=104，其余參數保持不變，算法改進前后換熱器數對比如圖3 所示。

圖3 算法改進前后換熱器數對比Fig.3 Contrastive structure tends before and after improvement.

由圖3 可知，前期優化策略的加入加速換熱器數波動，擴大可變化的范圍，后期改進策略在原算法不變的情況下仍能繼續結構更新，跳出局部極值。主要是因為改進策略在優化陷入停滯時對固定結構進行干擾，一定程度上打破原有換熱單元之間的約束，對換熱器和公用工程不同程度松弛，網絡會基于目標函數的最優化重新分配換熱器和公用工程，改變了換熱單元進化的方向，增加了換熱單元向其他位置進化的可能性，激發換熱網絡整體活力，增強結構變異能力。

4 算例驗證

4.1 算例1 的驗證

為驗證改進策略的有效性，采用上述15SP算例1 進行分析，具體物流參數見表1。分別用RWCE 算法和改進策略應用于算例1，結果見圖4。改進策略對隨機抽取到的換熱器設置換熱器面積費用指數松弛1.34 倍，公用工程面積費用指數松弛0.1 倍，其他優化參數不變。由圖4 可知，RWCE 算法TAC 為1 529 020 $/a，改進策略TAC為1 518 968 $/a，費用下降了10 052 $/a。首先兩種算法換熱單元數不同，RWCE 算法得到10 個換熱器、10 個公用工程，改進策略得到10 個換熱器、9 個公用工程。其次換熱器和公用工程位置也不同。就第三股熱流（H3）來說，改進前該流體只有1個換熱器，改進后有3 個換熱器，由于改進策略換熱器面積費用指數大于1，要使目標函數連續，系統會重新分配換熱潛能，避免因面積費用指數的改變導致TAC 突變；第四股熱流（H4）不采用松弛策略有1 個換熱器、1 個公用工程，采用松弛策略后該流體的所有換熱潛能由公用工程承擔，面積費用指數大于1，換熱器對應的設備運行費用升高，需要公用工程面積費用指數小于1 的輔助使TAC下降，因此該流體不匹配換熱器。說明采用換熱單元面積費用指數松弛策略對換熱網絡進行優化，引導連續變量優化的同時促進了結構變異，得到了性能更優的網絡結構。

圖4 采用RWCE 算法得到的結構圖（a）和采用改進策略得到的結構圖（b）Fig.4 Structure diagram obtained by RWCE algorithm(a) and improved strategy(b).

4.2 算例2 的驗證

表2 為算例2（以10 股流體（7 股熱流、3 股冷流）為例，簡稱10SP）的流體參數。設置優化參數N=2，UH=30，UC=30，ΔL=100 kW，ψe=0.5，Qmin=5 kW，γ=0.1，Qmax=90 kW，δ=0.01，ITTmax=103。換熱器面積費用指數松弛1.1 倍，公用工程面積費用指數松弛0.2 倍。其中，換熱單元費用按300A計算，單位為$/（m2·a）；取熱公用工程費用為60 $/（kW·a），冷公用工程費用為5 $/（kW·a）。

表2 算例2 的流體參數Table 2 The fluid parameters of Case 2

分別將RWCE 算法和改進策略應用于算例2，結果見圖5。

圖5 采用RWCE 算法得到的結構圖（a）和采用改進策略得到的結構圖（b）Fig.5 Structure diagram obtained by RWCE algorithm(a) and improved strategy(b).

由圖5 可知，RWCE 算法TAC 為8 716 700$/a，改進策略TAC 為8 702 421 $/a，費用下降了14 279 $/a。采用改進策略得到的換熱器數明顯多于RWCE 算法，除第一股熱流（H1）溫位較高都未匹配換熱器，2，4，5，6，7 股熱流（H2，H4，H5，H6，H7）松弛后的換熱器增加，一些換熱量較小的換熱器生成，同時公用工程數也減少了1 個，所以采用改進策略極大提升了結構變異能力，引導個體向更具潛力方向發展，再次驗證了改進策略的有效性。

5 結論

1）換熱單元面積費用指數作為設備運行費用的冪數項，可以較大程度決定TAC 下降空間。若換熱單元面積費用指數發生改變，目標函數TAC圖像會突然靠近或遠離縱坐標，使得整型變量和連續變量優化頻率增加，有助于增強結構變異能力，但不利于連續變量的持續優化。

2）提出換熱單元面積費用指數松弛策略，將換熱器面積費用指數和公用工程面積費用指數分開處理，換熱器面積費用指數大于1，公用工程面積費用指數小于1，以換熱器面積指數松弛為主、公用工程面積指數松弛為輔協同優化換熱網絡，增強個體競爭活力，促進TAC 繼續下降的同時強化個體變異能力。

3）采用15SP 和10SP 算例驗證，均得到較好的優化結果，表明該策略改進的有效性，提升了算法的優化性能。

符 號 說 明

h 換熱系數，(kW·m2)/℃ΔL 個體的最大游走步長N 流體編號NC 冷流體股數NH 熱流體股數Nk 換熱網絡中總的換熱器數nC 冷流體節點編號，nC=1，2，…，UC nH 熱流體節點編號，nH=1，2，…，UH nkC 網絡中冷節點編號，nkC=1，2，…，GBC nkH 網絡中熱節點編號，nkH=1，2，…，GBH nkH new，nkC new 新生換熱單元熱、冷流體節點編號QHU j，QCU i 熱、冷公用工程用量，kW Qi nH 第i 股熱流體上第nH 個節點處換熱器換熱量，kW Qj nC 第j 股冷流體上第nC 個節點處換熱器換熱量，kW Qmax 新生換熱單元的最大換熱量，kW Qmin 設置的最小換熱量，kW QnkH new，QnkC new 新生換熱單元換熱量，kW Qn it 第n 個個體隨機游走前的解Qn it+1 下一次迭代初始解Q′′n k it 參與進化后換熱量，kW Qn k it，Q′n k it 個體游走前后第k 個換熱器換熱量，kW T 溫度，℃ΔTmin 最小傳熱溫差，℃UC 冷節點數UH 熱節點數W 熱容流率，kW/℃Z，Zi nH 冷、熱公用工程與熱節點處換熱器存在與否的0 ～1 變量Zk 0-1 變量，由ψe 決定α1，α2，r1，r2 0 ～1 之間均勻分布的隨機數β 面積費用指數γ 新生成幾率ψe 進化幾率角標i，j 熱、冷流體編號

in，out 進口和出口