1 500 MPa超高強馬氏體鋼回彈影響因素分析

郭 龍，張夢鴿，劉東海，李彥波，徐 鋒，武春虎，張 政，劉利剛，*

(1.凌云工業股份有限公司，河北 保定 071000；2.河北省汽車安全件工程技術研究中心，河北 保定 071000；3.燕山大學 機械工程學院，河北 秦皇島 066004)

0 引言

隨著汽車輕量化的發展，吉帕級超高強鋼在車身結構上的應用日益廣泛。特別是汽車加強件、門檻及防撞梁等安全結構件強度已經達到1 500 MPa。鋼材強度的提高會嚴重影響到其自身的彎曲回彈性能，加大了冷彎成型、冷沖壓等成型工藝難度[1-5]，原有1 000 MPa以下級別材料的回彈控制工藝也無法適用。因此，針對1 500 MPa超高強度鋼彎曲回彈性能的研究，可為冷彎成型、冷沖壓等成型工藝提供有效的數據參考。根據彎曲回彈性能進行成型工藝設計，可以有效地提高設計質量，對整個超高強鋼的成型工藝研究都十分有價值。

紀登鵬等[6]先后進行了單向拉伸試驗、成型極限試驗以及擴孔試驗研究了寶鋼1 500 MPa超高強鋼的成形特性，證明該材料具有優異的整體成型性能。朱曉東等[7]以1 500 MPa級別的冷軋馬氏體鋼為研究對象,測試了其90°彎曲性能和在不同溫度的韌性及斷裂方式，發現當彎曲半徑/板厚達到2.5時，1 500 MPa的馬氏體鋼板可以滿足90°彎曲成形要求，并且在-40 ℃以上有穩定的沖擊韌性值。侯登義等[8]從淬火溫度、保溫時間、化學成分、冷卻速度等角度改善了1 500 MPa級超高強度耐磨鋼板淬透性不足的問題。盡管上述學者們針對1 500 MPa超高強鋼材料已經進行了一些性能檢測，但是對于1 500 MPa冷軋馬氏體鋼在冷彎成型、沖壓領域常用的彎曲回彈性能還沒進行系統性研究，對影響其彎曲回彈性能的相關因素還需進一步研究。

韓非等[9-10]基于三點彎曲試驗，研究了1 180 MPa級別的超高強馬氏體鋼的彎曲性能，以最小彎曲半徑表征材料的彎曲成型性能，發現隨著強度升高，斷后伸長率接近性下降；相對彎曲半徑值增大，彎曲性能下降，但并無良好的線性關系。葛德龍等[11]人對1 000 MPa級別超高強度馬氏體鋼板進行了三點彎曲試驗，發現相對彎曲半徑與彎曲角度成正比，與經典塑性理論不同，彎曲角度與材料延伸率無關。S.K.Panthi[12]研究了材料參數對回彈的影響，指出隨著材料屈服強度的增大，回彈量增加；隨著彈性模量的增大，回彈量減小。國內外學者都對1 300 MPa級別以下超高強鋼進行了彎曲回彈性能的相關研究，但是隨著1 500 MPa馬氏體鋼材料在冷彎成型工藝中的應用日益增加，有關1 500 MPa級馬氏體鋼材料的彎曲回彈性能研究已經非常必要。

為研究其彎曲回彈性能，本文將基于1 300 MPa級以下的彎曲回彈性能研究方法，采用三點彎曲試驗，從影響傳統材料彎曲性能的壓下速度、相對彎曲半徑、材料板厚、彎曲半徑4個主要因素對1 500 MPa超高強鋼進行試驗分析。

1 三點彎曲試驗

1.1 試驗方法

本文基于三點彎曲試驗研究1 500 MPa超高強鋼的彎曲回彈性能。通過改變沖頭壓下速度、厚度、彎曲半徑等參數，測量并記錄樣件的彎曲角度和回彈角度。試驗在SHT4605微機控制電液伺服萬能試驗機上進行，支撐輥輥間距計算公式為

D輥心距=D輥輪+2R沖頭+3d料厚。

試驗材料選用1 500 MPa冷軋酸洗裸板。由電火花切割為60 mm×50 mm的薄片試樣(沿寬度方向60 mm，沿軋制方向50 mm)，如圖1所示。試驗時沖頭可更換，安裝在凸模固定座上固定于試驗機頂部，截面方向根據定位銷定位，軋制方向根據預設標記定位。

圖1 料片放置示意圖Fig.1 Schematic diagram of test sheet placement

1.2 角度的測量

彎曲角度的測量是三點彎曲試驗的難點，在線測量彎曲角度過程繁復，誤差較大，無法獲得準確的彎曲角度數據。有限元仿真軟件可以模擬三點彎曲試驗的彎曲和回彈全部過程，為了排除有限元法對回彈計算的誤差，本文使用MSC.Marc軟件模擬三點彎曲試驗的彎曲過程，應用幾何原理在軟件中測量一定參數下的彎曲角度，采用量角器測量試驗后的樣件得到回彈后角度。其中，為與輥壓設計中角度保持一致，定義彎曲角、回彈后角度如圖2所示，用θ1表示彎曲角度，θ2表示回彈后角度。回彈角度與實際工況、材料性能密切相關，試驗時材料彎曲到指定狀態后卸載外力，量角器測量實際回彈后角度。

圖2 彎曲回彈角度定義Fig.2 Definition of bending rebound angle

2 結果與討論

2.1 回彈影響因素分析

2.1.1沖頭壓下速度對彎曲回彈性能的影響

通過改變沖頭壓下速度，觀察材料回彈角度變化趨勢。試驗鋼為1 500 MPa馬氏體鋼，板厚為1.0 mm，彎曲半徑為R5，壓下行程為15 mm，速度分別為5 mm/min、10 mm/min、15 mm/min、20 mm/min，試驗數據如表1所示。

表1數據表明，行程為15 mm，隨著壓下速度的改變，回彈角度稍有變化，但整體變化在2°之內，彎曲角度為113°不變。但是，當沖頭壓下速度在20 mm/min時回彈角度沒有波動，最穩定。本文其他影響因素的試驗速度都采用20 mm/min。

表1 不同壓下速度彎曲回彈角度對比Tab.1 Comparison of bending rebound angles with different reduction speeds

2.1.2 相對彎曲半徑對回彈角度的影響

研究者對比折彎成型和輥彎成型的角度，發現輥彎成型回彈角度明顯小于折彎的回彈角度。Biswas[13]基于彎折理論及其試驗，加入對材料特性參數的考慮，在前人的基礎上提出了Biswas回彈計算公式。本節將在彎曲半徑分別為R5、R6、R8，厚度分別為1.0 mm、1.2 mm、1.6 mm，相對彎曲半徑為5的工況下進行三組試驗。

對Biswas回彈計算公式進行簡化[14-15]得到

(1)

式中，ri1為彎曲半徑，ri2為回彈后半徑，t為板材厚度，θ1為彎曲角度，Δθ為回彈角度，A、B、C、D為材料楊氏模量、板料厚度和屈服應力經數學推導所得系數。由式(1)可以看出回彈角度只與相對彎曲半徑相關。等相對彎曲半徑狀態下，回彈角度應相等。

三點彎曲試驗中，由于每種材料的彎曲回彈性能不同，試驗中彎曲角度、回彈角度難以控制。為使不同試驗數據有對比性，具有相同的因變量，試驗中以沖頭下壓行程為因變量，收集同一行程下材料的回彈量。然后將離散有限的試驗數據點進行數值分析，采用一種能表征該區間內數據變化規律的數學模型進行擬合，以獲取描述整體變化趨勢的相關公式，便于對比分析。根據數據擬合程度，最終選用了擬合程度高且便于計算的三次多項式數學模型。

圖3為等相對彎曲半徑試驗數據擬合曲線，R8/1.6、R5/1.0和R6/1.2三條擬合曲線對應相關系數算得分別為99.75%、99.74%和99.32%，均在99%以上，表明三次多項式曲線與試驗數據擬合良好。由圖可知，[0,50]區間，R6/1.2與R5/1.0曲線基本重合，R8/1.6曲線位于兩條曲線上方回彈最小；[50,100]區間，R6/1.2曲線處于中間位置，但走勢變換明顯；在[100,160]區間內，R6/1.2曲線位于最上方，但與R8/1.6曲線延長線基本重合。三條曲線未見重合且整體變化無明顯規律。

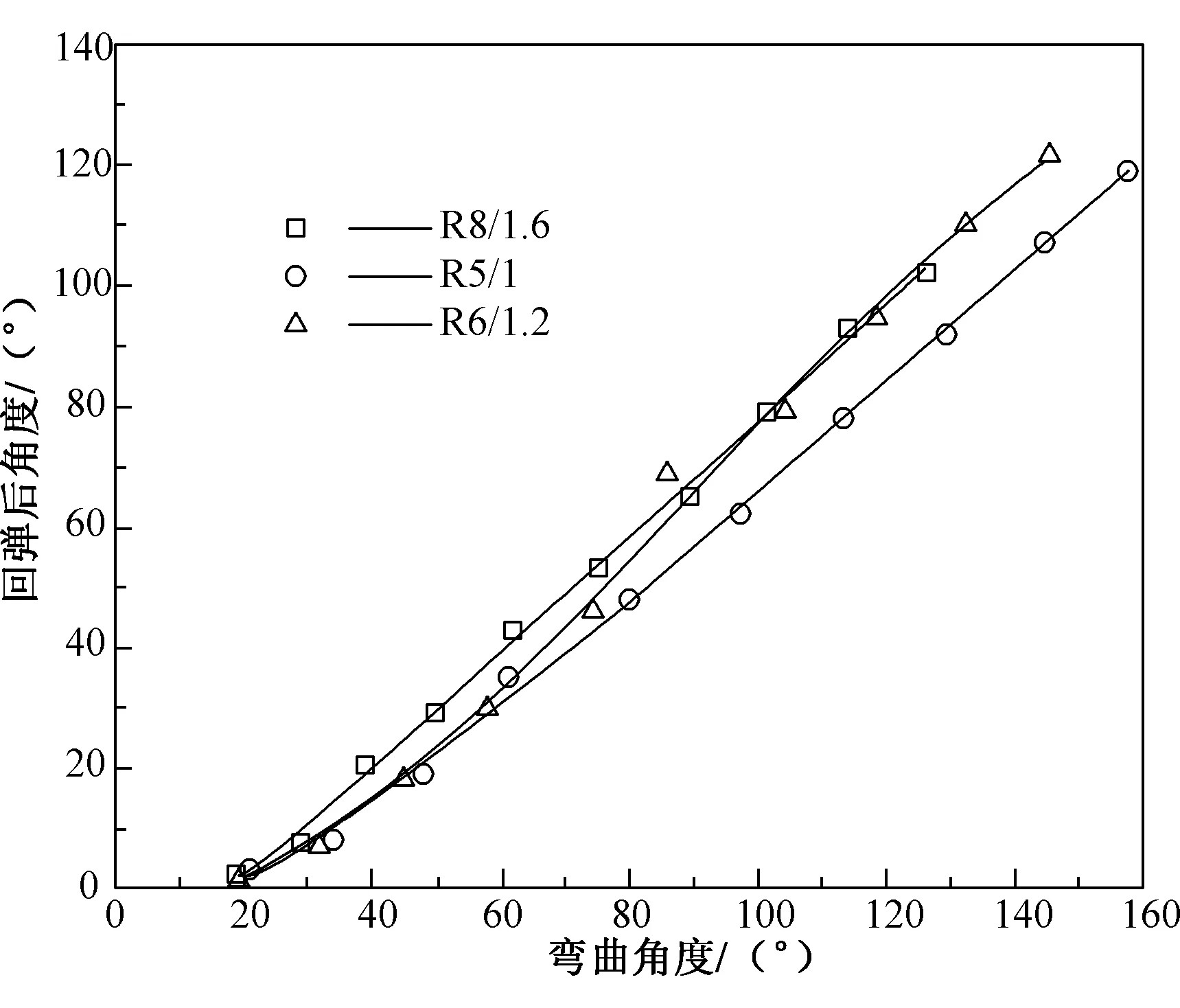
圖3 等相對彎曲半徑彎曲回彈曲線Fig.3 Bending rebound curve with equal relative bending radius

從上述曲線可以看出，當相對彎曲半徑相同的情況下，相同的彎曲角度對應的回彈角度并不相同。故該Biswas回彈計算公式無法用來準確計算1 500 MPa級超高強鋼彎曲回彈量。因此，本文提出1 500 MPa級別的超高強鋼回彈角度的計算，通過對試驗數據回歸分析的方法擬合計算公式進行彎曲回彈性能的表征。

2.1.3 厚度對彎曲回彈性能的影響

本文選用1 500 MPa馬氏體鋼進行試驗，測得三種厚度板材力學性能數據如表2所示，表中數據說明不同厚度的材料其力學性能大致相同。本節在材料力學性能一致的基礎上對不同板厚的彎曲回彈性能進行了對比試驗。

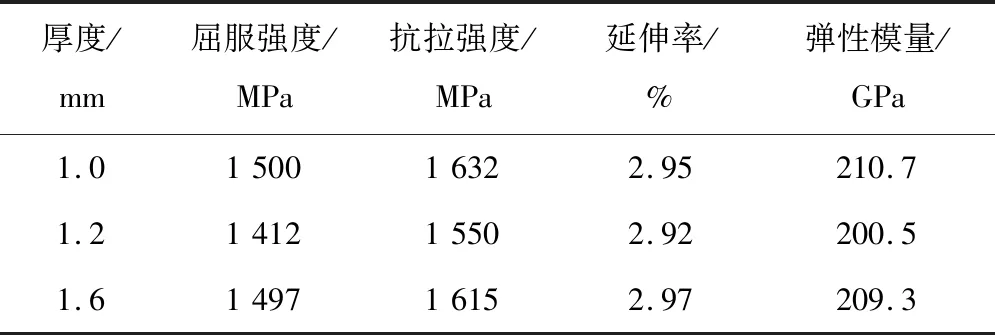
表2 不同厚度材料力學性能對比Tab.2 Comparison of mechanical properties of materials with different thickness

在相同工況下對不同厚度的材料進行試驗，彎曲半徑為R5，壓下行程為3～21 mm，間隔2 mm，板厚分別為1.0 mm、1.2 mm和1.6 mm。表3為部分試驗數據，應用線性回歸原理擬合得到對應的彎曲回彈曲線如圖4所示，板厚1.0 mm、1.2 mm和1.6 mm三條擬合曲線對應相關系數算得分別為99.84%、99.82%和99.89%，三條擬合曲線相關系數均達到99.8%，表明三次多項式曲線與試驗數據擬合良好，可以采用該三次多項式計算彎曲和回彈角度。

表3 不同厚度彎曲回彈角度對比Tab.3 Comparison of bending rebound angles of different thicknesses

圖4 不同厚度鋼材彎曲回彈曲線Fig.4 Bending rebound curve of steel with different thickness

觀察曲線[0,50]區間，1.2 mm曲線與1.0 mm曲線基本重合，1.6 mm曲線位于兩條曲線上方回彈最小；[50,140]區間，1.2 mm曲線處于中間位置，同 樣的彎曲角度下，1.6 mm厚材料回彈后角度最大，1.0 mm材料回彈后角度最小；[140,180]區間1.2 mm與1.6 mm曲線基本重合，1.0 mm曲線位于最下方回彈最大。

由試驗數據經過三次多項式擬合得到不同板厚下的彎曲回彈角度計算公式。

厚度1.0 mm材料的彎曲回彈公式為

(2)

厚度1.2 mm材料的彎曲回彈公式為

(3)

厚度1.6 mm材料的彎曲回彈公式為

(4)

式中，θ1為彎曲角度，θ2為回彈后角度。

在冷彎成型工藝和冷沖壓工藝中90°是比較常用的彎曲角度，將彎曲角度θ1=90°分別代入式(2)～(4)中，計算回彈角度如表4所示。彎曲角度為90°，當厚度由1.0 mm增加到1.6 mm時，同樣彎曲90°，材料回彈由38°減小到20°，回彈減少了18°。同樣的彎曲角度下，隨著板厚的增加，回彈后角度增大，回彈減小。

表4 不同厚度計算結果對比Tab.4 Comparison of calculation results of different thicknesses

2.1.4 彎曲半徑對回彈角度的影響

在相同工況下改變彎曲半徑，對比鋼材的彎曲回彈性能，板厚為1.0 mm，壓下行程為3～21 mm間隔2 mm，支撐輥輥間距分別為43 mm、49 mm和53 mm，彎曲半徑為R5、R8和R10，三種不同彎曲半徑下的彎曲回彈曲線如圖5所示，R5、R8和R10三條擬合曲線相關系數分別為99.84%、99.65和99.73%，均在99.6%以上，擬合曲線與試驗數據重合性良好，可以采用該三次多項式計算彎曲和回彈角度。觀察可得，三條曲線距離較近，彎曲半徑改變對回彈角度的影響不明顯。在[0，50]與[140，180]區間內，三條曲線基本重合；[50，140]區間內，R5曲線位于最上方，R10位于最下方，此時R5回彈最小，R10回彈最大。

圖5 不同彎曲半徑鋼材彎曲回彈曲線Fig.5 Bending rebound curve of steel with different bending radius

由試驗數據經過三次多項式擬合得到不同彎曲半徑下的彎曲回彈角度計算公式如下：

材料在R5彎曲半徑下的彎曲回彈公式為

(5)

材料在R8彎曲半徑下的彎曲回彈公式為

(6)

材料在R10彎曲半徑下的彎曲回彈公式為

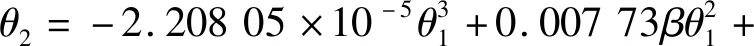
(7)

將θ1=90°代入式(5)～(7)中，得出對應的回彈角度，如表5所示。彎曲角度為90°，彎曲半徑由R5增加到R8，材料回彈由31°增加到38°，回彈增加了7°。同樣的彎曲角度下，彎曲半徑增大，回彈后角度減小，回彈增加。

表5 不同彎曲半徑計算結果對比Tab.5 Comparison of calculation results of different bending radius

2.2 各影響因素對彎曲回彈性能的對比分析

2.1節中分析了各因素對板材回彈的影響，壓下速度和相對彎曲半徑對1 500 MPa馬氏體鋼的彎曲回彈性能無明顯影響。但是，厚度、彎曲半徑對材料的彎曲回彈性能有明顯的作用規律，當彎曲半徑為R5時板厚影響回彈數據對比如表6所示，當板厚為1.0 mm時彎曲半徑影響數據對比如表7所示。彎曲角度為90°，材料增厚，回彈變化大于8°；彎曲半徑增加，回彈變化在4°以內。分別計算回彈相對于板厚和彎曲半徑變化的百分比，如表8所示。可得：彎曲角度為90°，板厚改變20%，回彈角度改變了19%；板厚改變40%，回彈角度改變了33%；板厚改變60%，回彈角度改變了46%。彎曲半徑改變25%，回彈角度改變12%；彎曲半徑改變60%，回彈角度改變10%；彎曲半徑改變100%，回彈角度改變23%。經對比，在影響彎曲回彈的影響因素中，板厚與彎曲半徑同樣變化60%的前提下，材料的彎曲回彈改變比例相差36%。因此，對于1 500 MPa馬氏體超高強鋼材料而言，材板厚度是影響其彎曲回彈性能的最關鍵因素，工藝設計時需著重考慮。

表6 板厚影響回彈數據對比Tab.6 Comparison of material thickness influence springback data

表7 彎曲半徑影響回彈數據對比Tab.7 Comparison of bending radius influence springback data

表8 影響因素比重分析Tab.8 Analysis of the proportion of influencing factors

3 結論

本文通過三點彎曲試驗測量1 500 MPa超高強鋼在壓下速度、材料板厚、彎曲半徑、相對彎曲半徑等影響因素下的彎曲回彈性能，得到的結論如下：

1)當壓下速度在5～20 mm/min變化時，隨著壓下速度的改變，回彈角度稍有變化，但整體變化在2°之內。但是，當沖頭壓下速度在20 mm/min時回彈后角度沒有波動，最穩定。

2)對于1 500 MPa超高強馬氏體鋼而言，相對彎曲半徑相等的情況下，回彈性能并不一致，且等相對彎曲半徑下回彈角度無規律性變化。同樣的彎曲角度下，隨著材料的增厚，回彈減小。同樣的彎曲角度下，彎曲半徑增大，回彈增加。

3)材料板厚和彎曲半徑對材料的彎曲回彈性能影響顯著，其余因素無明顯影響。板厚與彎曲半徑同樣變化60%的前提下，材料的彎曲回彈改變比例相差36%。因此，對于1 500 MPa馬氏體超高強鋼材料而言，材料板厚是影響其彎曲回彈性能的最關鍵因素，在冷彎成型設計中應著重考慮材料板厚。