硅基Ⅳ族SiGeSn三元合金晶格結構、電子結構和光學性質的第一性原理
孫生柳,黃文奇,張立鑫,諶珍雨,王 浩
(1.北京信息科技大學,北京材料基因工程高精尖創新中心,北京 100101;2.北京信息科技大學理學院,北京 100101)
0 引 言
由于信息技術的發展對數據處理速度與精度要求的提高,傳統的集成電路面臨著功耗上升、成本高和電磁干擾等一系列問題,摩爾定律越來越難維持,芯片發展逐漸變緩[1]。而硅基光互連技術[2-4]的提出,使得集成電路的發展有望突破此瓶頸。硅基Ⅳ族材料(如GeSn、GePb等)由于可與互補金屬氧化物半導體(CMOS)工藝兼容[5],已成為該領域的熱點。2015年,Wirths等[6]在Si上生長出具有直接帶隙的GeSn合金,并實現了GeSn合金光致激射發光,這一研究成果為制備出與CMOS工藝兼容的硅基光電子集成技術開辟了新途徑。目前,硅基光互連芯片上所需要的大部分光學器件已被研制出來,如光探測器、光波導、光調制器等[3,7],但基于電致激射的GeSn高效光源問題依然懸而未決。這是因為對GeSn的研究仍然存在一系列問題,例如高質量的材料生長、高濃度的原位摻雜、合理的應變引入等[8]。其中在材料生長過程中,GeSn合金與Ge或Si襯底之間存在較大的晶格失配,會嚴重影響其生長質量[9-12]。其次,GeSn會受到Ge或Si襯底的壓應變作用,導致其能帶結構轉向間接帶隙[13-15],不利于其發光效率的提高。
而SiGeSn三元合金由于具有更大的晶格常數調控范圍,使用其作為緩沖層可以解決GeSn晶格失配和壓應變帶來的問題[16-18]。Peng等[19]在硅基上生長的GeSn中引入Si元素,通過調節Si的組分可以獲得晶格匹配的GeSn/SiGeSn量子阱結構,且高質量的SiGeSn緩沖層還使得GeSn處于無應變或者張應變的狀態,實驗中觀測到非常明顯的室溫發光現象。但目前,由于實驗成本昂貴,對于SiGeSn的晶格常數研究還不夠全面,其作為緩沖層所需的組分比例難以精確確定。
此外,SiGeSn三元合金由于具有更大的帶隙調控范圍,可以應用于更寬的波段范圍。GeSn合金帶隙的調控范圍在0~0.8 eV之間,只能應用于紅外波段[20]。而SiGeSn合金由于Si的引入,其帶隙調控范圍擴大至1.4 eV[21]。但目前對于SiGeSn帶隙調控的微觀物理機制研究還未見報道。
除實驗研究外,理論計算可以預測材料的基本性質,為實驗研究提供理論指導。Moontragoon等[22-23]采用經驗贗勢理論研究了SiGeSn合金的能帶結構,得到了帶隙分布規律。但他們采用的模型基于虛擬晶體近似,不能反映各種原子之間的相互作用。Zhao等[24]采用基于密度泛函理論的第一性原理方法對五個組分的SiGeSn模型進行結構優化,并采用屏蔽交換局域密度近似計算了它們的電子結構性質。但他們所研究的樣本較少,所采取的合金模型未能體現元素分布的隨機性,因此不能全面反映SiGeSn晶格結構和電子結構性質的變化規律。
為解決以上研究存在的問題,本文將利用基于密度泛函理論(DFT)的第一性原理方法研究Si1-x-yGexSny在不同組分(x∈(0~1.0)和y∈(0~0.2))下的晶格常數、能帶結構、態密度和光學性質。計算中采用準隨機近似(SQS)方法模擬各種原子的隨機分布,并使用雜化泛函修正能帶間隙,以期更加全面和精確地理解其性質的物理機制,掌握這些性質隨組分的變化規律,為其實驗和應用研究提供理論指導。
1 計算模型與方法
本研究采用的是基于DFT的第一性原理方法,該方法被廣泛用于Ⅳ族多元合金以及其他材料的理論計算[25-31]。由于Sn元素在Si和Ge晶體中容易偏析和分凝,其組分一般較低[32-33]。因此在本文中,Ge組分設定為x∈(0~1.0),Sn組分設定為y∈(0~0.2)。為了描述合金中各種元素分布的隨機性,本研究采用Walle等[34]提出的SQS方法,生成包含64個原子的超胞模型。
本文的計算包括晶格結構優化、電子結構和光學性質計算,均由PWmat軟件程序包[35]實現。計算中使用雜化泛函(HSE)并結合局域密度近似(LDA)描述電子的交換關聯能,采用模守恒贗勢(NCPP)分別對內層電子態進行贗化。經收斂性測試,計算中的所有截斷能設為816.342 eV,并采用MonkhorstePack方案對布里淵區進行2×2×2網格k點采樣。在晶格優化中,力收斂設定為0.3 eV/nm。
(1)
2 結果與討論
2.1 晶格結構
首先研究了Si1-x-yGexSny隨Ge和Sn濃度變化時,其晶格常數的變化規律。對于不同組分的Si1-x-yGexSny合金,通過改變Ge原子與Sn原子的數目來模擬。圖1為使用SQS方法產生的Si0.906 25Ge0.046 875Sn0.046 875的合金模型。為驗證研究方法的可靠性,將現有的實驗數據與計算結果進行比較,其結果如表1所示。對于Si、Ge和Sn,計算所得晶格常數分別為0.544 434 nm、0.557 22 nm和0.644 25 nm,與對于實驗值[37]0.543 10 nm、0.565 79 nm、0.648 92 nm的相對誤差分別是0.245 62%、1.514 20%和0.719 66%。對于二元合金,分別計算了Si1-xGex、Si1-xSnx、Ge1-xSnx隨組分變化時的晶格常數,并計算了它們的彎曲系數。其中,Si1-xGex、Si1-xSnx和Ge1-xSnx彎曲系數分別為bSiGe=-0.002 017 nm、bSiSn=0.042 26 nm和bGeSn=0.021 935 nm,結果表明二元合金晶格常數均偏離Vegard定律,且與已有實驗數據bSiGe=-0.002 66 nm[38]、bGeSn=0.021 1 nm[39]非常吻合。因此,本文所采用的計算方法具有很高的精度。

圖1 SQS方法產生的Si0.906 25Ge0.046 875Sn0.046 875合金模型Fig.1 Si0.906 25Ge0.046 875Sn0.046 875 alloy model produced by the SQS method

表1 Si、Ge、Sn、Si1-xGex、Si1-xSnx以及Ge1-xSnx的晶格常數及其彎曲系數Table 1 Lattice constants and bowing factors of Si,Ge,Sn,Si1-xGex,Si1-xSnx and Ge1-xSnx
對于三元合金,Sn濃度y固定時,Si1-x-yGe(x=0.093 75~0.796 875)Sny的彎曲系數b隨著Ge濃度x增加分別為:b1=-0.012 23 nm,b2=-0.035 58 nm,b3=-0.051 67 nm,b4=-0.060 52 nm,b5=-0.062 11 nm,b6=-0.056 44 nm,b7=-0.043 53 nm和b8=-0.025 7 nm,如圖2(a)所示。可以看出:當Ge濃度x在0.093 75~0.5之間時,b1~b5的值是逐漸減小的;而當Ge濃度x從0.5增加到0.796 875時,b6~b8的值逐漸增大。這是由于合金材料中不同元素之間的電負性差值ΔE變化[18]。為了深入理解這種現象產生的原因,定義ΔE為SiGeSn合金不同元素之間電負性差值的總和述:
(2)
式中:ΔE1、ΔE2、ΔE3分別為Si1-x-yGexSny中Si和Ge、Ge和Sn以及Si和Sn之間的電負性差值,P為元素的修正鮑林電負性值,其中Si為1.90,Ge為2.01,Sn為1.96。圖2中的(b)和(c)分別為Si0.906 25-xGe(x=0.093 75~0.796 875)Sn0.093 75的電負性差值ΔE和彎曲系數b在不同Ge濃度下的變化趨勢對比圖。由圖可知,彎曲系數b與合金不同元素之間的電負性差值ΔE變化趨勢基本一致。
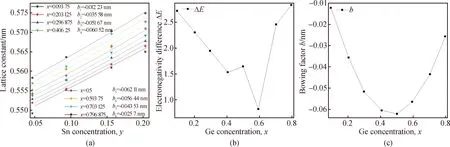
圖2 (a)Si1-x-yGexSny晶格常數隨著Sn濃度y遞增的變化趨勢;(b)電負性差值ΔE隨Ge濃度x增加的變化趨勢;(c)彎曲系數b隨Ge濃度x增加的變化趨勢Fig.2 (a)Change trend of the lattice constant of Si1-x-yGexSny with increasing Sn concentration y;(b)electronegativity difference ΔE changes with the increase of Ge concentration x;(c)bowing factor b changes with the increase of Ge concentration x
由于實驗中需要準確確定Si1-x-yGexSny在不同組分下的晶格常數,給出了它的計算公式:
a=-3.626x2y2+1.006x2y+3.422x2+0.007xy2-0.183xy-0.789x+0.099y2+1.006y+5.453
(3)
由公式(3)可以確定Si1-x-yGexSny的晶格常數,為其作為緩沖層所需組分比例的確定提供理論指導。例如,對于GeSn合金的晶格失配問題,蘇少堅等[40]通過實驗表明對于生長在Ge緩沖層上的GeSn合金,當晶格失配度小于1%時,GeSn材料的質量較好。而當晶格失配度大于1%時,質量稍差。如果將GeSn合金生長在Si1-x-yGexSny緩沖層上,可以有效降低GeSn的晶格失配度。圖3黑色實線部分標出了當具有準直接帶隙的Ge0.915Sn0.085生長在Si1-x-yGexSny緩沖層上時,晶格失配度小于1%的Si1-x-yGexSny的組分范圍。對于GeSn合金受到Ge襯底壓應變的問題,文獻[18]指出Si1-x-yGexSny可以為(100)晶向GeSn提供張應變,這更利于GeSn合金的發光。圖3紅線部分標出了可為準直接帶隙Ge0.915Sn0.085合金提供張應變的Si1-x-yGexSny的組分范圍。

圖3 三元合金Si1-x-yGexSny晶格常數隨著Ge和Sn濃度遞增的變化趨勢Fig.3 Change trend of the lattice constant of the ternary alloy Si1-x-yGexSny with the increasing concentration of Ge and Sn
2.2 電子結構
為了研究Si的引入對SiGeSn合金電子結構的影響,分別計算Ge0.906 25Sn0.093 75和Si0.062 5Ge0.843 75Sn0.093 75的沿布里淵區高對稱路徑:L點(0.5,0.5,0.5)至Г點(0,0,0)、Г點(0,0,0)至X點(0.5,0,0.5)的能帶結構[15],導帶的三個能量最小值分別出現在L谷(0.5,0.5,0.5)、Г谷(0,0,0)和X谷(0.5,0,0.5)附近,分別用EL、EГ和EX表示,結果如圖4所示。從圖中可以看出,Ge0.906 25Sn0.093 75的導帶底和價帶頂都處于Г點,為直接帶隙結構,其帶隙值為0.280 58 eV,這與實驗結論[6]非常吻合。而對于相同的Sn濃度,Si0.062 5Ge0.843 75Sn0.093 75也呈現出直接帶隙特征,其帶隙值為0.364 04 eV。這說明Si的引入不僅可以提高合金的帶隙,還保持了直接帶隙的特征。因此,在拓寬硅基高效光源的發光波段,SiGeSn相較于GeSn合金具有更大的優勢。

圖4 相同Sn濃度下,(a)Ge0.906 25Sn0.093 75和(b)Si0.062 5Ge0.843 75Sn0.093 75的能帶結構Fig.4 Energy band structures of (a)Ge0.906 25Sn0.093 75 and (b)Si0.062 5Ge0.843 75Sn0.093 75 for the same Sn concentration
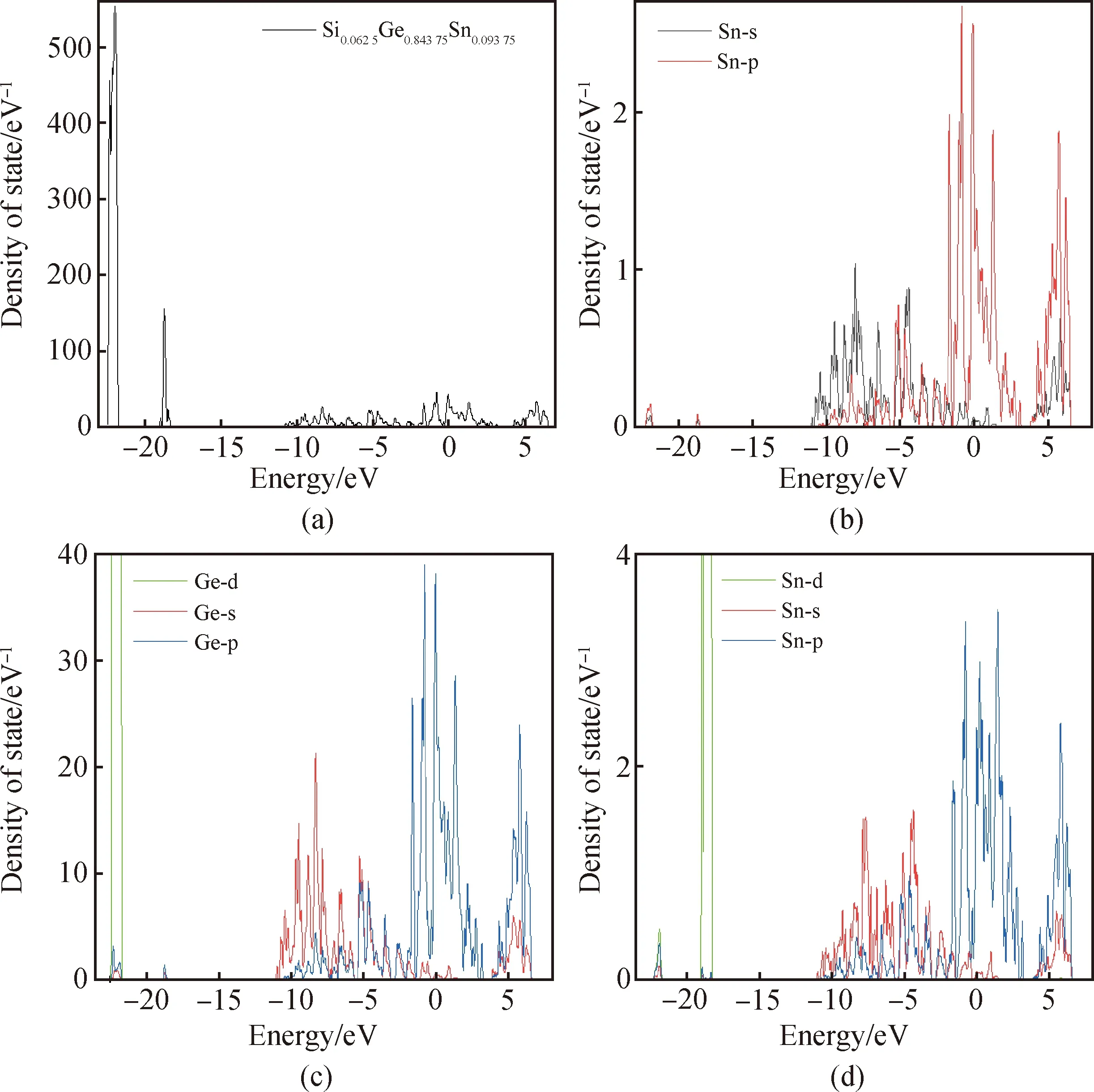
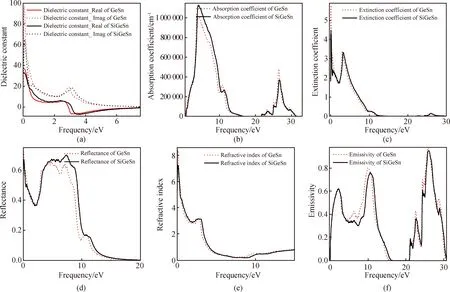
為了進一步研究Si對于合金能帶結構的影響機理,計算并比較Ge0.906 25Sn0.093 75和Si0.062 5Ge0.843 75Sn0.093 75合金的總態密度和部分態密度,如圖5和圖6所示。可以看出在整個價帶區域,它們的態密度分布非常相似:在價帶的低能量部分(-25 eV 圖5 Ge0.906 25Sn0.093 75的總態密度(a),部分態密度(Sn(b)和Ge(c))Fig.5 Total density of states (a),partial density of states Sn(b)and Ge(c)for Ge0.906 25Sn0.093 75 圖6 Si0.062 5Ge0.843 75Sn0.093 75的總態密度(a),部分態密度(Sn(b)、Ge(c)和Si(d))Fig.6 Total density of states (a),partial density of states Sn(b),Ge(c)and Si(d)for Si0.062 5Ge0.843 75Sn0.093 75 為了研究Si的引入對SiGeSn合金光學性質的影響,分別計算相同Sn濃度的Ge0.906 25Sn0.093 75和Si0.062 5Ge0.843 75Sn0.093 75的介電函數譜、吸收系數、消光系數、反射率、折射率和發射率,如圖7所示。對于介電函數虛部,Ge0.906 25Sn0.093 75的峰值主要出現在0.70 eV和3.56 eV。而Si0.062 5Ge0.843 75Sn0.093 75的峰值由于Si的引入則呈現明顯的藍移,主要出現在0.80 eV和3.86 eV,且其值整體均小于Ge0.906 25Sn0.093 75。對于介電函數實部,Si0.062 5Ge0.843 75Sn0.093 75的靜介電常數ε(0)為33.18,略小于Ge0.906 25Sn0.093 75的37.24。對于吸收系數,Si0.062 5Ge0.843 75Sn0.093 75的最高吸收峰出現在更低的波長范圍,在0 eV至20 eV內Si0.062 5Ge0.843 75Sn0.093 75的值高于Ge0.906 25Sn0.093 75,而在20 eV至33 eV內則相反。對于消光系數,Si0.062 5Ge0.843 75Sn0.093 75和Ge0.906 25Sn0.093 75的最高峰值均出現在0.8 eV附近,Ge0.906 25Sn0.093 75的值略高。對于反射率,在0 eV至3.4 eV內Si0.062 5Ge0.843 75Sn0.093 75的值大部分略低于Ge0.906 25Sn0.093 75,而在3.4 eV至20 eV內則相反。在低頻范圍,Si0.062 5Ge0.843 75Sn0.093 75的折射率略高于Ge0.906 25Sn0.093 75,而在高頻范圍時它們都迅速衰減。對于輻射率,Si0.062 5Ge0.843 75Sn0.093 75的值在整個頻段都略低于Ge0.906 25Sn0.093 75。 圖7 Ge0.906 25Sn0.093 75和Si0.062 5Ge0.843 75Sn0.093 75的介電函數(a)、吸收系數(b)、消光系數(c)、反射率(d)、折射率(e)和發射率(f)Fig.7 Dielectric function (a),absorption coefficient (b),extinction coefficient (c),reflectivity (d),refractive index (e)and emissivity (f)of Ge0.906 25Sn0.093 75 and Si0.062 5Ge0.843 75Sn0.093 75 以上分析表明由于Si的引入,SiGeSn較GeSn具有更寬的光吸收波長范圍,其他光電性質也呈現出不同的分布。因此,相比于GeSn,SiGeSn光電探測器在全通信頻段的硅基光通信中具有更大的應用潛力。 本文利用基于密度泛函理論的第一性原理方法,研究Si1-x-yGexSny在不同組分(x∈(0~1.0)和y∈(0~0.2))下的晶格常數、能帶結構、態密度和光學性質。計算中采用準隨機近似方法模擬各種原子的隨機分布,并使用雜化泛函修正能帶間隙。首先,計算了Si、Ge、Sn和二元合金(Si1-xGex、Si1-xSnx、Ge1-xSnx)的晶格常數,并與實驗值進行比較。結果表明二元合金晶格常數均偏離Vegard定律,其彎曲系數與實驗數據和他人計算結果吻合。其次,計算了Si1-x-yGexSny在不同組分(x∈(0~1.0)和y∈(0~0.2))晶格常數,發現三元合金的彎曲系數先減小后增大,這主要是由合金電負性差值的變化造成的。給出了Si1-x-yGexSny晶格常數的理論計算公式,并為GeSn合金生長的晶格失配和壓應變問題提供了解決方案。第三,計算了Si0.062 5Ge0.843 75Sn0.093 75和Ge0.906 25Sn0.093 75的能帶結構,結果表明它們均呈現直接帶隙特征,且三元合金的帶隙值大于二元合金的帶隙值。總態密度和部分態密度的計算結果表明,Si-p電子態的貢獻是造成合金帶隙變化的最主要原因。第四,計算和比較了Si0.062 5Ge0.843 75Sn0.093 75和Ge0.906 25Sn0.093 75的介電函數譜、吸收系數、消光系數、反射率、折射率和發射率等光學性質。這些結果均表明,Si的引入不僅可以提高SiGeSn合金的帶隙,還使其保持了直接帶隙的特征,SiGeSn的光學性質較GeSn呈現不同的相應波段范圍。因此,在拓寬硅基高效光源的發光波段方面,SiGeSn相較于GeSn合金具有更大的優勢。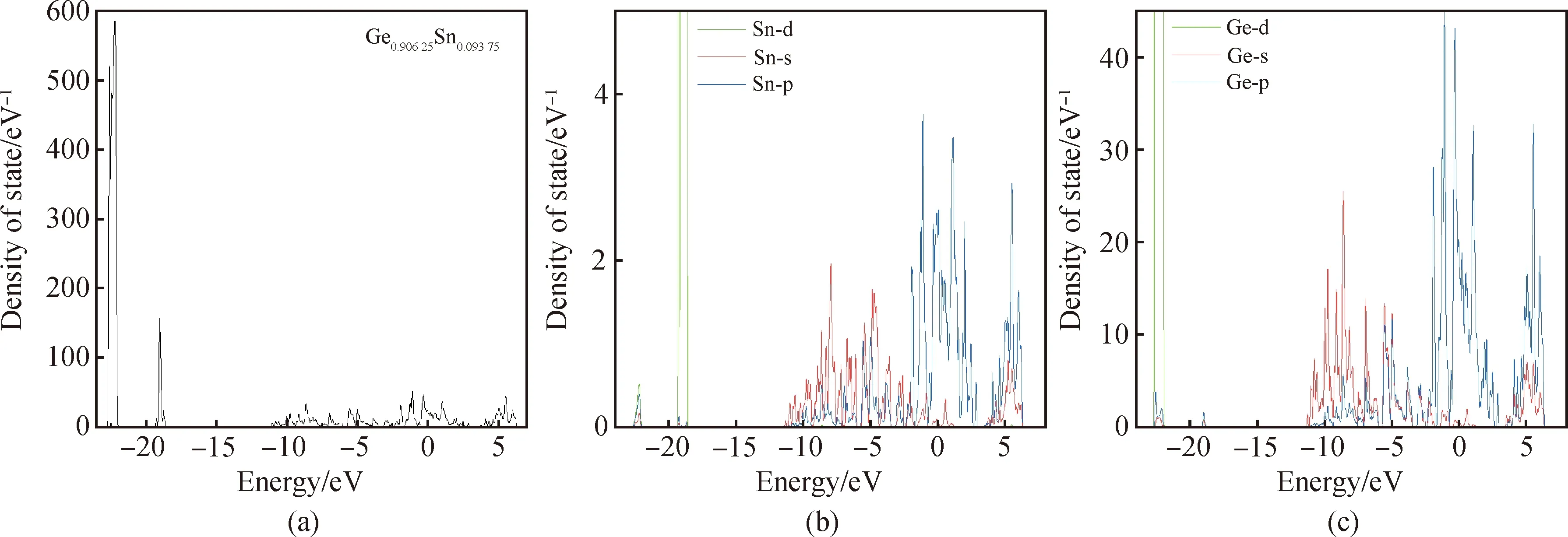
2.3 光學性質
3 結 論

