曲邊平面磚的點陣原理與工程設計

李效東

（國防科技大學 文理學院，湖南 長沙410073）

長久以來，人們常用一種正規形狀（如四方形、矩形、正六邊形等）的平面磚無間隙、無重疊地鋪設地面或墻面等任意面積的平面F。但是在建筑技術（地磚、墻磚、大型穹頂、互鎖磚等）、平面裝飾藝術（紡織品、墻紙等）、實用技術（拼接家具木板和地板等）和眾多工業領域均希望有多種非正規形狀的多邊形甚至曲線邊緣的平面磚型可供選擇。這樣不僅可以產生各種不同風格的視覺效果，也可能因為磚間的接觸線和接觸角的改變而優化工程施工技術和實用性能。此外，平面磚的幾何規律和對稱性在科學研究中具有重要意義，如可以幫助理解晶體的晶面結構[1-2]以及外延薄膜、分子自組裝等現象。

平面磚藝術的產生可追溯到人類的早期文明[3-4]。人們早已發現，有些非規則形狀的平面磚可以拼合鋪排成如圖1-b，c 所示的圖案。多年以來，人們不斷地發現了許多不同形狀的，周期性和非周期性的平面磚型，有的還詳細描述了具體多邊形平面磚的幾何參數。Grünbaum 的專著[5]以巨大的文獻量概括了多年來在此領域的研究積累。盡管平面磚的復雜性給系統化描述帶來一定的分歧，但仍可進行大致的分類。圖2 歸納了不同類型的多邊形及其拼合方式。為什么一種看起來本身似乎不具備任何對稱性的多邊形[6-7]，甚至曲線邊緣的平面能夠“湊巧”成為平面磚？怎樣按照一定的規則設計出不同類型和風格的平面磚？本文的研究目的是探索這些問題的答案。

圖1 平面磚及其鋪排實例

1 定義

本文提出一類全部邊緣可為任意曲線的點陣型平面單磚T，其可以無間隙，無重疊，周期性地鋪排成無限大平面F。為了明確概念，本文將曲邊T 的討論范圍作以下規定。（1）周期性（periodic），排除圖2-a 中的螺旋性[8]，因其不可用平面點陣表示，且鋪設平面受限；（2）單形（monohedral），排除圖2-b 中的復形，或多種磚形混拼；（3）單面（isohedral），排除圖2-c 中的手性雙面磚。因地磚、墻磚的正反兩面材質不同，手性對映體實際上屬于特殊的雙形。（4）相鄰磚線段全接觸（normal），此為曲邊嚙合的幾何要求，故排除圖2-d，e 中的線段的非全接觸，盡管很多復形和手性對映體也能形成曲邊磚，但暫不在此討論。本文僅限于圖2-f 中單形、單面的T。

圖2 不同類型的多邊形平面磚

無論T 的曲邊形狀如何復雜，均能以某種凸角多邊形（convex polygon）作為基形，在保持基形面積不變的前提下，其直線邊按照一定規律曲線化。為數眾多的多邊形固然可以鋪滿F，但只有滿足一定幾何要求的多邊形才可以全曲線化而成為T 的基形。

按此定義的邊緣可全曲線化的平面磚T 分為“基礎平面磚”TE、三種“多重平面磚”TN、TNX和TNX/2。其中TE可以順著平面上的兩個特定方向（或軸）周期性地平移鋪排，構成無間隙，無重疊的平面F。多重平面磚必須N 重拼合成一個TE，然后整體平移鋪排構成F。

2 基礎平面磚TE

根據對稱性基本原理[9-10]，任何二維平面磚周期性地擴展形成的無窮大平面F 可視為平面點陣。任何平面點陣均可用元胞（unit cell）表示，而元胞的一般形式為廣義的平行四邊形P4。因此，所有TE的基形P 必為P4。根據對稱性，可將P4按邊及夾角分為傾斜Ob（Oblique，A，B，γ）、矩形Rt（Rectangle，A，B，90°）、四方Sq（Square，A，A，90°）、六方Hx（Hexagonal，A，A，120°）和棱形Rb（Rhombus，A，A，γ）。所有P4具有兩對平行等長的邊偶（Lateral couple，LC），表示為2A2B。

顯然，以元胞A，B，γ 定義的點陣內，一個任意有限面積的平面A 如果要成為TE的先決條件必須是：A 邊線上任一點p 必須在點陣內具有等效點p（nA，mB），其中n，m 為任意整數。

A 邊緣的任何變形將導致其局部的凸出或凹進。為滿足以上條件，其對邊必須相應地凹進或凸出，相當于一對LC 用完全相同的線替換。此即成為本文定義的TE。因此，將LC 用任意線同替換過程稱為“等盈虧”（Equi-Gain-Lose，EGL）操作，形成的新平面稱為EGLP。顯然，EGLP面積與元胞相同，但形狀和對稱性完全改變。任何P 可通過EGL 操作實現邊緣曲線化。圖3 以實例描述了EGL操作及產生的TE。

如P4用折線進行EGLz操作（下標z 表示折線zigzag），如圖3-a 所示，則P4變成含凹角的平行4+2n 邊形，含有2+n 對LC，可進一步進行任意線的EGL 操作。因為EGLPz的內角無限制，圖3-b，c，d 分別顯示不同P4經EGLz操作后可以形成三種不同對稱性的凸邊平行六邊形P6（2A2B2C，實際是含一個0°內角的平行八邊形）：H2（點群2）、Hm（點群2mm）和H6（點群6mm）。因P6具有特殊的對稱性，而且也能順二軸（三軸中任意二軸）簡單平移擴展成F，為方便計算，本文將TE的基形P 定義為P4和P6。

圖3 EGLP 構成TE 的實例

不同對稱性的P4可通過EGLz操作相互轉化。P4[A，B，γ] 可以通過兩步EGLz操作轉化為面積相同的P4’[A’，B’，γ’]。因為每步只能改變一個軸長，故需引入γ*。

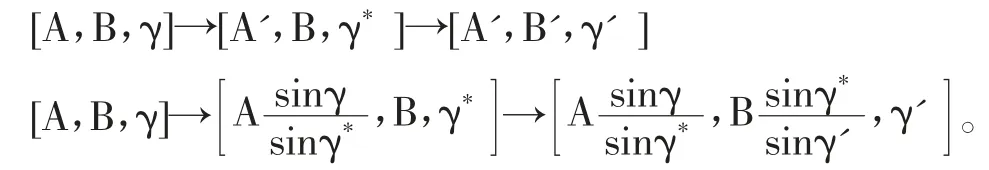
圖4 顯示了P4相互轉化的路線圖及按任一路線導致的形狀變化。

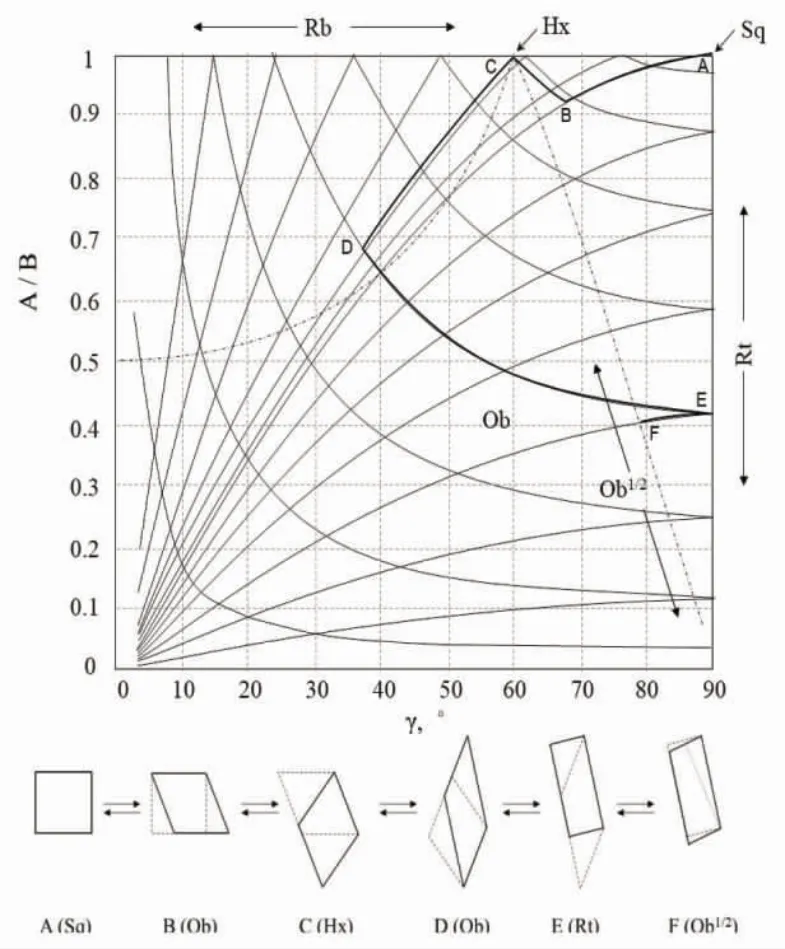
圖4 不同的平行四邊形P4 通過EGL 操作相互轉換路線圖

綜上所述，可以得到一般的結論：所有EGLP 均為TE；所有的TE必須是EGLP。此外，所有TE均可通過EGL操作相互轉化，或者說，同面積的TE構成一個無窮群。

3 TE 的對稱性

圖5 和圖6 通過一些實例，反映出TE對稱性的基本概況。

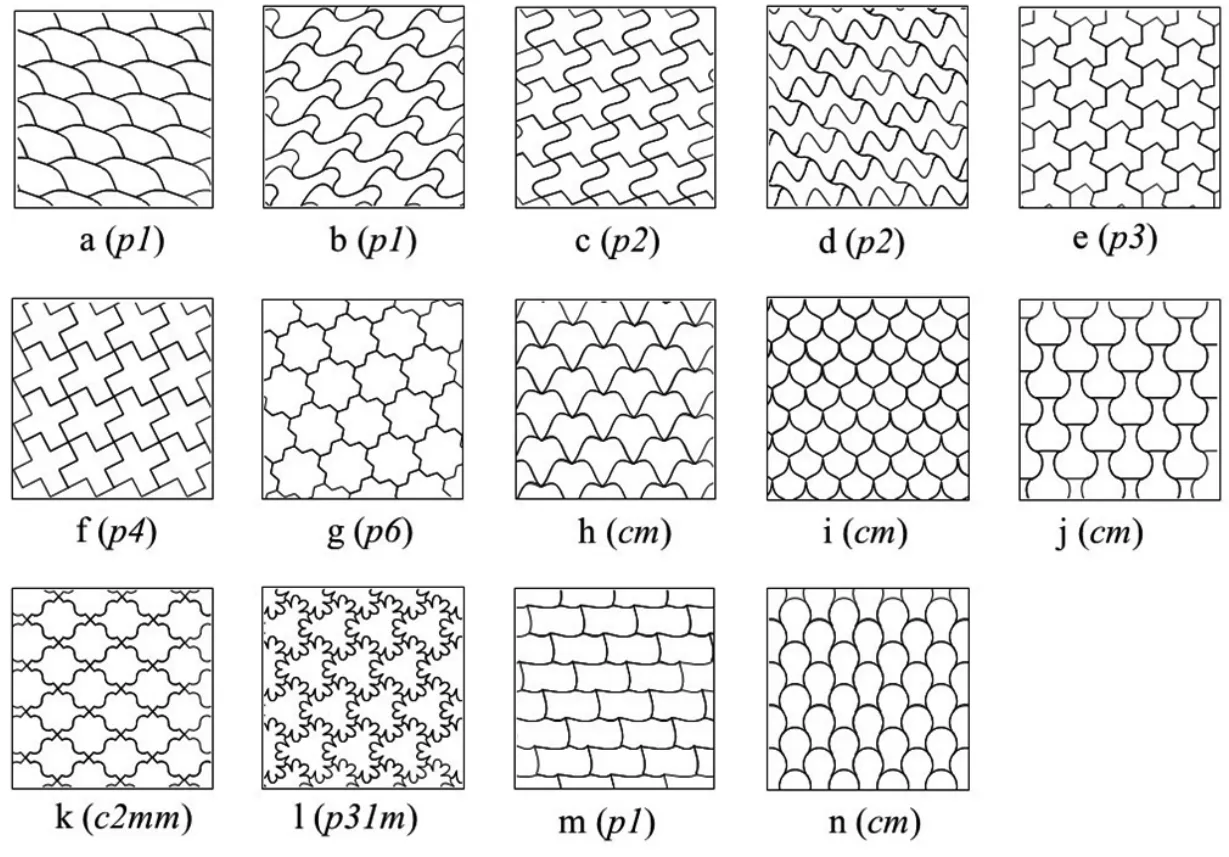
圖6 由圖5 中的TE 鋪排成不同平面群（括弧內）的F

所有的P 均具有旋轉軸Cn，有的具有鏡面m（Rt、Sq、Hx、Rb、H6、Hm）。P 經過任意線的EGL 操作形成2a2b（2c）（a、b、c 為不交叉的任意曲線，A、B、C 為與以上起點和終點相同的不交叉的折線。等邊P 中一般將不同任意線記為a 和a’）后，原則上所有的Cn和m 完全消失，TE的點群降為1，形成的F 的平面群降為p1（圖3-a，e，g 和圖5，6-a，b，m 為代表）。

如果對EGL 線條進行一定限制，則仍可保留P 的部分對稱性。以下為一般規律。

（1）全二重線A（線中點為二重軸）可以保留P 的Cn。如將C2對稱的P（Ob、Rt、Hx、Rb、Hm、H2）中的2A2B（2C）替換為2A2B（2C），則可保留C2，形成平面群p2（圖5，6-c，d 為代表）；對于C4對稱的Sq，4A（2A2A，兩組邊偶的夾角仍為90°）使其保留C4，形成平面群p4。類似，對于C6對稱的H6，6A（2A2A2A，相鄰邊偶的夾角仍為120°）使其保留C6，形成平面群p6。有趣的是，當采取由直線z 構成的z90°z90°z 的A對Sq 進行4A操作時，EGLP 產生新的m，形成4mm點群。與此相似，z120°z120°z 對H6 進行6A操作時，EGLP 也產生新的m，形成6mm 點群。但這兩種情況下，新的m 與原P 的軸不重合，無法帶入點陣，故為無效m，鋪排成F的點群仍分別為p4和p6（圖5，6-f，g）。

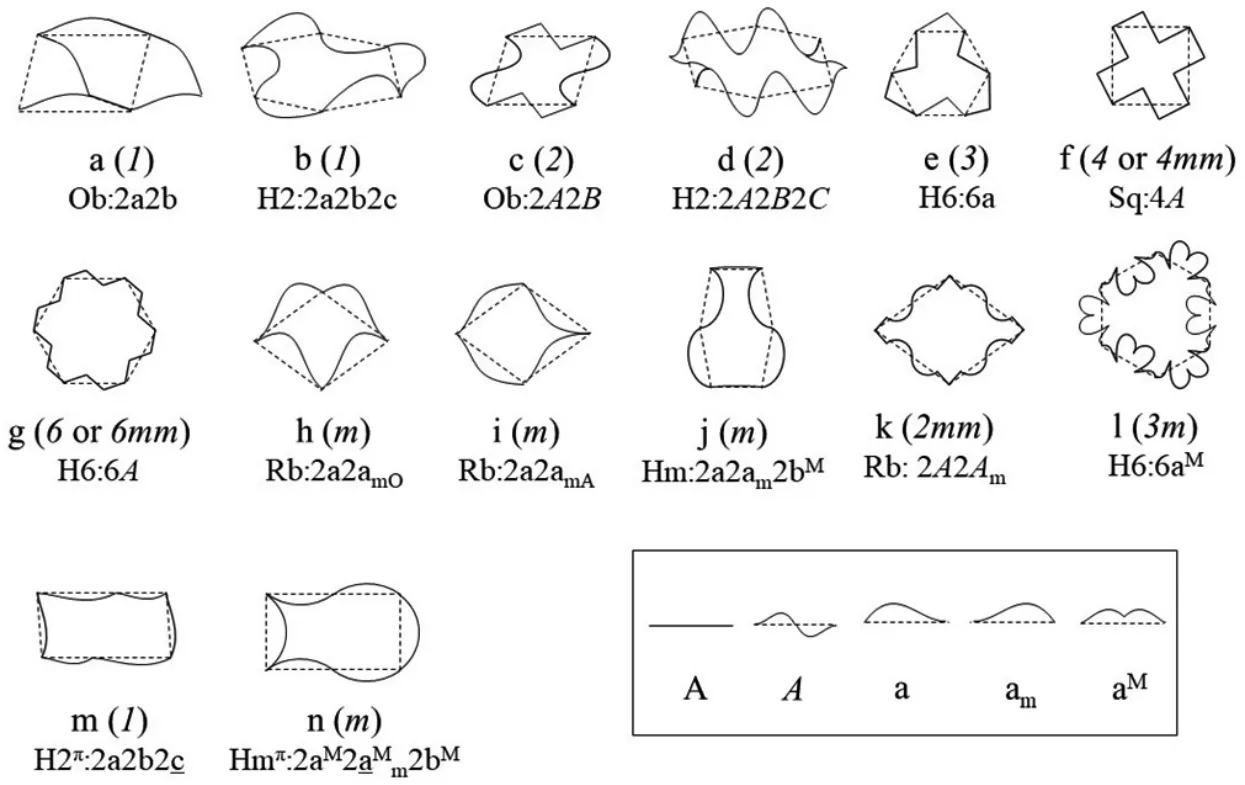
圖5 由不同P 和EGL 線條組成的幾種典型的TE（標號下方為P 及線條組成，括號內為所屬點群）

（2）對三個等軸P4（Sq、Hx、Rb）采取2a2am的EGL 操作可保留一個m。其中Hx 和Rb 根據m 的設置在鈍角（o）或銳角（a），有兩個異構體（圖5，6-h，i）。與此相似，對于Hm，采取2a2am2cM進行EGL 操作也可保留一個m（圖5，6-j）。

（3）對三個等軸P4（Sq、Hx、Rb）采取2A2Am的EGL操作，則不僅可保留C2，而且可保留兩個相互正交的m，達到高對稱性點群2mm，并形成c2mm的F。（圖5，6-k為代表）。

（4）H6 為最高對稱性的P，即使用任意線進行EGL操作（6a）仍能保留C3（圖5，6-e）。當用6aM（aM表示任意線中點為垂直基線的鏡面）進行EGL 操作后，則可保留C3和3 個m，形成3m點群和p31m平面群（圖5，6-l）。

（5）如果設置兩個對稱的180°內角，P6縮邊為P4。H2可以變成假Ob，記為H2π（圖5，6-n）。同樣，Hm 可以變為假Rt，記為Hmπ（圖5，6-m）。它們的曲線化的一般表示為2a2b2c（下劃線b 表示其與前邊共線）。縮邊P6作為TE形成不同的風格。Hmπ（圖5，6-n）可像Hm 一樣保留一個m，也可與后述的QRHpm一起描述出矩形磚的多種“錯位”砌墻形式。因為0°和180°內角導致的縮邊現象，多邊形（包括圖3-e，f）鋪排成F是否全接觸并非如圖2-d，e那樣一目了然。

以上有些TE部分保留了原有的m（圖5，6-h，i，j，k，l）或產生新的m（圖5，6-f，g）。這些非手性平面磚的正、反面相同。其余的TE均為手性磚，正反面互為對映體。

以上TE囊括了10 個點群，由此可以鋪排出具有不同空間群的F。但是因為P 的所有直線被曲線化，所以要求這些直線必須為m 的空間群，如pm、p2mm、p4mm、p6mm、p31m，不會在全曲線化的TE中出現。

4 多重平面磚TN

因為TE是唯一能夠僅通過平移而周期性地鋪排成F的平面，那么TN必須是TE分割為N 個相同形狀的平面之一。P 可能以多種方式均分割為多個凸邊多邊形。圖7 中陰影部分的P 和EGLPz以不同的方式均分割為多個直角正三角形，形成不同的平面群。這些三角形的邊緣是否可以全曲線化？什么樣的曲線才能夠滿足要求？

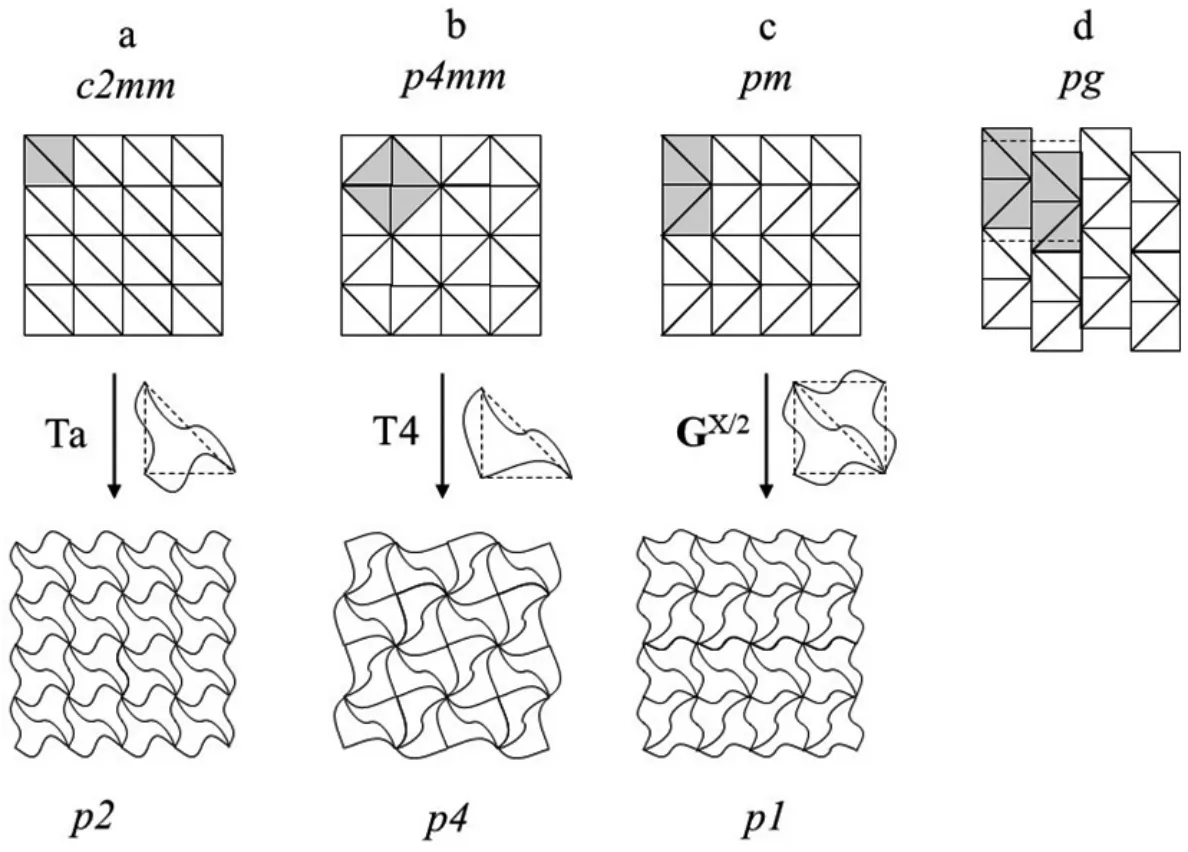
圖7 一個P 或EGLPz（陰影部分）被均分割為多個直角等腰三角形的幾種方式（其中a、b、c 的三角形可以不同方式（如后述）進行全曲線化；d 為非全接觸，不能曲線化）

相鄰的TE之間是簡單平移等效邊。而在一個被分割的P 內，相鄰多邊形之間則必須是旋轉等效邊，或者是鏡面等效邊。圖7-a，b 中，分割的P 具有旋轉軸，三角形之間分別互為C2（降低的軸次）和C4旋轉等效邊。分割后三角形的接觸邊不僅全接觸，而且接觸邊是固定的；而圖7-c，d 中，雖然也存在二重軸，但分割線并不全過軸心，導致接觸邊不固定。但圖7c 為全接觸，圖7d 為非全接觸。顯然，圖7-a，b 中過N 重旋轉軸心分割形成的N 個三角形最容易曲線化。

很多EGLPz也可以像P 一樣，按照不同的方式均分割為多個特定形狀的凸邊多邊形。要想使這些多邊形成為可曲線化的TN，所有相鄰多邊形也應為旋轉等效邊。所以EGLPz在分割時應像P 一樣保持最低旋轉軸，或遵守“過軸心N 分割”的規則。顯然，那些具有旋轉軸的r-EGLP（r，表示旋轉軸rotation）能夠成為產生TN的候選者。

因為平面點陣中允許的旋轉軸次只能是2、3、4、6，所以N 只能等于2、3、4、6。圖8 顯示了P 和一些r-EGLPz經“過軸心N 分割”形成凸角x 邊形（x=3、4、5、6，分別表示為T，Q，P，H）。顯然，這些x 邊形可以作為TN的基形G。圖8 橫線上方為本征G，其基本幾何特征用后續的數字或字母表示，如a（arbitrary）表示任意邊長和角度；p（parallel）表示有一對平行等長邊；數字3，4，6 分別表示相鄰的兩條等長邊之間的夾角為2π/3，2π/4，2π/6。

如前所述，P 具有兩對（或三對）平行LC：2A2B（2C），曲線化時同一對LC 必須進行任意線同替換的EGL 操作。從圖8 中可以看到，G 也存在曲線化時與等盈虧相關的LC。這些LC 可以是平行的（Qp、Pp、Hp），也可以具有60°、90°、120°夾角，分別記為26A、24A、23A。此外，G 還可能存在獨立邊（independent lateral，IL，可以單獨變化的邊），奇邊多邊形T 和P（x 分別為3 和5）必須具有IL。圖7-a 中C2的夾角為180°，故三角形沒有LC，三條邊A、A、B 均只能作為IL 分別用面積自盈虧的二重線A、A’、B變換。而圖7-b 的P 中存在C4，兩條90°夾角的等長邊為LC（24A），其可以替換為24a，而多余的一條獨立邊B 用B替換。因此，可將G 的曲線化必須的等盈虧操作（EGLN操作）定義為：LC 在保持夾角的前提下由任意曲線a 進行同替換；IL 由任意二重線A替換。需要強調的是，某一個TN只適合于所產生的P 或EGLPz。如圖7 所示，三角形曲線化后只能分別按a、b 的方式原樣拼合。

從圖8 可見，所有G 中，除了Ta 和Qa 無LC，分別有3 和4 條IL 之外，其余的G 均具有1~3 對LC。按照EGLN操作的規則，每個G 圖形下方標明了x 條邊對應的一般曲線，或自由度最大的曲線。

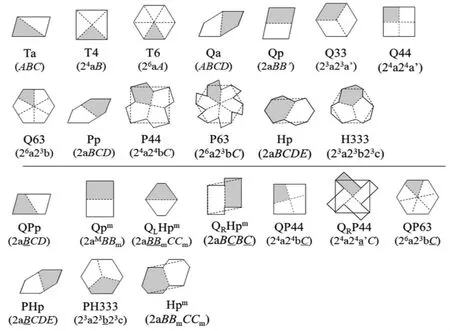
圖8 P 或EGLPz 按照“過軸心N 分割”規則得到的多邊形G（陰影部分）（橫線上部為本征G，下部為衍生G。圖形下方為G 的命名，括號內為LC 和IL 及其相應的等盈虧線條）

圖9 為本征G 按照EGLN規則曲線化并拼合后鋪排形成的F及其空間群。容易判斷，圖1-c 中曲邊磚的基形為H333。因為EGLN操作時均采用一般曲線，不存在含m的點群和空間群。

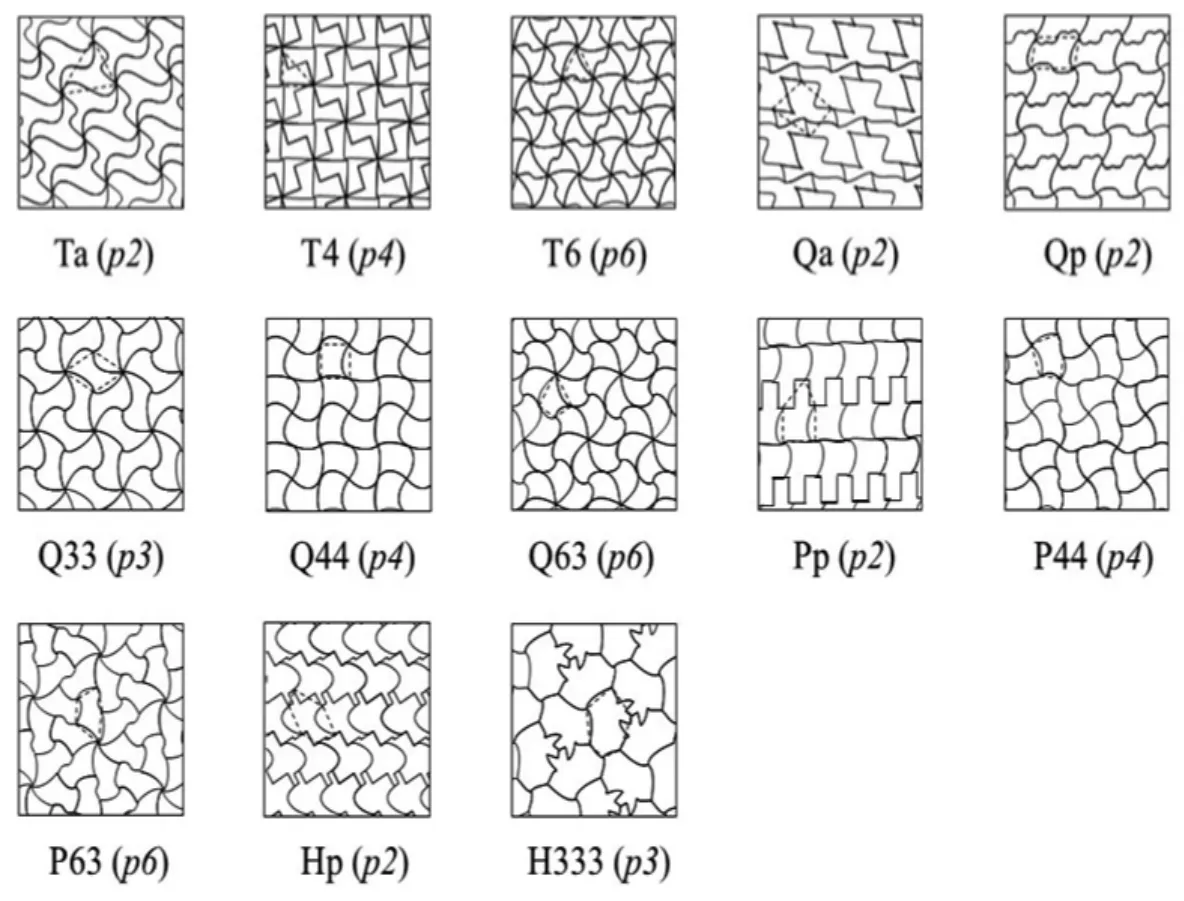
圖9 圖8 中的本征G 經EGLN 操作得到的TN 及其拼合鋪排成的F（括號內為平面群）

圖8 橫線下方為衍生G，其邊的組成與本征G 相同，但其中可能因180°內角導致的縮邊，如表觀四邊形實際為五邊形表示為QP；假五實六表示為PH，假四實六表示為QH 等。衍生G 還包含了通過幾何限制增加對稱性的情況，如通過限制邊長和角度，同時將一般曲線改為限制曲線，使Hp 增加一個鏡面，變成Hpm等。

還需要特別指出的是，有些G 在滿足基本幾何關系下可以產生較高對稱性，如Pp、P44、H333、PH333 等可能產生m，鋪排成高對稱性的F。但可惜的是因為存在與m垂直的IL，故EGLN全曲線化操作時，無論對曲線如何限制，這些m 均不可能再存在，故不列入衍生G 清單。圖10 為衍生G 經EGLN操作并拼合后鋪排形成的F及空間群。其中包括G 的幾何形狀無變化，僅將一般曲線改為限制曲線后提高了對稱性的Q33m（23a23am）、Q44m（24a24am）、Q44mm（4aM）。

G 通過EGLN操作后，面積無變化，LC 和IL 曲線化導致的盈虧部分拼合時正好互補。這樣可以形成無窮數量的EGLG。由此得出一般規律：所有EGLG 均可作為TN。

有些TE之間也可以不作為平移等效面，而是作為旋轉等效面而構成TN。如Sq（2a2a）與Q44（24a24a，N=4）同形；Hx（2a2amo）與Q33（23a23a，N=3）同形；Hmπ（2aM2aMm2bM）與Qpm（2aMBBm，N=2）同形。還有一些T，既能作為TE，也能作為TN。甚至作為后述的TNX。

在圖10 中，除了7 個標明m 的TN之外，均必為手性TN。一般情況下，手性對映體是不可混拼的，只有一些具有特殊線條的EGLG 對映體可以混拼，相當于化學中的外消旋體晶體。因本文的T 僅限單面，故將混拼對映體問題留待以后討論。

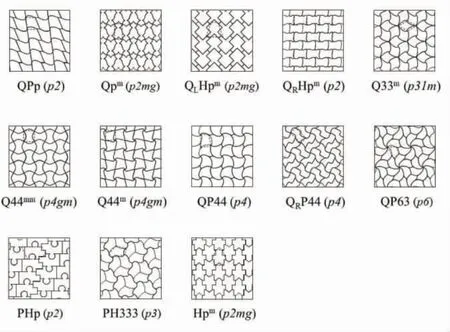
圖10 圖8 中的衍生G 經EGLN 操作得到的TN 及其拼合鋪排成的F（括號內為平面群）

5 等邊多重平面磚TNX 和復合等邊多重平面磚TNX/2

如同圖2-d，e 和圖7-d 那樣，不（或不能）按照“過軸心N 分割”規則也有可能分割出N’個相同的凸角x 邊形。因與軸心無關，N’沒有N 的限制。這些任意分割出的多邊形既無LC，也無IL，很多是非全接觸，表示為GA（上標A 表示Abnormal）。因為GA不可能進行EGLN操作，故不能曲線化。Grünbaum[5]列舉了幾個極富想象力的凸角五邊形或六邊形GA。（任意三角形或四邊形能夠分別以Ta 和Qa 的G 形式拼合并鋪排成F）。

導致以上現象的本質是TN在拼合時必須保持絕對的全接觸，這需要EGLG 各曲邊之間的拼合是固定搭配的：LC 找同樣的LC，IL 找同樣的IL。“過軸心N 分割”規則可以很好地保證這種固定搭配。而任意分割的多邊形并無固定搭配，如不能保證全接觸，就不能曲線化。但是，很多等邊多邊形（Equilateral x-gon，GX）能夠實現全接觸，故不需要固定搭配，那么“過軸心N 分割”規則就不是必要的了。事實上，x-邊形的GX只要是來自P 或者EGLPz，都可以在保持內角不變的條件下用x 個相同的二重線全替換（這是GX曲線化的唯一途徑，稱為EGLD操作），成為曲邊的TNX。圖11-a，b，c，d，e 為TNX實例（其中d、e 可視為G6）。

在前述的P 和G 中也有一些GX，如Sq、Rb、Hx、T6（N=6）、Q44（N=4）、Q33（N=3）；邊長或角度限制的GX，如Pp（2*90°，60°）、Hm、H2、Hmπ、H2π、P44（2*114.3°，131.4°，N=4）等。它們具有LC，可以引入任意曲線。當然也可以用相同二重線全替換，這與EGL 或EGLN操作的規則是一致的，屬于正常的TE或TN。

但是，如圖7-c 和圖11-f，g，h，i，j 所示，有些P 可以按任意方式分割成多個特殊形狀的三角形或四邊形，相鄰的兩個多邊形正好拼成一個等邊多邊形（相當于一個GX再次分割），此即為半等邊多邊形GX/2。GX/2也可以進行EGLD操作而全曲線化（等長邊用相同的二重線替換，分割線為獨立邊，用單獨的二重線替換）。有意思的是，GX/2不必按照分割時的模式原樣拼合，而可以多種模式拼合出很多圖案，如Sq 作為GX分割為兩個直角正三角形（GX/2），經EGLD曲線化后，可以拼合出以圖7-c 和圖11-f，h 為例的很多種圖案。

值得注意的是，一些多邊形可以充當多種角色的T。如邊長1∶2 的矩形（2mm）。既可視為Rt（2a2b），或者Hmπ（2a2a'2a"）充當TE；也可視為QRHpm（2aBCB'C'）或者QRP44（24a24a'B）充當TN（N 分別為2 和4）；還可以視為等邊多邊形（G6）充當TNX（N 為大于1 的任意數）構成許多圖案，如以圖1-b（圖11-d，e）等為代表的多種方磚鋪地藝術。

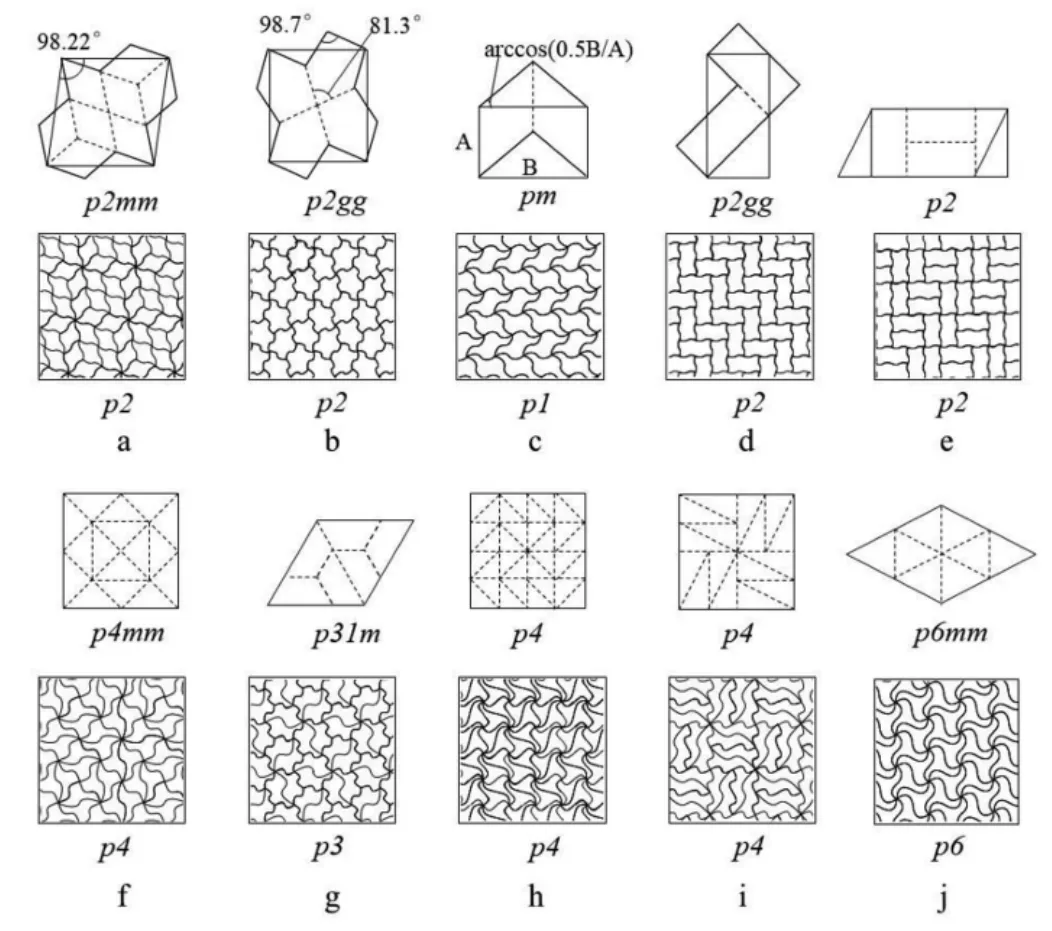
圖11 EGLPZ 未按照“過軸心N 分割”規則分割成N’個等邊多邊形（GX）及其TNX 拼合鋪排圖，a-e；P 任意分割成多個半等邊多邊形（GX/2）及其TNX/2 的拼合鋪排圖, f-j

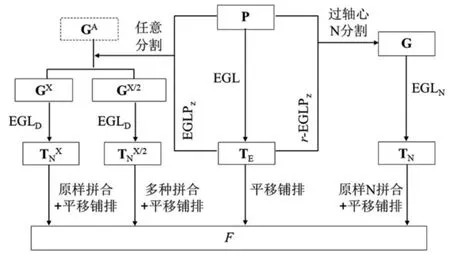
圖12 不同曲邊單面單磚的形成及其相互關系

6 結論

根據平面點陣理論，可嚴密鋪排成無窮大平面F的點陣型平面單磚（包括異形、曲邊等復雜平面）的最基本形狀為平面群的元胞。本文提出的單形，單面，曲邊平面磚T 分為基礎平面磚TE和三種多重平面磚TN、TNX和TNX/2。其中TE可順兩個方向平移鋪排成F；多重平面磚需要多重拼合成為TE。T 建立的一般過程是以一個凸角多邊形作為基形，然后在保持基形面積不變的條件下按一定規律將所有直線曲線化。TE的基形P 包括不同對稱性的5種元胞和3 種凸角平行六邊形。P 的曲線化必須通過平行邊偶（LC）用任意線同替換，使P 的凹凸面互補的等盈虧（EGL）操作來實現。由此得出結論：所有EGLP 均為TE，所有TE必須是EGLP，不同的TE可以通過EGL 操作相互轉化。

P 或者具有旋轉軸的折線型r-EGLPz按照“過軸心N 分割”的規則可得到N 個（N=2，3，4，6）相同的凸角x邊型（x=3，4，5，6），其可作為TN的基形G。G 存在0~3對LC 和0~4 條獨立邊（IL）。其中LC 包括平行LC（0°夾角）和2π/6、2π/4、2π/3 夾角LC。G 的曲線化也需要進行相應的等盈虧（EGLN）操作：LC 用任意線同替換，IL 用二重線替換。

實際上，P 和很多EGLPz也能夠不按照“過軸心N分割”規則分割成N'個相同的多邊形，除了等邊多邊形（GX和GX/2）之外，一般不能全接觸，不能進行EGLN操作，故不能全曲線化，只能以非全接觸多邊形GA的形式拼合鋪排為F。

等邊x 邊形GX可以在保持原來角度的條件下用x條相同的二重線全替換（EGLD操作）實現曲邊化，形成TNX。P 和很多EGLPz也能夠以任意的方式分割出多個由特殊的多邊形GX/2拼成的半等邊多邊形。GX/2含有2-3 條等長邊和1 條獨立的分割邊。其也能進行類似上述的EGLD操作（等長邊由相同二重線替換，獨立邊由單獨二重線替換），由此形成的TNX/2可以拼合成多種不同對稱性的圖案。

圖12 總結了各種T 之間的邏輯關系。本文的核心依據是平面點陣理論以及由此推斷的不同分割方法和等盈虧操作方法。從此人們可以理解、判斷并預測所有異形多邊形及其曲邊化產物的平面特性；可以設計出不同對稱性，不同風格的多邊形及全曲邊平面磚。