基于ADAMS的滑塊連桿固定型機構動力學仿真分析*

馬浩浩，馮彥偉，姚寶珍

(天水師范學院，甘肅 天水 741001)

0 引 言

對機構運動分析在機械設計中具有重要意義，無論開發新機械，還是了解現有機械的動力學性能都是十分重要的。機構的運動分析主要內容是在根據已知的結構參數及原動件的運動規律求解該機構的某些構件上點的位移、速度、加速度、運行軌跡和構件的角位移、角速度、角加速度及工作過程受力分析、做功、能量轉化等。平面機構的運動分析主流方法有圖解法和解析法，在求解中往往多種方法并行求解，通過對結果分析，繪制運動圖線，以更好的解決工程實際問題[1]。筆者選擇幾種滑塊連桿固定型平面四桿機構，分別采用圖解法與解析法對機構運動分析，并借助ADAMS軟件機構動力學仿真分析，通過分析計算、結果對比，以更加靈活的掌握平面機構運動分析的方法，更好的指導機構創新與應用，具有較高的實踐指導意義。

1 滑塊連桿固定型平面四桿機構分析

平面連桿在工程應用中應用廣泛，如工業機器人、機器臂、機械手、各類展開機構、折疊機構及仿生關節等中均有應用，其中平面四桿機構結構最為簡單，加工制造容易、工作使用可靠[2]。

文中在選定兩種特殊平面四桿機構加以分析研究，均為滑塊連桿固定型機構，運動簡圖分別如圖1中(a)、(b)所示。機構原動件數為1，活動構件數為3，低副數為4，髙副數為0，故機構的自由度為：

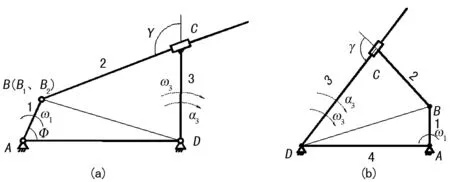
圖1 滑塊連桿固定型機構運動簡圖

F=3n-2Pl-Ph=3×3-2×4=1

故該機構具有確定的運動。圖1(a)較為常見，圖1(b)為圖1(a)機構的結構模仿與創新，其具有類似求解方法，后續均以圖1(b)為研究對象加以運動分析和動力學仿真。

2 解析法作機構運動分析

選用復數矢量法解析機構的運動特性，通過建立機構的位置方程，再對時間求導分別作機構的速度、加速度分析[3]。

2.1 建立位置方程

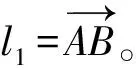
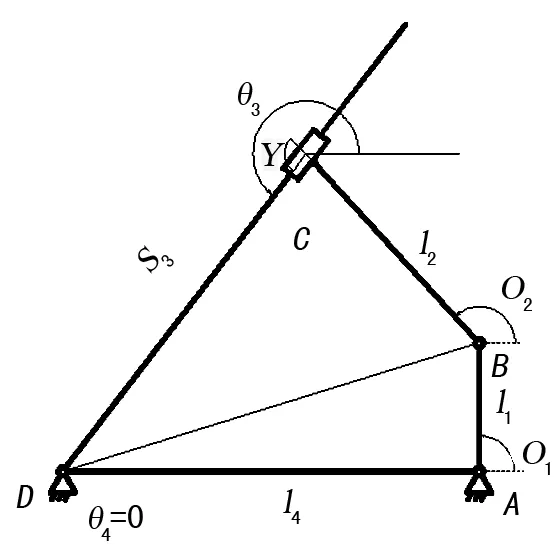
圖2 封閉矢量多邊形

原動件1的運動規律和各桿的長度已知，即確定l1、l2、l4、θ1的參數，θ4=0，θ3=θ2+γ，l3為變量，s3=l3。由此建立構件的封閉矢量方程為：

l1+l2+s3+l4=0

(1)

2.2 復數矢量法求解

采用復數矢量形式表示構件的封閉矢量方程為：

l1eiθ1+l2eiθ2+s3eiθ3+l4=0

(2)

應用歐拉公式eiθ=cosθ+isinθ分離方程式(2)的實部和虛部，得：

l2cosθ2+s3cosθ3=-l1cosθ1-l4

(3)

l2sinθ2+s3sinθ3=-l1sinθ1

(4)

求解式(4)，可得：

s3=-(l1sinθ1+l2sinθ2)/sinθ3

(5)

將θ3=θ2+γ代入式(3)，可以整理并簡化為：

Asinθ2+Bcosθ2+C=0

式中：A、B=(l1、l2、l4、θ1、γ)T，C=-l2sinγ

可以解得：

在求得θ2后，由θ3=θ2+γ可求出θ3，代入式(5)可求s3。

速度分析時將式(2)對時間t求導，可得：

(6)

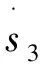
加速度分析時將式(6)對時間t求導，可得：

(7)

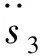
3 ADAMS動力學仿真

用解析法求解機構的運動分析的核心是位置方程的建立與求解，再進一步求導可進行速度和加速度分析，計算中涉及求解非線性方程組及線性方程組的問題，難度較大。文中再選用動力學分析軟件ADAMS對該機構做運動仿真分析[4]。

3.1 機構模型構建

建立圖1.1(b)所示的滑塊連桿固定型機構運動，選取機構參數為：連桿AB長240 mm，AD長780 mm，CD長480 mm，γ=100°，設定原動件1的角速度為30(°)/s，延逆時針回轉。

在ADAMS動力學仿真軟件中構建機構運動模型，共4個構件，4個關鍵點，構件的材料類型默認為steel，密度：7.801E-06 kg/mm3。為方便求解桿3的運動參數，選D點為坐標0點，機構關鍵點初始坐標值如表1所列。

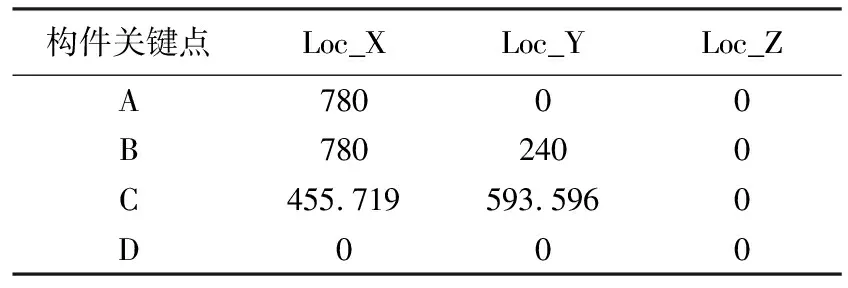
表1 機構關鍵點初始坐標值

桿4為機架，即AD固定；桿1為原動件，轉動中心為A點；滑塊與連桿固定的桿2繞B點轉動，滑塊沿桿3移動；桿3的轉動中心為D點。由此建立該機構的虛擬樣機如圖3所示。

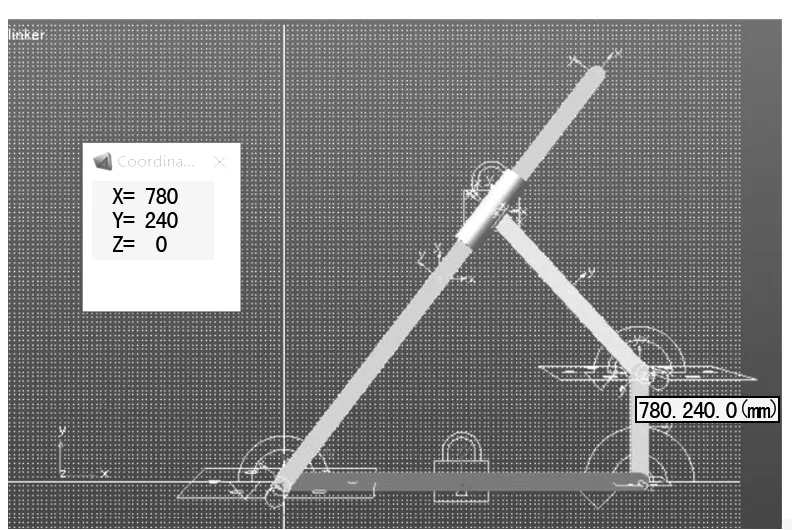
圖3 滑塊連桿固定型機構虛擬樣機

3.2 模型求解和數據后處理

原動件桿1添加旋轉驅動，定義數值為30.0d*time。設定終止時間12 s，回轉一個周期，步數600。仿真出桿3的運動規律，一個周期內桿3角速度變化曲線如圖4所示，角加速度變化曲線如圖5所示。

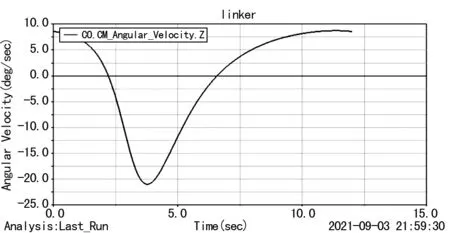
圖4 桿3角速度變化曲線

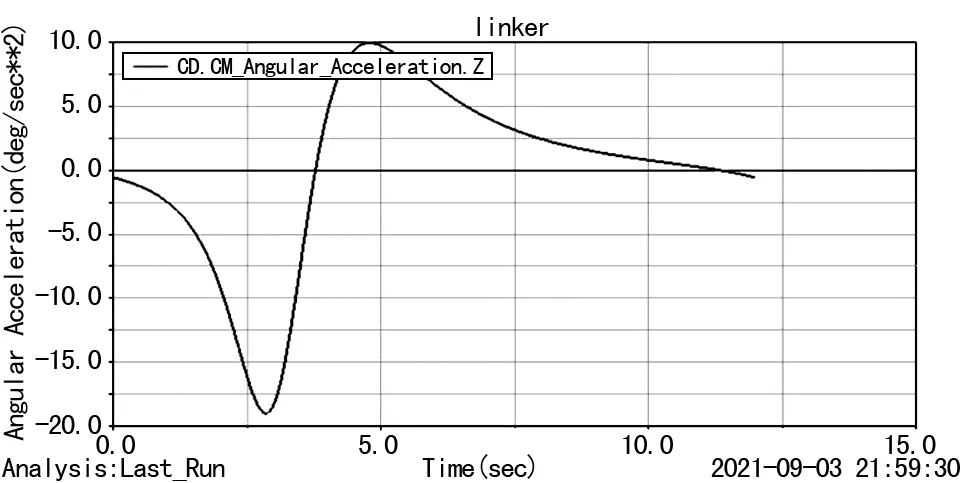
圖5 桿3角加速度變化曲線

在解析法求解機構的運動分析時，θ1為原動機桿1對應的方位角，θ3=θ2+γ，對于桿2的方位角θ2也可通過軟件仿真求解。由于B點為動點，在求解方位角θ2時采用反轉法，構件一經過B點的水平構件，使其與桿1鉸鏈連接與B點處，附加-ω1即可方便求解方位角θ2的數據，變化曲線如圖6所示。

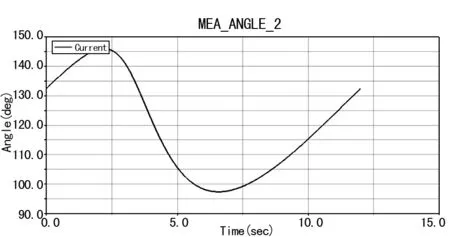
圖6 桿2方位角θ2的變化曲線

由θ3=θ2+γ，本算例中γ=100°，可求解出桿3的方位角θ3的變化曲線。同時，方位角也可以按照θ3=∠ADC+180°計算。如圖7所示，與圖6中所示的桿2方位角θ2的變化曲線相差γ值，經驗證該機構運動仿真正確，解析法求解計算合理。

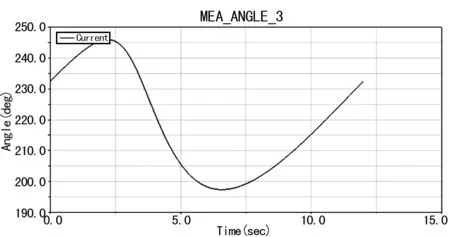
圖7 桿3方位角θ3的變化曲線

通過動力學仿真求解桿1與機架的連接鉸鏈處(A點)的反力，如圖8所示，(a)為驅動件桿1鉸鏈作用反力X方向分量，(b)為驅動件桿1鉸鏈作用反力Y分量。

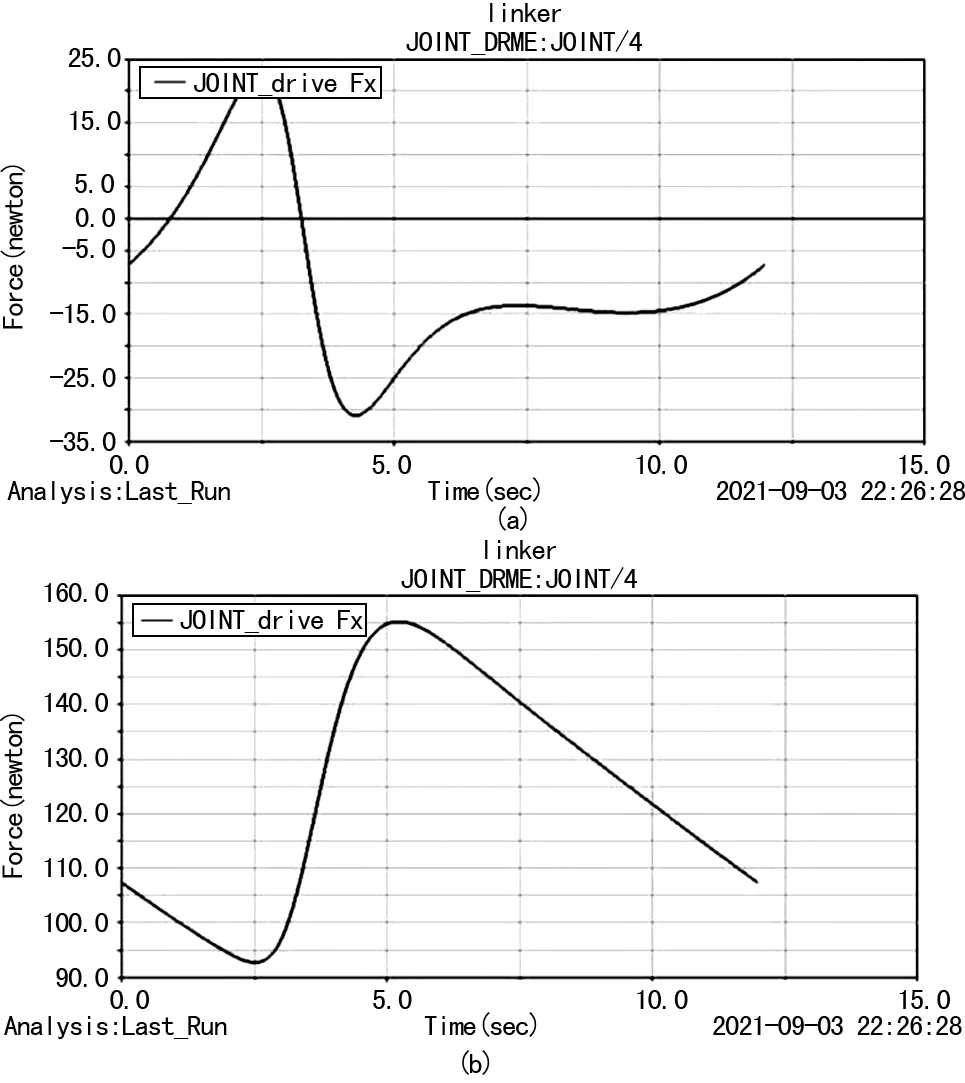
圖8 驅動件桿1鉸鏈作用反力的變化曲線

搖桿3鉸鏈作用反力X方向分量變化曲線如圖9(a)所示，Y方向分量變化曲線如圖9(b)。

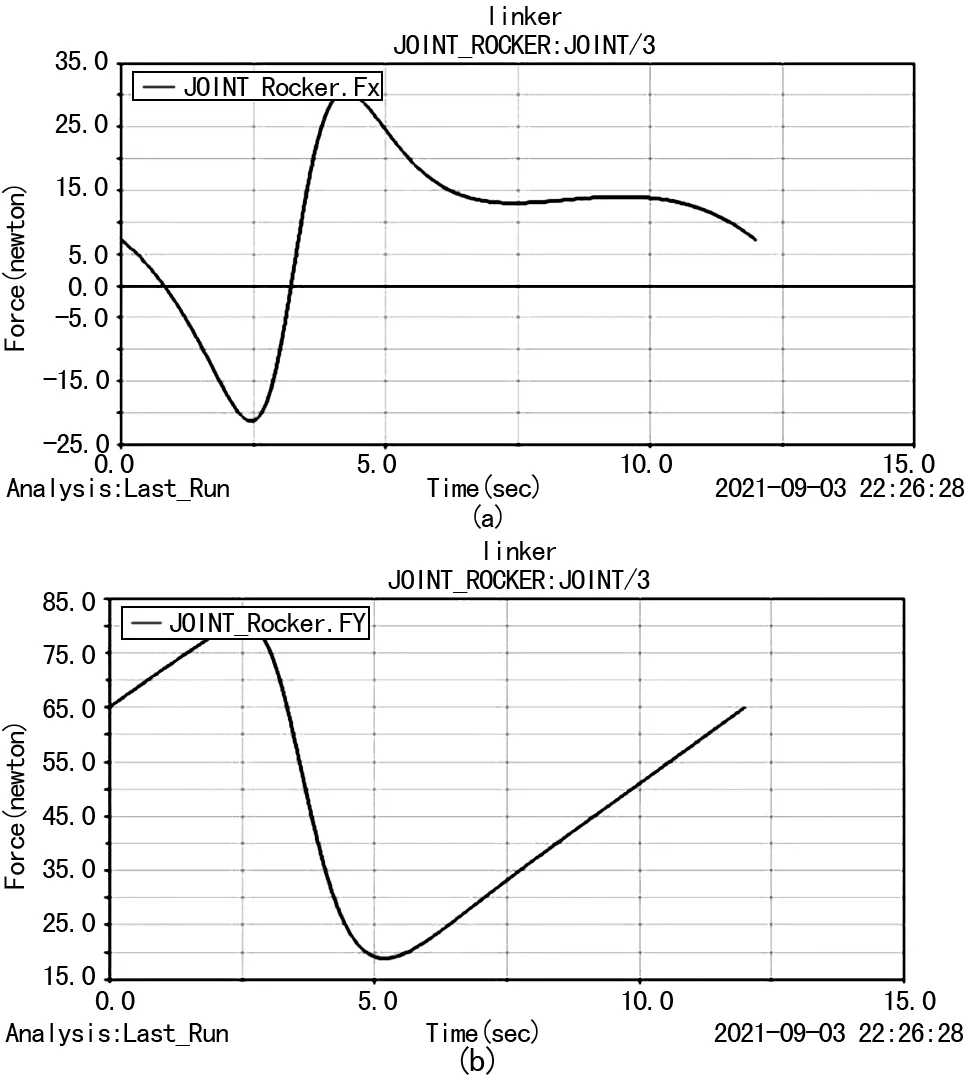
圖9 搖桿3鉸鏈作用反力的變化曲線

4 結 語

針對滑塊連桿固定型平面四桿機構分析研究，通過解析法與應用ADAMS多體動力學仿真分別作了滑塊連桿固定型平面四桿機構的運動分析。用解析法求解機構的運動分析計算中涉及求解非線性方程組及線性方程組的問題，難度較大；應用ADAMS多體動力學仿真軟件對機構各構件的角速度、角加速度、鉸鏈反作用力等數值計算[5]，對復合矢量法求解中的方位角也加以分析，對機構的急回特性加以研究，數值精準。對比結果表明：機構運動仿真求解計算合理，為機構分析提供求解分析方法，為后續機構設計改進、機構應用、產品開發提供有力數據支撐。