基于不確定性的航空裝備體系保障性評估

崔利杰，叢繼平，丁剛，任博，3，王毅，黎紀宏

（1.空軍工程大學裝備管理與無人機工程學院，西安 710051； 2.空軍工程大學研究生院，西安 710051；3.光電控制技術重點實驗室，洛陽 471000； 4.中國人民解放軍 95825部隊，孝感 432100）

航空裝備體系是一個包含裝備、人員、環境等因素的復雜巨系統。航空裝備體系的保障能力直接影響和制約著航空裝備體系的戰斗力，有效評估航空裝備體系保障性一直以來都是航空裝備領域的關注重點之一［1］。由于航空裝備體系保障本身存在的復雜性、耦合性和動態隨機性，解析法很難對其保障性進行準確有效地衡量。現階段對于航空裝備體系保障性分析主要以系統運行流程為切入點，構建相應仿真模型來模擬真實保障流程［2-4］。多Agent仿真理論和方法有效地實現了復雜系統運行過程仿真［5-6］，如NetLogo、Swarm、Anylogic等多Agent仿真軟件也為建模過程提供了便利條件。在國內裝備保障領域，上述軟件已在通用裝備保障體系［4］、陸軍裝備保障體系［2］、艦載機保障體系［3］方面進行了應用；但同時需要指出的是，這些仿真模型對于保障要素的描述仍停留在確定性層面［3］或是簡單地將其處理為隨機變量［2，7］，其輸出結果與實際結果存在一定偏差，一定程度上降低了仿真的可信程度和指導意義。近年來，各種不確定理論如考慮客觀因素的隨機分布理論，考慮主觀因素的如區間理論［8］、證據理論［9］、模糊理論［10］等方法的提出，為裝備體系保障性中不確定變量的描述和分析提供了理論和方法支撐。目前的保障仿真研究還集中于對主要涉及的部件故障率分布這一不確定性因素進行描述，且多限于簡單的隨機分布［11-14］，缺少對主觀因素考慮或處理相對簡單，如文獻［15-17］將維修保障中的維修間隔時間以隨機分布進行處理。在現代戰爭時效要求高、響應速度快、結果要求準的戰訓保障仿真需求下，如何合理、快速、精準地給出裝備體系仿真輸入輸出關系，是保障仿真推演的重大現實問題。

本文首先通過梳理航空裝備體系保障流程，構建出基于多Agent的航空裝備體系保障仿真系統，分析其中影響體系保障仿真結果的各類影響因素。其次，針對不同類別的不確定性因素，采用混合不確定性理論進行描述，并基于信息更新理論對其中的動態變量進行動態化的參數估計。然后，以得到的混合不確定性變量提出考慮不確定因素影響的航空裝備體系保障仿真方法，運行并輸出對應的保障性指標，進而采用多項式擬合方法對所得結果進行擬合，大幅縮短評估航空裝備體系保障性時間。最后，以一次典型戰訓任務過程中裝備體系的完好率為指標來驗證所提方法的可行性和準確性。

1 航空裝備體系保障性仿真建模

1.1 航空裝備體系保障流程

航空裝備體系保障流程由任務下達、任務執行、保障效果評估3個部分組成［18］。在任務下達環節，作戰指揮部門通過文件、規程等對機務指揮部門下達訓練任務目標和相關要求，機務指揮部門根據上級指示，考慮在作戰訓練過程中的各個因素，規劃飛機出動、定檢、大修、換發、排故等安排，通過指令工卡將相關任務要求傳達給各個業務部門；在任務執行環節中，由保障機組根據飛機使用計劃完成使用保障任務，技術保障人員在使用保障過程中隨時做好排除故障的準備工作，實施修復性維修，同時修理單位根據各類飛機壽控參數（如飛行小時、飛行起落等）進行定檢、換發、大修等維修保障工作，在這些保障活動中可能需要進行維修備件、維修裝設備、設施的請領及車輛等保障資源優化配置等工作；最終，所有保障工作應以文檔和數據形式進行記錄，實施保障質量控制、可追溯管理等維修效果評估工作。具體的航空裝備體系保障總體流程如圖1所示。

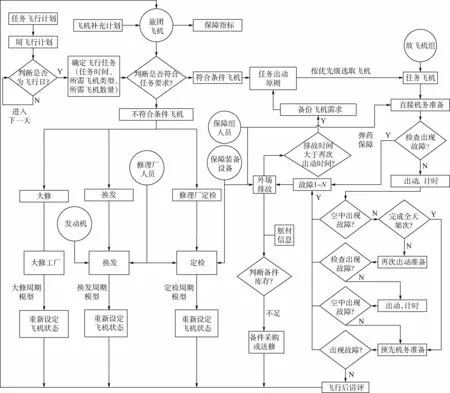
圖1 航空裝備體系保障流程Fig.1 Aviation equipment system support process

分析圖1可知，影響航空裝備體系保障效率的參數可分為4類：

1）戰訓任務參數，包括年總計劃飛行時間、飛行批次、飛行日安排和飛行架次等。

2）裝備可靠性參數，包括故障率、工作壽命等，可以用平均故障間隔時間（Mean Time between Failures，MTBF）、故障發生時間來衡量。

3）維修性參數，包括維修工作所需時間、大修、定檢能力、定期維修保障工作周期等，可以利用在一定保障資源約束下維修保障活動的工作持續時間來衡量，如定檢時間、大修時間、排故檢修時間等，其中大修在軍機保障過程中對飛機完好率起到了重要作用。

4）保障性參數，用來衡量備件、保障裝設備等資源的請領、延誤及到達情況，可以用車輛申領時間、備件延誤時間、車輛到達時間等來表征。

上述參數描述如表1所示。

表1 航空裝備體系保障流程參數描述Table 1 Aviation equipment system support process par ameter description

對于航空裝備體系保障流程的輸出，人們關注更多的是每日能夠參訓飛機的數量、完成任務的程度和能夠持續出動飛機的能力。一般地，可以將任務可靠度、飛機完好率或可用度作為衡量航空裝備保障能力的重要體現。以飛機完好率為例，其定義和計算公式表示如下。

飛機完好率指的是在規定使用條件和維修方案下，一個機型在一段時間內飛機完好架日與飛機實有架日的比值［19］。

式中：W為飛機完好率；J為一段時間內飛機飛行總架日；Nf為飛機不完好架日。

飛機完好率等指標當前主要采用式（1）進行統計分析，但在實際過程飛機不完好狀態往往受多種要素影響，因此可以將飛機完好率作為航空裝備體系保障仿真模型的輸出，將各類輸入變量作為仿真模型的輸入，由此得航空裝備體系保障仿真模型的函數表達如下：

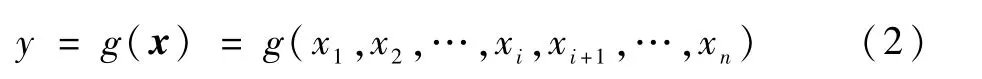
式中：y為保障流程輸出；x表示n維隨機變量，代表的是影響航空裝備體系保障性的n個變量，如分系統故障率、大修時間、定檢時間、檢查時間等；g（x）表征航空裝備系統運行或仿真的整個過程。

1.2 基于多Agent航空裝備體系保障性仿真建模

考慮到航空裝備體系保障流程設計因素多、相互間關系復雜，部分組成要素自身屬性多樣且與其他組成要素間存在相互間影響，本文采用多Agent建模方法對航空裝備體系保障流程進行仿真建模。

在多Agent仿真模擬軟件中，NetLogo以其開源、易操作、多主體可操作性等特點適于研究時變的多Agent系統。NetLogo基于Java環境進行開發，其中主要包含4種Agent：turtle、patch、link和observer［20］。通過提供基礎的Agent類型為建模構建了易操作理解的平臺，為觀察分析不同條件下的多Agent模型的相關工作活動進程提供了輔助支持。利用NetLogo軟件可進行多場景實驗管理，適用于航空裝備保障這類復雜系統。因此，本文基于Netlogo平臺，參考圖1所示的航空裝備體系保障流程，構建如圖2所示的航空裝備體系保障仿真系統。

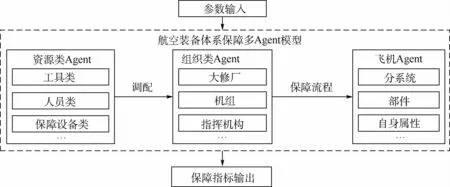
圖2 航空裝備體系保障仿真系統Fig.2 Aviation equipment system support simulation system

將航空裝備體系保障流程中涉及到的各個組成部分分為3類Agent：資源類Agent、組織類Agent、飛機Agent，將戰訓任務參數、裝備可靠性參數、維修性參數及保障性參數作為Agent屬性進行輸入，飛機完好率等保障指標為輸出，按照圖1保障流程規劃Agent交互規則來實現仿真運行。

2 仿真不確定性分析

根據實際工作可將表1所示的影響因素分為確定性變量及不確定性變量。其中，確定性變量包括飛機的飛行時間、數量，工作人員數量，航材初始數量，大修廠、修理廠修理容量等因素，這類變量一般不會在短期發生變化；不確定性變量主要涉及飛機的故障率、大修時間、定檢時間、飛行前檢查時間等變量，這些變量在保障過程中經常受各種原因而難以準確描述的因素。例如，裝備機件故障這種多由于自身固有原因和環境影響造成，可視作客觀不確定性變量，用隨機變量來描述。而由于人員、組織、管理等原因引起的各類修理時間、延誤時間等因素，多是人們對客觀事物的認知不足，可視作為主觀不確定性變量，用模糊變量來描述。通過采用不確定性變量方式對仿真系統所涉及的不確定性因素進行描述，相較于采用統計數據得到的固定的參數描述，擴展了仿真系統的作用，在得到輸出結果的基礎上可以進一步研究不確定性變量對輸出結果的影響程度。由此，根據式（2）重新定義航空裝備體系保障流程輸入輸出關系為

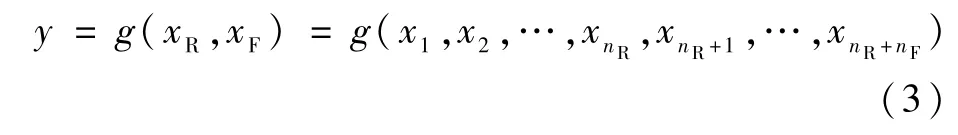
式中：x1，x2，…，xnR為nR維隨機變量，代表的是影響航空裝備體系保障性的nR個客觀不確定性變量，xnR+1，…，xnR+nF為nF維模糊變量，代表的是nF個影響航空裝備體系保障性的主觀不確定性變量。

2.1 客觀不確定性變量描述

如前所述，針對客觀不確定性變量，可按照NLFR模型［15］求解其參數，具體過程如下。

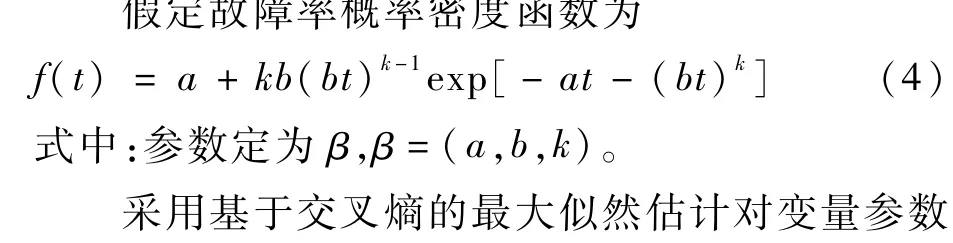
為確定使對數似然函數最大化的β的估計，采用交叉熵算法對β進行優化估計，通用的交叉熵算法可參見文獻［21］。

2.2 主觀不確定性變量描述

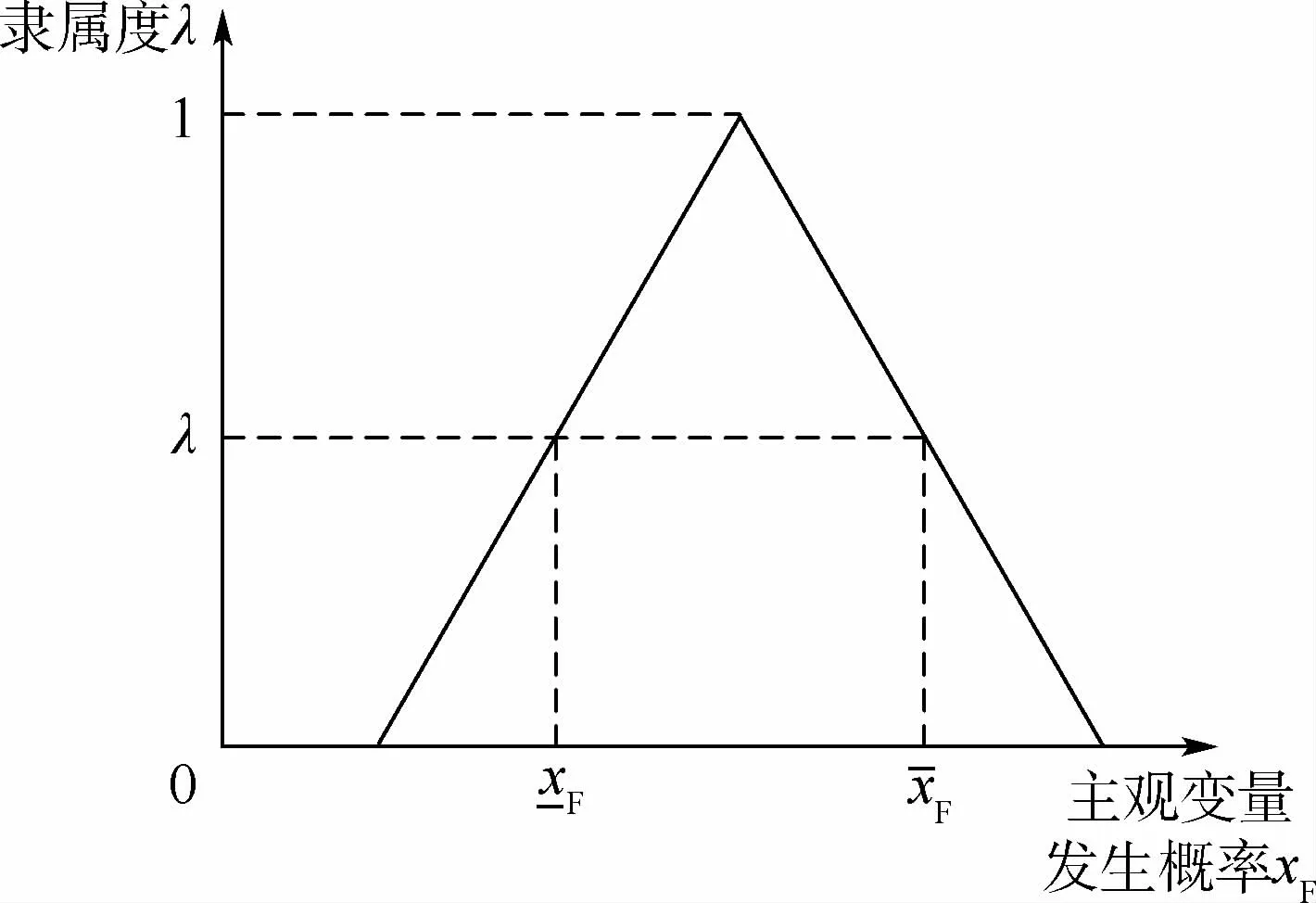
圖3 模糊變量λ水平截集描述Fig.3 Horizontal cut set description of fuzzy variableλ

2.3 基于信息更新的客觀不確定性變量動態更新

在保障仿真過程中，需要隨著實際工作展開，真實的參考數據不斷增加，其各類不確定性參數會隨時間發生變化，而采用基于信息更新的參數優化方法可以更準確地估計客觀不確定性變量的參數。因此，考慮將β的最大似然估計結果設為先驗分布，而后基于貝葉斯理論采用哈密頓蒙特卡羅方法［23］對β進一步優化，以解決傳統方法難以應對仿真模型變量描述無法動態更新問題。具體流程如圖4所示。

圖4 參數優化流程Fig.4 Parameter optimization flowchart

3 案例驗證

3.1 參數設置

以一個基本作戰單元3個月戰訓任務保障性仿真分析為例，先設定飛機初始狀態等固定參數值，采用基于統計數據的固定參數對不確定性變量進行描述，主要仿真參數如表2所示。

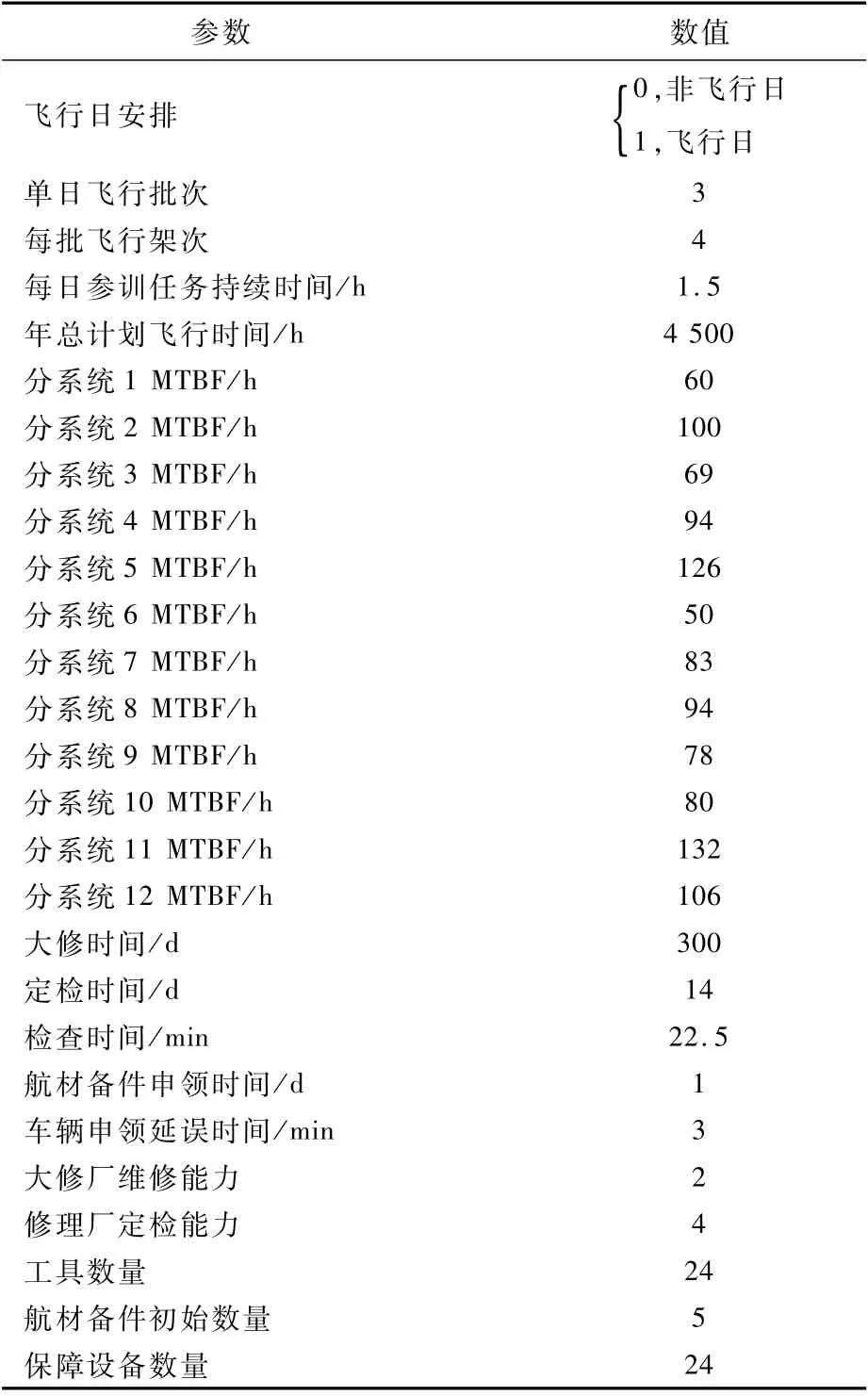
表2 主要仿真參數Table 2 Main simulation parameter s

利用前文處理方法對系統不確定性變量進行描述。對于客觀不確定性變量，通過統計各二級系統故障間隔時間，求解各二級系統故障率隨機分布參數結果，如表3所示。對大修時間、定檢時間、檢查時間等各主觀不確定性變量通過數據采集、調查問卷、專家打分等過程，利用采用三角模糊數［24］進行描述，結果如表4所示。

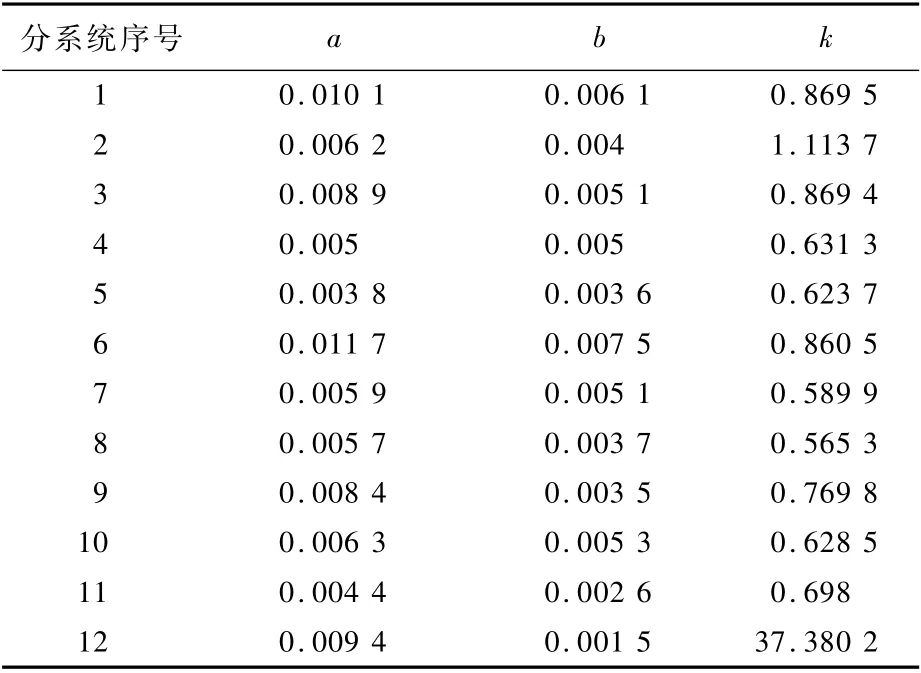
表3 客觀不確定變量分布參數Table 3 Objective uncertain variable distribution parameters

表4 主觀不確定變量分布參數Table 4 Subjective uncertain variable distribution parameters

為驗證考慮不確定性變量的仿真系統輸出結果對采用統計數據得到的確定性參數得到的輸出結果的分析補充作用，以參數設置為基礎進行基于固定參數的仿真結果分析和基于不確定性變量的仿真結果分析。

3.2 基于固定參數的仿真結果分析

以表2所得的基于統計數據所得的固定參數為輸入，運行仿真系統，可得仿真輸出的飛機完好率結果如圖5和圖6所示。

圖5中累計的飛機完好率變化幅度逐漸減小，且有穩定在0.89附近的趨勢，表現出飛機不完好狀態呈現規律性變化，因此累計的飛行完好率呈現趨于穩定的狀態；與此對應的是圖6中每天的飛機完好率后期穩定在0.79～0.92，表征隨著飛行任務的執行，完好飛機的數量在19～22架之間來回變化，呈現規律性變化。輸出結果表明，在該參數設置的保障形勢下可以穩定完成現階段保障任務。

圖5 累計的飛機完好率Fig.5 Cumulative aircraft readiness rate

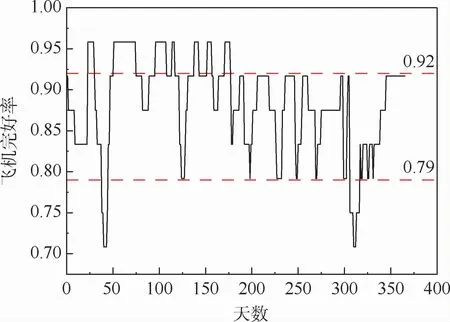
圖6 每天的飛機完好率Fig.6 Daily aircraft readiness rate

3.3 基于不確定性變量的仿真結果分析

通過3.2節得出，基于統計數據得到的固定參數下的仿真輸出可以在一定程度上有效評估保障模式，但無法評估不同保障形勢及各不確定性變量對裝備保障體系的具體影響。基于不確定性變量的仿真分析對此起到了補充作用。

以表3和表4的不確定性變量描述為基礎進行仿真參數設置，先為仿真不同保障形勢下基本作戰單元的飛機完好率，對上述不確定性變量參數進行同比放大或縮小，即將某些參數乘以一定的系數后輸入到仿真系統中，一方面為參數變量變更提供途徑，另一方面以不同參數值簡要表述不同程度不確定條件下飛機完好率指標變化情況，當參數設置為預定值時，參數放大系數為1.0，其他放大系數下仿真結果如圖7所示。

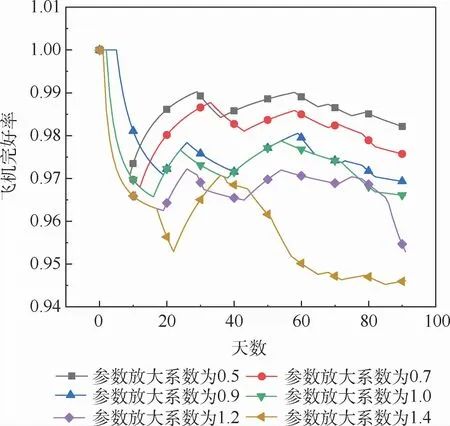
圖7 不同參數放大系數下飛機完好率指標變化Fig.7 Changes of aircraft readiness rate index under different parameter magnification factors

圖7反映了在不同參數放大系數下飛機完好率的變化情況。在參數放大系數為1.0的情況下，基本作戰單元執行完3個月戰訓任務后，飛機完好率為0.966 03，符合任務要求。其中隨著參數值的擴大，分系統故障平均間隔時間縮小，主觀不確定性變量數值增大，保障形勢惡化，飛機完好率整體呈下降趨勢；隨著參數值的縮小，保障形勢改善，飛機完好率呈現上升趨勢，仿真結果符合現實情況，進一步驗證了仿真系統評估的有效性和可靠性。

為考慮各不確定性變量對航空裝備體系輸出結果的影響，在驗證仿真系統有效性的基礎上，根據表3和表4對分別對所有不確定性變量、主觀、客觀不確定性變量進行隨機抽樣，進行1 000次3個月戰訓任務仿真實驗，仿真輸出的飛機完好率結果如圖8所示。

從圖8（a）中可以看出，所用案例考慮所有不確定性的仿真得出的基本作戰單元飛機完好率主要集中在0.15～0.5和0.9～1.0這9個區間，分別占比7.7%、7.9%、7.7%、5.3%、7.7%、4.5%、4%、15.7%、27.2%，而0.5～0.9內數據較少；分別對不同類別不確定性變量進行抽樣分析，圖8（b）反映了在客觀不確定性變量取平均值后，隨機抽取主觀變量得到的仿真結果，可以看出仿真結果均在0.9以上，且以0.96為中心呈類正態分布；圖8（c）反映了在客觀不確定性變量隨機抽樣后得到的結果，與考慮所有不確定性變量的結果基本一致。

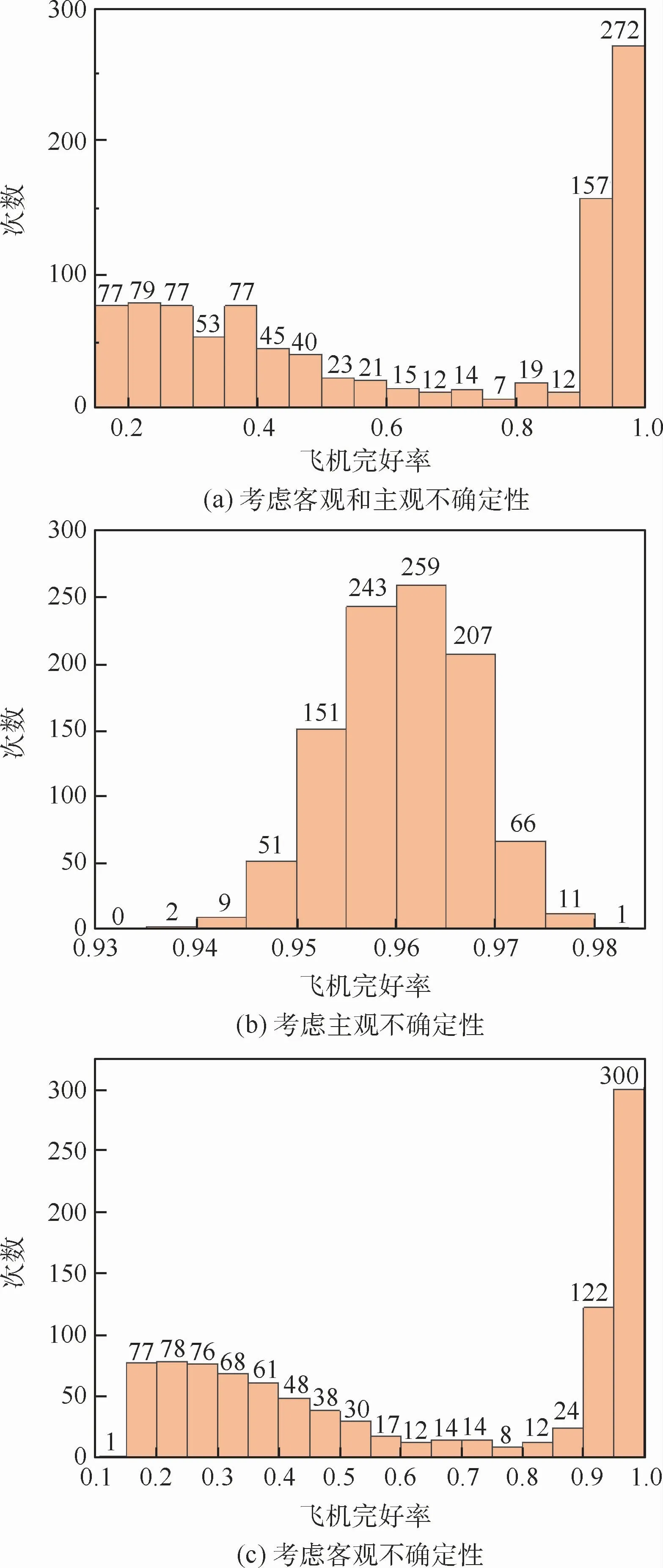
圖8 飛機完好率結果分布Fig.8 Results distribution of aircraft readiness rate

上述結果顯示，飛機完好率主要受飛機不完好架日的數量的影響，而任一不確定性變量的取值若不符合保障任務要求，均會導致飛機故障架日增加，若均符合保障要求，則飛機完好率會呈現較高水平。因此，在所有不確定性變量隨機取樣的情況下，仿真產生的飛機完好率結果呈現兩邊多中間少的結果。而由于主觀不確定性變量的描述多通過經驗及人為因素確定，取值范圍處于可完成任務的區間范圍內，在客觀不確定性變量取平均值，隨機抽取主觀不確定性變量的條件下進行仿真的結果均在0.9以上；同時因為采用三角模糊數對主觀不確定性變量進行描述，所以結果也呈現出兩邊少中間多的類正態分布。基于前述原因，可以分析得出在仿真過程中主觀不確定性變量對仿真結果輸出的影響主要起到閾值作用，只要在描述范圍之內就可以確保飛機完好率符合任務要求，而對仿真結果起重要影響因素的是客觀不確定性變量，其仿真結果同考慮所有不確定性變量的結果基本一致，因此在實際工作中重點關注客觀不確定性變量，使其符合保障任務要求，確保飛機完好率符合任務要求。

為了進一步驗證主觀不確定性變量的閾值作用，改變主觀不確定性變量定檢時間，其余參數保持不變，由此得到的飛機完好率結果如圖9所示。

由圖9可得，飛機完好率仿真結果同定檢時間成反比關系，且當定檢時間大于22 d時，飛機完好率小于0.80，表現出主觀不確定性變量的閾值作用，但由于在實際仿真中，主觀不確定性變量的確定往往根據往年數據將參數確定在合理區間內，因而在圖8所示的仿真結果中并不能明顯得到主觀不確定變量的閾值作用。

圖9 飛機完好率變化Fig.9 Changes of aircraft readiness rate

在策略控制上，為了有效確保完好率，一方面要加強設計制造研究，增大飛機分系統平均故障間隔時間，使其符合保障任務需求；另一方面優化調整保障工作流程，確保實際保障工作時間處于主觀不確定性變量的描述范圍內。

此外，為解決仿真時間偏長的問題，快速得到仿真結果，可采取代理模型來擬合仿真輸入輸出關系［25］。在代理模型中有很多方法可以使用，如多項式擬合［26］、擬合響應面法［27］、支持向量機［28］、神經網絡法［29］等。針對航空裝備體系保障流程，采用較簡單的多項式擬合的方法，通過隨機抽樣得出的仿真數據得到對應的不同階數的擬合多項式表達式，隨機抽取10組變量數據進行仿真實驗得到飛機完好率值，同時利用不同階數的快速響應仿真擬合表達式進行擬合計算，得到擬合飛機完好率，對比情況如圖10所示。

從圖10中可以看出，一階多項式擬合結果較好地表現了數據變化趨勢，但在數值的準確性上有所欠缺；二階多項式擬合結果在一階的基礎上對部分點的擬合結果有很大提升，但仍存在估值不準確的情況；三階多項式可以較好地擬合整個數據且未出現過擬合現象。因此，選擇三階擬合多項式表達式作為仿真系統的快速響應表達式，即在確定不確定性變量值后代入三階擬合多項式表達式中計算得到與仿真系統相似的結果。同時，針對一組數據，仿真輸出飛機完好率結果耗時3.3 s，而基于三階擬合多項式表達式的快速響應方法輸出飛機完好率僅需要0.1 s左右，在考慮不確定性條件下的仿真需要多次大量仿真結果的輸出，基于三階擬合多項式的快擬合方法縮短了分析時間，且給出了具體詳細的排序，增強了分析的針對性，為確定預防策略提供了精確方向。案例結果有效驗證了擬合方法的有效性，實現了仿真結果獲取的高效性。

4 結 論

1）對保障仿真模型中的客觀、主觀不確定性變量兩方面分別進行描述，完善了傳統航空裝備體系保障仿真模型中要素描述粗糙的不足，提高仿真系統準確性和有效性。

2）通過多項式擬合方法解決仿真系統運行時間較長、結果輸出慢的實際應用缺陷。

3）通過案例充分說明了提出的基于不確定性因素影響的航空裝備體系保障性仿真評估方法的可行性、完備性，以及對傳統仿真分析方法的補充作用，為快速評估保障系統保障性提供了思路。

本文在代理模型選擇上方法較為簡單，下一步將采用擬合效果更佳的代理模型來代替仿真過程，同時在主觀不確定性變量描述方面還需進一步探索和研究。