前體尾流對降落傘工作性能的影響

吳卓恒，余莉，2，*，趙曉舜，聶舜臣

（1.南京航空航天大學飛行器環境控制與生命保障工業和信息化部實驗室，南京 210016；2.南京航空航天大學航空學院，南京 210016）

降落傘由于其良好的減速性能和穩定性能，被廣泛用于各類飛行物體的減速回收。但是，在物傘系統的減速飛行過程中，降落傘均處于物體后面，前體尾流對降落傘的氣動性能有極其重要的影響。為了減小前體尾流對傘衣氣動性能的影響，在設計物傘系統結構時，通常需要將降落傘置于前體尾流區外。筆者將物傘的相對距離與前體直徑的比值稱為拖曳比。拖曳比過大雖然能克服尾流影響，但是會導致物傘系統質量增加、柔性加強、受環境影響加大。為了獲得合適的拖曳比，需要對前體尾流開展深入的研究。

前體尾流對降落傘工作性能的影響一直都是國內外物傘系統設計的研究重點。一部分學者通過風洞試驗開展研究，如Steinberg等［1］發現前體阻擋來流進入傘衣，隨速度增加前體尾流區范圍增大、動壓減小，傘衣阻力損失也會隨之增加。韓晉陽等［2］發現前置體的尾流效應會導致傘衣外形變化、傘衣收縮、投影直徑減小從而導致阻力系數減小。還有一部分學者通過數值模擬開展研究，主要有2種思路：一種是計算流體力學（Computational Fluid Dynamics，CFD）方法，該方法主要對物傘系統的流場分布規律及傘衣氣動特性進行研究，常用于傘衣外形變化不大的穩降階段，如Sengupta等［3-5］對超聲速降落傘進行CFD數值模擬，發現前體尾流改變了傘前激波形狀，進入傘衣內的氣流質量減少，傘衣阻力系數減小。賈賀等［6］發現傘前激波與前體亞音速尾流存在周期性的相互影響，在傘內高壓區的作用下傘前激波逐漸向前推進與前體激波相融合，而前體尾流又會導致傘前激波的擴散不穩定。另一種思路是流固耦合（Fluid-Structure Interaction，FSI）方法，該方法反映了非定常流場和柔性傘衣相互作用機制［7-10］，能直觀得到前體尾流對傘衣的氣動干擾情況，但數值模型復雜、耦合難度高和計算消耗大，通常用于外形變化比較劇烈的場合，如余莉和楊雪等［11-13］對超聲速盤縫帶傘進行了FSI數值研究，得到了以前體尾流和傘前激波為主的流場結構，分析了尾流作用下傘衣的激波振蕩和呼吸現象。Lingard和Xue等［14-17］對超聲速降落傘復雜的流場結構進行研究，發現前體尾流動壓減小會造成傘衣阻力損失，影響傘衣充氣過程的穩定性［15］，拖曳比過小前體尾流對傘衣氣動干擾強烈［16］，傘衣出現嚴重的收縮現象［17］。上述工作從不同角度均發現前體尾流對降落傘存在或多或少的影響，但是并沒有對前體尾渦結構及影響機制開展深入的研究。

本文基于Realizable k-ε湍流模型，采用PISO算法對穩降階段的物傘系統進行了非定常數值模擬，研究了不同拖曳比下前體尾流對流場分布和旋渦演變的非定常影響，分析了不同拖曳比下降落傘氣動特性的變化，為物傘系統的拖曳比設計提供一定參考。

1 數值計算方法

1.1 湍流模型及數值方法

在非定常計算中，湍流模型對流場結構（旋渦、壓力等）的捕捉和計算精度的影響很大，k-ε兩方程湍流模型被廣泛用于壁面繞流問題，其中Standard k-ε湍流模型考慮了速度和湍動能長度比例尺的分布，具備較好的計算精度和計算效率，但是忽略了氣流的黏性作用；Realizable k-ε模型增加了曲率和旋轉的影響，計算消耗增加但提高了計算精度。為獲得準確、精細的前體尾渦結構，本文基于Realizable k-ε湍流模型，采用標準壁面函數法（Standard Wall Functions）開展非定常繞流數值計算，湍流模型控制方程如下：

本文基于有限體積法采用MUSCL三階格式進行流場方程離散，為了提高瞬態計算精度并加速收斂過程采用PISO算法，其中壓力插值選擇Standard格式，為了能有效處理非定常計算的偽擴散問題選擇Green-Gauss Node-based進行梯度插值。邊界條件采用速度進口和壓力出口，采用了遠場邊界條件，傘衣面及前體為無滑移邊界條件。

1.2 方法驗證

為了驗證本文方法的有效性，采用文獻［18］中的平面圓形傘開展非定常數值計算。圖1為傘衣平面結構，當傘衣面積Ac＝40 m2、名義直徑D0＝7.1 m、傘頂孔直徑Dd＝0.4 m時，風洞試驗得到該傘的阻力系數為0.82。

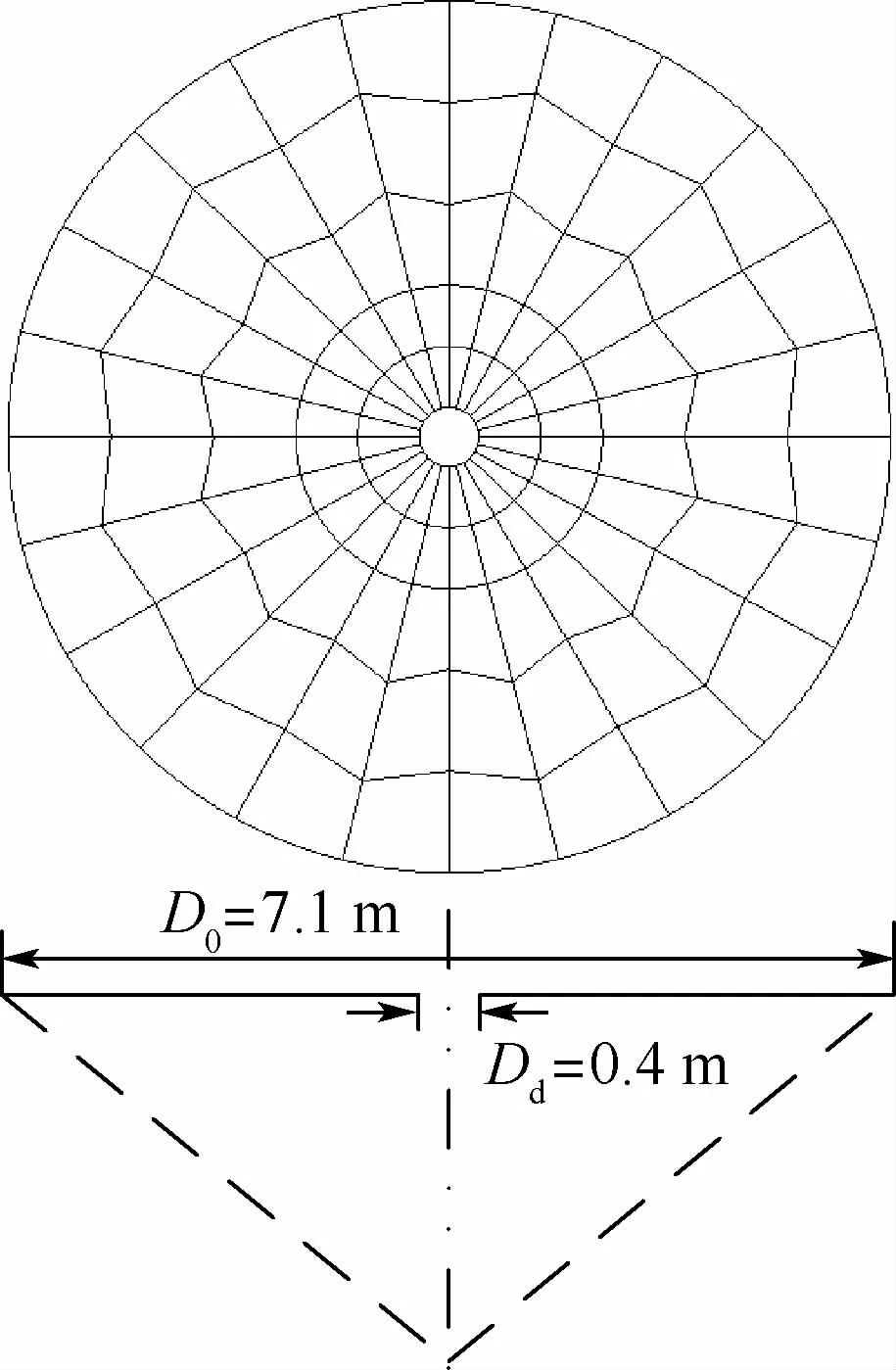
圖1 傘衣平面結構參數［18］Fig.1 Planar structure parameters of canopy［18］

本文針對降落傘穩降階段的非定常繞流流場展開數值研究，做如下假設：

1）不考慮前體和傘繩對流場的影響。

2）降落傘處于勻速穩定下降階段，傘衣外形不變，不考慮傘衣織物透氣性［19］。

3）傘衣充滿外形為半球形，投影直徑Dt和名義直徑D0的比取經驗值0.7［20］。

4）流場計算域為圍繞傘衣軸對稱的圓柱形，計算域直徑為6 Dt、高為8.6 Dt。

根據上述假設，本文建立如圖2所示的傘衣充滿外形和流場網格模型，D、hj分別為傘衣充滿下的傘頂孔直徑、傘衣高度，其中，在傘衣附近及尾渦區進行了網格局部加密，以增加計算精度和捕捉尾渦細節，網格總數為121萬。計算工況為：計算高度為H＝400 m，來流速度v＝15 m/s，大氣壓力p0＝95 kPa。

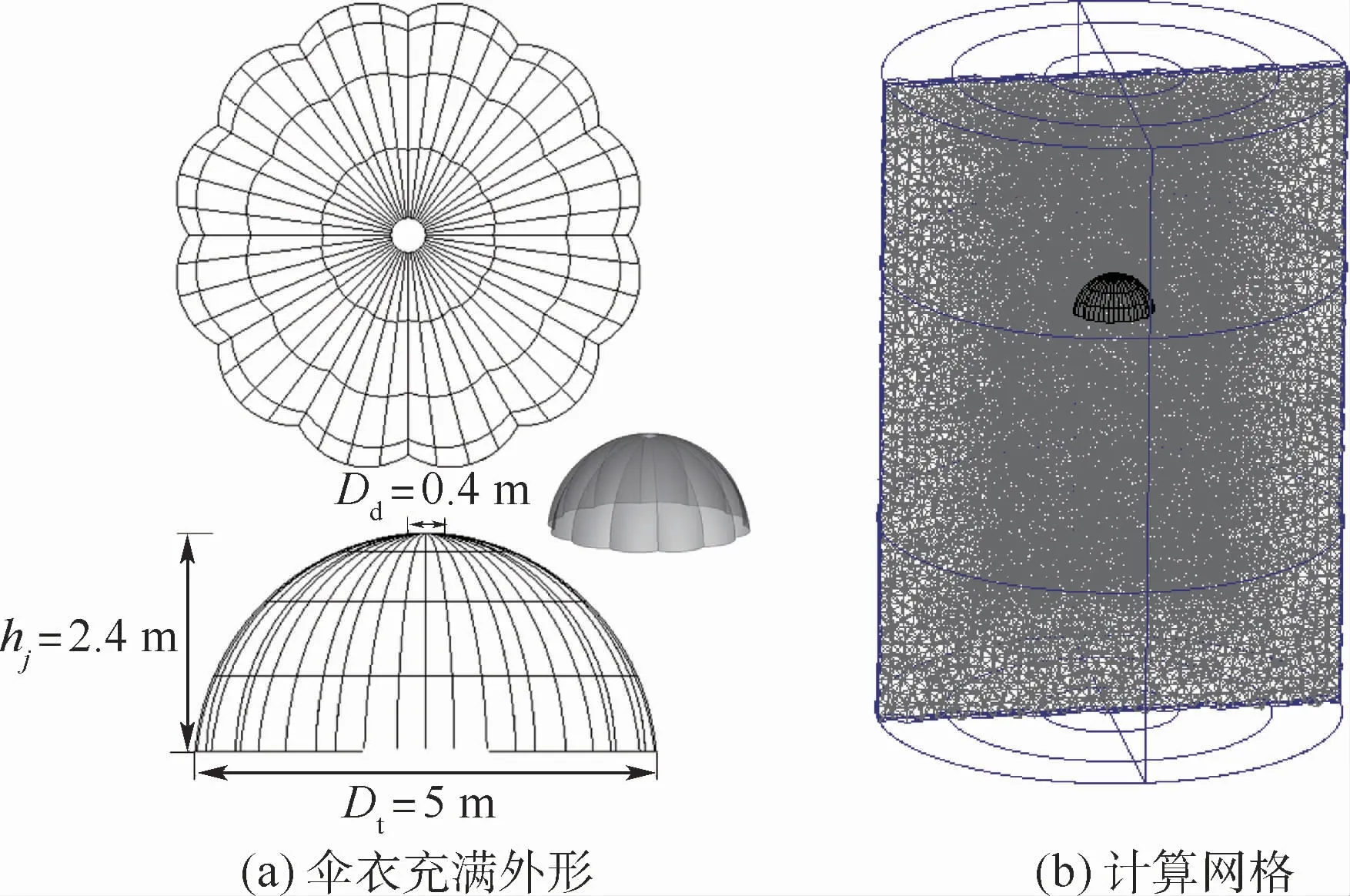
圖2 傘衣充滿外形和計算網格Fig.2 Full shape of canopy and computational grid

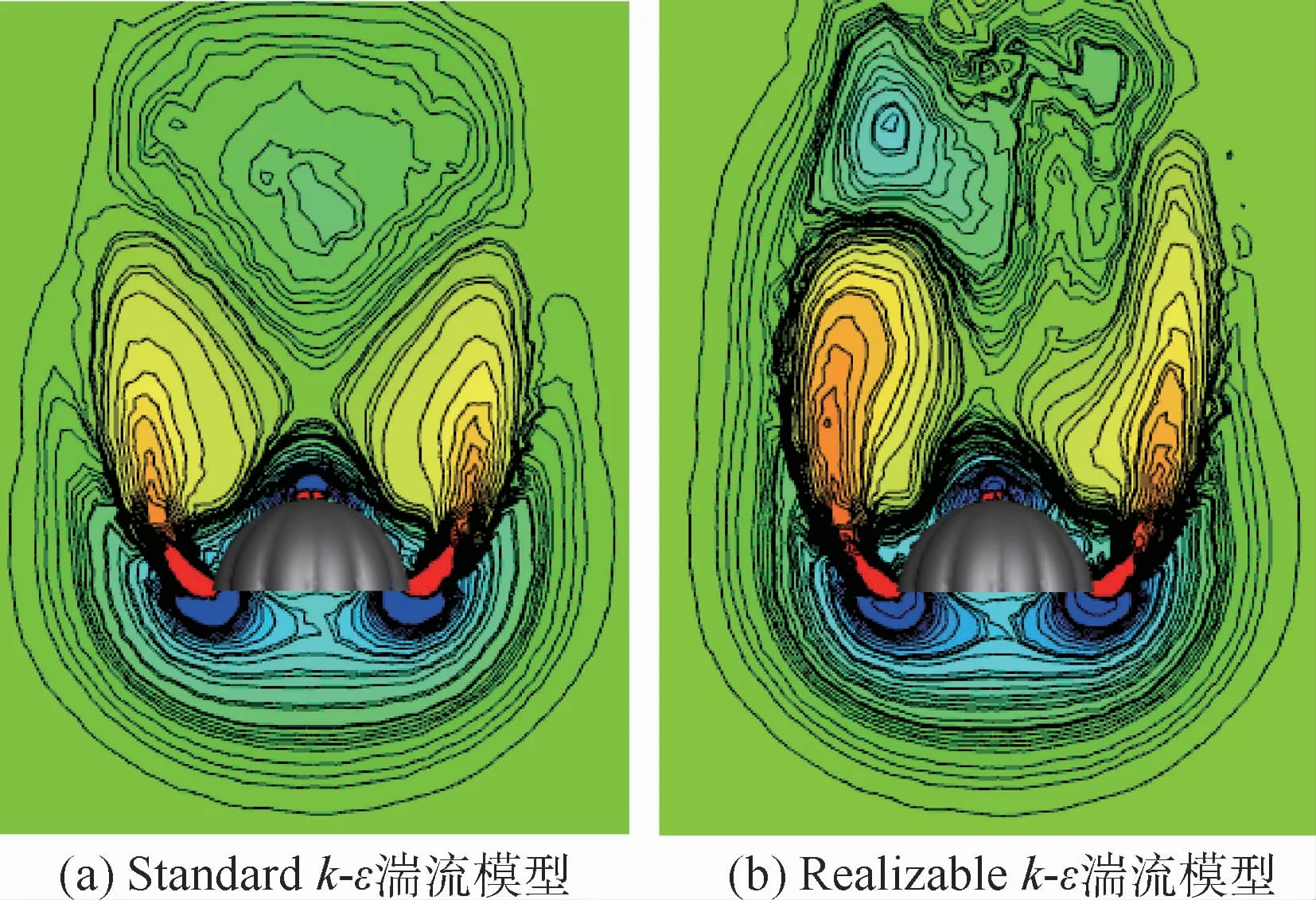
圖3 降落傘尾渦結構Fig.3 Parachute wake vortex structure

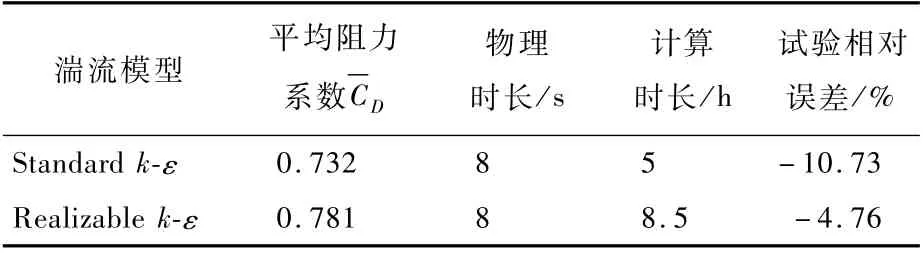
表1 數值計算結果Table 1 Numerical calculation results

2 研究對象及工況

本文針對1.2節的降落傘加附圓錐形前體，開展不同拖曳比下物傘系統的繞流流場計算，物傘系統三維模型如圖4所示。前體直徑d＝2.4 m、高h＝2.5 m；α為前體錐角；拖曳比λ分別取2、4、6、9、12；大氣條件為離地高度H＝200 m，來流速度v＝15 m/s。

圖4 物傘系統三維模型Fig.4 3-D model of capsule-parachute system

非定常固壁繞流問題中，網格對流場結構影響很大，為獲得準確的尾渦結構變化，本文采用求解固壁繞流適應性好的三角形網格，同時對尾渦區的流場網格進行加密，物傘網格數為11 631個，流場網格數為143萬個，數值模型如圖5所示。

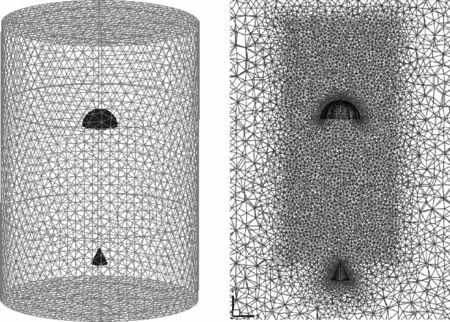
圖5 物傘系統數值模型Fig.5 Numerical model of capsule-parachute system

3 計算結果及分析

3.1 旋渦演變分析

圖6為計算穩定之后的流場旋渦分布。可以看出，在穩降階段，前體和傘衣表面仍不斷出現旋渦的生成與脫離，當λ≤6時，傘衣受前體尾渦影響嚴重，傘衣入口的渦量大小和方向時刻發生變化，這可能是造成傘衣擺動的重要原因；隨著拖曳比增加，前體尾渦的黏性耗散增加、渦量逐漸減少，當λ≥9時，傘衣入口開始形成穩定的負渦量區，物傘系統的繞流流場相對穩定，前體尾渦對傘衣的影響逐漸減弱。

圖6 流場旋渦演變規律Fig.6 Variation rule of flow field vortex

3.2 流場分布規律

圖7 物傘尾渦脫離周期和平均渦核渦量Fig.7 Wake vortex departure period and average vorticity magnitude of capsule-parachute system

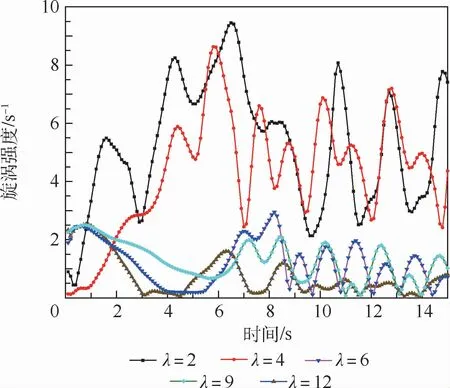
圖8 傘衣入口處旋渦強度變化Fig.8 Variation of vorticity magnitude at the entrance of canopy

圖9為不同拖曳比下趨于穩定時物傘系統的流場分布。可以看出，拖曳比改變著物傘系統的繞流流場分布，當拖曳比過小時（如λ＝2），前體阻擋了自由來流進入傘衣，前體和傘衣形成閉式流動，流域P氣流動壓極低，傘衣阻力損失嚴重；隨著拖曳比增加逐漸轉變為開式流動，前體尾流區的壓力和氣流速度具備恢復的過程，物傘系統的流場速度分布和壓力分布更為對稱，傘衣底部形成穩定的正壓區。

圖9 物傘系統流場圖（t＝15 s）Fig.9 Flow field of capsule-parachute system（t＝15 s）

為探究拖曳比對前體和傘衣附近流場影響的強弱，在對稱軸前體后方0.5 m處（A點）和傘衣入口前方0.5 m處（B點）進行流場壓力監測，得到2個特征點的壓力變化情況（見圖10）。從圖中可以看出，穩定后前體尾流區前端（A點）的壓力變化幅度遠小于后端（B點），拖曳比對后端（B點）流場壓力的影響遠大于前端（A點）。隨拖曳比增加，A點的流場壓力逐漸減小，而傘衣入口B點的流場壓力明顯增大。當λ＝2時，傘衣入口和前體后方流場壓力的變化趨勢和大小幾乎一致，此時傘衣位于前體尾流負壓區內，傘衣完全處于閉式流動中。

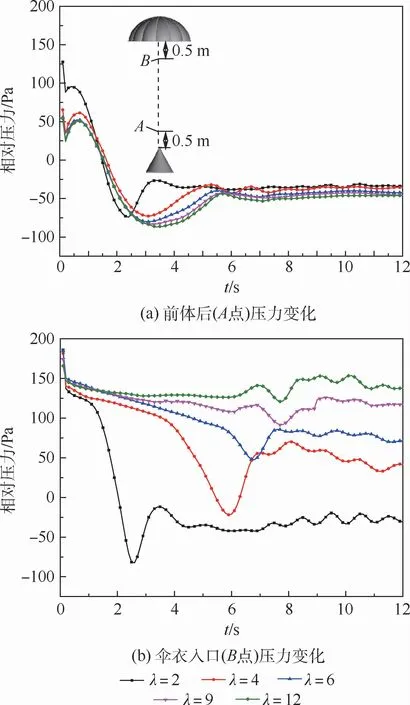
圖10 流場壓力變化Fig.10 Variation of flow field pressure

3.3 氣動特性分析

圖11為不同拖曳比下傘衣沿子午線上的內外壓力及壓強系數Cp分布。可以看出，傘衣完全處于閉式流動時（λ＝2），傘衣內外側壓力大小接近，壓強系數較小且存在負值的情況，降落傘正常的工作性能受到影響；而當傘衣處于開式流動時（λ≥2），傘衣內側壓力均明顯大于外側壓力，具有較好的減速能力，隨著拖曳比增加，傘衣內外側壓力和壓強系數均逐漸增加，氣動阻力增加；當λ≥9時，尾流對傘衣面壓強系數的影響減小。

圖11 傘衣沿子午線上的內外壓力及壓強系數分布Fig.11 Internal and external pressure and pressure intensity coefficient distribution along the meridian of canopy

圖13 平均阻力系數隨拖曳比的變化Fig.13 Variation of average drag coefficient with drag ratio

4 結 論

為研究前體尾流對降落傘工作性能的非定常影響，本文開展了不同拖曳比下物傘系統的數值研究，得出如下結論：

1）拖曳比對前體尾渦脫離周期幾乎沒有影響，但對傘衣影響很大。隨拖曳比增加，前體尾渦到達傘衣入口處的時間增加，受渦量黏性耗散影響，進入傘衣的旋渦強度減弱，傘衣底部形成穩定負渦量區，傘衣尾渦脫離周期隨之延長。

2）當拖曳比過小時，傘衣完全處于尾流區內，形成閉式流動。隨著拖曳比增加逐漸轉變為開式流動，物傘系統的流場速度和壓力分布更為對稱，傘衣底部形成穩定的正壓區。

3）拖曳比對傘衣入口處流場壓力的影響遠大于前體后方。隨拖曳比增加，穩定時的流場壓力明顯增加，傘衣內外壓差增加，但當λ≥9時，前體尾流對降落傘阻力系數和傘衣面壓強系數的影響減小。