基于帕德逼近響應面法的邊坡可靠度分析

梁 斌，高樂星，何 杰，吳 政，劉 杰

（湖南工業大學 土木工程學院，湖南 株洲 412007）

崩塌、泥石流、滑坡等邊坡災害會危害人們的生命及財產安全，因此，進行邊坡穩定性分析和評估相當重要。由于邊坡工程的破壞模式和巖土參數都存在不確定性和變異性，故常運用可靠度分析方法來評價邊坡的穩定性，該方法已得到了廣泛認可。常見的可靠度分析方法有直接積分法、矩分析法、響應面法、Monte-Carlo 法等[1-2]。直接積分法是可靠度分析中最基礎的計算方法，但當計算結構失效概率時，其在實際工程應用中將遇到極大障礙。矩分析法在進行可靠指標求解時，通常需求解功能函數對基本變量的導數，這對高度非線性隱式函數來說非常困難。Monte-Carlo 法雖然能得到精確解，但計算量巨大，收斂速度較慢。響應面法的適用性較強，但是當功能函數的非線性程度較高時，使用傳統的響應面法可能會出現精度及效率低的問題。因此，本文擬基于帕德逼近有理多項式提出一種新的代理模型響應面方法（response surface method based on Pade approximation，PRSM）。首先，采用拉丁超立方試驗構造樣本，并將樣本數據代入簡化Bishop 算法中，得到邊坡功能函數值；然后，通過求解得到代理模型的待定系數，從而實現隱式功能函數顯式化；最后，通過兩個經典的邊坡算例，驗證該方法的可行性、計算的高效性及準確性，為邊坡工程高度非線性隱式功能函數的可靠度求解提供一條切實可行的途徑。

1 邊坡穩定性分析功能函數

1.1 極限平衡法理論

極限平衡法、極限分析法以及滑移現場法[3]等都是常用的邊坡穩定分析方法。目前國內外普遍使用的分析方法為極限平衡法。它以摩爾-庫侖強度準則為基礎，通過計算邊坡已知滑移面的靜力平衡，最終得到邊坡穩定安全系數，以此評價邊坡的穩定性。極限平衡法不僅邏輯嚴謹而且簡單適用，至今已形成多種計算方法，如Bishop 法、簡布法、摩根斯坦-普瑞斯法、薩爾瑪法[3]等。極限平衡法的計算結果精度很高，能滿足工程要求。所以，在諸多邊坡穩定性分析方法中，極限平衡法的地位相當重要。

1.2 簡化Bishop 法

目前，極限平衡法中的瑞典圓弧法（Fellennius法）和簡化Bishop 法仍為邊坡工程中兩種常用的穩定性分析方法。相較于用瑞典圓弧法計算得到明顯偏低的安全系數Fs，經過優化土條間作用力假設的簡化Bishop 法更為合理，計算更簡單。因此，本研究將采用極限平衡法中的簡化Bishop 法建立邊坡的穩定性功能函數。簡化的Bishop 法大大改進了傳統的瑞典圓弧方法[4]，除了給出安全系數Fs的定義之外，還忽略了條間剪力，并假定土條之間的力是水平的，則土條底面上的法向力由在豎直方向上的靜力平衡條件求出。Fs借助邊坡整體力矩平衡方程來確定。

簡化Bishop 法中，滑體被劃分為n個豎直條塊，滑體及條塊間作用力如圖1所示。計算參數如下：R為滑面半徑，Wi、bi、αi分別為第i個條塊的重力、寬度、網弧底面傾角，ui、Ni、Ti分別為第i個條塊的孔隙水壓力、法向作用力、圓弧底面剪力，Ei、Ei+1、Xi、Xi+1分別為第i個與第i+1 個條塊的橫向作用力和縱向作用力，ci為黏聚力，φi為滑面內摩擦角。

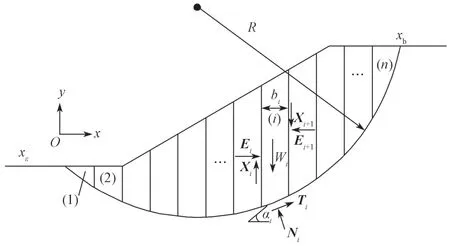
圖1 滑體及條塊間作用力示意圖Fig.1 Schematic diagram of the force between the sliding body and the bars

由太沙基有效應力原理和摩爾-庫侖準則可得：

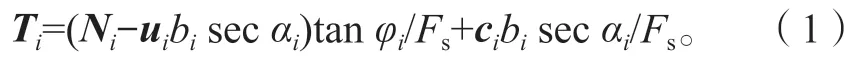
豎直方向上條塊間力的平衡方程如下：

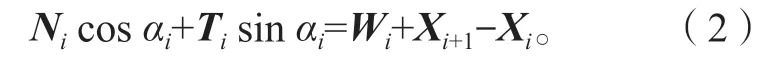
由式（1）和（2）可得：

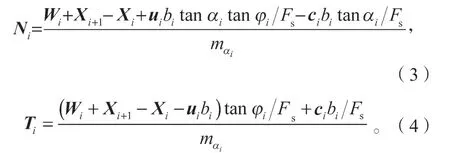
式（3）（4）中：

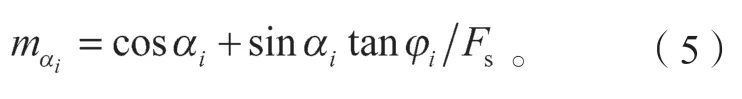
僅考慮對圓心的力矩平衡，不考慮滑體條塊水平方向力的平衡，則有：

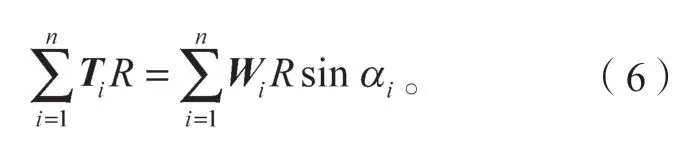
將式（3）（4）代入式（6），得

忽略滑體條間剪力作用，則簡化Bishop 法的安全系數Fs[5]的表達式如下：

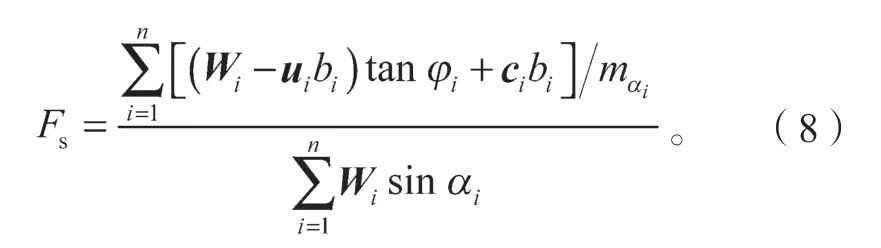
建立邊坡穩定性功能函數[6-7]，即

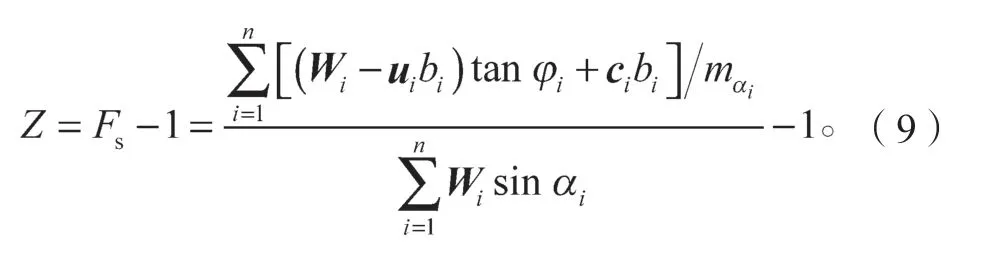
由式（8）（5）可知，Fs為隱式函數，同時也是關于ci、φi、Wi的函數，所以式（9）表示的邊坡功能函數屬于高度非線性隱式函數，此時采用傳統的可靠度計算方法，如直接積分法，將會遇到極大困難。

2 基于帕德逼近的響應面法

2.1 抽樣方法

邊坡穩定性分析中，許多參數都存在隨機性和變異性，故變量的樣本數據選取需要采取試驗設計抽樣方法來實現，因為試驗要想獲得所有的參數樣本非常困難。蒙特卡洛抽樣、正交試驗設計和拉丁超立方抽樣都是常見的抽樣方法。樣本點的選擇不僅要反映基本參數與功能函數之間的映射關系，還必須最大程度地代表整個變量空間的性質，并且試驗次數還要盡量小。作為一種分層隨機抽樣方法，拉丁超立方抽樣方法可用較少數量的樣本反映總體的變化趨勢，避免了重復抽樣，有效減少了抽樣次數。因此，本文參數樣本的選取采用拉丁超立方抽樣完成。

從理論上分析，樣本點越多，計算結果精度越高，功能函數的模型代理表達式越精確，但相應的計算代價越大。根據目前已有研究成果[8]得知，模擬時一般選取30 組樣本較為合適。

2.2 帕德逼近

帕德逼近是由法國數學家亨利·帕德發明的，它是一種非線性逼近方法，也是有理函數逼近中比較特殊的一種方法。與截斷的泰勒級數相比，帕德逼近通常更加精確，并且帕德逼近在泰勒級數不收斂的情況下依舊可行，所以其在許多物理問題上甚至實際問題中都有較為普遍的應用。假設一個分式，它的分子為多項式，分母也為多項式，就等于一個無窮級數，如1/(1-x)=1+x+x2+···+xn+o(xn)，帕德逼近就是找到無窮項中收斂較慢的級數，然后將其變成有限多項式除法運算。以泰勒級數多項式為基礎，帕德逼近構造了一類近似的有理多項式函數以替代原函數的方法。函數f(x)的有理逼近可通過其泰勒展開式獲得[9]。

設f(x)∈CN+1(-a,a)，若有理函數

（式中Pn(x)與Qm(x)無公因式）滿足：

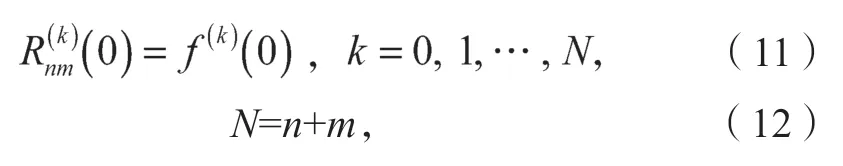
則將Rnm(x)稱為函數f(x)在x=0 處的(n,m)階帕德逼近，表示為R(n,m)。

由此可得如下逼近公式：

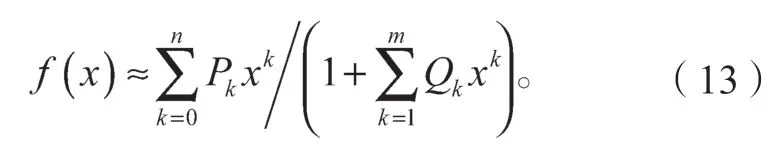
大量研究結果[10-11]顯示，當n=m，且n+m為常數時，帕德逼近具有最佳精度和最快收斂速度。

2.3 邊坡功能函數模型代理

邊坡的功能函數為一個高度非線性的隱式函數，首先考慮將其顯式化后再進行可靠度計算，依據帕德逼近方法，可取如式（13）所示的功能函數近似顯式表達式，其中n=m，邊坡的各參數如ci、φi、γi（容重）可視為隨機向量x=[x1,x2,…,xj]，可得近似的邊坡功能函數Z的表達式為

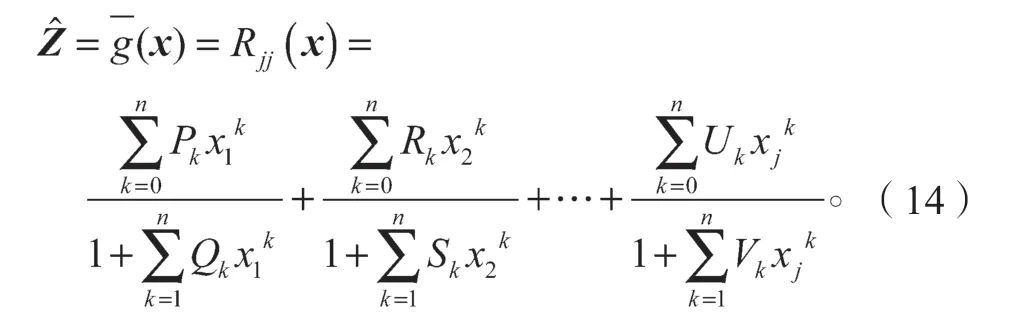
式（14）即為邊坡PRSM 代理模型。

然后，將邊坡參數訓練樣本X=[x(1),x(2),…,x(m)]，容量為m，代入簡化Bishop 功能函數式（9），經迭代后獲得樣本的真實響應值Y=Z=[Z(1),Z(2),…,Z(m)]；再將X、Y代入PRSM 代理模型式（14），求得Pk、Qk等待定系數，最后獲得清晰的PRSM 邊坡功能函數表達式。

2.4 可靠度計算步驟

利用PRSM 模型代理邊坡的功能函數后，選取可靠度分析方法來計算可靠度與失效概率，本研究采用一次二階矩法中的JC 法[1-2]編制Matlab 程序進行可靠度計算。

3 代理模型方法精度驗證

3.1 實例1

一均質邊坡[12]，其橫截面如圖2所示，高H=20 m，坡比為1∶1，其土層參數如下：泊松比v=0.3，彈性模量E=20 MPa，內摩擦角φ=20o，黏聚力c=40 kPa，剪脹角ψ=20o，容重γ=20 kN/m3。c、φ相互獨立，均服從正態分布，變異系數都為0.1。

圖2 實例1 邊坡橫截面示意圖Fig.2 Schematic diagram of the slope cross section in example 1

邊坡上部邊界自由，底部邊界為剛接，兩側為水平滑動支承，同時視邊坡土體為摩爾-庫侖理想彈塑性模型。上述土層參數中，容重γ變異較小，變異性相對較大的為內摩擦角φ和黏聚力c。因此容重γ的變異性不納入考慮范圍，視為定量參數進行分析，把c、φ視為隨機參數。將其表示為隨機向量x={c,φ}={x1,x2}的形式。通過拉丁超立方試驗設計抽樣得到30 組樣本后，再由簡化Bishop 法獲取相應的功能函數值，其計算結果如表1所示。

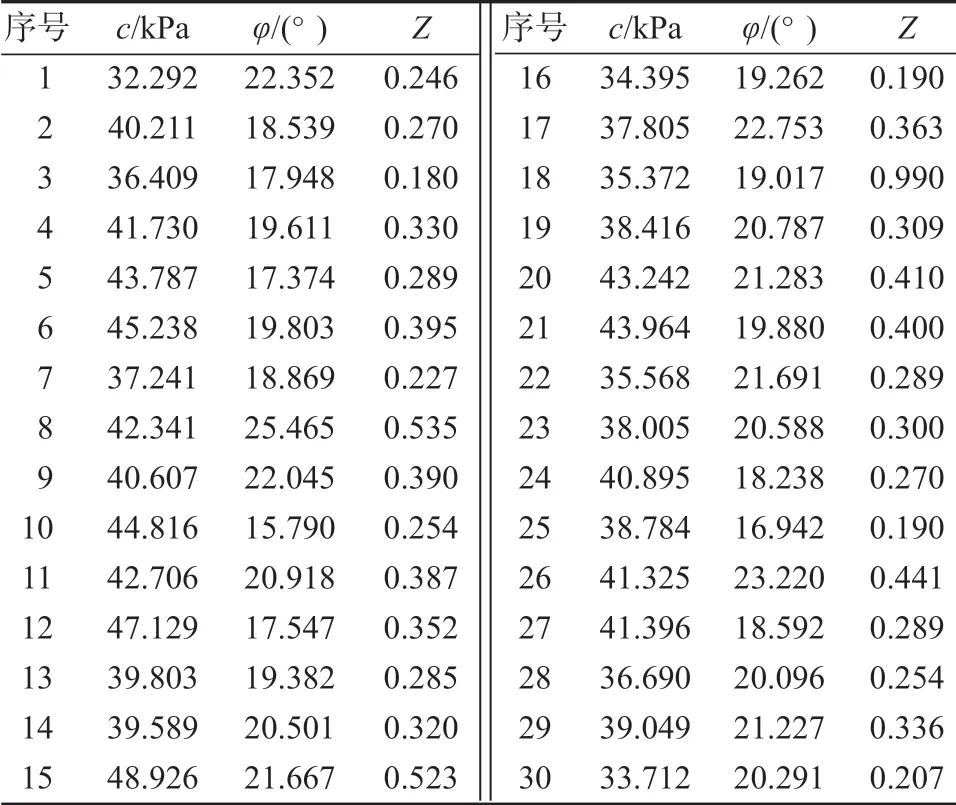
表1 實例1 樣本點及功能函數計算結果Table 1 Calculation results of sample points and function functions in example 1

在獲得表1中的30 組數據和其相應的功能函數值之后，根據式（14）可求得其中的有理多項式系數Pk、Qk、Rk、Sk、Uk、Vk，從而構建了PRSM 邊坡代理模型。然后，采用JC 法進行計算，選取均值點(40,20)作為驗算點初值。取(1,1)階帕德逼近響應面代理模型，經迭代后，求得可靠度指標β(1,1)=3.151 8，相應的失效概率Pf=8.114 1×10-4。取(2,2)階帕德逼近響應面代理模型，求得可靠度指標β(2,2)=3.294 4，相應的失效概率Pf=4.931 5×10-4。

在文獻[13]中，結合ANSYS 和響應面法所求解的可靠度為β=3.420，Monte-Carlo 法求解的可靠度為β=3.234，驗算點法求解的可靠度為β=3.215，傳統響應面法求解的可靠度為β=3.214。本文方法的計算結果與上述結果均相差很小，證明了本文方法是可行的。并且對比Monte-Carlo法求得的可靠度指標3.234，文獻[13]中的方法誤差為5.75%，本研究所用方法的誤差僅為1.87%，可見本研究提出的方法擁有更高的精確度。在文獻[13]中，ANSYS 的求解原理為強度折減，且程序一次只能求解一個結果，非常繁瑣、緩慢。再者有理多項式的擬合精度比二次多項式的明顯要高。在進行可靠度分析時，尤其是當隨機變量的數量增加時，采用基于帕德逼近的響應面方法在效率與精度方面均優于上述其他方法。

3.2 實例2

圖3為一雙層邊坡[14]，高15.24 m，坡比為1∶2。其土層參數如下：彈性模量E=100 MPa，泊松比v=0.3，黏聚力c1=38.31 kPa，c2=23.94 kPa，內摩擦角φ1=0o，φ2=12o，容重γ=20 kN/m3。c1、c2、φ2是互為獨立的正態隨機變量，變異系數分別為0.2,0.2,0.1，其余參數為定值。

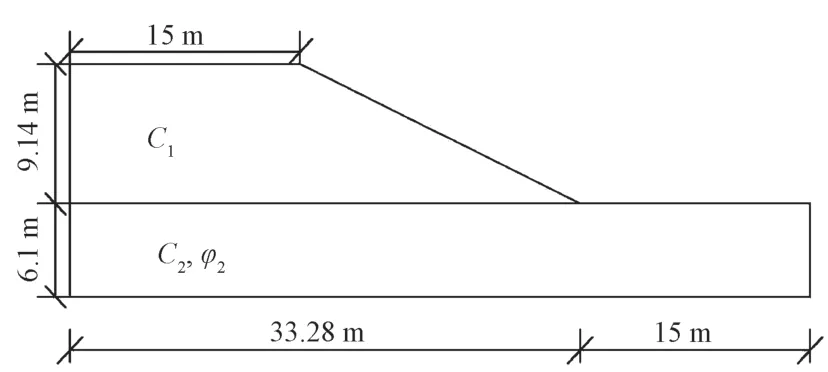
圖3 實例2 邊坡橫截面示意圖Fig.3 Schematic diagram of the slope cross section in example 2

以上土層參數中，把c1、c2、φ2作為隨機參數。同樣30 組樣本通過拉丁超立方抽樣生成后，再由簡化Bishop 法獲取相應的功能函數值，其計算結果如表2所示。然后利用本文所提出的方法，分別采用基于(1,1)階和(2,2)階帕德逼近有理多項式的響應面方法進行邊坡可靠度分析，所得計算結果見表3。

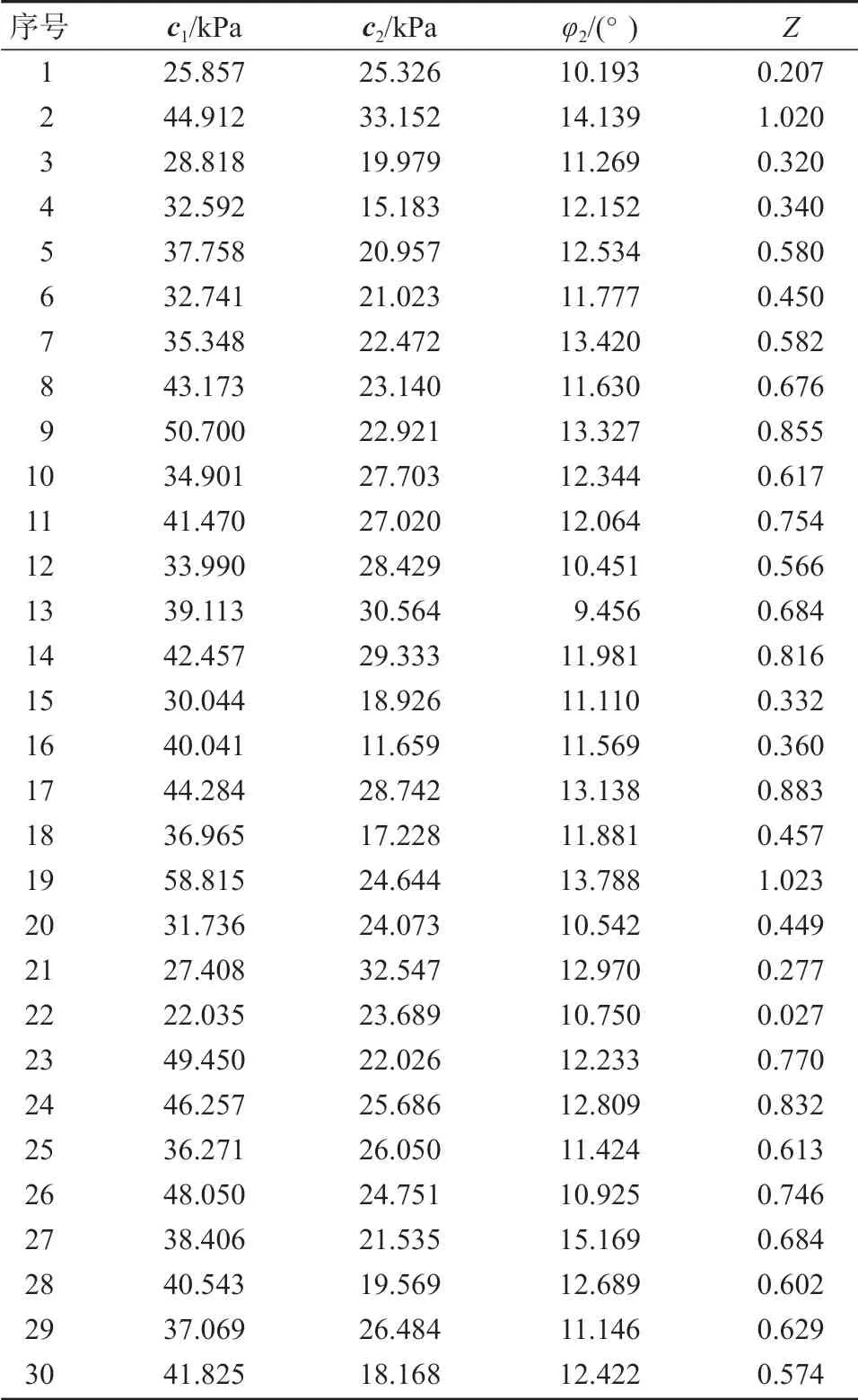
表2 實例2 樣本點及功能函數計算結果Table 2 Example 2 sample points and function function calculation results

將表3中的數據與文獻[14]和文獻[15]中所計算的結果進行比較，可以發現可靠度指標結果比較接近，因而進一步證實了本文方法的可行性。但是本實例中，(1,1)階PRSM 方法比(2,2)階PRSM 方法的計算精確度更高。其原因可能是：當隨機變量數量增加時，拉丁超立方抽樣方法抽取的基本隨機變量樣本數量過少，在擬合PRSM 代理模型的多項式系數時沒有取到最優值。

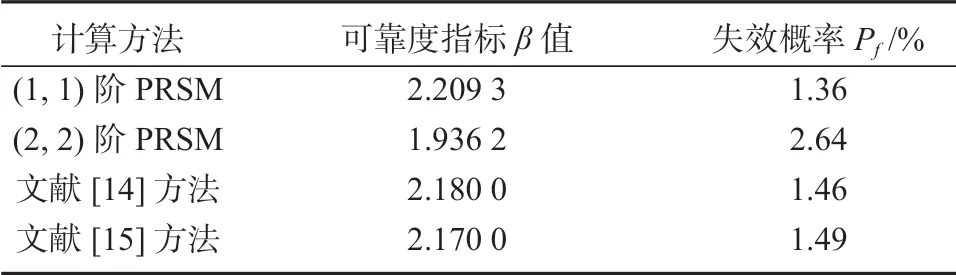
表3 不同計算方法的可靠度結果Table 3 Reliability results calculated by different methods

4 工程實例分析

某高速段路塹邊坡坡高約為15 m，坡比為1:2。層狀構造，巖體主要是炭質砂巖。邊坡上部地層為紅褐色粉質黏土，硬塑性，厚為0～1 m；中部地層為灰色弱風化碳質砂巖，厚度大于3 m；下部地層為青灰色全風化碳質砂巖，厚度大于10 m。進行土工試驗后得知，該路段各地層容重γ變異較小，黏聚力c、內摩擦角φ的變異性較大，所以把c、φ作為隨機參數，不考慮γ的影響。該工程實例的地層力學參數和統計特征如表4所示。

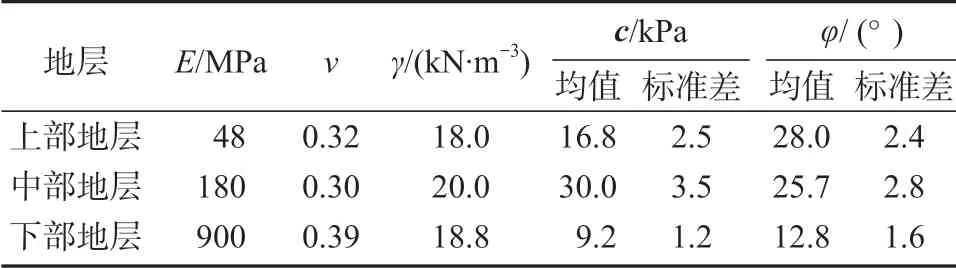
表4 工程實例地層力學參數及統計特征Table 4 Ground mechanics parameters with the statistical characteristics of engineering examples

把上部地層、中部地層、下部地層的物理力學參數c1、φ1、c2、φ2、c3、φ3寫成隨機向量的形式x={c1,φ1,c2,φ2,c3,φ3}={x1,x2,x3,x4,x5,x6}，所得計算結果如表5所示。

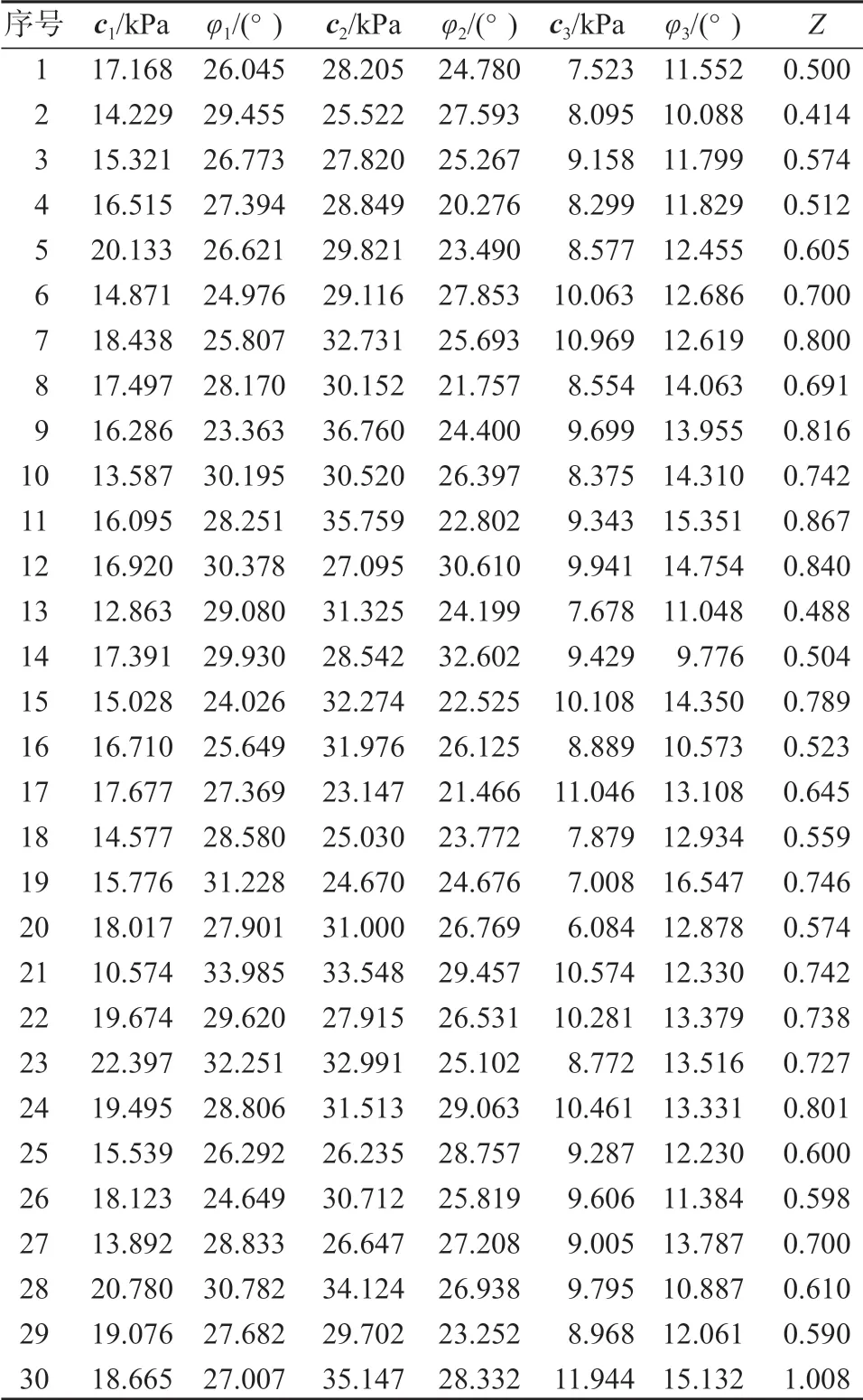
表5 工程實例樣本點及功能函數計算結果Table 5 Project example sample points and function function calculation results

根據表5中的30 組樣本和其功能函數值構建基于帕德逼近有理多項式的邊坡功能函數的響應面模型；再利用JC 法，經計算，得到β=5.024 2，Pf= 2.528 1×10-7。計算結果表明，該路塹邊坡出現失穩狀況的可能性較低。

5 結論

1）本文采用極限平衡法中的簡化Bishop 法，利用拉丁超立方試驗設計構造樣本，構建了基于帕德逼近有理多項式代理模型的邊坡可靠度計算方法（PRSM），為邊坡工程高度非線性隱式功能函數可靠度求解提供了一條新的途徑。

2）PRSM 法針對傳統響應面方法中的響應面函數進行改進，用基于帕德逼近有理多項式的形式替代傳統的二次多項式形式，其計算結果精度更高，且當隨機變量增加時，(2,2)階PRSM 的精度比(1,1)階PRSM 的更高。但也會出現(2,2)階PRSM 的精度不及(1,1)階PRSM 的情況，推測其原因為抽取的基本隨機變量樣本數量過少或沒有在擬合PRSM 代理模型的多項式系數時取到最優值等，有待進一步研究。

3）通過實例驗證，表明本文方法是可行的，且當計算精度接近時，其工作量小于蒙特卡洛法，具有一定的工程實用性。