基于影響矩陣法的鋼管混凝土拱橋索力優化模型

鄧宗仁，何楚韶，劉運思，杜憲武，楊玉平

（1.中鐵北京局集團（天津）工程有限公司，天津 300000；2.湖南科技大學 巖土工程穩定控制與健康監測省重點實驗室，湖南 湘潭 411201）

0 引言

鋼管混凝土拱橋在拱肋中充填混凝土，可充分發揮混凝土的強度及提高其變形性能，同時也可以增強拱橋整體的穩定性。此外，鋼管拱肋采用分節吊裝拼接而成，能極大地縮短工期，同時也節省了混凝土澆筑模板的費用，使其在跨越50～200 m 的地形障礙時相較其他類型的橋梁具有明顯的優越性。

系桿拱橋的施工中，張拉吊桿是十分關鍵的一環。吊桿的張拉一般分幾個批次進行，后期的張拉會對前期的張拉效果產生影響，從而導致部分吊桿的受力不在控制范圍內，這就會造成工期后延，成本增加。因此，如何確定合理的張拉力、張拉順序，減少張拉的次數成為吊桿領域的研究熱點。近年來，研究人員對這一領域進行了深入研究，成果頗豐。王祥國等[1]為優化吊桿張拉次數，結合影響矩陣法[2-3]，對吊桿的張拉模型進行了優化，并通過算例驗證了模型的可靠性。任亮等[4]采用恒載“零彎矩”法計算拉索索力，并以優化恒載彎矩的分布為目標，對拉索索力進行了優化。何畏等[5]運用Ansys 對上承式拱橋進行了建模，通過調整最大懸臂狀態下扣索索力來優化拱圈的應力。徐岳等[6]在影響矩陣法的基礎上，結合正裝差值迭代法來確定最佳的扣索索力。張治成等[7]以大跨度橋為例，引入最優化計算理論，并結合有限元模擬，有效解決了線性調整中的索力計算問題。胡常福等[8]提出了基于均勻設計影響面結合牛頓迭代的非線性索力優化方法，該方法運行效率較高，可有效減少計算時間，在新型索拱橋的索力優化中具有良好的適用性。傅金龍等[9]比較了幾種索力優化方法及其適用性，并結合具體的工程實例進行了驗證。

在上述研究的基礎上，本文以東海特大系桿拱橋為例，基于影響矩陣法，構建了索力優化模型，以優化吊桿張拉次數為目標、以張拉力為變量，運用有限元分析軟件搭建了橋梁模型，并對優化模型進行了可靠性驗證，以期為同類工程進行索力優化提供一定的借鑒與參考。

1 優化模型的建立

1.1 影響矩陣法

1）受調向量。其為結構中控制截面上的k個獨立元素組成的列向量，這些元素接受調整以達到某種期望的狀態，記為

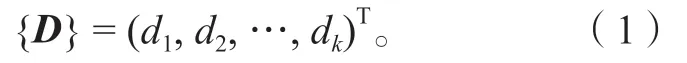
2）調值向量。其由結構中可以進行調整以改變受調向量的n（n＜k）個獨立元素組成的列向量組成，記為

此處施調元素X為吊桿張拉力。

3）影響向量。其為施調向量X中第j個元素發生單位變化時，引起受調向量D的變化向量，記為

4）影響矩陣。n個施調向量分別發生單位變化，將得到的n個影響向量依次排列形成的矩陣即為影響矩陣，記為

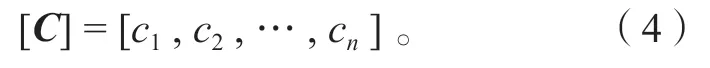
當結構滿足線性疊加原理時，有

1.2 吊桿索力計算

目前針對吊桿內力計算的方法主要有如下兩種：1）剛性支承連續梁法。按照剛性支承連續梁法確定吊桿內力時，以系梁的豎向變形作為控制目標，在保證成橋線型的狀態下對系梁的內力進行優化，其局限之處在于未考慮拱肋的變形情況。2）剛性吊桿法。通過剛性吊桿法計算吊桿的張拉力時，拱肋會在吊桿索力的作用下與吊桿一起產生剛性位移，即吊桿與系梁的連接處將產生豎向撓度，所以這種計算方法也存在一定的局限性。

因剛性支承連續梁法和剛性吊桿法計算吊桿內力均存在一定的局限性，因此，本文擬在趙偉等[10]研究的基礎上，結合影響矩陣法，采用剛性吊桿結合自動調索的綜合分析索力方法，其具體分析過程如圖1所示。

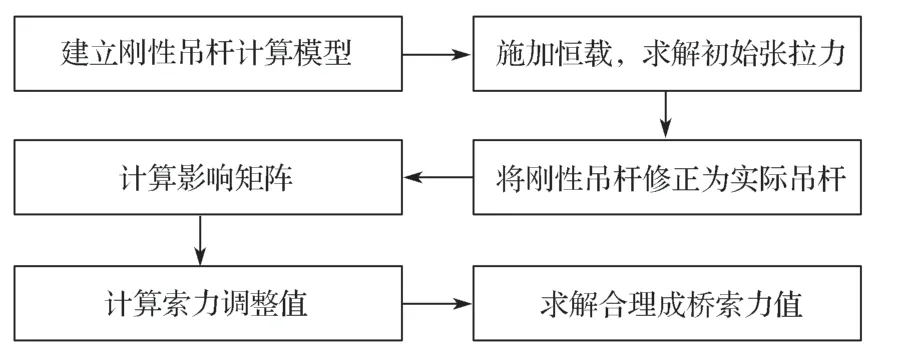
圖1 索力計算流程圖Fig.1 Cable force calculation flow chart

1.3 吊桿索力優化模型

目前，在施工過程中對索力進行調整的方法主要有影響矩陣法[2-3,11-12]和正裝迭代法[13-14]。本文選用影響矩陣法來分析吊桿之間的索力影響關系，吊桿安裝上去時處于無應力狀態，對其施加初次張拉力，然后采取迭代的方式對索力值進行逐步調整，直至其逼近成橋索力設計值。在調整的過程中，最關鍵之處在于假定一個合理的初始張拉力，以使得各吊桿處于受力狀態[15-16]。

在索力為P0的狀態下，對應拱肋的彎矩分布向量為M0，它與期望狀態時的拱肋彎矩分布向量M的差值為

此時若存在一組索力調整量ΔP，滿足：

則索力調整量為

式中：P為優化后的索力；P0為優化前的索力。

對方程（7）進行求解，可以得到施工張拉索力調整值 ΔP。

索力調整之后，將實測索力與設計索力進行比較，若未達到控制范圍內的精度，則在實測索力的基礎上進行迭代計算，直至吊桿索力與設計值間的差值滿足要求。

此外，為使索力受力處于合理狀態，在調整的過程中須滿足以下兩個條件：

1）索力值必須為正，并且不超過其許用應力的40%；

2）相鄰吊桿的索力值差不能過大，要滿足索力的均勻性。

條件1）可表示為

式中：σm為吊桿的應力值；fm為吊桿的設計強度值。

設相鄰的吊桿索力值分別為F1、F2、F3，引入索力不均勻系數[4]：

不均勻索力Zm為

對索力的不均勻性約束可表示為下式：

其中，αm和βm分別為不均勻索力的上限和下限,其具體取值可經過試算得到。

2 工程案例

2.1 工程概況

本工程中，主橋布置為（39.55+168.00+39.55）m 三跨連續梁-系桿拱，全長247.1 m。本橋結構體系為剛性梁、剛性拱。采用雙吊桿結構，全橋共設18 組吊桿，吊桿順橋向間距8 m，橫橋向間距12 m，采用LZM（K）7-73（Ⅰ）型吊桿系統，PES（FD）低應力防腐索體，高強低松弛鍍鋅鋼絲。上、下拱肋計算跨度分別為170.10,165.75 m，設計矢高分別為45,39 m，上、下鋼管拱軸線均采用懸鏈線，系數分別為1.05,1.40。拱肋采用分段吊裝拼接而成，內部填充混凝土。拱腳混凝土分兩次現澆，在現澆第一次混凝土前，應將拱肋鋼管、加勁鋼材等安放到位，拱肋完成后澆筑第二次混凝土。兩榀拱肋之間共設9道橫撐，橫撐均采用空間桁架撐，鋼管內部不填混凝土，其內外表面均需做防腐處理。系梁為單箱三室等高箱梁結構。

2.2 橋梁建模

本研究采用有限元軟件Midas Civil 建立拱橋的有限元模型。模型共計1 248 個單元，單元之間的連接形式分為一般支承和彈性連接兩種，具體的連接方式如表1與圖2所示。

表1 模型中各單元的連接方式Table 1 Connection mode of individual unit in the model

圖2 橋梁模型各單元連接方式示意圖Fig.2 Schematic diagram of the connection mode of individual unit of the bridge model

圖2a 表示箱梁節段與節段之間采用彈性連接的方式進行連接，即建模時對兩節段連接處的節點施加彈性連接；圖2b 表示箱梁與底部的墩臺和支架的一般支承連接方式；圖2c 表示拱圈與拱圈支架的一般支承連接方式。

箱梁底部支架及拱圈支架布置立面圖如圖3所示，為簡化模型，將箱梁底部的支架與拱圈支架簡化為一般支承的連接方式，即對箱梁與底部支架連接處的節點、拱圈與拱圈支架連接處的節點，施加一般支承連接。

圖3 箱梁底部支架及拱圈支架布置立面圖Fig.3 Elevation view of bottom bracket with the arch ring bracket layout of box girder

表2為施工階段的劃分，表3為橋梁模型的材料參數，圖4為橋梁有限元模型示意圖。

表2 施工階段劃分Table 2 Construction phase division

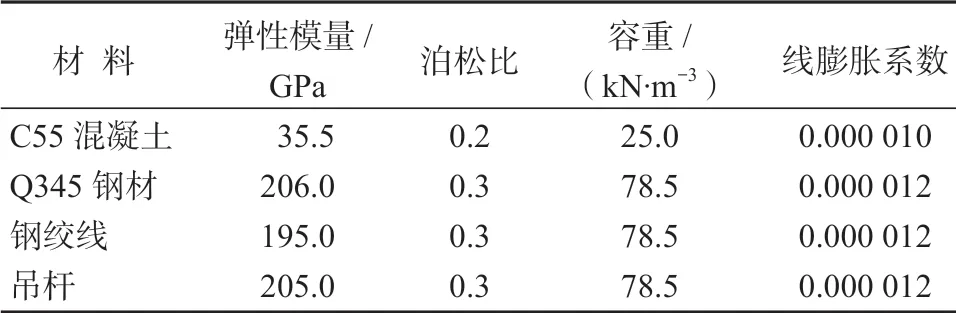
表3 橋梁模型的材料計算參數Table 3 Material calculation parameters of the bridge model

圖4 拱橋有限元模型示意圖Fig.4 Schematic diagram of arch bridge finite element model

模型荷載情況見表4，荷載組合為：

表4 模型荷載參數Table 4 Model load parameters

q恒×1.2+q活×1.4。

橋梁的施工階段共分為8 個階段，首先對系梁進行澆筑，從左至右等分為A1、A2、A3 共3 段進行澆筑；然后，進行拱腳澆筑；其次，進行拱肋的安裝，而拱肋安裝完成后即進行拱肋支架的拆除；接下來進行吊桿張拉；最后，拆除系梁底部的貝雷梁。

2.3 優化結果

本橋為對稱結構，因此只需要取半幅進行研究。首先，基于1.2 節的方法，采用剛性吊桿法計算出吊桿索力值。將吊桿橫截面積增大100 倍，同時將其質量減小為原來的1/100，近似為剛性結構，計算得到的吊桿索力值如表5所示。

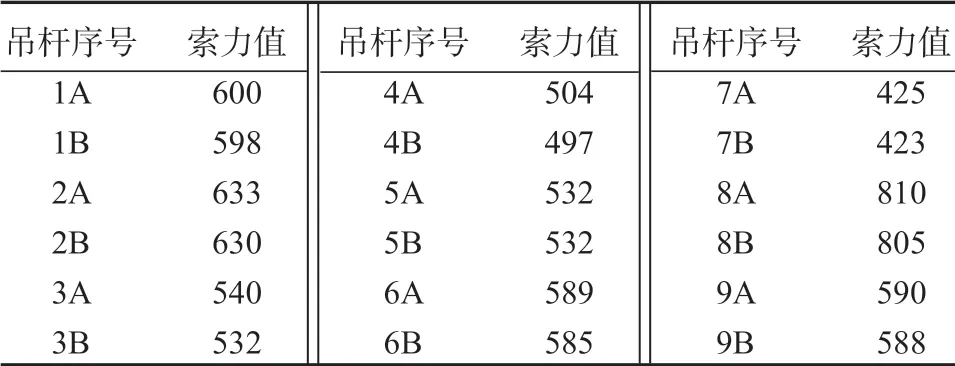
表5 剛性吊桿法計算得到的索力值Table 5 Cable force values by rigid suspender method kN

將表5中的索力值代入有限元模型，可得到成橋狀態下的吊桿索力計算值P1，將其與設計索力值P0進行比較，可得到索力調整值：

然后由式（7）來計算施工張拉調整值。將調整后的索力值代入有限元模型，即可得到調整后的成橋索力計算值，如表6所示。

表6 第一次優化后的成橋索力值Table 6 Cable force values of the bridge after the first optimization

從表6中可以發現，成橋索力計算值和設計值差別最大處為5A 和5B，差值率分別為11.2%,10.5%。在實測索力的基礎上，進行迭代計算，得到第二次優化的吊桿施工張拉力，如表7所示。

表7 第二次優化后的成橋索力值Table 7 Cable force values of the bridge after the second optimization

圖5所示為優化后計算索力與設計索力的差值率。由圖可知，經過兩次優化后，成橋索力與設計索力的差值率控制在±3%的范圍內，滿足施工控制要求。

圖5 剛性結構吊桿的計算索力與設計索力差值率Fig.5 Difference between the calculated cable force and the design cable force of the rigid structure suspender

本研究同時采用王新征等[14]基于正裝迭代法及最小二乘法原理所建立的索力優化模型，對本項目進行索力優化，所得計算索力與設計索力的差值率結果如圖6所示。由圖6可以發現：在第一次索力優化過程中，造成的最大誤差率為13%；在第二次優化過程中，造成的最大誤差率為8%，而本文所建立的索力優化模型，經過兩次優化后，能將誤差率控制在±3%的范圍之內。

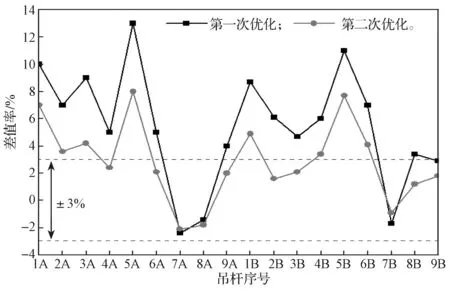
圖6 文獻[14]中優化模型的計算索力與設計索力差值率Fig.6 Difference between the calculated cable force and the design cable force of the optimized model in literature [14]

通過有限元模型，可得成橋狀態下拱橋各部位的變形情況。圖7～9 分別為系梁、上拱肋和下拱肋不同位置處的設計撓度值與優化后撓度值變化曲線。

由圖7～9不難發現，經過兩次優化后，進行張拉的系梁撓度與設計的系梁撓度大致相同，兩者差別最大的地方發生在距系梁中心的水平距離48 m 處，差值為6.04%。此外，優化前后上下兩榀拱肋的豎向撓度也基本一致，兩者差別最大的地方分別發生在距拱肋中心的水平距離48 m 處和52 m 處，差值分別為6.57%,4.80%。

圖7 系梁恒載撓度曲線Fig.7 Tie beam dead load deflection curves

圖8 上拱肋恒載撓度曲線Fig.8 Dead load deflection curves of the upper arch rib

圖9 下拱肋恒載撓度曲線Fig.9 Dead load deflection curves of the lower arch rib

3 結論

本文結合東海特大橋系桿拱連續梁，在影響矩陣法的基礎上，以優化吊桿張拉次數為目標，建立了吊桿的索力優化模型，同時運用Midas Civil 建立拱橋的有限元模型，對索力優化模型的可靠性進行了驗證，研究結果表明：

1）經過兩次對施工張拉索力進行調整后，吊桿的成橋索力值與設計索力值的差值控制在±3%的范圍之內，滿足施工控制要求；

2）成功地將吊桿張拉次數縮減為兩次，大大縮短了工期；

3）優化后上下拱圈及系梁的變形量與設計撓度基本相同，差別最大的為6.57%。

此外，本模型在構建的過程中沒有將拱肋的軸力納入約束條件，在接下來的研究中，可以考慮將其作為約束條件，對張拉模型進行完善。