基于轉動慣量辨識與擾動補償的永磁同步電機滑模控制

李江坪，王 兵，顏偉平，郭皓源，李 羅

（1.湖南工業大學 電氣與信息工程學院，湖南 株洲 412007；2.湖南工業大學 電傳動控制與智能裝備湖南省重點實驗室，湖南 株洲 412007）

1 研究背景

在工程應用中，電機的運行容易受到多方面干擾的影響，例如電機的內部參數攝動和負載轉矩波動都有可能影響電機的正常運行，其中轉動慣量也會隨著負載的變化而發生改變，而負載擾動就是調速系統最大的干擾，也是影響最大的一個因素。對于抗負載擾動要求比較高的系統而言，控制系統的抗負載擾動性能和控制精度的要求就顯得尤為重要[1]。

當采用PI 調節器對永磁同步電機（permanent magnet synchronous motor，PMSM）進行控制時，控制器的調節算法相對較為簡單，在一定范圍內可以滿足系統控制要求，但是對于一些高精度、高性能的場合，傳統的PI 調節器可能因存在著一些缺陷而達不到理想的控制效果[2]。采用滑模變結構控制（sliding mode control，SMC），可以減小系統參數攝動和外界擾動對系統整體性能的影響，具有很強的魯棒性，可以彌補PI 調節器存在的部分不足之處，但是它有一個缺點，就是存在著固有的抖振現象，當狀態軌跡到達滑模面后，并不是沿著滑模面平穩地向著平衡點滑動，而是在滑模面兩側來回穿插，從而使系統產生了難以消除的抖振現象。在滑模控制方面，很多專家和學者都在不斷地進行改進研究，希望能盡可能地抑制滑模的抖振現象，達到提高其控制性能的效果[3]。如文獻[4]采用等價輸入干擾估計算法，對干擾起估計和抑制作用，并且引入了電流前饋，以減小電流脈動，對系統的響應速度和抗擾性能有很大的優化效果，但是沒有考慮因負載改變引起的轉動慣量發生變化，因而會對控制系統觀測值產生影響。文獻[5-6]為了解決負載轉動慣量在辨識過程中出現的精度不夠等問題，設計了一種通過抑制內干擾力矩控制策略的干擾觀測器，從而使電機的轉速更加穩定，輸出力矩響應也更為快速。文獻[7]提出了一種模型參考自適應（model reference adaptation system，MRAS）控制方法和滑模變結構理論相結合的負載觀測器，仿真實驗結果表明該觀測器能實時跟蹤且準確地檢測出負載轉矩的變化情況，從而提高了調速系統的整體性能，但是調節時間較長，不適用于快速調節的控制系統研究。文獻[8]提出了一種將電機轉速和負載轉矩同時作為觀測對象的滑模觀測器，并將觀測的負載轉矩進行前饋補償的方法，實驗結果表明該方法對系統抖振現象和抗擾性能都有較好的改善效果。文獻[9]設計了一種改進滑模觀測器的PMSM矢量控制方法，用于解決傳統滑模觀測器在PMSM 轉子位置和轉速觀測時存在的抖振問題，但是在轉速環的設計中，滑模參數的選取較為困難，不易調節。文獻[10-11]將大多數學者默認為固定不變的電機整體轉動慣量進行快速、準確地在線跟蹤辨識，對控制算法中的轉動慣量實時更新，可以有效地提高系統的抗干擾性能，但只是針對于突擊負載的分析，對于大慣性負載來說，電機運行是一個連續變化的量，對電機的影響需要進行更深入地研究。

基于上述分析，本文提出一種輸入干擾補償的方法來對電機的內部參數攝動和外部負載干擾進行擾動抑制的控制策略，并結合MRAS 控制方法，設計了一種轉動慣量在線辨識擾動補償觀測器，實時將辨識出的轉動慣量反饋至觀測器中，即將轉矩辨識的結果轉換為觀測電流，與給定轉速經滑模控制輸出電流做差后，輸入控制端，對控制系統進行輸入干擾補償的方式，以減小電流脈動，使電機達到穩定運行的效果。在環實物仿真平臺驗證結果表明，本研究所提出的控制策略對系統抗擾性能和響應速度都取得了很好的改善效果。

2 PMSM 的數學模型

為了方便研究設計，采用id=0 的控制方法作為轉子磁場定向控制，則PMSM 在旋轉坐標系下的電壓方程如下：

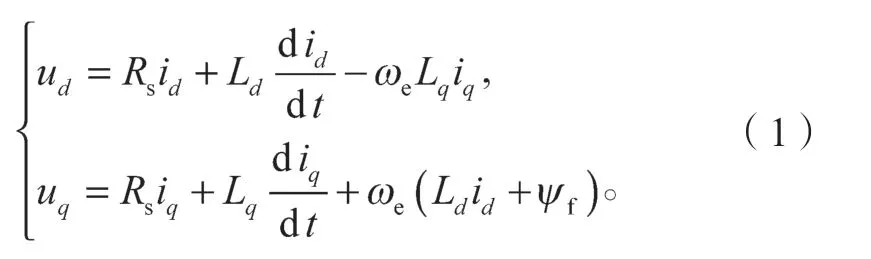
式中：ud、uq、id、iq、Ld、Lq分別為電機在直軸和交軸的電壓分量、電流分量以及電感；

Rs為定子電阻；

ωe為電角速度；

ψf為永磁體磁鏈。

對于采用id=0 控制的永磁同步電機控制系統，若Ld=Lq，則不存在磁阻轉矩，此時，轉矩方程為

電機的運動方程為

式（2）（3）中：Te為電磁轉矩；

p為極對數；

TL為負載轉矩；

J為轉動慣量；

Br為電機的黏滯摩擦系數；

ωm為機械角速度。

3 滑模速度控制器

在滑模變結構控制系統中，滑模控制的設計主要包含了3 個要素，分別是切換函數s、趨近律和控制率i*q[12]。

3.1 滑模控制器設計

定義PMSM 系統的狀態變量如下：

式中：ω*為給定轉速值；

ω為實際轉速值。

為使系統更快達到穩態，定義切換函數為

式中c為滑模面參數，滿足李普希茲條件，且c＞0。

為提高滑模趨近運動中的動態性能，消除滑模控制系統的抖振現象，引用了高為炳院士提出的指數趨近律概念設計控制器[13]，其表達式為

式中：k1、k2均為調節參數；

-k1sgn(s)為等速趨近項；

-k2s為指數趨近項。

由式（8）可知，通過調節參數k1和k2，不僅可以解決滑模運動趨近過程的運動性能，還可以有效地削弱系統抖振現象。

為加快控制系統的調節時間，使系統在受到干擾的情況下能快速恢復到穩定狀態，引用文獻[14]中的指數趨近律方法，并改進為

在指數趨近律的指數項中，加入了轉速誤差平方x12，使參數k2與系統狀態變量相結合，形成變指數趨近律。當系統狀態變量的運動軌跡遠離滑模面時，此時指數項中x12的值逐漸增大，狀態變量將以等速-k1sgn(s)和變指數-k2x12s兩種速度趨近滑模面；當系統狀態變量運動軌跡靠近滑模面時，指數項中x12的值近似為0，指數項的值也趨近為0。通過這種方式趨近時，等速項參數應盡可能地取小，這樣可以減小因趨近滑模面的速度過大而引起系統抖振的現象，使控制器的調節更加穩定。

聯立式（7）和式（9），可得：

由式（10）可得，基于改進指數趨近律的滑模轉速控制器的設計，定子電流分量iq的給定值為

3.2 穩定性分析

為了證明系統可以由任意初始狀態下在有限時間內收斂，即能保證運動軌跡可以到達滑模面，選取李雅普諾夫函數為

由式（9）和式（12）可以得到

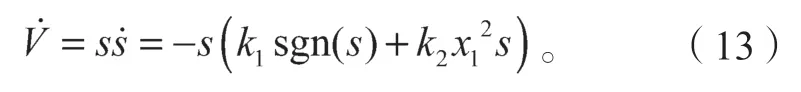
而k1＞0、k2＞0、s·sgn(s)≥0、x21≥0，因此可以得到，即設計的控制系統可以達到穩定。

4 負載擾動補償觀測器

為了提高系統的抗負載性能和增強系統的穩定性，本研究采用一種擾動補償觀測器，對負載轉矩進行同步估算，然后通過前饋補償的方式，對系統進行擾動補償，以減小控制電流的脈動，從而實現對系統穩定性能的提升和對系統動態性能的改善。設系統的狀態方程如下：

式中：x為系統狀態變量；

u為輸入控制量；

f為負載擾動量；

A、B、D均為常系數矩陣。

則負載擾動誤差可表示為

e為擾動量的觀測誤差。

若在一個采樣周期內，不考慮負載擾動量f的變化，即，通過擾動補償觀測器進行推算，構建如下觀測器表達式：

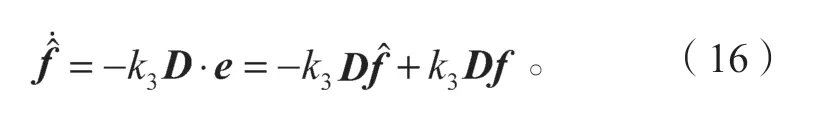
式中：k3為擾動補償觀測器的增益系數。

將式（16）代入式（14），可得：

在控制系統中，由于系統的采樣周期速率很快，對于負載而言，在一個采樣周期內，負載轉矩的變化是可忽略不計的，因此一個變化周期的負載轉矩可作為恒定值來進行分析，即，將電機機械轉速和負載轉矩作為狀態變量，則式（3）可改寫成如下形式：

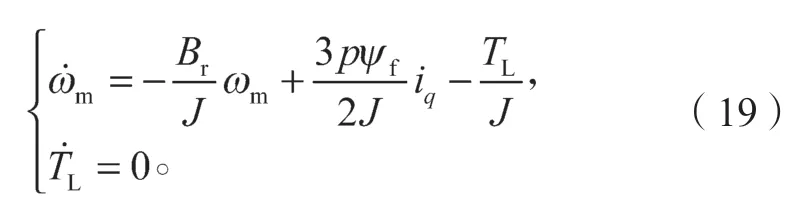
擾動補償轉矩觀測器的結構如圖1所示。

圖1 擾動補償轉矩觀測器結構圖Fig.1 Structure diagram of disturbance compensation torque observer

由于負載轉矩估算結果不能直接與轉速形成閉環反饋，故將觀測的負載轉矩轉換為補償電流作為負載擾動補償輸入控制調節器中。設補償電流為，結合式（11），可得到控制端給定電流為

式中，kt為轉矩觀測補償系數，且kt＞0。

由式（2）中電磁轉矩與電流之間的關系，可得出kt應取2/(3pψf)。

5 轉動慣量辨識

因系統轉動慣量會隨著負載的擾動變化而發生相應改變，可見，轉動慣量對系統的控制具有很大的影響，要使得系統的抗干擾性能提高、魯棒性加強，就不能忽略負載對系統轉動慣量的影響。本文采用MRAS 的辨識方法在線辨識系統轉動慣量，MRAS結構圖見圖2。

圖2 MRAS 結構圖Fig.2 MRAS structure diagram

如圖2所示，MRAS 由3 部分組成，包括可調模型、參考模型和辨識算法。將含轉速的模型視作可調模型，用ωg表示，它表示實際的物理系統；將不含轉速的模型視作參考模型，用ωm表示，它表示理論的數學模型系統。將可調模型和參考模型做差，得到速度觀測誤差值ε，ε作為辨識算法的輸入參數，形成一個自適應算法實時調節，實現對系統整體J的實時跟蹤辨識。

設Ts為系統采樣周期，將PMSM 運動方程進行離散化處理，黏滯摩擦轉矩此時忽略不計，則t-1 時刻的離散化方程為

同理，t-2 時刻的離散化方程為

系統的采樣頻率遠大于負載的變化速率，在一個采樣周期內，負載轉矩TL的變化可以忽略不計，默認為保持不變，即TL(t-1)=TL(t-2)，聯立式（22）和（23），可得出MRAS 的參考模型為

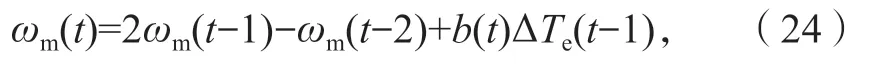
式中：b(t)=Ts/J；

ΔTe(t-1)=Te(t-1)-Te(t-2)。

同理，MRAS 的可調模型表達式為

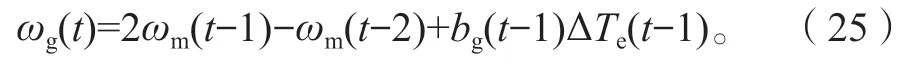
式中：ωg(t)為t時刻實際電機轉速的觀測值；

ωm(t)為t時刻實際電機轉速的實際值；

bg(t-1)為辨識算法的輸出量。

引用Popov 超穩定理論設計辨識算法，推導出轉動慣量的自適應辨識算法表達式，為

式中：ε(t)為速度觀測誤差，且ε(t)=ωm(t)-ωg(t)；

β為自適應的增益參數。

在得到bg(t)后，可通過J*=Ts/bg(t)計算得出轉動慣量觀測值J*。

6 在環實物仿真平臺驗證

為了驗證上述方法的可行性，通過Matlab 搭建仿真模型，并借助MS320F28335 型DSP 為核心的模型在環實物驗證平臺進行驗證。

在環實物仿真平臺所選用的PMSM 的具體參數如表1所示。

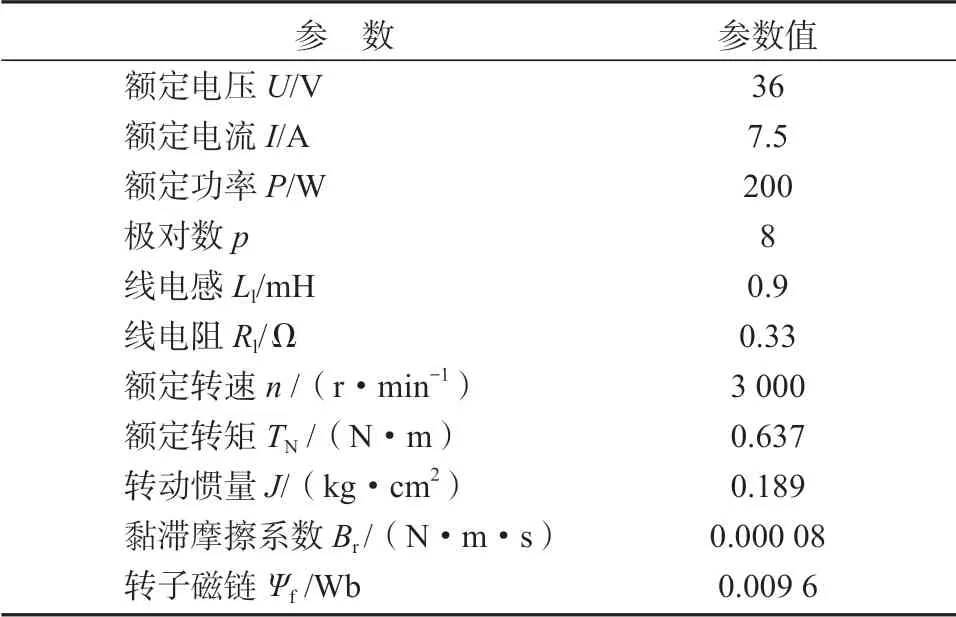
表1 選用PMSM 的參數及取值Table 1 PMSM parameters with their values

在環實物仿真平臺中，實物電機帶的編碼器為增量式編碼器ABZ+uvw，2 500 PPR，每次上電時無法知道自己的絕對位置，采用在程序前2 s，先給定3π/2 的電角度，以消除初始電角度偏差。在環實物仿真平臺以及仿真模型分別如圖3和圖4所示，控制系統原理框圖如圖5所示。

圖3 在環實物仿真實驗平臺Fig.3 In-the-loop physical simulation experiment platform

圖4 在環實物仿真模型Fig.4 In-the-loop physical simulation model

圖5 控制系統原理框圖Fig.5 Block diagram of the control system

6.1 轉動慣量辨識驗證

通過仿真驗證可以得知，辨識算法能很好地辨識出系統整體的轉動慣量值，負載的擾動也會引起轉動慣量發生改變。同時，當取不同的自適應增益系數時，轉動慣量辨識的調節過程也會有不同的變化。即在給定轉速為1 200 r/min 的情況下，空載啟動，分別取不同的β值，即β=0.1,0.5,1.0,2.0，對電機進行轉動慣量辨識，觀察在受到干擾的情況下對轉動慣量辨識的影響，所得結果如圖6所示。

圖6 不同增益系數時轉動慣量辨識波形Fig.6 Moment of inertia identification waveform under different gain coefficients

分析圖6所示不同增益系數時轉動慣量的波形變化情況可以得出：隨著自適應增益系數取值的增大，轉動慣量辨識響應速度加快，不過與此同時辨識出的結果會有較大的波動。

6.2 負載轉矩測量值與觀測值對比分析

圖7所示為仿真所得扭矩傳感器的轉矩檢測值變化曲線，圖8所示為仿真所得擾動補償觀測器的觀測值變化曲線。

圖7 扭矩傳感器的轉矩檢測值變化曲線Fig.7 The curve of torque detection value of the torque sensor

圖8 擾動補償觀測器的觀測值變化曲線Fig.8 Curves of observed values of the disturbance compensation observer

電機上電穩定后，空載啟動，從扭矩傳感器的轉矩檢測值變化曲線中（見圖7）可以看出，當電機空載運行時，扭矩傳感器測量出的轉矩為0.11 N·m；當給定的負載轉矩為0.22 N·m，扭矩傳感器在10 s 時測量所得的轉矩為0.33 N·m。

由圖8可以得知，觀測器觀測到的轉矩值也為0.33 N·m，說明擾動補償觀測器對負載轉矩的變化具有實時的跟蹤補償能力。

在實驗過程中，將觀測器的觀測值與實際的扭矩傳感器測量值經過多次試驗對比與分析發現，在轉速恒定的情況下，擾動觀測器的增益系數k3對觀測效果有很大的影響。增益系數k3值越小，系統響應速度越快，觀測值的跳動幅度越大；而k3值越大，系統響應速度越慢，觀測值的跳動幅度越小。因此，k3應折中選取一個相對合適的值。

6.3 負載力矩突變分析

電機采用空載啟動，在轉速恒定的情況下，連續改變電機的負載力矩。即電機上電穩定后，給電機設定1 200 r/min 的恒定轉速；運行至10 s 時，突加大小為0.22 N·m 的負載力矩；運行至14 s 時，突加大小為-0.22 N·m 的反向負載力矩。圖9所示為力矩突變情況下，加負載擾動補償后與未加負載擾動補償時的電機轉速對比仿真結果。

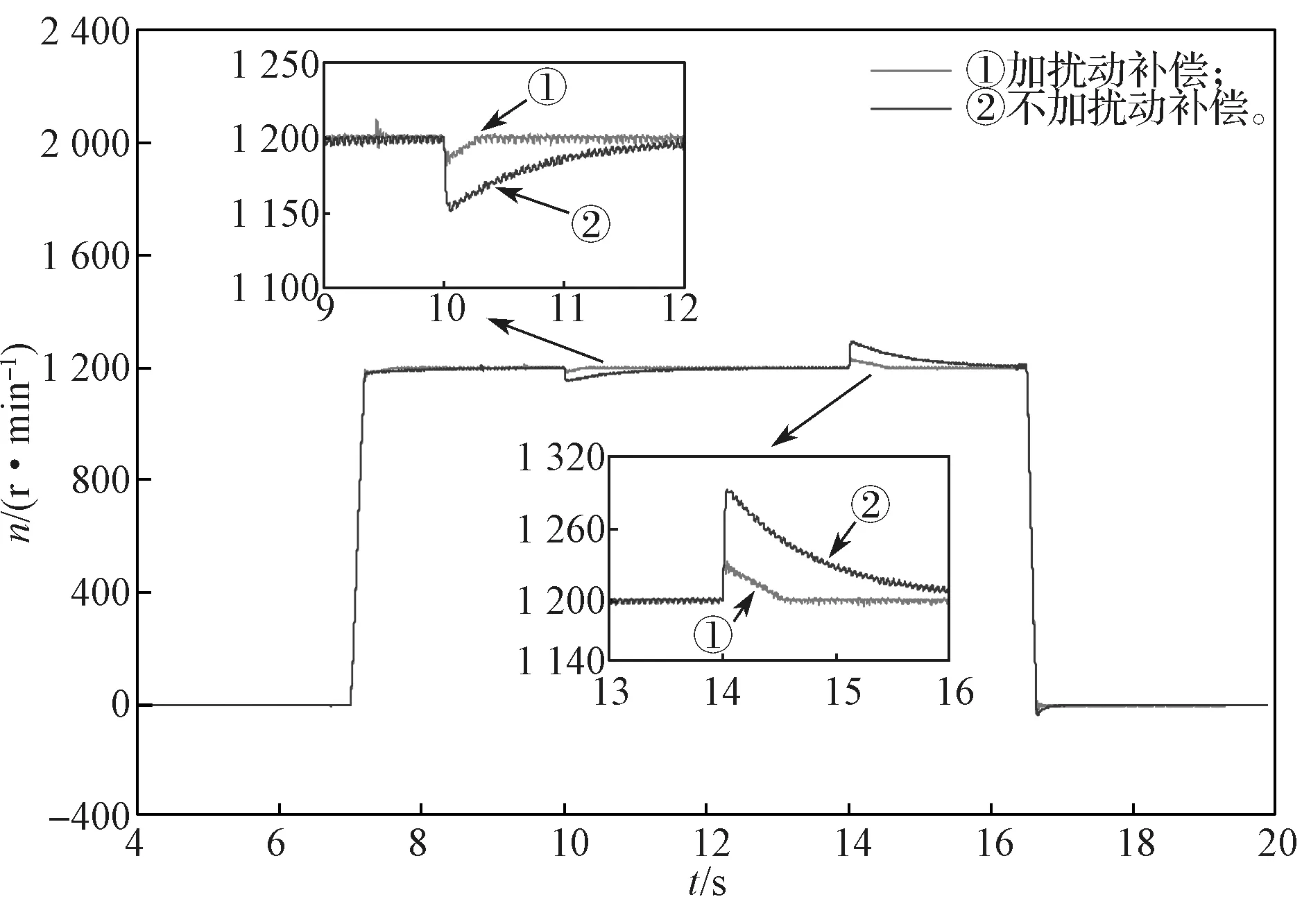
圖9 兩種控制策略下力矩突變時的轉速對比曲線Fig.9 Comparison of torque mutation speed under two control strategies

從圖9中可以看出，在不加擾動補償的控制系統中，當負載發生突變時，電機轉速有50～90 r/min 的跌落和上升現象，需要2 s 左右即恢復到給定的轉速；在加擾動補償的控制系統中，當電機轉速跌落和上升減小到20～30 r/min 時，僅需要0.5 s 左右便可恢復到給定轉速。由此可見，經過負載擾動補償后的調節時間明顯縮短，并且能快速恢復到給定轉速，比未加擾動補償的控制響應更快，具有較好的抗干擾能力和響應速度。

6.4 電機轉速突變分析

在沒有外界干擾的情況下，給電機加載恒定的負載力矩，但連續改變電機的轉速。即當電機上電穩定后，將電機轉速設定為1 200 r/min，在10 s 時，轉速從1 200 r/min 升到1 500 r/min，運行至14 s 時，再將轉速從1 500 r/min 突降至1 300 r/min，所得的實物對比仿真結果如圖10 所示。

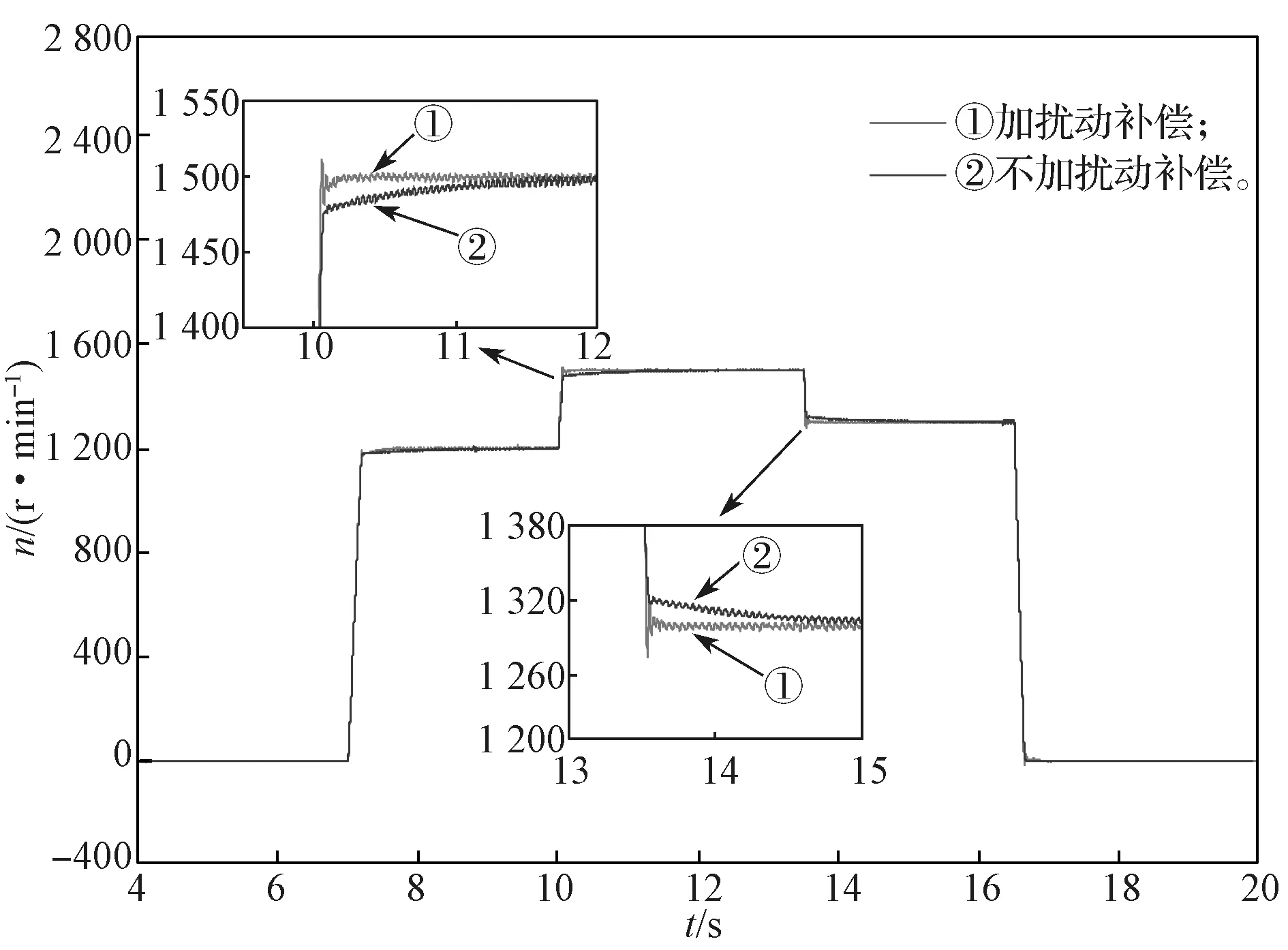
圖10 兩種控制策略下轉速突變響應的實物對比仿真結果Fig.10 Comparison of actual speed change response under two control strategies

從圖10 所示仿真實驗結果圖中可以看出，未加擾動補償時，系統的響應速度較慢，大概需要1.5 s才能穩定到給定的轉速；而當加入擾動補償后，系統的響應速度明顯加快，調節時間縮短，但是會有較小的超調量。

7 結語

本研究設計了一種轉動慣量在線辨識擾動補償觀測器，將辨識出的轉動慣量實時反饋至觀測器中，采用一種輸入干擾補償的方法，將觀測的負載轉矩變化值轉換為轉矩電流，補償至控制系統中，以減小轉矩電流脈動，提高系統的穩定性能。在環實物驗證仿真結果表明，所設計的轉動慣量在線辨識擾動補償觀測器能很好地對負載轉矩進行觀測，引入輸入干擾補償后的系統響應速度更快，抗干擾性能更強，具有較好的魯棒性。