基于擴展克雷洛夫角的全姿態導航解算方法

魏宗康，高榮榮

（北京航天控制儀器研究所，北京 100854）

捷聯式慣性系統與載體直接固連，通過陀螺儀測量角速度并經數學解算后給出三個姿態角的值。一般情況下，確定姿態信息的方法有方向余弦運動法、歐拉-克雷洛夫角法和四元數法等。方向余弦法的優點是直接可求得動系和定系之間的坐標變換矩陣，但缺點是計算量較大，因此，該方法并沒有應用于工程中。目前，應用最多的是四元數法[1-3]，其思路是先根據4個元素求解動系相對定系的坐標變換矩陣，然后再依據該坐標變換矩陣求解三個姿態角，但缺點是在求解姿態角過程中存在多值問題和奇異值問題。歐拉-克雷洛夫角法雖可直接通過3個角速度微分方程解算出姿態角，但缺點是解算值的大小與不同的3次轉動順序相關，且中間旋轉角度接近90 °時方程會出現退化現象，導致精度下降，因此，歐拉-克雷洛夫角法不適用于運載體全姿態運動時的姿態解算[4,5]。

工程中為了回避姿態角解算過程中的多值問題，通過限定載體的角運動范圍以確保解算的姿態角與真實值一致[6,7]。比如，對于航天器等非大機動飛行場合，通過限定姿態角范圍既回避了多值問題，又規避了奇異值問題，將俯仰角或航向角限定在（-90 °, +90 °）范圍內[8]。

但對于取消滾動控制的大機動全姿態飛行場合，很顯然繼續采用限定姿態角范圍將不滿足使用要求。目前，解決多值問題和奇異值問題的主要措施是雙歐拉角法，其主要思想都是通過改變不同歐拉角組合、相互切換的方法克服奇異值問題。例如，在文獻[9]中，為了解決魚雷俯仰角為90 °時正確的偏航角和橫滾角的解算問題，將雙歐拉法引入到空投魚雷的六自由度方程中，通過交替使用雙歐拉方程正確反映了空投魚雷的運動規律，為魚雷大幅度全姿態運動的空投彈道研究提供了有意義的理論參考。在文獻[10]中，針對垂直發射的地空導彈在大機動飛行時姿態解算出現的奇異值問題，將正、反歐拉角微分方程切換的雙歐拉全姿態解算方法應用到姿態解算過程中，并通過半物理試驗驗證了該方法在工程上的有效性。在文獻[11]中，同樣利用正、反歐拉方程在傘、彈系統中克服了歐拉方程的奇異性，并通過與四元數法的姿態解算精度進行對比，認為雙歐拉法在空間飛行時間較長的傘-彈系統來說，雙歐拉法更具優勢。

上述雙歐拉全姿態方法雖然解決了俯仰角在±90 °時的奇異值問題，但是此方法的第一個缺點是需要根據俯仰角范圍選定正或反歐拉微分方程，因此，在計算方面，運用到6個歐拉角和2套歐拉微分方程，且需要實時判定俯仰角的范圍，一方面增加了較大計算量、存儲量和切換流程，另一方面對系統的解算和控制周期有嚴格的要求[12]。第二個缺點是單個歐拉方程無論怎樣順序變換，一個歐拉方程都必然會出現一個姿態角在± 90 °時處于奇異值狀態，因此，正歐拉方程中俯仰角在± 90 °時奇異，那么反歐拉方程解決了俯仰角為± 90 °時的奇異問題，但是出現了偏航角或者滾轉角不能工作在± 90 °時的問題。以上兩個缺點說明雙歐拉角并不能實現真正意義上的全姿態。

針對四元數法、克雷洛夫角法以及雙歐拉角法存在的不足之處，本文提出了基于擴展克雷洛夫角的全姿態導航解算方法，該導航解算的姿態矩陣由四個旋轉角度依次旋轉得到。針對該姿態矩陣的冗余性，采用因果控制策略以實現唯一的結果響應。在整個解算過程中，不會發生某一旋轉角度在90 °時引起奇異值的現象，實現了全姿態高精度導航解算。

1 基于四元數法求解姿態角時存在的不足之處

采用四元數求解的坐標變換矩陣是唯一的，但是，變換矩陣中的四個元素只是中間變量，在通過坐標變換矩陣解算出姿態角的過程中存在以下兩個不足之處。

1.1 多值問題

導航坐標系相對本體坐標系按照相同的旋轉順序時，姿態角也不唯一，即一個坐標變換矩陣可以用兩組不同的姿態角表述。比如，除一組姿態角φ、ψ、γ外，還可用另一組姿態角φ-π、π-ψ、γ-π表述，即：

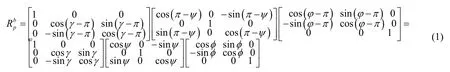
1.2 奇異值問題

在式(1)中，當ψ=90 °時，坐標變換矩陣為：

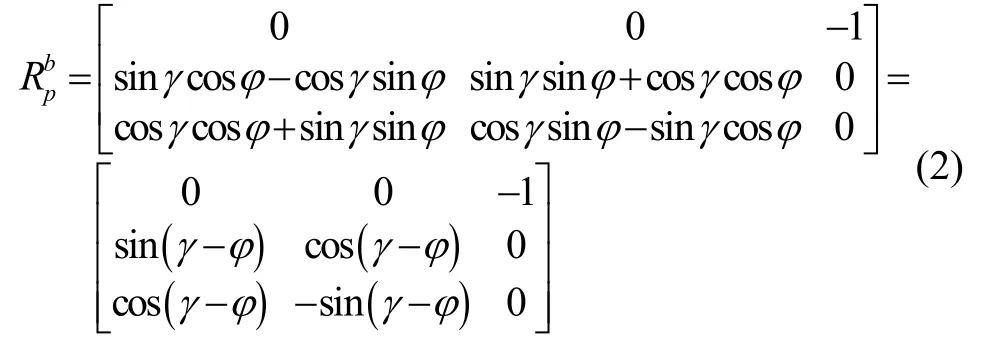
從式(2)可以看出，不能求出姿態角φ、γ獨立的值，而只能求出二者之差γ-φ。滿足該差值的φ和γ有無窮多個，因此，在工程實際中可把其中一個姿態角設置為零，比如φ= 0 °，而另外一個姿態角取為γ=γ-φ。但這種方法的缺點是φ的真值如果不為零時，則兩個角度的值都與真值不相符。

2 基于克雷洛夫角求解姿態角時存在的不足之處

采用克雷洛夫角可描述導航坐標系經過三次轉動后到達本體坐標系的過程，坐標變換矩陣也是唯一的，但受限于轉動順序，導致具體轉動過程中角度值不同。

2.1 以z→y→x順序轉動的克雷洛夫角法

以z→y→x順序轉動的具體過程為：導航坐標系Oxyz繞Oz軸轉動φ1角，到達OLNz；OLNz再繞ON軸轉動ψ1角，到達Ox′NM；最后，Ox′NM繞Ox′軸轉動γ1角，到達Ox′y′z′。列寫出用姿態角φ1、ψ1、γ1描述的坐標變換矩陣為：

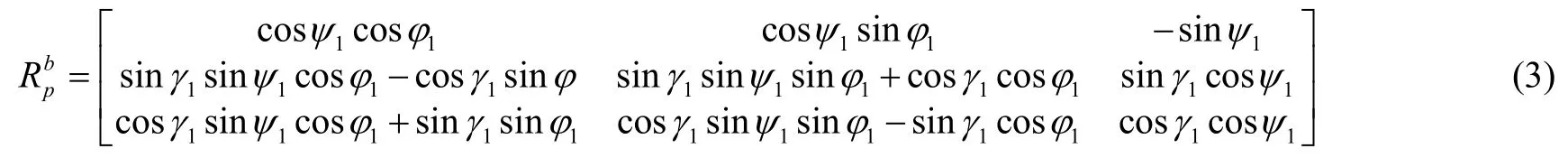
則三個克雷洛夫角對應的角速度方程為：

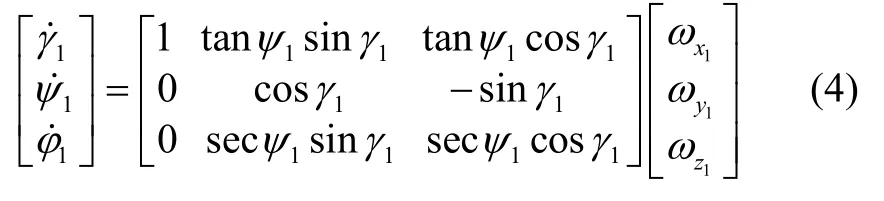
其中，ωx1、ωy1、ωz1分別為捷聯式慣性系統的本體沿X、Y、Z三個方向相對導航坐標系的角速度。

由式(4)可知，偏航角ψ1在± 90 °時奇異，無法滿足此導航模式下的高精度解算需求。

2.2 以z→x→y順序轉動的克雷洛夫角法

以z→x→y順序轉動的具體過程為：導航坐標系Oxyz繞Oz軸轉動φ2角，到達OLNz；OLNz再繞OL軸轉動γ2角，到達OLy′M；最后，OLy′M繞Oy′軸轉動ψ2角，到達Ox′y′z′。列寫出用姿態角φ2、ψ2、γ2描述的坐標變換矩陣為：

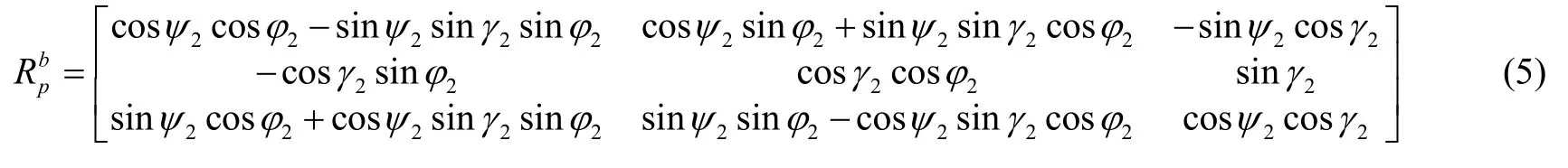
三個克雷洛夫角γ2、ψ2、φ2對應的角速度方程為

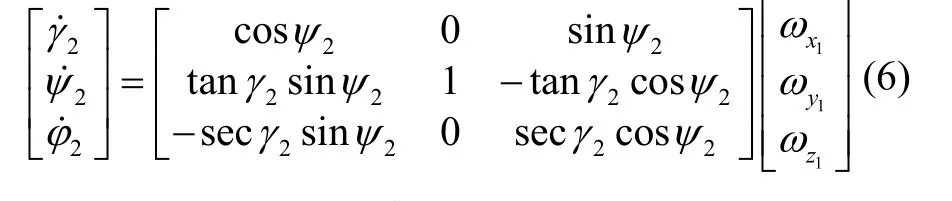
由式(6)可知，橫滾角γ2在± 90 °時奇異，無法滿足此導航模式下的高精度解算需求。

3 基于雙歐拉法求解姿態角時存在的不足之處

為避免采用式(4)或式(6)的微分方程進行導航解算時克雷洛夫角的奇異值，提出了一種基于雙歐拉法的姿態解算方法[7-9]，主要思路為：

(a)當ψ1∈[-45 °, +45 °]或ψ1∈[135 °, 225 °]時，式(4)不存在奇異值，則可直接采用該式計算得到γ1、ψ1、φ1，以及坐標變換矩陣如式(3)。

由于式(3)表示的坐標變換矩陣也可表示為式(5)，因此，可解算出：

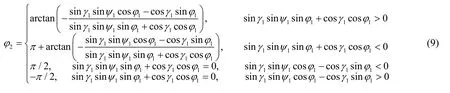
(b)當區間ψ1∈[-135 °, -45 °]或ψ1∈[45 °, 135 °]時，式(4)可能存在奇異值，為此，可采用式(6)得到γ2、ψ2、φ2以及坐標變換矩陣如式(5)。由于式(5)表示的坐標變換矩陣也可表示為式(3)，因此，在限定|ψ1|＜90 °的前提下，可求得：

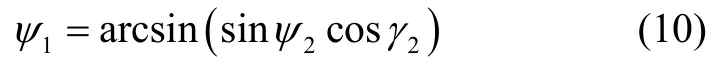
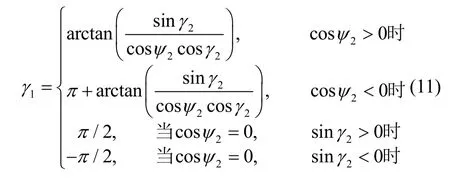
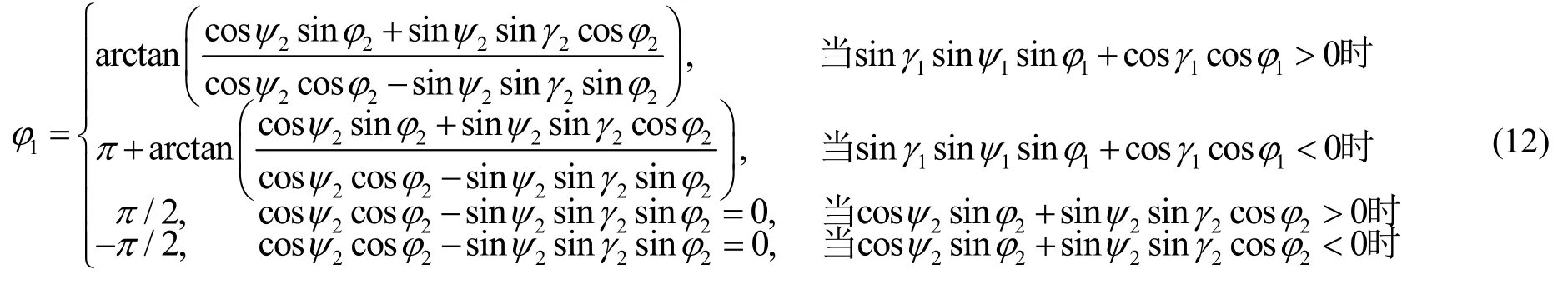
上述基于雙歐拉法的姿態解算方法主要是避免了ψ1→90 °的情況，但不能保證γ2不會趨于90 °。換句話說，如果以γ2作為區間切換基準角度，當γ2∈[-45 °, +45 °]或γ2∈[135 °, 225 °]時，可直接采用式(6)得 到γ2、ψ2、φ2；而 當γ2∈[-135 °, -45 °]或γ2∈[45 °, 135 °]時，采用式(4)解算γ1、ψ1、φ1，此時的量化誤差又很大。因此，需要事先已知哪種轉動順序不會出現奇異值。既然如此，只需采用不會出現奇異值的轉動順序的克雷洛夫角進行姿態解算即可，而不需要所謂的“雙歐拉法”。另外，采用雙歐拉法需要兩組克雷洛夫角、共6個參數，計算量增大。

4 基于四次旋轉的擴展克雷洛夫角全姿態解算

基于三次轉動的克雷洛夫角姿態解算方法在中間角度接近90 °時會引起動態誤差，且通過雙歐拉角法仍無法完全實現全部三個姿態角的全姿態導航解算。本節提出一種基于四個旋轉角度的擴展克雷洛夫角全姿態解算方法，可有效避免該現象的發生。

4.1 擴展克雷洛夫角的冗余性

擴展克雷洛夫角是在原三次轉動定義的克雷洛夫角基礎上再增加一次轉動后形成的四個轉動角度。如圖1描述的具體轉動過程為：導航坐標系Oxyz繞Oz軸轉動φ角，到達OLNz；OLNz再繞ON軸轉動ψ角，到達OQNM；OQNM繞OQ軸轉動γ角，到達OQy′P；最后，OQy′P繞Oy′轉動ξ角，到達Ox′y′z′。

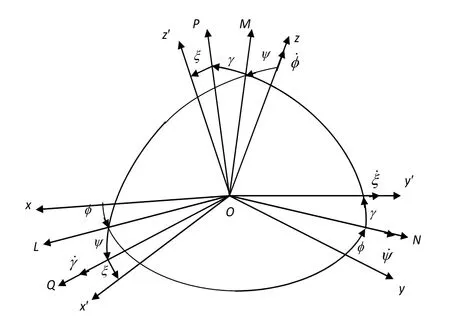
圖1 基于擴展克雷洛夫角的載體系相對導航系的轉動Fig.1 rotation of the body system relative to navigation system based on extended Krylov angle

列寫出用姿態角φ、ψ、γ、ξ描述的坐標變換矩陣為：

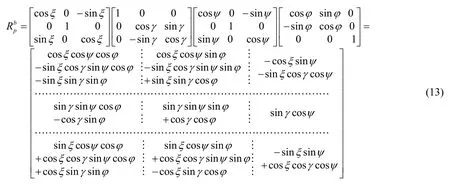
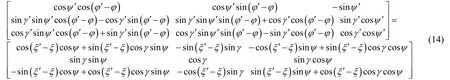
根據式(14)可解出兩組框架角的制約關系為：

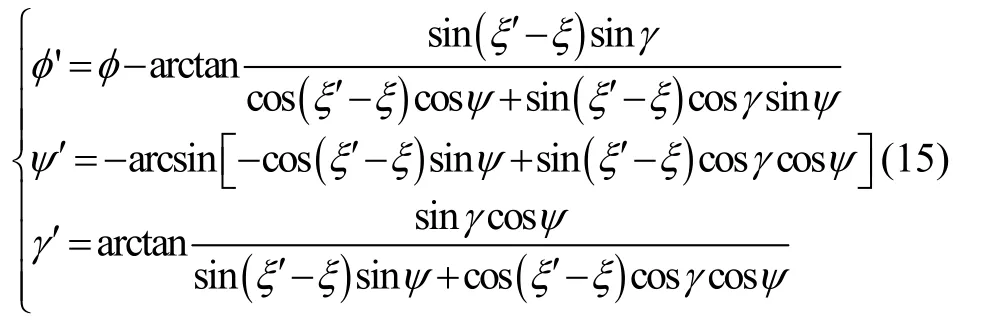
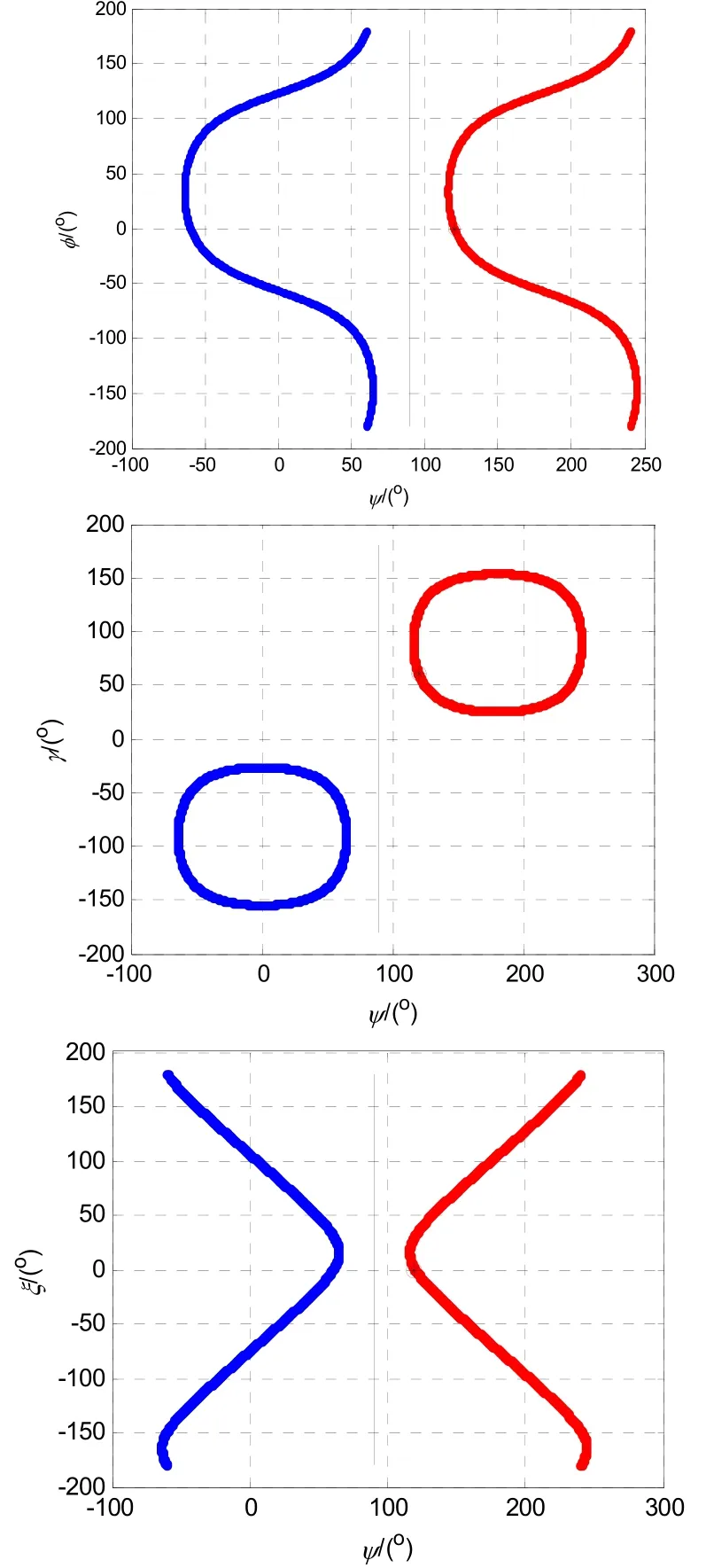
圖2 矩陣不變時的擴展克雷洛夫角Fig.2 Krylov angle when matrix is invariant

而當φ=0 °、ψ=60 °、γ=60 °、ξ=0 °時，滿足矩陣保持不變的擴展克雷洛夫角如圖3中藍色曲線和紅色曲線所示。

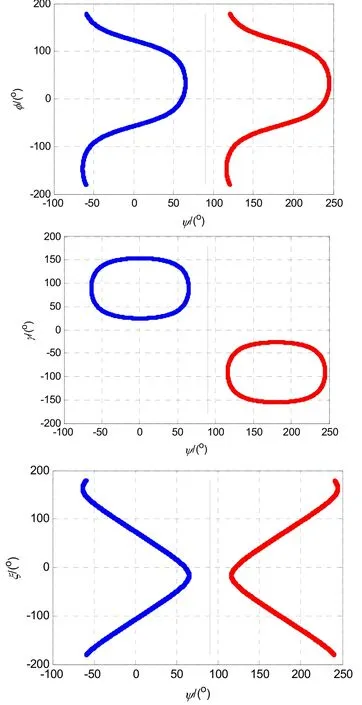
圖3 矩陣不變時的擴展克雷洛夫角Fig.3 Krylov angle when matrix is invariant

根據四次擴展克雷洛夫角的旋轉順序，寫出擴展克雷洛夫角對應的角速度方程為：

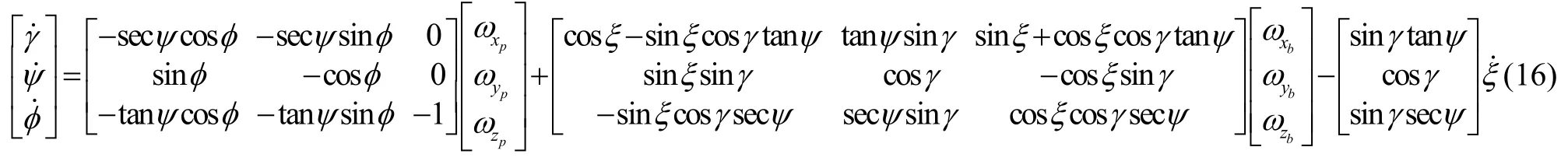
從擴展克雷洛夫角的坐標變換矩陣和角速度方程可以看出，四個角度φ、ψ、γ、ξ存在冗余，必須進行約束。

4.2 擴展克雷洛夫角因果約束方法

從擴展克雷洛夫角的坐標變換矩陣和角速度方程可以看出，必須對四個角度φ、ψ、γ、ξ進行因果約束以實現響應的唯一性。所謂的“因果約束”就是把γ角作為因變量，根據γ角所處的區間采用不同的控制策略[10,11]。具體因果約束的策略如圖4和圖5所示。

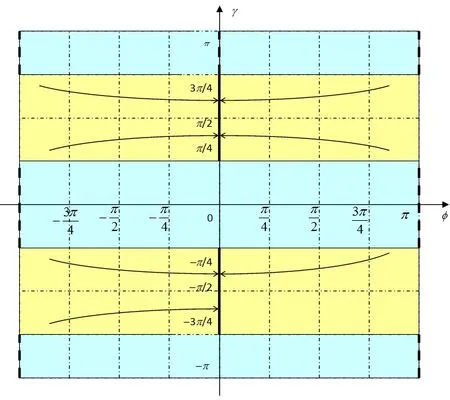
圖4 φ-γ的具體因果約束策略示意圖Fig.4 Diagram of causal constraint strategy of φ-γ

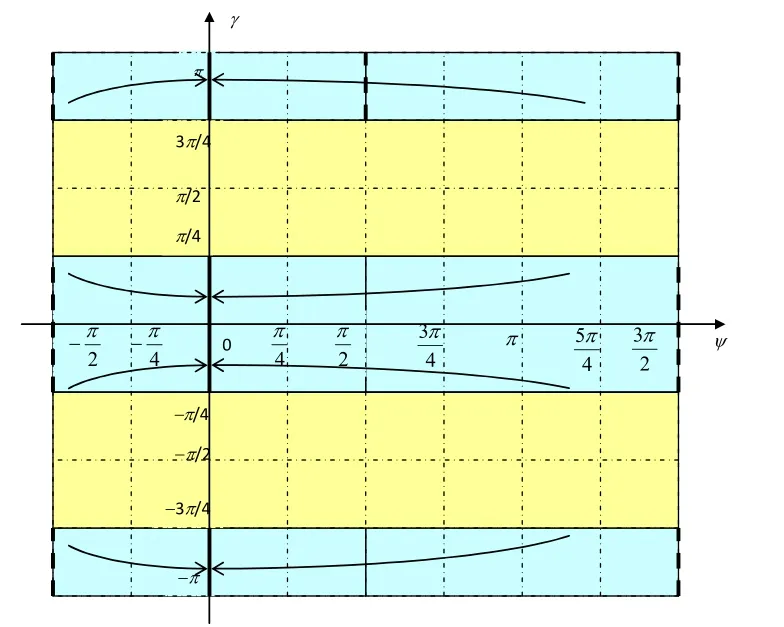
圖5 ψ-γ的具體因果約束策略示意圖Fig.5 Diagram of causal constraint strategy of ψ-γ

從圖4和圖5中可以看出，根據φ、ψ、γ所處的區間，對擴展克雷洛夫角進行因果約束。具體方法為：（1）當時

由于四個角度φ、ψ、γ、ξ的初值為隨機狀態，必須進行狀態轉移使得φ′=0，此時，ξ為：

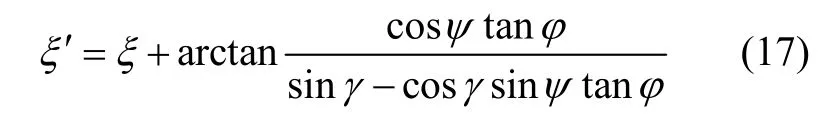
把式(17)代入式(18)，

在狀態轉移完成后，φ′= 0，ψ′、γ′、ξ′作為微分方程的初值進行姿態角ψ、γ、ξ的解算，微分方程為：

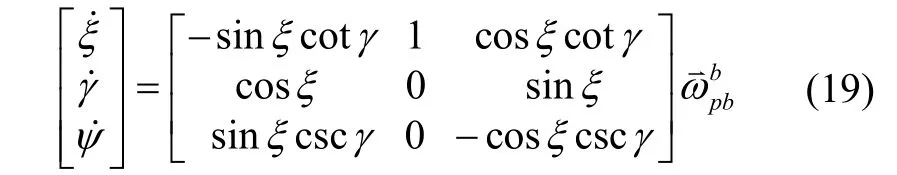
注意到，雖然cotγ、cscγ等函數在γ∈ [ -1 80°, +180°]的全局范圍內存在奇異值，但在的限制范圍內不存在奇異值。此時，坐標變換矩陣為：

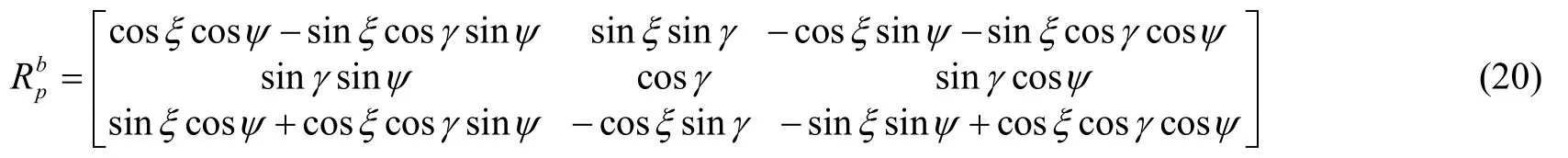
進行狀態轉移使得ψ′=0，此時，ξ′為：

把式(21)代入式(22)：

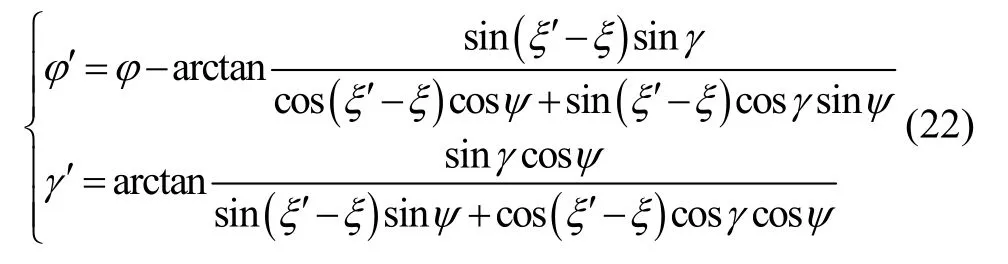
在狀態轉移完成后，ψ′=0，φ′、γ′、ξ′作為微分方程的初值進行姿態角φ、γ、ξ的解算，微分方程為：

注意到，雖然tanγ、secγ等函數在γ∈ [ -1 80°, +180°]的全局范圍內存在奇異值，但在或的限制范圍內不存在奇異值。此時，坐標變換矩陣為：

由以上分析可以看出，通過四次角度旋轉，根據γ角的范圍，進行狀態轉移使得同軸的φ′角或者ψ′=0為零，再將狀態轉移后的初值代入式(16)得到不同γ角條件下的姿態角微分方程，對其進行積分即可得到載體姿態角。而且，基于擴展克雷洛夫角的因果約束策略只與γ所處區間有關系，而與載體角運動無關，具有自主性，這是其另外一個優點。

5 試驗驗證

5.1 采用克雷洛夫角的全姿態試驗驗證

下面通過分析在大動態試驗設備（如圖6）的慣組測試數據來驗證克雷洛夫角的全姿態功能及在不同轉動順序下的導航結果。該測試設備可實現俯仰角、橫滾角的±180 °轉動，在試驗過程中繞俯仰軸共轉了3個大圈，在每一圈繞橫滾軸轉了1個大圈，下面分別為按照克雷洛夫角的兩種轉動順序進行導航解算。

圖6 大動態試驗設備Fig.6 Large dynamic test equipment

以式(4)作為姿態角更新方程，以東北天地理坐標系作為導航系進行導航解算，三個姿態角如圖7所示，作為旋轉過程中的中間角度，ψ1角工作于（-55 °, +89.3 °）區間。

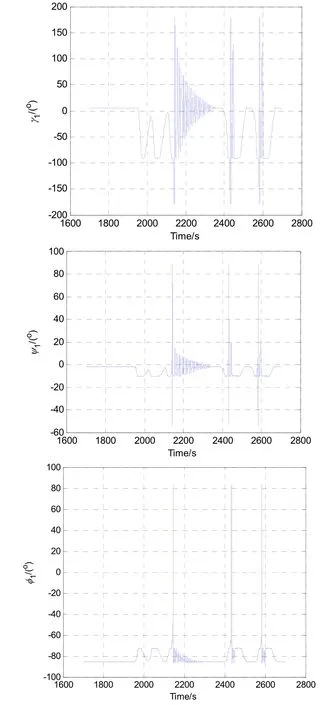
圖7 三個角度的變化過程Fig.7 Changing process of the three angles

當ψ1角接近90 °時，姿態角誤差最大（如圖8所示），γ1和φ1的瞬時角度誤差超過20 °，經過三次轉圈后ψ1角累計誤差超過0.2 °，造成位置誤差偏大的原因是離散化采樣時間引起的量化誤差。三維空間的位置如圖9所示，從圖中可以看出，位置誤差可達2000 m。

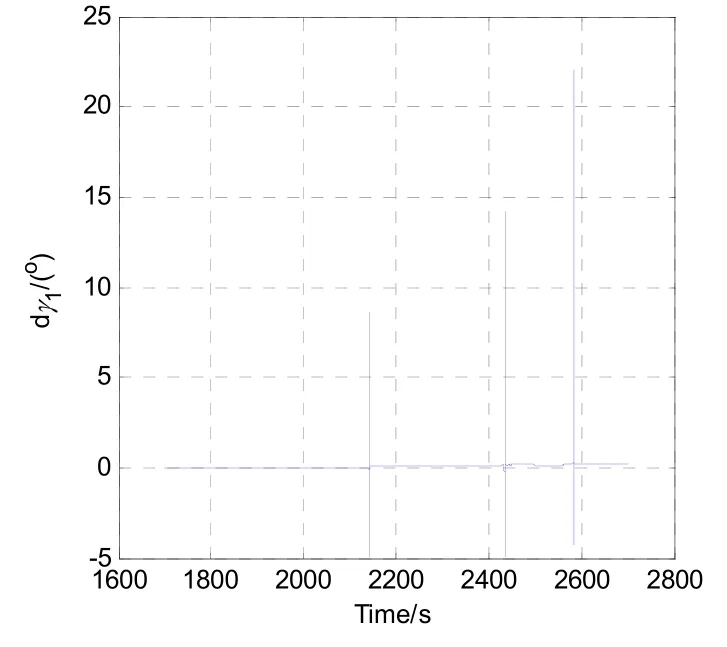
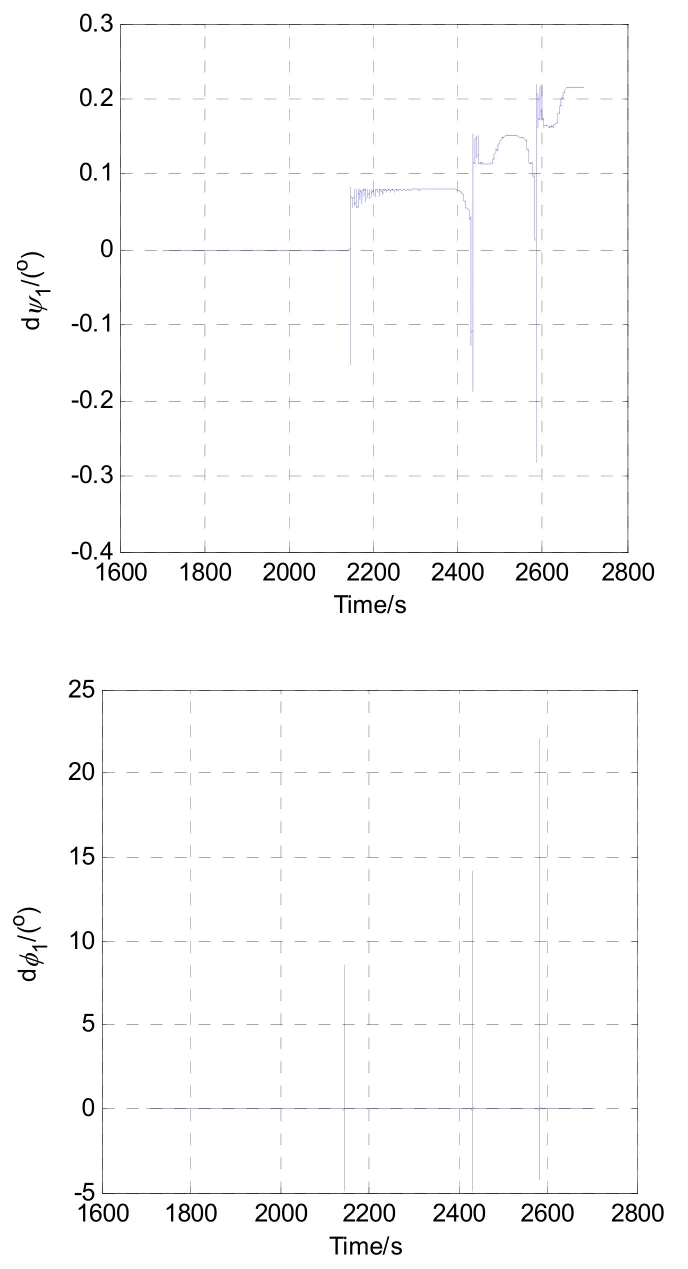
圖8 三個角度誤差的變化過程Fig.8 Changing process of the three angle errors

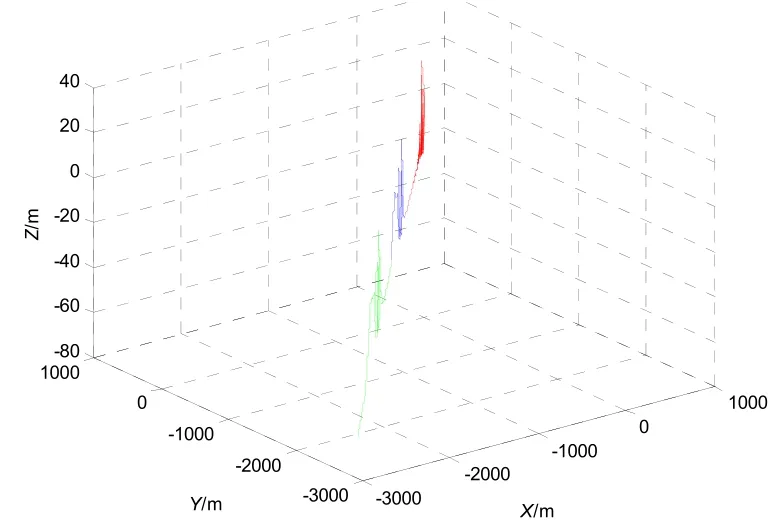
圖9 三維位置Fig.9 The three-dimensional position of the three angles

以式(6)作為姿態角更新方程，以東北天地理坐標系作為導航系進行導航解算，三個姿態角如圖10所示，作為旋轉過程中的中間角度，γ2角工作于（-81 °, +81 °）區間。

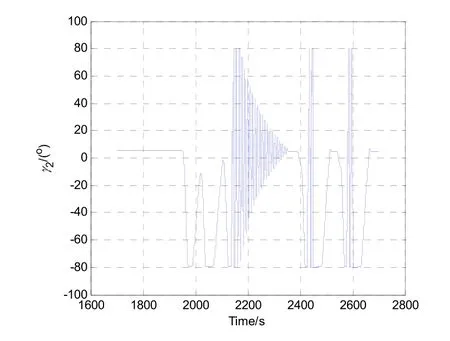
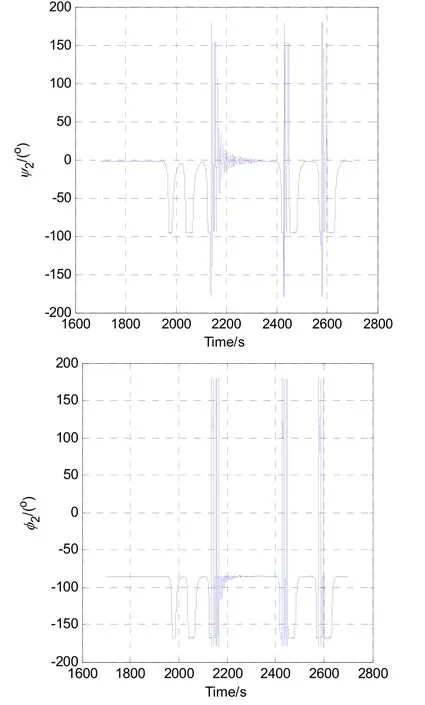
圖10 三個角度的變化過程Fig.10 Changing process of the three angles

從圖11的姿態角誤差曲線可以看出，γ2誤差小于0.005 °，ψ2和φ2角誤差為0.02 °，該誤差對導航結果的影響可忽略。三維空間的位置如圖12所示，從圖中可以看出，解算量較好地復現出在試驗設備上的運行軌跡，位置誤差約為20 m；雖然離散化采樣時間也會引起位置誤差，但該量化誤差相對圖9的位置誤差較小。

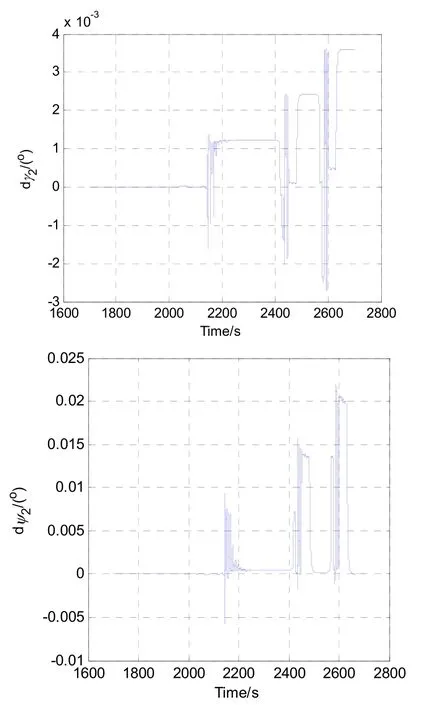
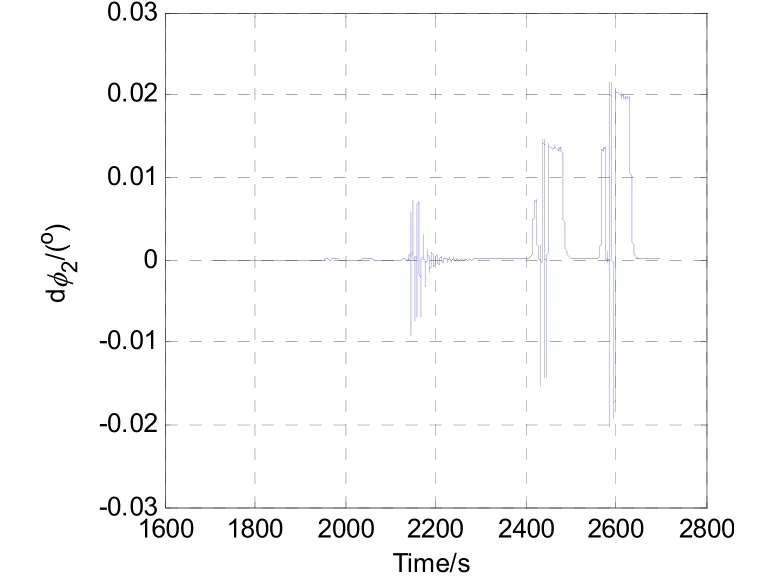
圖11 三個角度誤差的變化過程Fig.11 Changing process of the three angle errors

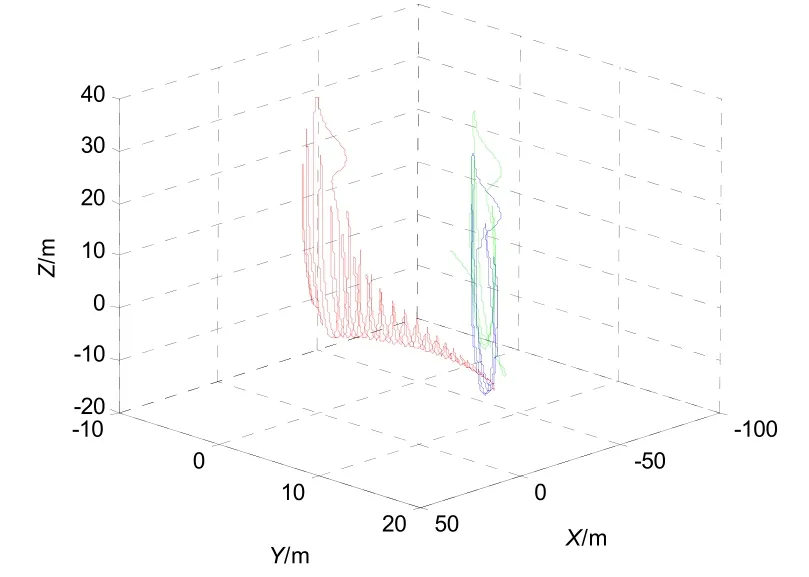
圖12 三維位置Fig.12 The three-dimensional position of the three angles

采用雙歐拉角法進行導航時可采用方法：(1) 以式(4)中的ψ1作為切換依據，當ψ1∈[-45 °, +45 °]時，對式(4)進行積分解算；否則對式(6)進行積分解算。仿真結果與圖10-12相同。(2) 以式(6)中的γ2作為切換依據，當γ2∈[-45 °, +45 °]時，對式(6)進行積分解算；否則對式(4)進行積分解算。仿真結果與圖7-9相同，這說明采用雙歐拉角法仍未從根本上解決奇異值問題。因此，需要事先根據先驗信息選取某一種特定的正反歐拉解算方法，但是在導航效果上與直接選取其中一種量化誤差相對較小的導航結果相同。

從以上導航結果可以看出，基于克雷洛夫角的姿態解算雖然可以實現全姿態導航的功能，但存在兩個問題：(1)轉動過程中的中間角度越接近90 °，引起的動態誤差會增大；(2)姿態解算精度與三次轉動順序直接相關。因此，雖然通過補償可減小中間角度接近90 °時的動態誤差，但應用過程中應通過改變旋轉順序等措施以提高使用精度。

5.2 采用擴展克雷洛夫角的全姿態試驗驗證

以5.1節的大動態試驗數據為例，采用擴展克雷洛夫角作為姿態角更新方程，導航解算的四個姿態角如圖13所示。從圖中可以看出，在1964.66 s之前，因此，ψ為0，而φ、γ、ξ按照式(23)進行姿態解算。而在1964.66 s時刻，，進行狀態轉移，從初始狀態φ=-90.0 °、ψ= 0、γ=-45.0 °、ξ=-13.1 °（如圖14中的紅色‘o’）瞬時轉移到末端狀態φ= 0 °、ψ=135.0 °、γ=90.0 °、ξ=-103.2 °（如圖14中的黑色‘*’）。在1964.66 s之后，，因此，φ為0，而ψ、γ、ξ按照式(19)進行姿態解算。

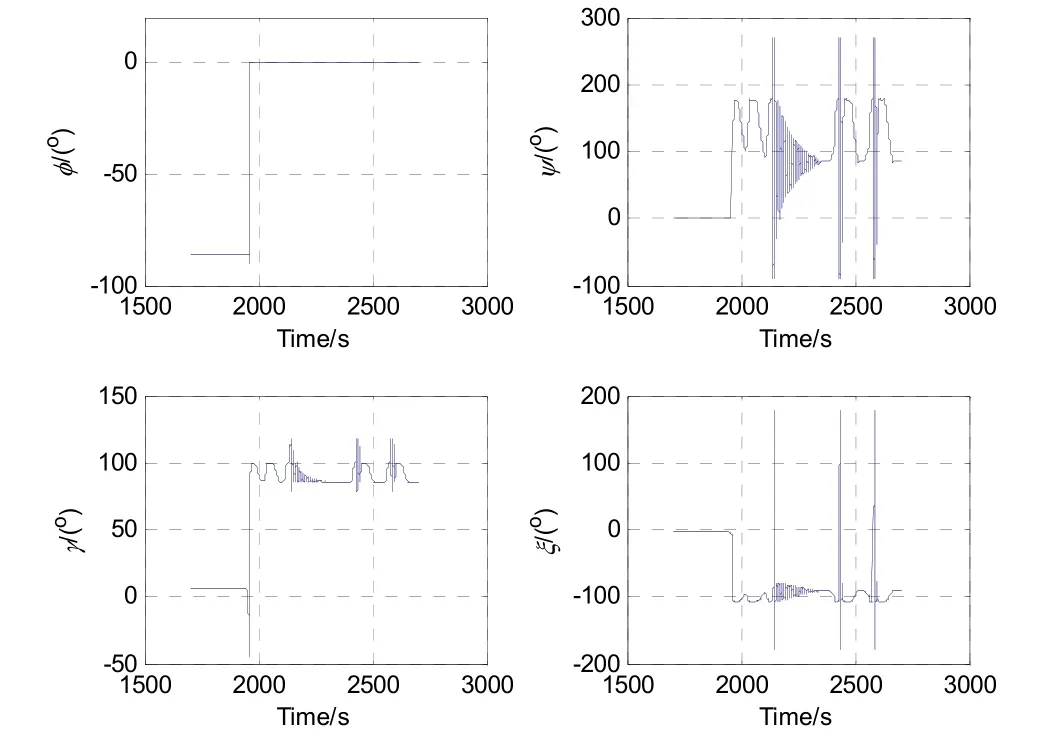
圖13 四個角度的變化過程Fig.13 Changing process of the four angle errors

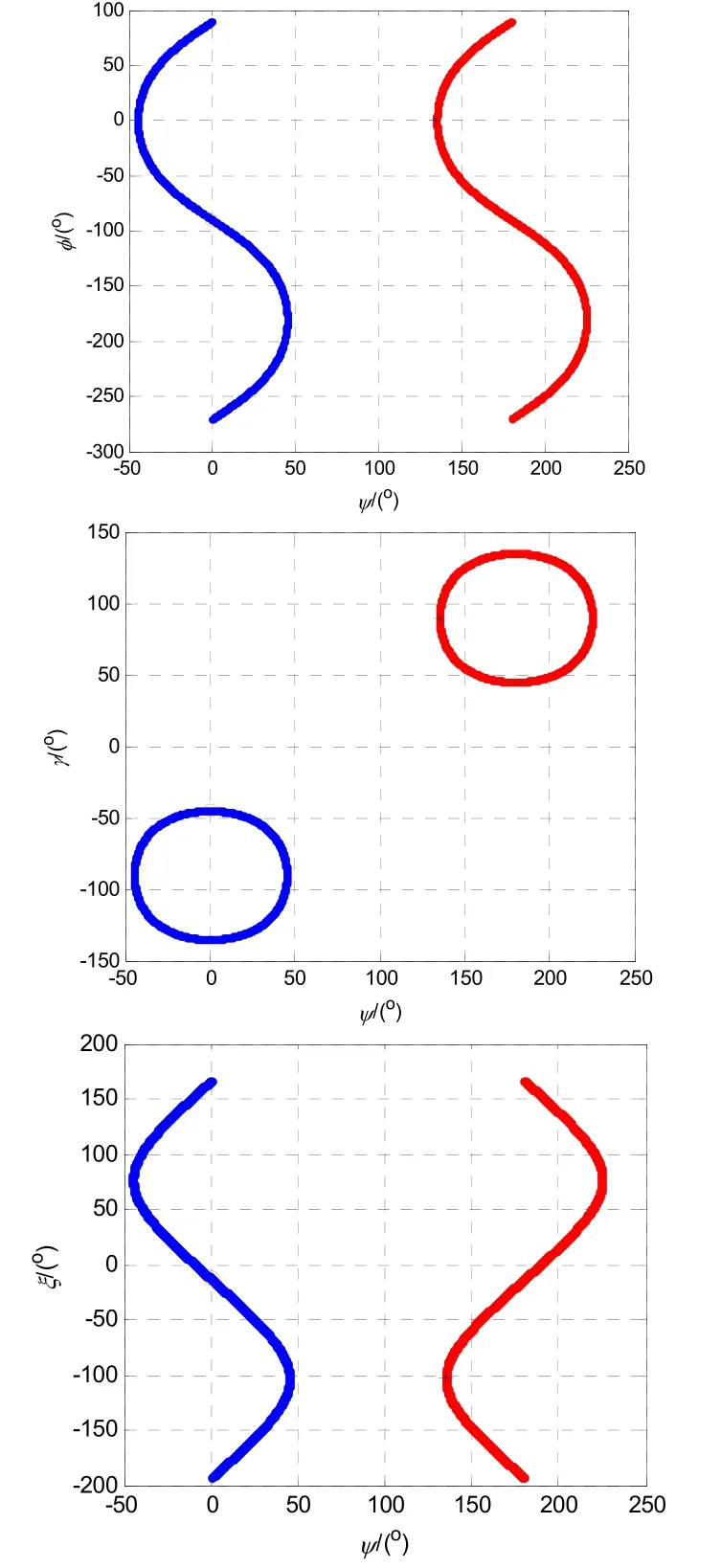
圖14 四個角度的狀態轉移示意圖Fig.14 Diagram of state transtion process of the four angle errors

四個角度的角度誤差曲線如圖15所示。

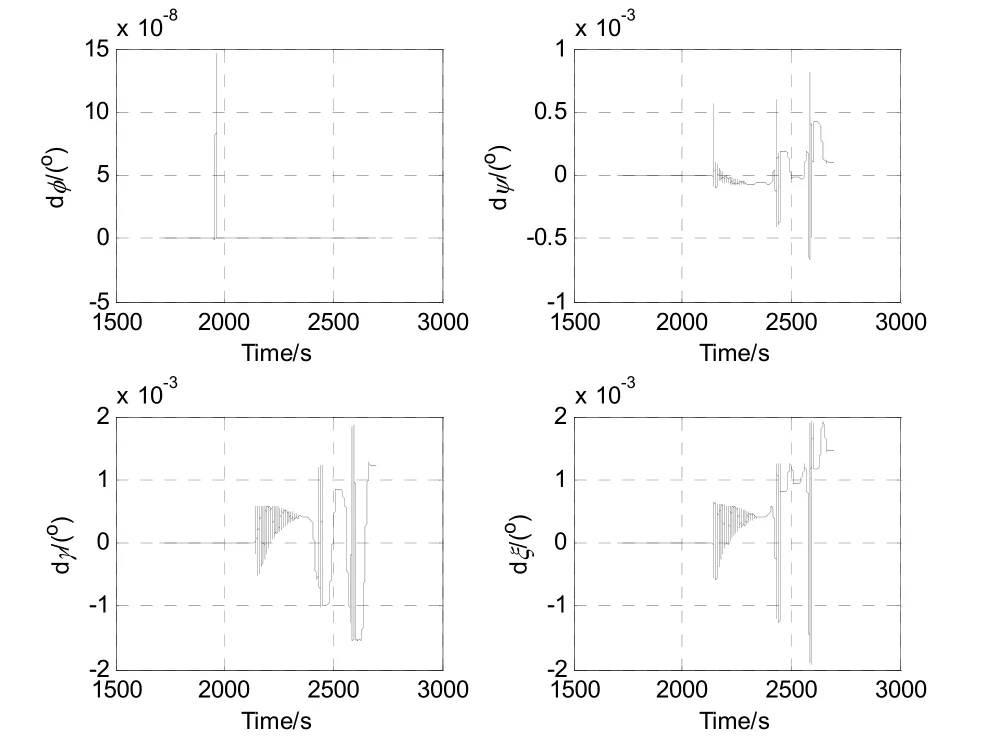
圖15 四個角度誤差的變化過程Fig.15 Changing process of the four angle errors

從圖15的姿態角誤差曲線可以看出，最大角度誤差不大于0.002°（7.2"），具備較高的精度。

對應圖4和圖5，圖16中藍色曲線為大動態試驗數據下的φ-γ、ψ-γ因果約束關系。由圖16可以看出，當時，ψ角為0 °；當時，φ角為0 °，與3.2節的因果約束策略一致。

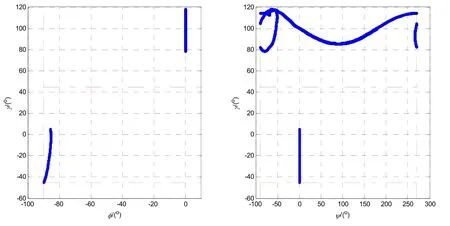
圖16 因果約束策略示意圖Fig.16 Diagram of causal constraint strategy

三維空間的位置如圖17所示。

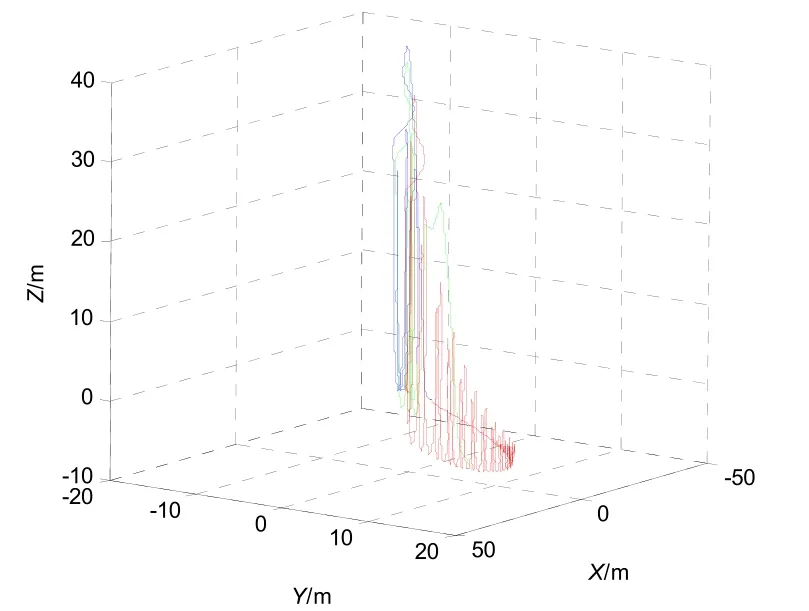
圖17 擴展克雷洛夫角參與導航解算的三維位置Fig.17 The three-dimensional position of the three angles based on extended Krylov angle

從圖17中可以看出，三維位置圖很好地復現出在試驗設備上的運行軌跡，位置誤差約為10 m，相比于克雷洛夫角法和雙歐拉法，無需通過變換或者切換不同的姿態角轉動順序即可求解得到更高的導航精度。

6 結 論

對于取消滾動控制的大機動全姿態飛行場合，基于3個克雷洛夫角描述的姿態角存在奇異值，而如果在工程上采用限定姿態角范圍將不滿足全姿態飛行使用要求。雖然雙歐拉角法為解決多值問題和奇異值問題提供了一個思路，但需要依據先驗信息判斷切換條件，兩套歐拉角并行解算的計算量較大，且仍沒從根本上解決奇異值問題。本文提出的基于擴展克雷洛夫角的全姿態導航解算方法，在導航過程中不會發生奇異現象，具備全姿態高精度導航能力，綜合仿真及試驗數據驗證結果表明，基于四次旋轉的擴展克雷洛夫角的姿態解算方法可完全滿足載體大機動全姿態運動的需求。