一種單偏振低噪聲諧振式空芯光子晶體光纖陀螺

申河良，畢 然，傅 力，佘 玄，陳 侃，舒曉武

（1. 浙江大學光電科學與工程學院，杭州 310027；2. 光迅科技股份有限公司，武漢 430205）

近年來，隨著各種海陸空天慣導航姿系統的發展，對慣性器件在輕型微小化、高集成度、測量精度等方面提出越來越高的要求。諧振式光纖陀螺（Resonator Fiber Optic Gyro, RFOG）通過檢測光纖諧振環中順逆兩個方向的諧振頻率差來測量角速度。在同等精度下，RFOG所需光纖長度相較于干涉式光纖陀螺可以縮短1-2個數量級。在集成化、小型化、高精度等方面具有優勢，是陀螺未來發展的重要方向[1]。光纖諧振腔是RFOG的主要敏感組件，其性能直接影響陀螺精度提升。目前諧振腔多采用傳統的實芯光纖繞制，環境溫度適應性差，寄生噪聲較大，限制了RFOG的精度。空芯光子晶體光纖（Hollow Core Photonic Crystal Fiber,HCPCF）的出現，為RFOG的發展提供了新方向[2]，HCPCF利用周期性結構使得傳播光束95%以上的能量位于中央空氣中，可大大降低克爾效應、背向散射、溫度效應等寄生誤差，并且其彎曲損耗小，有利于小型化[3-5]。因此諧振式空芯光子晶體光纖陀螺（HC-RFOG）受到了國內外各研究單位的重點關注。但由于缺少成熟的空芯光子晶體光纖耦合器，限制了RFOG中HCPCF的應用。目前解決這一問題主要有基于熔接型和空間光路耦合型兩種方案。

基于熔接耦合的諧振腔有穩定性較好的優點，如浙江大學馬慧蓮教授課題組采用將HCPCF與傳統保偏光纖直接熔接，制作了混合型光纖諧振腔[6]，但HCPCF內部含有空氣孔，傳統的高溫熔接會造成空氣孔塌陷導致熔接損耗過大，最終清晰度僅為6.67。

基于空間光路耦合的方案又可分為基于準直系統耦合、硅基自由空間耦合、光波導端面對準耦合三種技術路線。基于準直系統耦合最早由Honeywell提出[3]，其耦合器是由分光片構成的空間耦合結構，HCPCF諧振腔的清晰度達到了42。國內最早由北航搭建并制作陀螺樣機，后來發展為采用一對準直器和一系列偏振相關器件構成微光學偏振耦合器，實現了一體化的HCPCF諧振腔[7]，其余如法國Paris-Saclay大學[8]，北京航天時代光電技術有限公司[9]均采用該方法搭建諧振腔。基于準直系統的耦合結構由于采用分立器件，體積較大，穩定性較低，但其優勢在于低損耗的耦合可以使諧振腔達到較高的清晰度。

硅基自由空間耦合首先由Honeywell公司提出，其使用高度集成的自由空間硅光學平臺來實現腔內光波的低損耗循環和光信號的有效耦合進腔，據報道，該諧振腔的清晰度可達35[10]。此外，采用微加工技術可以將透鏡、分束器、偏振器等元件集成在一個硅基平臺上，大大提升了系統集成度，但該方案對微納加工和裝配等工藝提出了較高要求。

光波導端面對準耦合最早被斯坦福大學研究人員采用，他們利用微位移機械平臺將HCPCF與單模光纖耦合器尾纖進行端面對準耦合，成功搭建了HC-RFOG系統[11]。該方法簡單易行，但由于不同光纖之間模場不匹配，導致每個端口的耦合損耗高達2.1 dB。2017年，浙江大學馬慧蓮教授課題組采用二氧化硅波導耦合器與傳統光纖直接對接的方式，搭建了清晰度高達196.7的無熔接點諧振腔[12]，之后他們又報道，該型諧振腔清晰度可以提高到1324[13]，展現了該方案巨大的應用潛力。

受以上各方案的啟發，本文提出了一種單偏振低噪聲的空芯光子晶體光纖諧振腔，其主要由HCPCF環與退火質子交換鈮酸鋰（APE-LN）波導耦合器通過端面對準耦合的方式搭建而成。由于傳統APE-LN出射光斑分布不對稱，因此其與光纖對準時耦合損耗較大（約1 dB）。針對此問題，本文提出利用離子注入和鍵合技術[14]在APE-LN波導的上表面覆蓋一層鈮酸鋰（LN）材料，從而對APE-LN出射光斑進行改善。通過仿真計算，求得了模斑改善前后的APE-LN波導與HCPCF和傳統實芯光纖的耦合效率，給出了該諧振腔的理論極限靈敏度，對HC-RFOG的研究具有一定的參考意義。

1 單偏振低噪聲空芯光纖諧振腔的諧振理論

圖1為基于HCPCF的單偏振諧振腔結構，耦合端口2與耦合端口3分別與HCPCF環的兩端連接，通過端面對準耦合方式與耦合器形成封閉回路，從而形成HCPCF諧振環。耦合端口1和耦合端口2分別連接兩根輸入實芯光纖1、2，從而保證光波的輸入/輸出諧振環。

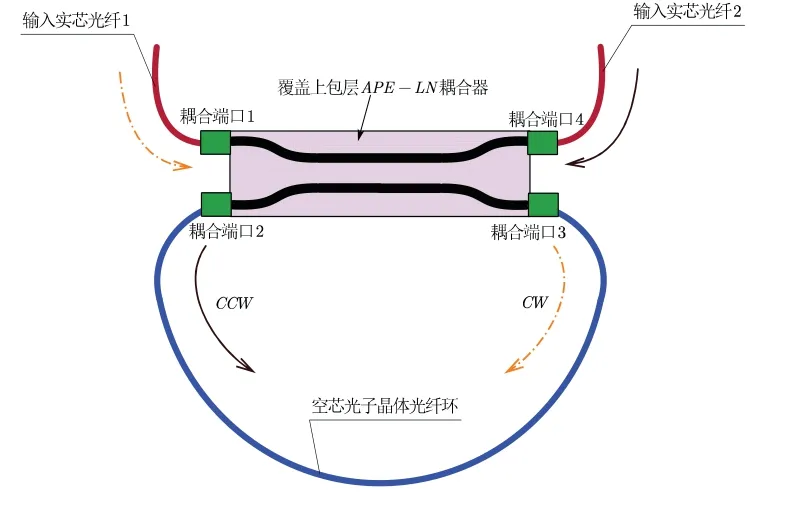
圖1 單偏振低噪聲空芯光子晶體光纖諧振腔示意圖Fig.1 Schematic diagram of the single polarization and low noise HCPCF resonator

圖1也顯示了該諧振腔的工作原理，以順時針（Clock Wise, CW）方向傳輸光波為例，輸入實芯光纖1發出光束，經過耦合端口1進入耦合器，采用成熟的退火質子交換工藝制作的LN波導具有極高的消光比（＞60 dB）足以保證腔內光波偏振態保持單一穩定。然后，光波通過耦合端口3進入HCPCF環中。光波沿CW方向在諧振環中傳播，經過耦合端口2又進入耦合器，并分為兩部分，一部分光波重新經過耦合端口3進入諧振腔，另一部分光波經過耦合端口4輸出，如此循環，多次傳輸后的CW光波被探測器接收。若從耦合端口1入射的光波為：

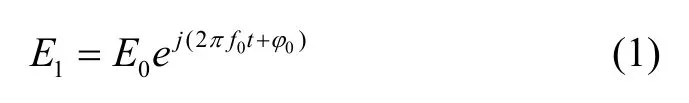
其中，E0為輸入光波光振幅，f0為光源的中心頻率，φ0為光源的初始相位。通過光場疊加理論，可以得到：

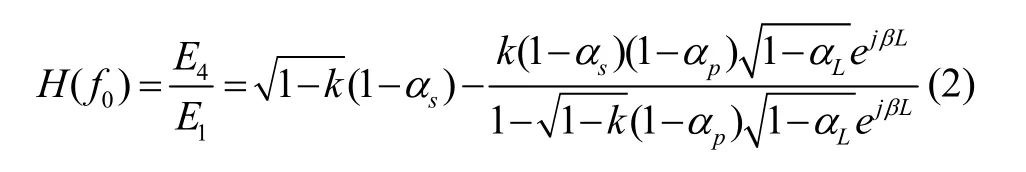
其中，L為光纖環長，k為耦合器的耦合系數，αs為實芯光纖與波導端面對準耦合損耗，αp為實芯光纖與波導端面對準耦合損耗，αL為空芯光纖傳輸損耗。β=neff2πf0/c為傳播常數，其中neff為纖芯等效折射率，c為真空中光速。若設L=10 m，k= 0.1，αs= 0.5 dB，αp= 0.5 dB，αL=20 dB/km，neff= 1則可給出諧振腔輸出光強隨入射光波頻率的變化曲線，如圖2(a)所示。

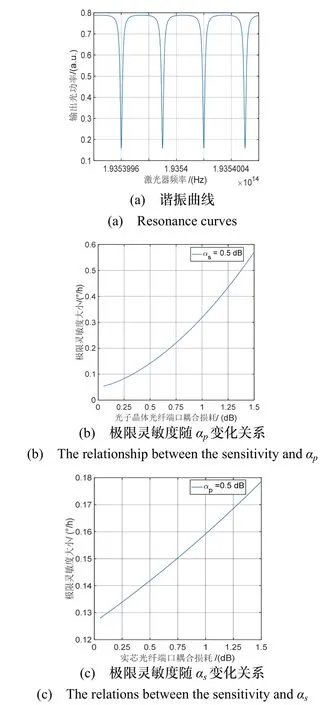
圖2 單偏振低噪聲空芯光纖諧振腔理論分析Fig.2 Theoretical analysis of the single polarization and low noise HCPCF resonator

對RFOG系統而言，諧振腔的極限靈敏度是極為重要的參數，其表達式為[15]：

其中，A為光纖環面積，λ0為波長，Г為諧振曲線的半高全寬，D為諧振環的直徑，F為諧振腔的清晰度，SNR為系統信噪比，由探測器散粒噪聲決定的SNR可以表示為：

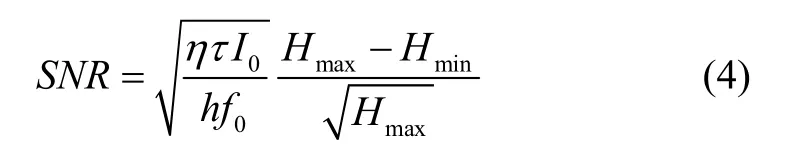
其中，η為光探測器的量子效率，τ為探測器積分時間，I0為輸入光功率，h為普朗克常數，Hmax、Hmin分別為諧振曲線的最大值和最小值。

結合理論極限靈敏度表達式(3)，可以分析不同耦合端口的損耗對陀螺性能的影響。若設αs=0.5 dB，λ0=1550 nm，I0=1 mW，D=10 cm，η=0.85，τ=1 s，其余參數與上文一致，空芯光子晶體光纖與波導的耦合損耗αp從0.05 dB增加到1.5 dB時，極限靈敏度變化如圖2(b)所示，從計算結果可以看出，極限靈敏度從0.0542 °/h增大到了0.5709 °/h，變化量約為初始值的10倍。相對而言，若設αp=0.5 dB，其余參數保持不變，實芯光纖與波導的耦合損耗αs從0.05 dB增加到1.5 dB時，計算結果如圖2(c)所示，極限靈敏度僅從 0.1279 °/h 增大到了 0.1786 °/h，僅增加了0.0507 °/h。以上結果表明，在光纖傳輸損耗固定的情況下，該諧振腔的極限靈敏度主要由空芯光子晶體光纖與波導的端面對準耦合損耗αp決定，這為下一步諧振腔的設計和參數優化提供了指導。

2 單偏振低噪聲空芯光纖諧振腔設計與分析

2.1 覆蓋LN上包層的APE-LN建模

降低諧振腔的耦合損耗，從而提升RFOG的性能是本文工作的重點。在光纖與波導理想準直的情況下，影響最大的是模場失配損耗，其次是菲涅爾反射損耗，其中菲涅爾反射損耗可以利用增透膜來降低。最難解決的問題就是如何改善兩個模場的失配。耦合效率ξ與模場匹配的關系可以用光纖與波導模場分布的重疊積分來表示[16]：

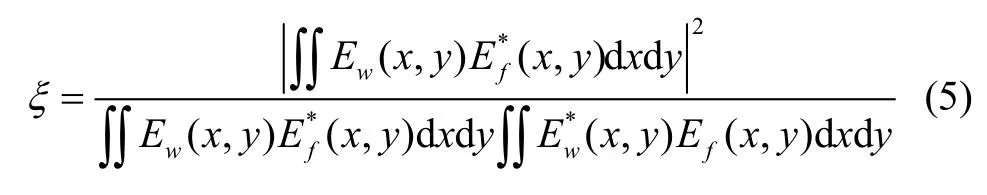
式中Ew表示波導模場，Ef表示光纖模場。對于均勻單模光纖（SMF）而言，其基模光場在光纖橫截面上呈現為類高斯分布，如圖3(a)所示。而APE-LN波導的折射率分布并不對稱，其OXZ波導折射率分布截面如圖3(b)所示。其中綠色區域為質子交換區域，寬度為w，擴散深度為hx，折射率差Δn為擴散源沿軸向晶體內部擴散得到的表面（最大）折射率增量，n0為鈮酸鋰襯底的折射率。

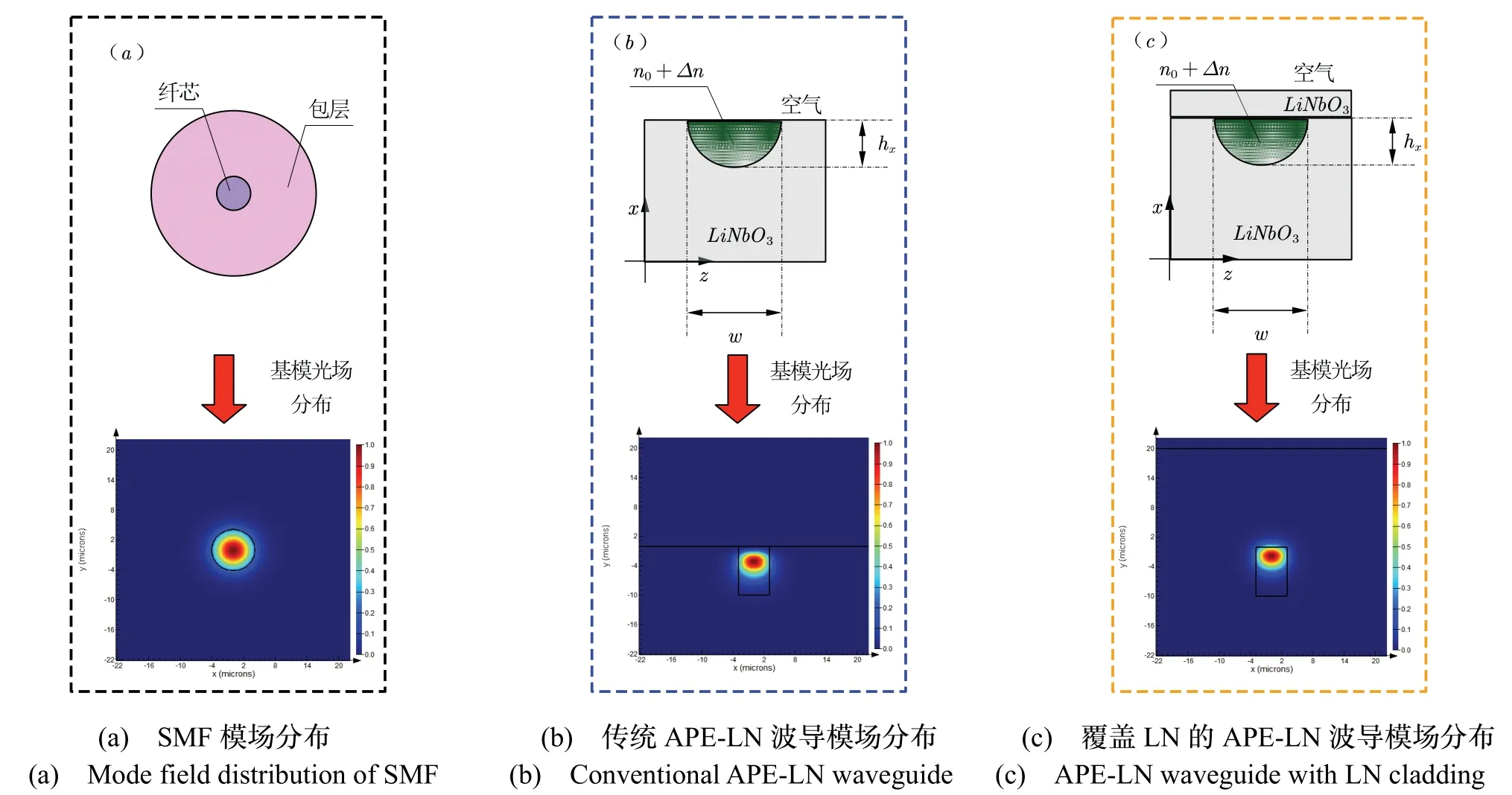
圖3 波導結構與模場分布Fig.3 Waveguide structures and mode field distributions

對于x切鈮酸鋰材料，質子交換形成的光波導折射率表達式為：

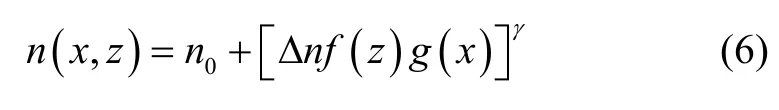
其中，g(x)為x方向上的折射率分布，f(z)為沿z方向的分布由函數，γ為擴散型折射率的指數冪。x方向上的折射率分布由函數g(x)為高斯型，其表達式為:

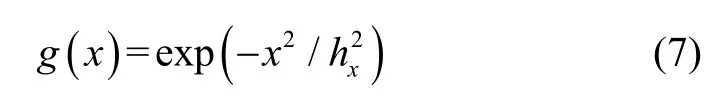
其中，hx為質子源擴散深度的1/e，hz為z方向上的擴散寬度，γ=hz/hx為擴散比。沿z方向的折射率分布函數f(z)為誤差函數型，其表達式為：

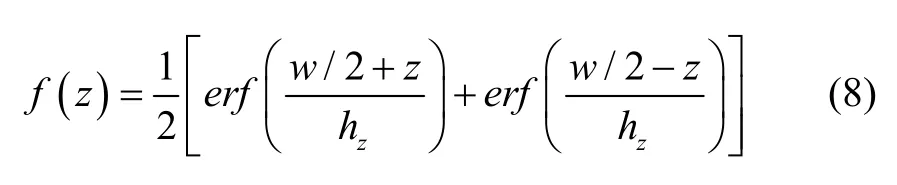
其中w為z方向上擴散源的寬度。利用基于時域有限差分法的FDTD solutions光學仿真軟件可以得到其模場分布，如圖3(b)所示，根據仿真結果可知，其基模光場縱向分布不對稱，根據上文分析，這將會產生較大的光纖-波導耦合損耗。

針對這一問題，本文提出在APE-LN波導上方覆蓋一層LN材料的方法來改善模場分布不對稱的方法，如圖3(c)所示，利用離子注入和鍵合技術[14]在APE-LN波導表面覆蓋一層LN材料，以此來改變APE-LN波導上表面的折射率分布，使得波導出射的光斑變為對稱分布，從而達到減小耦合損耗的目的。導基模模場分布的改善情況，在保證單模傳輸的前提下，挑選了一組質子交換鈮酸鋰波導參數（w=6.0 μm,hx=5.5 μm,Δn=0.011），利用FDTD solutions仿真得到了模場縱向分布的變化情況。圖4(a)展示了在1550 nm處，APE-LN的基模模場分布，沿圖中紅色箭頭所示方向考察其截面，則可得到如圖4(b)所示的模場縱向分布曲線，可以清晰地看到其呈現非對稱形狀，在圖中y＜ 0 μm的方向上，呈指數型衰減，在y= 0 μm處模場分布戛然而止。作為對比，圖4(c)(d)則展示了在上表面覆蓋LN材料后，模場縱向分布在y= 0 μm兩側呈現對稱分布，初步印證本方法可行性。

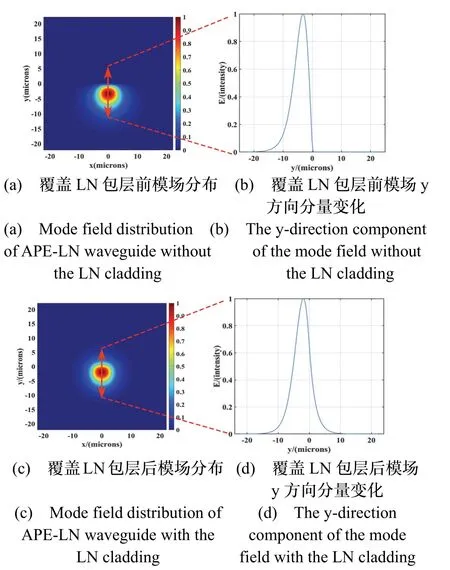
圖4 APE-LN波導模場分布變化情況Fig.4 Mode field distribution of APE-LN waveguide mode為更加直觀地考察覆蓋LN層前后，APE-LN波

2.2 空芯光子晶體光纖的建模

如上文所述，該諧振腔的構建需要信號光從波導有效耦合到實芯光纖和空芯光子晶體光纖中，因此建立實芯光纖與空芯光子晶體光纖的模型，對理論仿真至關重要。對于實芯光纖的模型采用常見的SMF-28光纖，其基模模場分布如圖3(a)所示，由于其建模方法已經非常成熟，這里就不再贅述。接下來，主要進行空芯光子晶體光纖的建模仿真。在FDTD solutions中建立空芯光子晶體光纖的二維橫截面結構模型，對標物為圖5(a)所示的NKT公司的商用7芯光子晶體光纖NKT-1550-02。

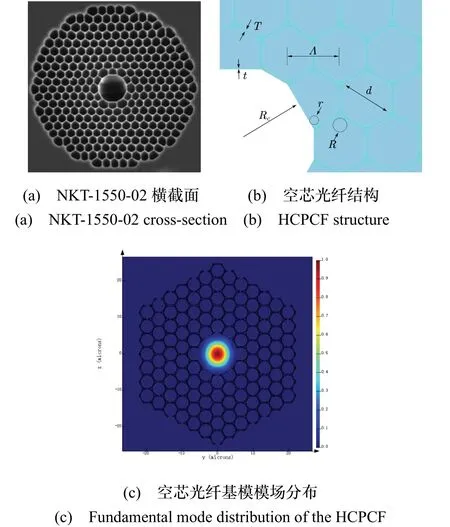
圖5 空芯光子晶體光纖的設計Fig.5 Design of the HCPCF

經過多輪優化仿真，綜合對光子帶隙光纖的光子帶隙設計、損耗特性研究，最終確定了光纖結構的參數設計結果，如圖5(b)所示，其中R= 1 μm，T= 100 nm分別代表毛細管的內切圓半徑和兩毛細管間壁面厚度，r= 0.35 μm，t= 30 nm分別代表五邊形底邊的內切圓半徑和壁面厚度，Λ= 3.8 μm代表毛細管周期間距，d= 3.84 μm代表毛細管內徑，Rc= 5.71 μm代表纖芯半徑。設定參數后求解，在波長為1550 nm的情況下，得到如圖5(c)所示的纖芯基模模場分布。最終選擇該光斑作為目標光斑。

2.3 耦合效率仿真計算

將仿真得到的HCPCF模場分布與SMF光纖模場分布導入FDTD solutions中，與覆蓋LN上包層的APE-LN波導進行耦合效率仿真計算。為了模擬APE-LN波導上包層為LN材料，設置整個求解空間的背景材料為LN。

通過計算波導出射光斑與光纖光斑的重疊積分，可以得到在不考慮菲涅爾反射情況下的耦合效率。經過多輪參數優化，最終得到APE-LN波導在線寬w=7.0 μm，擴散深度hx=6.0 μm情況下，其出射光斑與光纖光斑耦合效率最高。圖6(a)展示了APE-LN波導在w=7.0 μm，hx=6.0 μm時，與HCPCF的耦合效率隨Δn的變化情況，其中虛線表示APE-LN波導在沒有覆蓋LN包層時耦合效率的變化趨勢。可以看出，隨著Δn的不斷增大，可以將APE-LN波導與HCPCF的耦合效率從0.8239提升到0.8937，在Δn= 0.014時達到最大，然后開始減小。實線表示覆蓋LN上包層后APE-LN波導與HCPCF的耦合效率變化趨勢，其變化也是隨著Δn的增大，先增大后減小，在Δn= 0.016時達到最大為0.9114。通過對比兩條曲線，可以明顯看出，覆蓋上包層的APE-LN波導與HCPCF耦合效率普遍更高，再次印證了覆蓋LN材料對APE-LN出射光斑的改善作用。

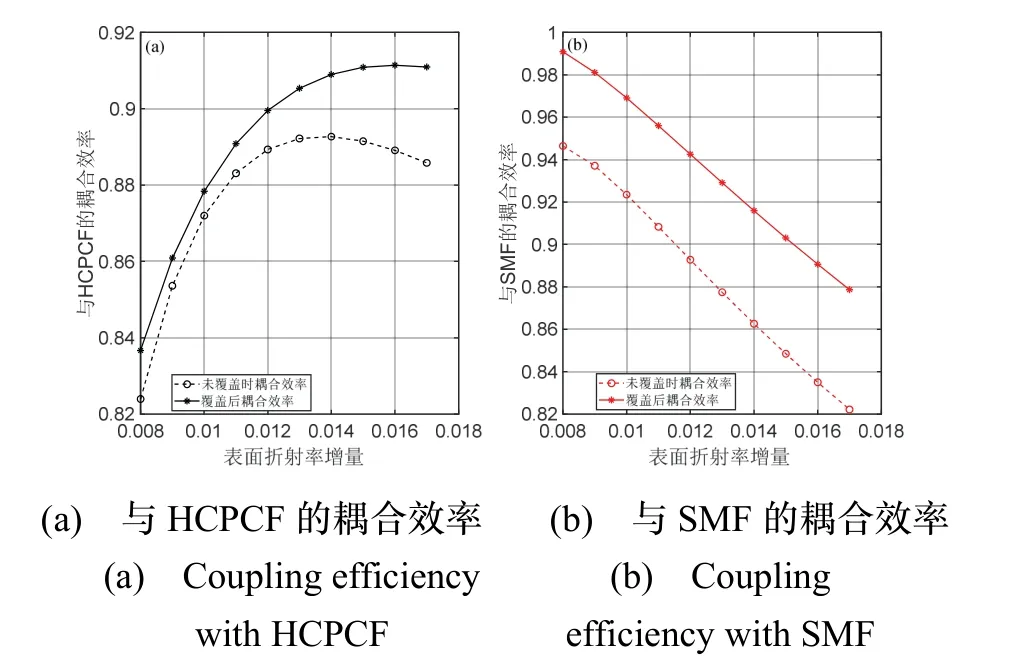
圖6 APE-LN波導與光纖耦合效率的仿真優化Fig.6 Simulation optimization of the coupling efficiency between APE-LN waveguide and fiber

圖6(b)展示了APE-LN波導在w= 7.0 μm，hx= 6.0 μm時，與SMF的耦合效率隨Δn的變化情況。首先，通過覆蓋LN上包層前后的曲線對比，可以看出，覆蓋上包層后APE-LN波導相比于未覆蓋的APE-LN波導而言，與SMF耦合效率更高，表明覆蓋LN上包層對APE-LN波導與普通單模光纖的耦合效率也有提升作用。其次，可以看出，隨著Δn的增大，APE-LN波導與SMF的耦合效率不斷降低，與圖6(a)的變化趨勢剛好相反。這表明在選擇波導參數時，需要在兩個耦合損耗之間尋求平衡。根據上文分析結果，HCPCF與波導的耦合損耗對諧振腔性能影響更大，因此優先考慮提高與HCPCF的耦合效率，同時兼顧與SMF的耦合損耗。最終選擇參數為w= 7.0 μm，hx= 6.0 μm，Δn= 0.015，此時，與HCPCF的耦合效率為0.9109，與SMF的耦合效率為0.9031。

由于實際的LN上包層覆蓋的厚度是有限的，不會如上文仿真設置的無窮大厚度，因此需要考慮在加工時，覆蓋的LN層厚度變化對APE-LN的出射光斑改善的影響，從而尋求一個最合適的覆蓋厚度。在上文參數給定的情況下，最終的仿真結果如圖7所示，隨著覆蓋LN層厚度的增大，APE-LN波導與兩種光纖的耦合效率均是先增大后趨于平緩。其中與HCPCF的耦合效率在覆蓋厚度為3 μm時達到最大為0.9152，較之前理想化的仿真結果0.9109有所提升，而后隨著覆蓋厚度的增加而減小，最終保持不變。該結果表明實際加工中可以通過調整工藝參數進一步提升與HCPCF的耦合效率。與SMF光斑的耦合效率在覆蓋厚度為12 μm時達到最大為0.9031，此后趨于不變。根據以上仿真結果，本文選定上包層的覆蓋厚度為3 μm，此時，與HCPCF的耦合效率為0.9152，與SMF的耦合效率為0.8847。

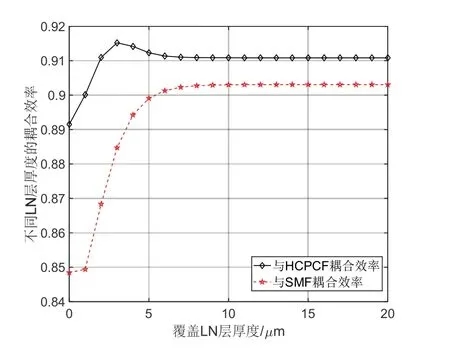
圖7 覆蓋LN層厚度不同導致的耦合效率變化Fig.7 The relationship between the coupling efficiency and thickness of the LN cladding

由于鍵合技術對材料的表面平整度有要求，所以在實際加工時，需要先對APE-LN上表面進行化學機械拋光，而后將上包層LN材料與下方APE-LN材料相對粘合，通過退火使其牢牢粘住。為分析拋光時磨去的APE-LN上表面厚度對最終耦合效率的影響，本文進行了仿真分析。分析結果如圖8所示，磨去厚度在0到500 nm不斷增加時，覆蓋3 μm LN層的APE-LN波導與HCPCF的耦合效率隨之不斷減小；相反的，與SMF的耦合效率卻隨之不斷增加。因此，在實際加工時應盡量減小APE-LN上表面被磨去的厚度，以保證腔內耦合損耗最低。若選擇磨去厚度為100 nm，則最終得到實際加工出來的覆蓋上包層APE-LN波導與HCPCF耦合效率為0.9147（耦合損耗約0.39 dB），與SMF的耦合效率為0.8852（耦合損耗約0.53 dB）。

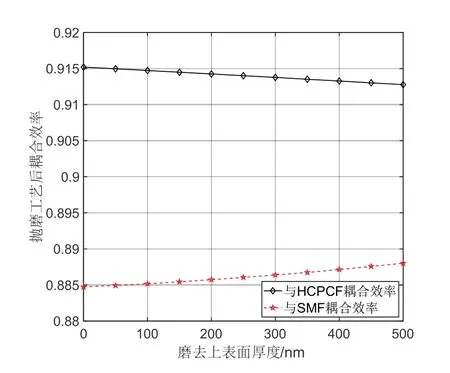
圖8 磨去波導上表面的厚度對耦合效率的影響Fig.8 Influence of the thickness of the polished waveguide upper surface on the coupling efficiency

2.4 諧振腔性能分析

根據仿真得到的耦合損耗：αs=0.53 dB，αp= 0.39 dB，并結合RFOG的理論極限靈敏度表達式(3)與第2節中諧振腔的其他參數，可以得出該條件下陀螺的極限靈敏度為0.114 °/h，達到了戰術級應用要求。且該方案諧振腔由APE-LN波導和HCPCF構成，具有小體積，抑制偏振波動、光克爾噪聲等優勢，有一定的應用前景。

3 結 論

本文提出，通過端面對準耦合的方式，可以將HCPCF環與APE-LN波導耦合器進行有效連接，從而構成一種具有單偏振低噪聲特性的HCPCF諧振腔。針對傳統APE-LN波導與光纖對準耦合損耗較大的問題，提出了使用離子注入和鍵合技術在波導上表面覆蓋一層LN材料作為上包層，從而對APE-LN波導模場分布進行改善，利用時域有限差分數值分析方法建立波導和光纖的模型，根據模場匹配模型對耦合效率進行了仿真分析，探討了波導結構、工藝參數的影響，經過優化設計，可以將HCPCF與波導的耦合損耗減小至0.39 dB，陀螺精度提升至0.114 °/h。本文對HC-RFOG的諧振腔設計有一定的參考意義。下一步可以通過繼續優化空芯光子晶體光纖的模型，構建與實際空芯光纖模場更加接近的目標光斑，從而提高仿真的準確性。此外，繼續對APE-LN波導進行優化設計與模斑改善，不斷降低光纖與波導的端面對準耦合損耗，不斷提高該方案諧振腔的性能，為構建單偏振、低噪聲、易裝配、小體積的高性能諧振式空芯光子晶體光纖陀螺打下堅實基礎。