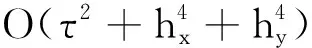二維非穩態對流擴散方程的高階緊致差分格式

魏劍英，王燕，葛永斌

寧夏大學 數學統計學院，銀川 750021

非穩態對流擴散方程是一類基本的發展方程，在生態環境、流體力學、生物數學等領域都有廣泛應用．由于解析解通常很難求出，因此，研究各種有效實用的數值方法對此類方程進行求解就顯得極為重要。

有關非穩態對流擴散方程的有限差分法的文獻報道已有很多，如文獻[1]利用半離散法和Padé逼近，推導了一維方程的截斷誤差為O(τ5+h4)的隱格式，且是無條件穩定的； 文獻[2]利用Taylor級數展開和待定系數法構造了一致四階緊致格式并結合三階TVD-Runge-Kutta方法求解了一維方程； 文獻[3]針對二維方程，對空間導數項和時間導數項分別采用四階離散和加權平均的方法，推導出一種截斷誤差為O(τ2+h4)的格式； 文獻[4]采用半離散的方法，從一維定常問題出發，利用四階緊致差分算子和Crank-Nicolson(C-N)格式，推導了一種求解二維常系數非穩態對流擴散方程的差分格式，截斷誤差為O(τ2+h4)，且是無條件穩定的； 文獻[5]針對此類方程，構造了有理型緊致交替方向隱式(ADI)格式，截斷誤差為O(τ2+h4)，且是無條件穩定的； 文獻[6]還提出了該方程無條件穩定的指數型緊致ADI差分格式，其截斷誤差依然為O(τ2+h4)； 文獻[7]利用指數變換消除對流項后轉化為擴散方程，再利用緊致公式和擴展的Simpson公式構造了一維方程的高階格式，截斷誤差為O(τ4+h4)，且是無條件穩定的； 文獻[8]針對二維非穩態常系數方程，空間方向直接采用六階組合緊致差分公式進行計算，時間方向用C-N格式離散，所提格式的截斷誤差為O(τ2+h6)，盡管該格式空間達到了六階精度，但是由于其時間只有二階精度，因此為了保證空間精度達到六階，其計算所需要采取的時間步長必須為O(h3)，即必須采用較小的時間步長，并且該方法僅適用于常系數問題。

本文針對二維非穩態變系數對流擴散方程，首先對空間二階導數采用一階導數的四階逼近公式，而一階導數采用四階Padé逼近，時間項采用二階向后差分公式(BDF)，得到一個時間二階、空間四階精度的緊致差分格式； 然后利用Taylor級數展開，對一階和二階空間導數項采用六階緊致差分公式，時間項采用三階BDF得到一個時間三階、空間六階精度的緊致差分格式．由于采用了向后差分，因此兩種格式均是無條件穩定的。

1 差分格式的建立

考慮如下二維非穩態對流擴散方程：

ut-α(uxx+uyy)+p(x，y，t)ux+q(x，y，t)uy=f(x，y，t) (x，y)∈Ω，t≥0

(1)

初始條件：

u(x，y，0)=g(x，y) (x，y)∈Ω

(2)

邊界條件：

u(x，y，t)=s(x，y，t) (x，y)∈?Ω，t>0

(3)

其中：Ω∈[a1，a2]×[b1，b2]為R2上的矩形區域，?Ω為Ω的邊界，u(x，y，t)為待求未知量，p(x，y，t)，q(x，y，t)分別為x，y方向的對流項系數，α為擴散項系數(常數)，f(x，y，t)為源項，且p(x，y，t)，q(x，y，t)，f(x，y，t)，g(x，y)，s(x，y，t)均為已知函數。

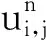
(4)

(5)

1.1 四階精度緊致格式

將方程(1)改寫為

ut=f(x，y，t)+α(uxx+uyy)-p(x，y，t)ux-q(x，y，t)uy

(6)

對二階導數uxx和uyy采用如下逼近：

(7)

(8)

將(7)，(8)式代入(6)式，考慮其在點(xi，yj)的值，得到

(9)

為了使(9)式空間保持四階精度，對ux和uy的計算采用如下四階Padé公式[9]

(10)

(11)

考慮(9)式在第n+1時間層的離散值，對ut采用如下二階BDF[10-11]進行離散

(12)

舍去高階項，可得

(13)

(14)

其中G為(9)式的右端項。

在文獻[12]中已經證明當K≤6(K代表精度)時，BDF是無條件穩定的．另外，由式(13)可以看出，在每個時間步上，該格式為5點模板的全隱格式．為了得到u(x，y，t)的計算值，(14)式中出現的ux和uy除需知道其內點值，還需知道其在邊界點處的值，為保持與內點差分格式同樣的精度，對邊界上的ux，uy采用一致四階邊界條件[2]計算。

1.2 六階精度緊致格式

為了得到方程(1)的六階精度的格式，需由Taylor級數展開得到一、二階導數的六階近似公式

(15)

(16)

(17)

(18)

將(15)-(18)式代入(6)式，有

(19)

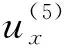
(20)

(21)

(22)

(23)

(24)

(25)

將(20)-(25)式代入(19)式，考慮其在點(xi，yj)的值，即可得到如下半離散的緊致格式

(26)

為了使(26)式具有六階精度，對ux和uy采用文獻[9]中的六階差分公式計算，uxx和uyy采用文獻[13]中的六階差分公式計算

(27)

(28)

(29)

(30)

考慮(26)式在第n+1時間層的值，對ut采用三階BDF[10]進行離散

(31)

略去高階項，可得

(32)

2 數值實驗

本文將利用以下4個問題進行數值實驗，驗證(2，4)格式和(3，6)格式的穩定性和有效性，文中涉及到的誤差及收斂階定義如下：

1) 最大絕對誤差：

2)L2范數誤差：

3) 收斂階：

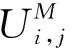
問題1考慮如下非齊次對流擴散問題

其精確解為u(x，t)=e-txy(1-x)(1-y)，初邊值條件及右端項f(x，y，t)均由精確解給出。

表1給出了問題1當τ=h2，t=0.5時的計算結果．從表中可以看出，本文(2，4)格式和文獻[6]格式在空間上均達到了四階精度，但本文(2，4)格式的計算結果比BTCS格式和文獻[6]格式更好； 本文(3，6)格式在空間上達到了六階精度(網格為64時的數值已經達到機器精度，所以收斂階受到影響不準確)，且最大絕對誤差比(2，4)格式的小2～3個數量級，計算結果更精確．當h=0.01，t=0.5時，不同時間步長τ下的L∞誤差、收斂階及CPU時間由表2給出．從表中可以看出，本文(2，4)格式時間上達到的精度為二階，本文(3，6)格式時間上達到的精度為三階，這與理論分析一致； 另外當τ較大時計算收斂慢，所用的CPU時間相對較長，計算過程中(3，6)格式需要計算在節點處的一、二階導數值，因此所用的計算時間比(2，4)格式長。

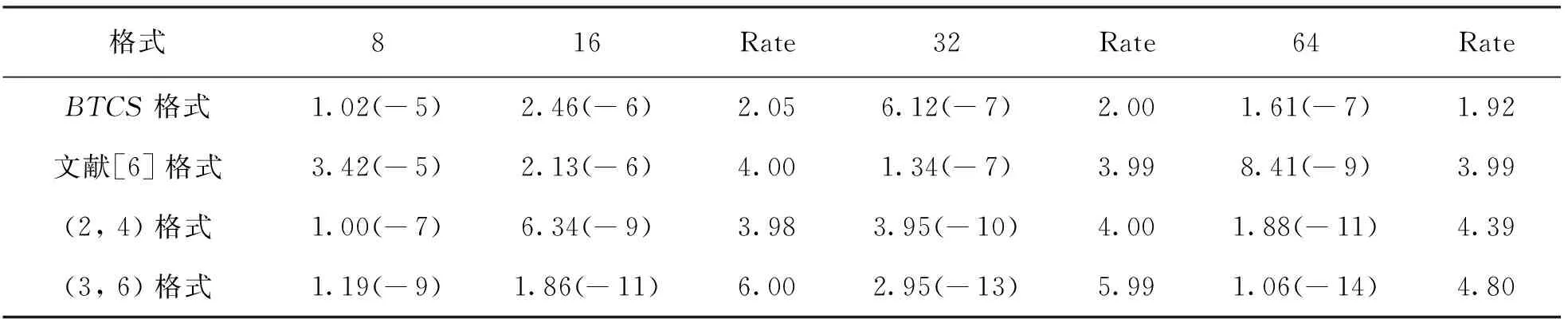
表1 問題1當τ=h2，t=0.5時的最大絕對誤差L∞及收斂階

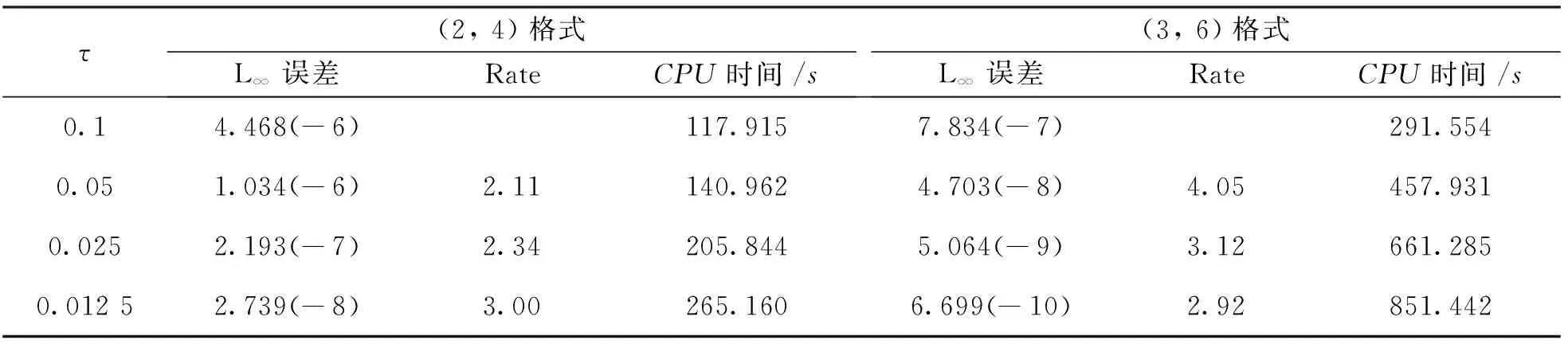
表2 問題1當h=0.01，t=0.5時的最大絕對誤差L∞，收斂階及CPU時間

問題2考慮如下變系數對流擴散問題

其精確解為u(x，t)=txy(1-x)(1-y)ex+y，初邊值條件及右端項f(x，y，t)均由精確解給出。

表3給出了問題2當τ=h2，t=0.25時本文格式與C-N格式和BTCS格式的L∞誤差及收斂階的比較．從表中可以看出，C-N格式和BTCS格式在空間上達到的精度均為二階，本文(2，4)格式在空間上達到的精度為四階，而本文(3，6)格式空間上達到的精度為六階，且(3，6)格式的計算結果誤差更小，充分驗證了本文兩種格式的精確性和有效性．另外，上述兩個例子的計算結果進一步說明低精度的啟動步并不影響格式的整體精度。

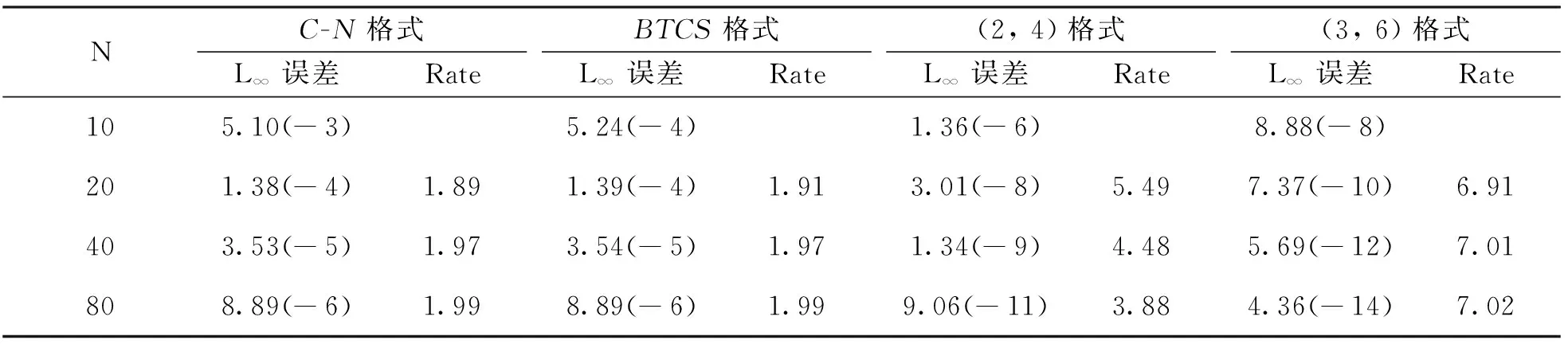
表3 問題2當τ=h2，t=0.25時的L∞誤差及收斂階

問題3考慮如下高斯脈沖問題

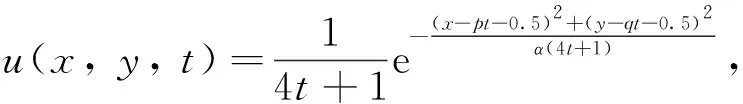
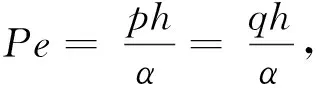
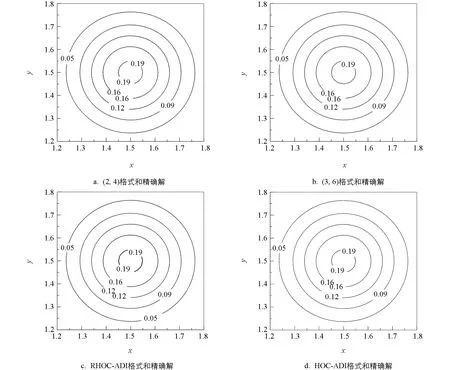
圖1 t=1，τ=2.5×10-3，Pe=2，1.2≤x，y≤1.8時的等值線圖

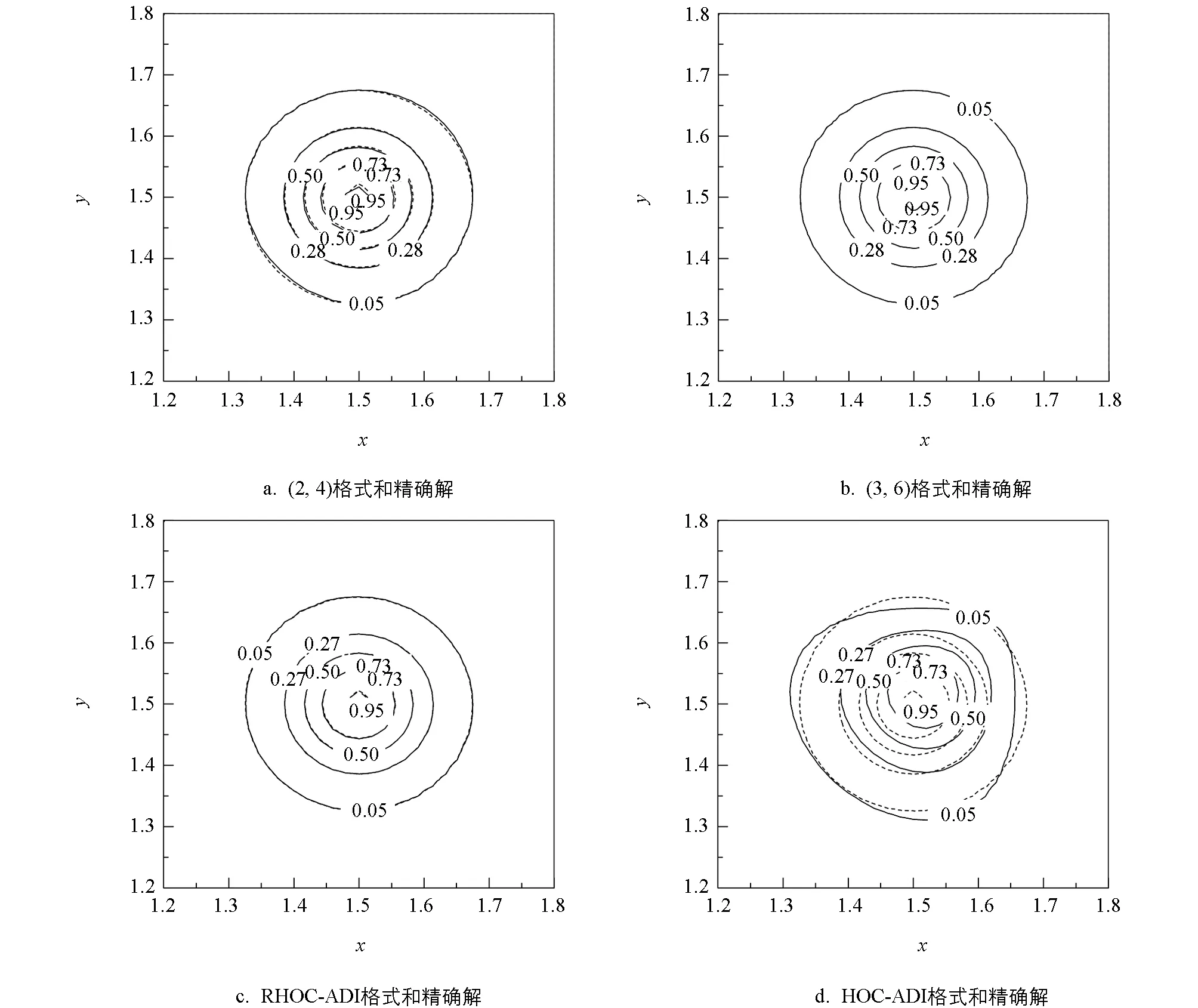
圖2 t=0.001，τ=2.5×10-6，Pe=2000，1.2≤x，y≤1.8時的等值線圖

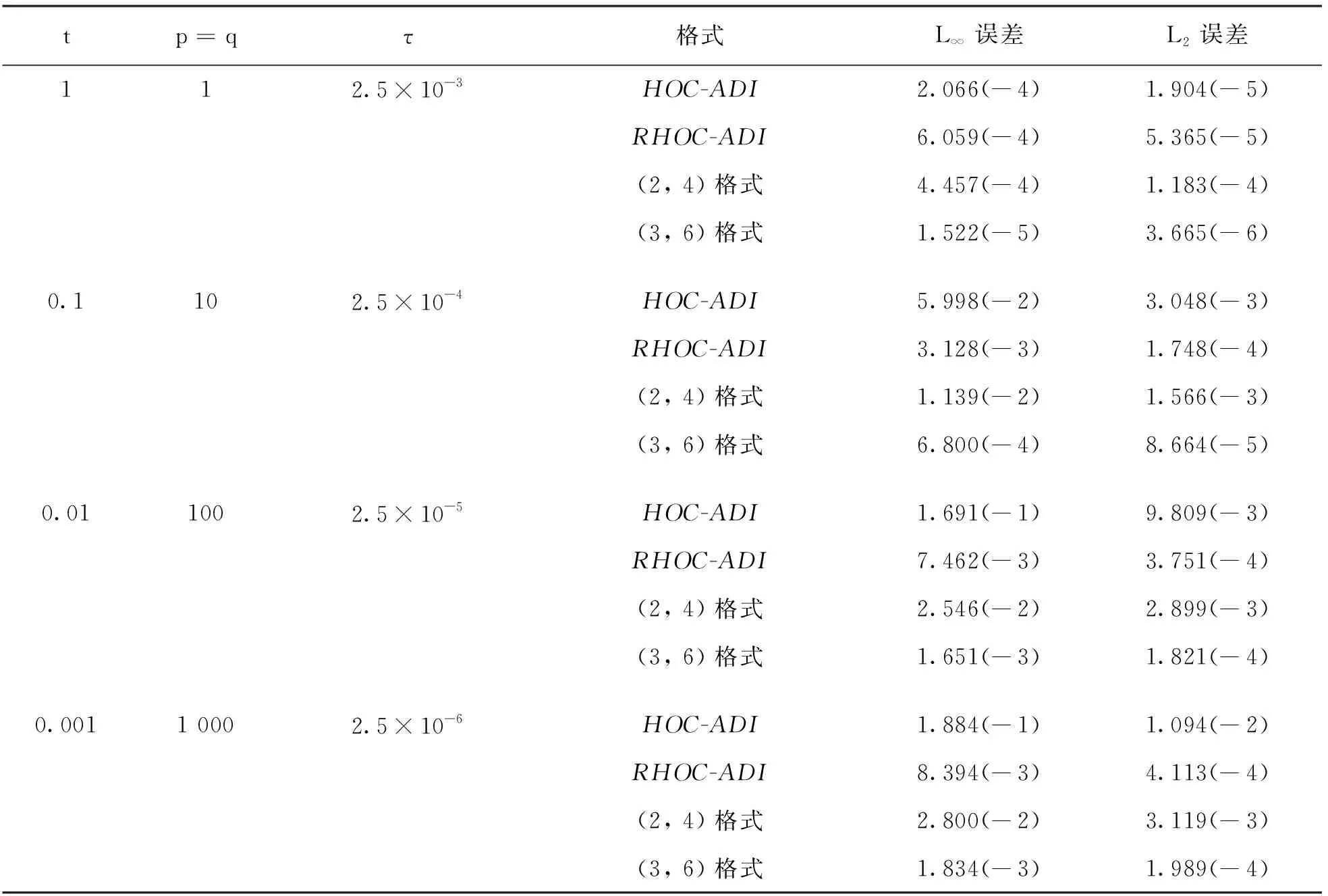
表4 問題3當h=0.02時在不同參數下的L∞誤差和L2誤差

問題4考慮如下非線性方程

表5給出了問題4當t=1，τ=h2時，本文(2，4)格式和(3，6)格式在α分別取1和0.1時的最大絕對誤差與收斂階．從表中可以看出，本文(2，4)格式在空間上達到的精度是四階，(3，6)格式達到的精度是六階(網格為64，α=1時最大絕對誤差的值已經達到機器精度)，這與理論推導是一致的，從表中還可以看出，α=1時所用的CPU時間比α=0.1時的長，(3，6)格式的CPU時間比(2，4)格式的長．表6給出了當N=7，τ=0.01，α=1時，t=15和t=20的計算解與精確解的絕對誤差．表中數據表明，本文(2，4)格式的計算誤差比文獻[14]格式小5～6個數量級，與文獻[15]格式的計算結果大致相當； 本文(3，6)格式的計算結果比文獻[14]格式小7～9個數量級，比文獻[15]格式小2～3個數量級．因此，對于此類非齊次邊界的Burgers方程，本文兩種高精度緊致差分格式非常有效．圖3給出了N=20，t=1，τ=0.01，α=0.1時本文兩種格式的絕對誤差和文獻[15]格式的絕對誤差比較，從圖中可以看出，本文(2，4)格式的絕對誤差與文獻[15]格式的絕對誤差大致相當，但本文(3，6)格式的計算結果更加精確，絕對誤差更小。

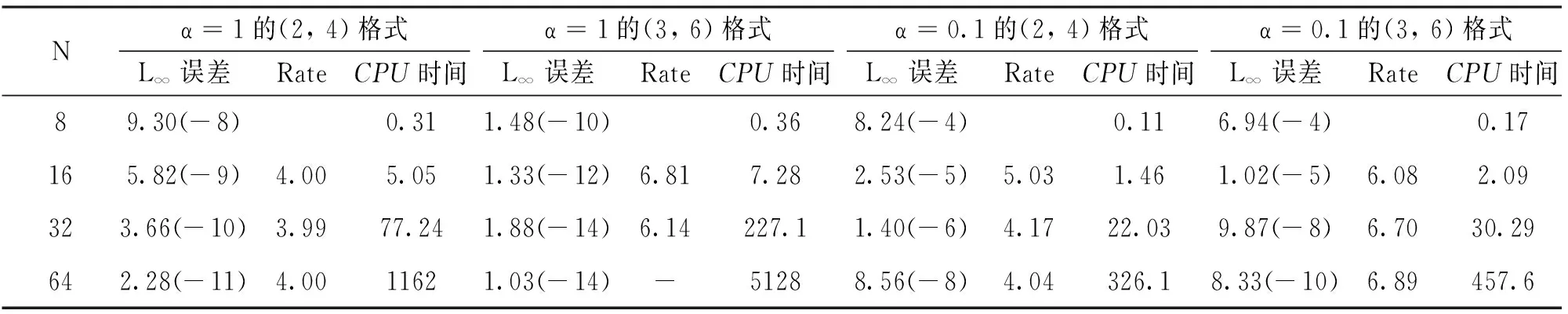
表5 問題 4 當τ=h2，t=1時的最大絕對誤差L∞，收斂階和CPU時間

表6 問題4當N=7，τ=0.01，α=1時的絕對誤差

續表6

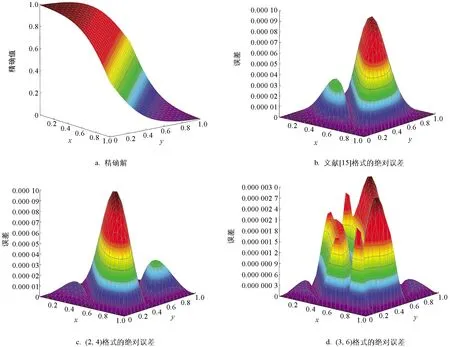
圖3 N=20，t=1，τ=0.01，α=0.1時的精確解與絕對誤差

3 結論