基于小撓度彎曲變形的鋁合金模板振動除渣分析

韓停偉，汪世益，2，李燦華，2,王 恒

(1.安徽工業大學，安徽 馬鞍山 243002；2.宣城市安工大工業技術研究院，安徽 宣城 242000)

0 引言

鋁合金混凝土模板目前被廣泛應用于建筑施工行業中，它具有質量較小、硬度大、使用方便、造價低且可以高效反復使用的優點。反復使用的鋁合金混凝土模板表面往往會粘附凝固的砂漿，因此，模板再次投入使用之前需要清理其表面的殘留砂漿，以保證混凝土墻壁表面的質量[1]。

本文對鋁合金模板及附著其上混凝土層的粘結進行分析,采用彈性力學小撓度彎曲理論[2]對四邊簡支的鋁合金模板進行振動模態分析和諧振響應分析，分析在外激勵振動作用下的鋁合金模板及附著的均質混凝土薄層之間的粘結應力關系和振動幅值比，考察鋁合金模板的振動除渣效果[3]。

1 模板及粘附混凝土層的粘結分析

某規格的鋁合金混凝土墻面模板如圖1所示，其長×寬×厚為2 800 mm×600 mm×4 mm，邊框高65 mm、寬20 mm；板面厚度4 mm遠小于中面的最小尺寸600 mm，且具有一定剛度，符合彈性力學薄板小撓度彎曲理論；設鋁合金模板上附著一層均質干混凝土薄層，也符合該理論。

圖1 鋁合金混凝土墻面模板示意圖

粘結在鋁合金模板上的干混凝土層和模板之間存在化學吸附力、摩阻力等，統稱粘結力。一般認為表面較為光滑的鋁合金面板和混凝土層之間的粘結力主要來自于化學吸附力，它和混凝土粘結劑有關。近年來，一些學者對相關問題進行了研究：邢國華等[4]對鋁合金板和混凝土的粘結進行研究；楊力軍等[5]采用湖南固特邦公司生產的JN建筑結構膠作為混凝土粘結劑，得到鋁合金板和其上粘附的均質混凝土層的粘結強度τu和極限荷載Fau的關系如式(1)所示：

(1)

設鋁合金模板上附著一層3 mm厚的均質混凝土薄層，由式(1)得，在該粘結劑作用下模板和均質混凝土層間的粘結強度計算值τu=1.182 MPa。對粘結面進行分析可知模板與混凝土連接面為薄弱面；素混凝土的抗拉強度很小，已知C30混凝土的最大抗拉強度為2.01 MPa，AL6061型鋁合金的抗拉強度為265 MPa，鋁合金材料的抗拉強度遠大于混凝土材料，且連接的粘結強度小于混凝土層的最大抗拉強度，于是它們粘結破壞的形態主要為界面的剪切破壞，當鋁合金模板彎曲產生的應力大于粘結強度時，那么混凝土層和鋁合金模板之間將發生相對滑移。

將鋁合金模板簡化為矩形薄板(如圖2所示)，以0點建立坐標系，長a、寬b、厚度h，在y=b/2、y=b/4處取6個點，均分a/2，標記為1～6點，在四邊簡支約束條件下矩形薄板中心位置點3處受集中載荷q=F0sinωt。

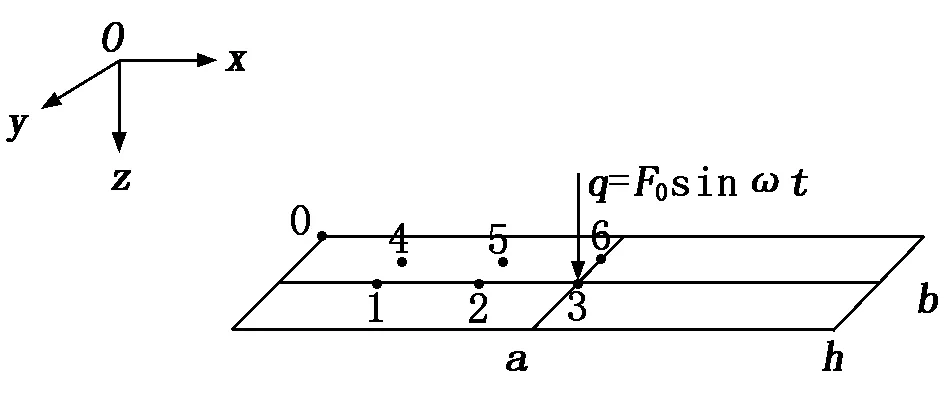
圖2 矩形薄板

鋁合金模板和附著其上的混凝土層之間的粘結剪應力τ和模板正應力σa的關系如式(2)[6]所示：

(2)

由彈性力學可知薄板受荷載q彎曲產生的正應力σa、撓度w如式(3)、式(4)所示：

(3)

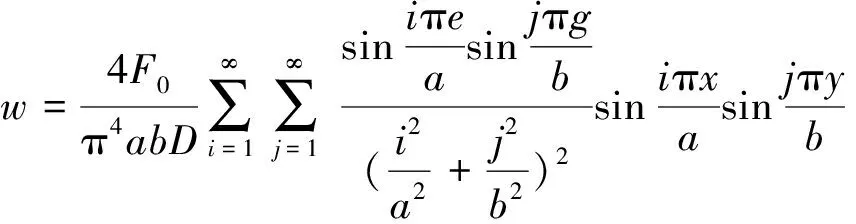
(4)

要使得混凝土和模板發生相對滑移，則正應力和混凝土粘結力強度的關系為：

(5)

在模板中心位置點3處施加集中荷載q，其幅值F0應該為混凝土薄層所受集中力和模板所受集中力之和，要破壞模板和附著其上混凝土薄層的粘結力，由式(3)、式(4)、式(5)計算可得：

F0>346.12 N.

當外激勵F0>346.12 N時，模板中心處表面和混凝土薄層發生粘結滑移，此時混凝土層四邊區域還和模板粘連，需要進行振動分離。

2 模板及粘附混凝土薄層的振動模態分析

2.1 基于小撓度彎曲理論的薄板振型函數

由彈性力學得圖2矩形薄板受迫橫向振動微分方程如式(6)所示：

(6)

薄板對應的自由振動的微分方程為：

(7)

設w(x,y,t)=W(x,y)sinωt，將其代入式(7)中得出振型微分方程：

(8)

其中：W為滿足相應邊界條件的振型函數。

四邊簡支的矩形薄板自由振動邊界條件為：

(9)

此時設薄板的振型為：

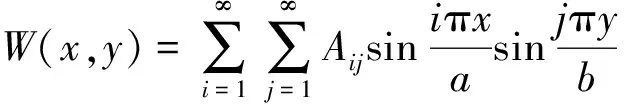
(10)

其中：Aij為待定系數。

令i和j取不同的整數值，可以求得相應的固有頻率為：

(11)

2.2 模板及粘附混凝土薄層的振動模態計算和有限元分析

AL6061型鋁合金材料和C30混凝土薄層的彈性模量E、密度ρ、泊松比μ、阻尼比ζ分別為7×104N/mm2、2 700 kg/m3、0.3、0.026和3×104N/mm2、2 300 kg/m3、0.18、0.05。應用MATLAB工具軟件[8]，根據式(10)、式(11)計算得到鋁合金墻面模板前4階模態的固有頻率分別為28.12 Hz、31.82 Hz、37.99 Hz、46.63 Hz；3 mm厚均質混凝土薄層的前4階模態固有頻率分別為14.51 Hz、16.42 Hz、19.61 Hz、24.07 Hz；鋁合金模板和混凝土薄層的振型一致，如圖3所示。

圖3 MATLAB計算得到的鋁合金模板和混凝土薄層的前4階振型

由于實際使用的鋁合金混凝土墻模板結構具有邊框和中間加強筋，因此根據式(10)、式(11)得到的計算結果與工程實際結果有偏差。對如圖1所示的模板及3 mm厚的均質混凝土薄層模型，應用ANSYS Workbench模態分析法[9,10]，在四邊簡支約束條件下，提取模板的前4階模態的固有頻率分別為45.95 Hz、61.73 Hz、71.39 Hz、80.45 Hz；3 mm厚均質混凝土薄層的前4階模態固有頻率分別為14.51 Hz、16.41 Hz、19.58 Hz、24.03 Hz。

ANSYS Workbench提取的3 mm厚混凝土層前4階模態如圖4所示，模板和混凝土薄層的前4階振動模態一致，固有頻率不同。

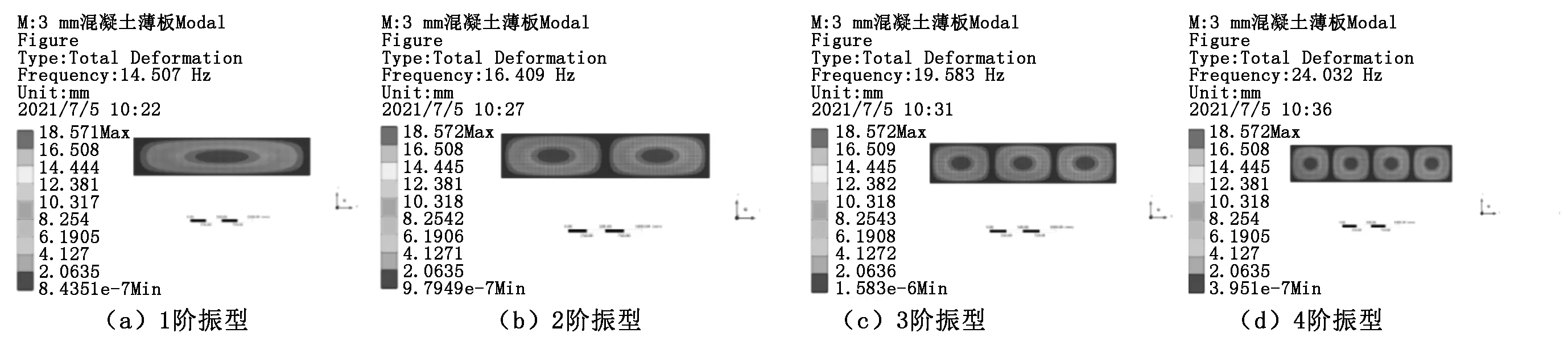
圖4 ANSYS Workbench提取的混凝土層前4階模態

圖3和圖4表明，根據薄板振動理論，由公式(9)和公式(10)計算得到的振型與用有限元分析的結果吻合，而固有頻率的理論計算值與有限元分析值存在差異，說明薄板小撓度振動彎曲理論適用于分析此類工程問題。

3 粘附于模板表面混凝土薄層的振動剝離分析

由振動力學知，當外激勵頻率f小于被激勵對象的基頻時，響應是一階的；當f大于基頻時響應是多階主振動的疊加[11]。設圖2中給定簡諧外激勵的作用點保持不變，從平衡位置開始，初始簡諧力初始位移、速度均為0，由式(6)和式(9)得振動響應撓度w表達式如式(12)所示：

(12)

模板和其均質混凝土薄層都存在阻尼，在簡諧振動過程中兩者輸出的振動響應幅值不同，設模板的振動響應幅值為w1，均質混凝土薄層振動響應幅值為w2，兩者的振動幅值比B為：

(13)

當外激勵頻率f=14.51 Hz和28.12 Hz時，圖2所示6個位置點的振動幅值比如表1所示。

表1 模板和3 mm混凝土薄層的振動響應幅值比

表1中，當外激勵頻率f=14.51 Hz時，附著在模板上的3 mm厚混凝土薄層共振，達到其一階模態，此時鋁合金模板振動響應幅值較小，各點的理論振幅比為0.07，ANSYS分析的幅值比為0.01，這是由于模板邊框和加強筋的存在使得ANSYS Workbench計算的固有頻率偏大，振幅偏小，軟件計算結果小于理論計算結果。

當外激勵頻率為鋁合金模板的理論一階固有頻率f=28.12 Hz時，各位置點的理論幅值比范圍為0～17.83，其中點1和點4的理論幅值比最大，點3和點6為節點；ANSYS分析的各位置點的幅值比范圍為0～0.45。表1的數據表明，模板和3 mm厚均質混凝土薄層的振動幅值比不同，振動位移響應不同，隨著時間的持續在簡諧振動狀態下薄層能從模板上分離。

4 結論

(1) 理論分析和ANSYS Workbench仿真分析結果表明，采用機械振動的方法能夠讓粘附于模板表面的均質混凝土薄層從模板表面剝離。

(2) 本文以某型號模板表面粘附厚度3 mm的均質混凝土層為例，諧振分析結果表明當外激勵大于346 N，振動頻率在14.51 Hz～28.12 Hz范圍時，振動除渣的效果較好。