一類實矩陣的符號穩定分析

劉 亮,龍 飛,楊 靖

(1.貴州大學電氣工程學院，貴州 貴陽 550025；2.貴州理工學院人工智能與電氣工程學院，貴州 貴陽 550003)

0 引言

符號穩定的概念來源于生態系統。生態領域的生物數量繁多且物種龐雜，受大自然等各種因素干擾卻一直維持著生態平衡，呈現出巨大的穩定性與魯棒性。研究人員把矩陣的符號與生態系統聯系到一起，通過分析不同生態物種間的動態變化過程來研究符號穩定[1-2]，從而得出了符號穩定的概念，并且取得了一定的研究成果[3-4]。

不少研究者已經得出了符號穩定的必要條件，并將其與生態系統中的關系一一對應[5]。Jeffries等從矩陣主對角線元素符號出發，提出了一種涂色測試法[6]來判斷矩陣的符號穩定，但該方法只對不可約矩陣有效。有相關學者從非對角線元素符號出發，分析一般矩陣符號穩定的充分條件[7]。由于符號穩定與矩陣元素大小無關，具有一種天然的魯棒穩定性，所以許多研究人員把符號穩定運用到不確定動態系統中。例如，將符號穩定運用到凸多面體不確定系統中，利用符號穩定配置系統矩陣的元素符號，實現不確定系統的魯棒鎮定[8-10]。

上述研究成果充分體現了符號穩定的優越性。本文利用赫爾維茨穩定判據分析矩陣符號型，得到了相應符號穩定的充分條件。最后對符號穩定進行了拓展，以便更好地運用到一些混雜系統中。

1 符號穩定的概念

1.1 符號穩定的定義

實矩陣可以用一個有向圖簡單、直觀地描述符號矩陣。

圖1 實矩陣A的有向圖

定義1[8]：如果與實矩陣A=(aij)n×n有相同符號型的任意實矩陣B都是赫爾維茨穩定的，則稱實矩陣A是符號穩定的，實矩陣A的符號矩陣sgnA也是符號穩定的。

1.2 符號穩定的必要條件

定理1[8]：實矩陣A=(aij)n×n符號穩定的必要條件如下。

(1)?i,aii≤0。

(2)至少存在一個i，使得aii<0。

(3)?i≠j,aijaji≤0。

(4)對于階數為三或三以上的實矩陣，都有aij·ajk· … ·aqr·ari=0。其中,i,j,k,…,q,r為元素的任意下標序列。

(5)detA≠0。

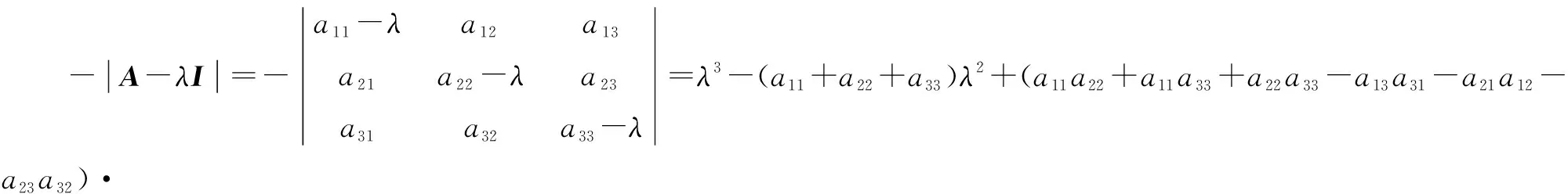
(1)

根據赫爾維茨穩定判據[11](線性系統穩定的必要條件是特征方程各項系數為正)，可知實矩陣A=(aij)n×n赫爾維茨穩定的必要條件為a11+a22+a33<0，(a11a22+a11a33+a22a33-a13a31-a21a12-a23a32)>0、(-a11a22a33-a13a32a21-a12a23a31+a13a31a22+a21a12a33+a23a32a11)>0。

若實矩陣A=(aij)n×n為符號穩定矩陣，可知符號穩定必要條件⑤必然滿足。

由a11+a22+a33<0可得aii≤0，且至少有1個為負，即符號穩定必要條件(1)和必要條件(2)。

由必要條件(1)和必要條件(2)可知a11a22+a11a33+a22a33≤0，而(a11a22+a11a33+a22a33-a13a31-a21a12-a23a32)>0，所以a13a31+a21a12+a23a32≤0，則aijaji≤0，即符號穩定必要條件(3)。

由必要條件(1)、必要條件(2)、必要條件(3)和必要條件(5)可知,(-a11a22a33+a13a31a22+a21a12a33+a23a32a11)>0，而(-a11a22a33-a13a32a21-a12a23a31+a13a31a22+a21a12a33+a23a32a11)>0，所以a13a32a21+a12a23a31≤0，即a13a32a21≤0且a12a23a31≤0。當a12a23a31<0時，有以下2種情況。

①3個元素全為負:假設a12<0、a23<0、a31<0，由必要條件(3)可知這3個元素分別關于主對角線對稱的元素a21≥0、a32≥0、a13≥0。當3個元素全部為正時，則a13a32a21>0，而a13a32a21+a12a23a31符號不確定，a13a32a21+a12a23a31≤0不一定成立。

②3個元素2正1負：假設a12>0、a23>0、a31<0，由必要條件(3)可知這3個元素分別關于主對角線對稱的元素a21≤0、a32≤0、a13≥0，則a13a32a21≥0。當a13a32a21>0時，a13a32a21+a12a23a31的符號不確定，a13a32a21+a12a23a31≤0不一定成立。

綜上所述，得a13a32a21=0，同理可證a12a23a31=0，即必要條件(4)。

1.3 符號穩定的充分條件

定理2：如果符號矩陣sgn[A=(aij)n×n]滿足以下3個條件，那么sgn[A=(aij)n×n]是符號穩定的。

①?i,aii<0。

②?i≠j,aijaji=0。

③對于階數為3以及3以上的實矩陣，都有aij·ajk· … ·aqr·ari=0。其中,i,j,k,…,q,r為元素的任意下標序列。

-|A-λI|=λ3-(a11+a22+a33)λ2+(a11a22+a11a33+a22a33-a13a31-a21a12-a23a32)λ+(-a11a22a33-a13a32a21-a12a23a31+a13a31a22+a21a12a33+a23a32a11)=λ3-(a11+a22+a33)λ2+(a11a22+a11a33+a22a33)λ-a11a22a33=(λ-a11)(λ-a22)(λ-a33)

(2)

那么λi=aii<0(i=1,2,3)。

此結論可以擴展到任意階矩陣。此符號穩定充分條件太過于嚴格，適用范圍狹窄。下面將從必要條件出發，分析符號穩定充分條件的一般性結論。

2 符號穩定的定性分析

由定義1可知，對符號穩定進行定性分析，即分析符號矩陣的赫爾維茨穩定。因此，從赫爾維茨穩定判據入手，對符號穩定進行定性分析。

2.1 赫爾維茨穩定判據

以3階實矩陣A=(aij)3×3為例，由式(1)和赫爾維茨穩定判據可知，實矩陣A赫爾維茨穩定的充要條件是a11+a22+a33<0、(a11a22+a11a33+a22a33-a13a31-a21a12-a23a32)>0、(-a11a22a33-a13a32a21-a12a23a31+a13a31a22+a21a12a33+a23a32a11)>0，且需滿足：

-(a11+a22+a33)(a11a22+a11a33+a22a33-a13a31-a21a12-a23a32)-(-a11a22a33-a13a32a21-a12a23a31+a13a31a22+a21a12a33+a23a32a11)>0

(3)

定理3:當實矩陣A=(aij)3×3有符號矩陣sgn[A=(aij)3×3]時，實矩陣A=(aij)3×3符號穩定的充要條件如下。

①實矩陣A=(aij)3×3滿足定理1。

②-(a11+a22+a33)(a11a22+a11a33+a22a33-a13a31-a21a12-a23a32)-(-a11a22a33-a13a32a21-a12a23a31+a13a31a22+a21a12a33+a23a32a11)>0成立。

由定理1的必要條件(4)可知，式(3)可以簡寫為：

(4)

結合定理1和式(4)可知，對符號穩定進行定性分析，即分析矩陣主對角線元素aii的符號與關于主對角線對稱的元素aijaji的符號的關系，也就是對應定理1中的必要條件(2)和必要條件(3)。

2.2 不可約矩陣的符號穩定充分條件

針對主對角線的元素符號，Jeffries等給出了1種涂色測試法[5-6]，用來判斷矩陣的符號穩定。但此法局限于不可約矩陣。

定義2：如果矩陣A是不可約矩陣(不可分解)，對于所有的i≠j，在矩陣A的有向圖中，有且僅有一條路徑從i到j。

定義3：矩陣A=(aij)n×n是1個可約矩陣，如果將1,2,…,n分成2個不相交的非空集合{i1,i2,…,iμ}和 {j1,j2,…,jv}，且μ+v=n，就使得aiαjβ=0，α=1,2,...,n,β=1,2,...,v。

定理4：如果符號矩陣的主對角線元素全為負數且滿足符號穩定的必要條件，則此符號矩陣是符號穩定的。

對于三階符號矩陣，由定理1的必要條件(3)和aii<0可知，式(4)必然成立。此3階符號矩陣為符號穩定矩陣。對于n階符號矩陣，可依據此方法進行證明。

定理5：對于不可約的符號矩陣，如果滿足符號穩定的必要條件且涂色測試法失效，則此符號矩陣是符號穩定的。

涂色測試法主要針對符號矩陣主對角線元素。矩陣主對角線元素為負數時，定義為黑色節點，表示為aib,ib；矩陣主對角線元素為0時，定義為白色節點，表示為aiw,iw。當矩陣主對角線元素僅有黑色節點或僅有白色節點時，不必進行涂色測試。因為主對角線元素僅有黑色節點時，可用定理4進行判定; 僅有白色節點時，不滿足符號穩定的必要條件，不是符號穩定的。因此，涂色測試主要針對黑色節點與白色節點共存的情況。在進行涂色測試之前，已確定矩陣滿足符號穩定的必要條件。進行涂色測試法的具體操作步驟如下。

①如果1個符號矩陣涂色測試成功，則表示所有aiw,jwajw,iw形式的乘積中，至少有1個此形式的乘積結果為負數。如果僅有1個白色節點，無法構成形如aiw,jwajw,iw的乘積形式，則涂色測試失效。如果僅有2個白色節點，可以構成1個形如aiw,jwajw,iw的乘積形式且乘積結果為負數，則涂色測試成功。

②所有ajb,iwaiw,jb形式的乘積中，對于黑色節點jb，當ajb,iwaiw,jb的乘積結果為負數，且ajb,kwakw,jb的乘積結果也為負數(iw≠kw)時，則涂色測試成功。

以3階矩陣為例，對于1個不可約的3階符號矩陣sgn[A=(aij)3×3]，如果它是符號穩定的，則其滿足定理1且式(4)成立，即式(5)～式(10)成立。

a11+a22+a33<0

(5)

(a11a22+a11a33+a22a33-a13a31-a21a12-a23a32)>0

(6)

-a11a22a33+a13a31a22+a21a12a33+a23a32a11>0

(7)

a13a32a21=0

(8)

a12a23a31=0

(9)

(10)

其中，式(5)～式(9)式是符號矩陣sgn[A=(aij)3×3]符號穩定的必要條件，式(5)～式(10)是矩陣sgn[A=(aij)3×3]符號穩定的充要條件。在使用涂色測試法之前，已知矩陣滿足式(5)～式(9)，所以涂色測試法是從定理1中的必要條件(2)入手，針對式 (10)而設計的。

2.3 一般矩陣符號穩定的充分條件

涂色測試法雖然提供了完整的、判斷符號穩定的充分條件，但方法復雜，使用繁瑣，且局限性大。因此，研究者提出了1種比較簡單的充分條件來驗證符號穩定。與涂色測試法不同的是，此方法是從定理1的必要條件(3)入手，針對式(10)而設計的。

分析一般矩陣符號穩定充分條件的預備知識點[7]如下。

①關于主對角線對稱的2個元素的乘積算式稱為相互作用對，即aijaji(i≠j)。如果aijaji<0，則稱aijaji為OS對。如果aijaji=0，則稱aijaji為ZS對。在aijaji=0中，如果2個元素符號分別為正和零，則稱aijaji為ZSp對。如果2個元素符號分別為負和零，則稱aijaji為ZSn對。如果2個元素符號都為零，則稱aijaji為ZZ對。

②滿足定理1條件的矩陣定義為ISS矩陣；滿足符號穩定充分條件的矩陣定義為QLSS矩陣。

③矩陣的主對角線上，關于中點對稱的2個元素相加的形式定義為MIDMT,如4階矩陣中的a11+a44和a22+a33。主對角線任意2個元素的相加定義為MT，如4階矩陣中的a11+a22、a33+a44和a11+a33等。

n階ISS矩陣最多有(n-1)個OS對，當超過(n-1)個OS對時，將不滿足定理1中的必要條件(4)。由定義2可知，n階不可約矩陣有且僅有(n-1)個OS對，其余全為ZZ對。

下面將從OS對的個數來分析符號穩定的充分條件。

定理6：1個n階ISS矩陣的OS對個數為0，則為QLSS矩陣。

證明：以3階矩陣為例，n階矩陣可按照此方法證明。

3階ISS矩陣sgn[A=(aij)3×3]必滿足式(5)～式(9)。3階QLSS矩陣sgn[A=(aij)3×3]必滿足式(5)～式(10)。如果3階ISS矩陣sgn[A=(aij)3×3]中OS對的個數是0，則由式(5)和式(7)可知a11<0、a22<0,a33<0，式(10)必然成立。

定理7：如果1個n階ISS矩陣的OS對個數小于(n-1)個，且滿足下列任意1個條件，則為QLSS矩陣。

①n階ISS矩陣中所有QS對使得相應的MT非零。

②n階ISS矩陣中所有ZSp對使得相應的MT非零。

定理8：如果1個n階ISS矩陣的OS對個數是(n-1)，且滿足下列任意1個條件，則為QLSS矩陣。

①反主對角線上至少存在1個OS對，使得相應的MIDMT非零。

②反主對角線上至少存在1個ZZ對，使得相應的MIDMT非零。

定理5和定理8描述的是同一種符號矩陣。不同的是，定理5中的涂色測試法是從主對角線元素的符號來分析符號穩定，定理8是從反主對角線相互作用對的符號來分析符號穩定。

定理9：一個可約的ISS矩陣A可以分解為q個Ai，即detA=detA1×detA2×…×detAq。當且僅當Ai(i=1,2,...,q)全為QLSS矩陣時，A是QLSS矩陣。

注1：對于1個n階ISS矩陣，如果OS對的個數小于(n-1)個，且可分解為多個矩陣。根據定理9可知，分析n階ISS矩陣的符號穩定性，等同于分析分解的多個矩陣的符號穩定性。

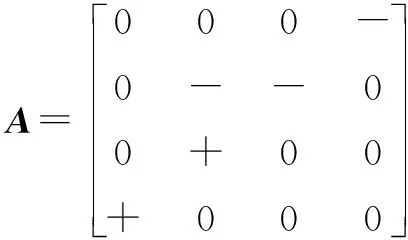
圖2 A和B的有向圖(I)

3 符號穩定的驗證示例

驗證：矩陣A是1個5階ISS矩陣，有4個OS對，是1個不可約矩陣。可用定理5和定理8進行判斷。運用定理5對其進行涂色測試，a11、a22、a44、a55是黑色節點，a33是白色節點。使用涂色測試法進行驗證，涂色測試成功，所以A不是1個QLSS矩陣。運用定理8，不滿足條件①和條件②，所以A不是一個QLSS矩陣。

驗證：矩陣A是1個5階ISS矩陣，有4個OS對，是1個不可約矩陣。可用定理5和定理8進行判斷。運用定理5對其進行涂色測試，a22、a33、a44、a55是黑色節點，a11是白色節點。使用涂色測試法進行驗證：涂色測試失效，所以A是1個QLSS矩陣。運用定理8，因為矩陣A滿足條件②，所以A是1個QLSS矩陣。

驗證：矩陣A是1個4階ISS矩陣，有2個OS對。可用定理7進行判斷：矩陣A不滿足條件①，而條件②不適用于矩陣A，所以A不是1個QLSS矩陣。通過有向圖可知，矩陣A可以分解為2個矩陣，用定理9進行判斷。因為其中1個分解矩陣不是QLSS矩陣，所以A不是1個QLSS矩陣。

驗證：矩陣A是1個4階ISS矩陣，有2個OS對和2個ZSn對。可用定理7進行判斷：矩陣A滿足條件①，而條件②不適用于矩陣A，所以A是1個QLSS矩陣。

4 符號穩定的相關結論

定理10：如果1個矩陣的有向圖結構與1個QLSS矩陣的有向圖結構相同，則這個矩陣也是QLSS矩陣。

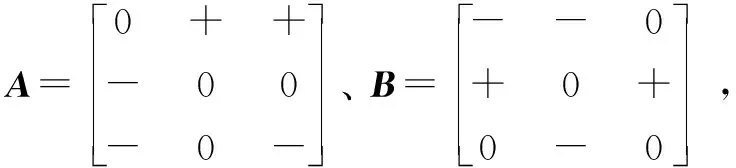
圖3 A和B的有向圖(II)

證明：假設A為QLSS矩陣;P為1個與A階數相同的置換矩陣，B=PTAP,因此A與B合同。由合同的性質可知，A和B有相同的正負慣性指數，即正負特征值個數相同。因為A是QLSS矩陣，所以B也是QLSS矩陣。此時，A和B的有向圖結構相同。

對A作初等變換，不會改變A的有向圖結構。一次初等行變換和一次對應的初等列變換對應著有向圖2個對應位置處的節點交換。

定義4：由具有相同有向圖結構的符號矩陣組成的1個符號矩陣集合，如果其中任意1個符號矩陣是符號穩定的，則稱這個集合為穩定集。如果矩陣的階數是n，其子集個數為n!，則稱這個集合為完整穩定集。

這個矩陣的有向圖結構相同的矩陣構成的1個完整穩定集為：

定理11[8]：對于所有符號穩定且主對角線元素均為負數的n階矩陣A=(aij)n×n，其所有特征值的實部有界且滿足以下要求。特征值實部絕對值的下界是所有對角線元素絕對值的最小值，特征值實部絕對值的上界是所有對角線元素絕對值的最大值，即：

|aii|min≤|Re(λi)|min≤|Re(λi)|max≤|aii|max

(11)

對于A=(aij)n×n部分主對角線元素為0的情況，有：

0<|Re(λi)|min≤|Re(λi)|max≤|aii|max

(12)

給定1個n階矩陣An×n和1個m階矩陣Bm×m，?表示Kronecker積[12]，⊕表示Kronecker和[12]。

(13)

引理12[12]：矩陣An×n的特征值是λi(i=1,2,…,n)，矩陣Bm×m的特征值是μj(j=1,2,…,m)，則An×n⊕Bm×m的特征值為λi+μj(i=1,2,…n;j=1,2,…,m)。

定理13：如果sgn[A=(aij)n×n]和sgn[B=(aij)m×m]都是符號穩定的，則sgn[A=(aij)n×n]?sgn[B=(aij)m×m]也是符號穩定的。

證明：假設sgn[A=(aij)n×n]的特征值是λi，sgn[B=(aij)m×m]的特征值是μj。因為sgn[A=(aij)n×n]和sgn[B=(aij)m×m] 都是符號穩定的，所以Re(λi)<0、Re(μj)<0，可得Re(λi+μj)<0。由引理12可知，sgn[A=(aij)n×n]?sgn[B=(aij)m×m]也是符號穩定的。

赫爾維茨穩定和Schur穩定是2種非常重要的穩定概念。符號穩定是1種打破傳統數值型的赫爾維茨穩定。下面將進一步分析符號矩陣與Schur穩定之間的聯系。

如果矩陣A=(aij)n×n滿足aijaji=0(i≠j)，且對于階數為3或3以上的矩陣都有aij·ajk· … ·aqr·ari=0(i,j,k,…,q,r為元素的任意下標序列)，那么矩陣A=(aij)n×n的特征值為主對角線元素。

定理14：當符號矩陣sgn[A=(aij)n×n]滿足以下條件時，矩陣A=(aij)n×n是Schur穩定的。

①|aii|<1。

②aijaji=0(i≠j)。

③對于階數為3或3以上的矩陣都有aij·ajk· … ·aqr·ari=0。其中i,j,k,…,q,r為元素的任意下標序列。

定理15：當符號矩陣sgn[A=(aij)n×n]滿足以下條件時，矩陣A=(aij)n×n是Schur穩定的。

①0≤aii<1。

②aijaji=0(i≠j)。

③對于階數為3或3以上的矩陣都有aij·ajk·…·aqr·ari=0。其中，i,j,k,…,q,r為元素的任意下標序列。

定理14和定理15分別對一般矩陣和正矩陣定義了1種符號型Schur穩定。在一般矩陣中，其相互作用對可以是ZSp對、ZSn對或 ZZ對。在正矩陣中，其相互作用對只能是ZSp對或ZZ對。

定理16：當符號矩陣sgn[A=(aij)n×n]滿足以下條件時，則矩陣A=(aij)n×n既是Schur穩定的，又是赫爾維茨穩定的。

①-1

②aijaji=0(i≠j)。

③對于階數為3或3以上的矩陣都有aij·ajk·…·aqr·ari=0。其中,i,j,k,…,q,r為元素的任意下標序列。

定理17：如果符號矩陣sgn[A=(aij)n×n]是正矩陣，則以下2個條件等價。

①sgn[A=(aij)n×n]是Schur穩定的。

②sgn[A=(aij)n×n]-In×n是赫爾維茨穩定的。

證明：條件①→條件②。由定理15可知，如果sgn[A=(aij)n×n]是Schur穩定的，則0≤aii<1。對于矩陣sgn[A=(aij)n×n]-In×n，其對角線元素aii-1<0。由定理16可知，sgn[A=(aij)n×n]-In×n是赫爾維茨穩定的。

條件②→條件①。由定理16可知，如果sgn[A=(aij)n×n]-In×n是赫爾維茨穩定，則aii-1<0，得aii<1。由正矩陣sgn[A=(aij)n×n]得aii>0，所以0≤aii<1。由定理15可知,sgn[A=(aij)n×n]是Schur穩定的。

5 結論

本文通過定義符號穩定，首先從符號穩定的必要條件出發，利用赫爾維茨穩定判據分析了符號穩定的充分條件。然后，用具體例子來驗證所得的充分條件，對符號穩定充分條件作出了一般性結論。最后，將符號穩定推廣到符號Schur穩定，使其在一些不確定系統(例如隨機系統、切換系統等)中的應用更加廣泛。