變壓器問題的解題策略

貴州 楊 勇

變壓器問題考查的是電磁感應知識的應用，處理此類問題通常用到的是原、副線圈的電壓比和匝數比的關系、電流比和匝數比的關系、功率相關知識。但是由于負載變化之后，電流、電壓都有可能發生變化，如果原線圈所在回路有電阻，會給分析帶來更大的困難。為能更好地分析和理解此類問題，本文將以湖南省2021年高考物理第6題為基礎，分析、拓展和總結變壓器問題的解決方法。

一、高考試題分析

如圖1所示，理想變壓器原、副線圈匝數比為n1∶n2，輸入端C、D接入電壓有效值恒定的交變電源，燈泡L1、L2的阻值始終與定值電阻R0的阻值相同。在滑動變阻器R的滑片從a端滑動到b端的過程中，兩個燈泡始終發光且工作在額定電壓以內，下列說法正確的是

( )

圖1

A.L1先變暗后變亮，L2一直變亮

B.L1先變亮后變暗，L2一直變亮

C.L1先變暗后變亮，L2先變亮后變暗

D.L1先變亮后變暗，L2先變亮后變暗

【試題分析】本題是一道常見的變壓器問題，但是對于學生來說有一定的困難。首先，由于原線圈連接有用電器，所以原線圈的電壓會發生變化，則副線圈的電壓也隨之變化，給分析帶來困難；其次，副線圈的電阻發生變化，影響著整個電路的相關參量，單獨討論某個電阻的參量時比較困難；最后，電阻R的變化要用到數學極值討論問題。如果能突破以上的三個問題，此題便迎刃而解。

【試題解析】由于電源的輸出電壓的有效值不變，則一系列的變化由負載引起，分析此電路時從負載出發，把L2、R0、R混聯之后的總電阻記為R負，根據電路的特點，當滑動變阻器的滑片在a、b之間某個位置時，滑片到a端之間的電阻為Ra，滑片到b端之間的電阻為Rb，根據電路結構可以得到

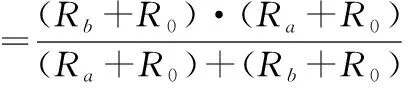
把電路等效為如圖2所示電路，電源輸出的電壓為U，原線圈的電壓為U1、電流為I1，副線圈的電壓為U2、電流為I2，則

U=U1+I1R0，U2=I2R負

圖3

【試題評價】本題考查學生對電路結構的理解、電路動態分析的能力和變壓器的電壓、電流、匝數之間的關系，同時結合實際分析燈泡的明暗程度與功率的關系，充分體現了應用數學知識處理物理問題能力的培養。從以上的常規解析來看，分析的過程是比較復雜的，如果考生不具備一定的獨立思考的能力，解題是比較困難的，下面將進一步討論有關變壓器的相關問題。

二、等效法分析變壓器問題

對于理想變壓器來說，由于變壓器在電路中只是改變電壓，所以在分析有理想變壓器問題時，可以把變壓器與負載看成一個整體，這樣會使電路結構變得簡單，處理問題變得容易。

如圖4所示，根據變壓器的輸入功率和輸出功率相等，且輸出功率等于負載消耗的總功率，把虛線部分等效成一個電阻R等，則可以等效為圖5所示電路

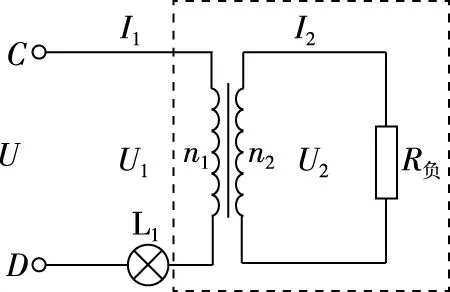
圖4

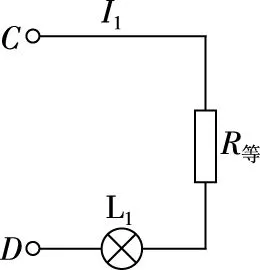
圖5

1.理想變壓器輸入端與電阻串聯的動態分析

【例1】(2021·湖南卷第6題改編)如圖6所示，理想變壓器原、副線圈匝數比為n1∶n2=2∶1，輸入端C、D接入電壓有效值恒定為8 V的交變電源，燈泡L1、L2的阻值始終與定值電阻R0=2 Ω的阻值相同。滑動變阻器的最大阻值為4 Ω，在滑動變阻器R的滑片從a端滑動到b端的過程中，兩個燈泡始終發光且在額定電壓以內工作，求變壓器輸出的最大功率？

圖6

【分析】由于原線圈上用電器串聯，滑動變阻器的阻值改變會影響變壓器的輸入電壓，同時也影響著副線圈的電壓，所以要用數學推導，把變壓器的傳輸功率的表達式寫出來，如果數學功底不好，可能會得到錯誤的答案。因此借助上述的分析，可以把變壓器與負載看成一個等效電阻，燈泡L1等效為電源的內阻，則當外電阻等于內電阻時，電源輸出的功率最大。

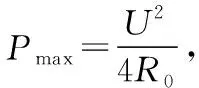
圖7

【評價】對于原線圈回路上有用電器的變壓器問題，如果用常規的方法寫出表達式，對于數學功底較弱的學生來說具有一定的困難，但是如果能夠掌握變壓器的等效方法，可以把復雜的電路簡化，使其變成我們熟悉的電路。本題解題的方法主要是掌握電源輸出功率與外電阻的變化關系，把復雜電路簡化成簡單的閉合電路。此方法除了分析變壓器的傳輸功率的最值問題外，還可以分析電路的電流、電壓變化情況。

2.理想變壓器輸入端與電阻并聯的動態分析

在例1的條件下，如果燈泡L1與原線圈并聯，如圖8所示，求變壓器傳輸的最大功率？

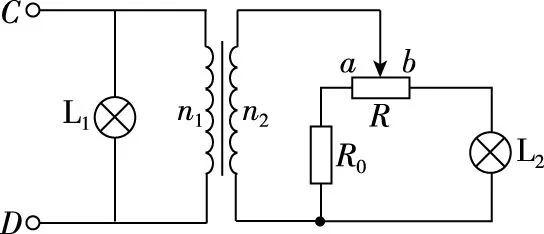
圖8

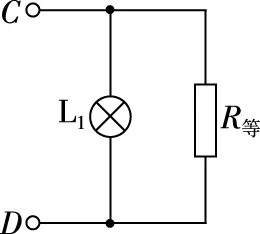
圖9

【評價】從上述的兩種情況來看，應用等效法處理理想變壓器的動態問題比常規方法要簡捷得多，應用好等效法不僅能快捷解題，還能使學生的思維得到發散。對于變壓器的等效處理，可以把電源部分與變壓器等效為一個整體，讀者可以通過上述的等效思路進行分析，應用變壓器與電源等效分析，看是否得到相同的結果。

三、變壓器問題的拓展分析

1.非理想變壓器的問題分析

( )

A.7 A B.5 A C.3 A D.2 A

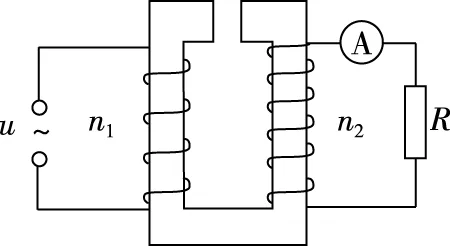
圖10

【分析】本題是非理想變壓器，由于鐵芯中間斷開，則會有漏磁現象，因此原、副線圈的磁通量變化率不相等，但是根據題述，解決此題還是從理想變壓器出發，再結合實際情況選出符合的答案。

【評價】對于此類問題，很多學生容易選擇C選項，因為在學生的大腦中已經形成一種定勢，習慣于電壓比等于匝數之比，沒有結合實際和題述的表達，導致選出錯誤的答案，那么在備考復習中，一定要充分認識和理解變壓器的原理及理想變壓器的意義，在遇到相應問題時才能清楚地找到正確的答案，因此，在教學中要培養學生敏銳的思維和積極思考問題的能力。

2.理想變壓器磁路并聯問題的分析

【例3】如圖是某變壓器等臂鐵芯的示意圖，已知線圈1、2的匝數之比n1∶n2=2∶1。在不接負載的情況下

( )

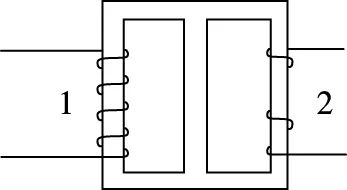
圖11

A.當線圈1輸入電壓為220 V時，線圈2輸出電壓為110 V

B.當線圈1輸入電壓為220 V時，線圈2輸出電壓為55 V

C.當線圈2輸入電壓為110 V時，線圈1輸出電壓為220 V

D.當線圈2輸入電壓為110 V時，線圈1輸出電壓為440 V

【分析】本題涉及的也是普通變壓器模型，因為有多個“磁路”，很多學生拿到此題直接應用教材上的電壓比與匝數比的關系，直接得到A答案，但是要處理好本題得了解“磁路”的特征。

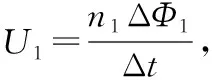
圖12

【拓展變式】如圖13，線圈1、2的匝數之比n1∶n2=2∶1，當線圈1輸入的電壓為220 V時，線圈2的電壓是多少？

圖13

【評價】對于多“磁路”的變壓器問題，雖然在高中階段很少遇到，但是對于變壓器原理一定要充分理解，不能死記教材上的公式，要真正理解電壓比與匝數比的含義，這樣在遇到稍微復雜的問題時，才能應用自如，把握物理規律，掌握內涵，培養對問題獨立思考的能力，提升物理核心素養。

【總結】以上是從高考試題出發，分析高考試題出現的解題困難，總結處理變壓器動態分析的方法，拓展分析高中階段可能出現的問題，對于以上描述的變壓器問題，大致的處理思路如下：

1.如果是單“磁路”理想變壓器，可以直接應用教材的公式，電壓比等于匝數比；

2.如果原線圈上沒有用電器，則可以直接分析負載的變化情況，根據電路原理分析相關參量的變化情況；

3.如果原線圈上接有用電器，在分析電路的動態變化時，應用等效方法較為簡單；

4.如果有“多磁路”的變壓器或者非理想變壓器，一定從實際出發，不能直接套用公式，以免錯誤。