基于曲軸輪廓誤差分析的隨動磨床軸性能預測*

房小艷 盛曉偉 孫以澤

(①東華大學機械工程學院，上海 201620；②上海機床廠有限公司上海磨床研究所，上海 200093)

曲軸是汽車發動機的關鍵部件，其加工質量直接影響發動機的性能和可靠性，因此曲軸加工在汽車工業中起著重要的作用。在大規模汽車發動機曲軸生產線上，為了滿足加工精度和效率要求，數控曲軸隨動磨床已被廣泛使用[1-2]。曲軸隨動磨削是通過控制工件的回轉軸(C軸)和砂輪的橫向進給軸(X軸)即C-X兩軸聯動的方式保持砂輪外圓和曲軸連桿頸始終相切[3-6]。隨動磨削方法比需要適當夾具和反復調整回轉中心的傳統磨削方法具有更高的加工效率，更高的柔性和更高的精度[1]。依據隨動磨削工藝的特點，曲軸輪廓誤差中包括隨動磨床C軸和X軸的位置控制誤差信息，而曲軸輪廓誤差又是曲軸生產現場隨機抽檢最直觀的數據。因此，如果能夠找出曲軸輪廓誤差和隨動磨床C軸、X軸位置控制誤差之間的對應關系，就能夠通過曲軸輪廓誤差分析去預測隨動磨床C軸和X軸的性能，對于曲軸隨動磨床的可靠性維護具有重要意義。

曲軸輪廓誤差中蘊含著隨動磨床的性能信息，砂輪的狀態信息和曲軸材料的特征信息[7]。傳統的輪廓誤差信號分析方法大多以積分變換為基礎，如傅里葉變換、小波變換等，需要根據輪廓誤差信號特征人工設計選擇合適的基函數，匹配信號特征分量。積分變換方法對人工先驗知識依賴性較強，在分析處理實際的復雜多變信號時缺少自由度和自適應性，難以同時兼顧并有效提取信號中的各種變化特征。自從Huang N E等提出經驗模態分解(empirical mode decomposition, EMD)方法[8]和集總經驗模態分解(ensemble empirical mode decomposition, EEMD)方法[9]以來，吸引了眾多學者的關注。近年來出現了多種新的信號分解方法，比如局部均值分解(local mean decomposition, LMD)方法[10]、本質時間尺度分解(intrinsic time-scale decomposition, ITD)方法[11]、經驗小波變換(empirical wavelet transform, EWT)方法[12]、變分模態分解(variational mode decomposition, VMD)方法[13]和自適應局部迭代濾波(adaptive local iterative filtering, ALIT)方法[14]等。以上信號分解方法無需根據先驗知識設計基函數，分解是后驗的，完全由數據驅動，對信號變化具有自適應能力，因此該類分解方法統稱為自適應模態分解方法。各種自適應模態分解方法各有優劣，適用于不同類型的復雜信號分解。本文作者在文獻[7]中提出基于EEMD的曲軸輪廓誤差分析方法，雖然該方法可以分解出與隨動磨床C軸和X軸相對應的分量，但是無論在方便性、快速性還是分解質量上都與本文提出的方法有所差距。

本文首先給出由隨動磨床軸位置控制誤差計算曲軸輪廓誤差的方法。其次提出基于VMD的曲軸輪廓誤差分析方法。最后采用提出的計算和分析方法，找出曲軸輪廓誤差與隨動磨床C軸和X軸位置控制誤差之間的對應關系，從而實現由曲軸輪廓誤差分析對隨動磨床軸性能的預測。

1 由軸位置控制誤差計算曲軸輪廓誤差的方法

曲軸隨動磨床結構簡圖及所研究誤差數據來源如圖1所示，曲軸磨削后可測量曲軸各連桿頸的輪廓誤差。曲軸隨動磨床的數控系統具有跟蹤功能，可實時采集C軸和X軸的位置控制誤差。

在隨動磨削過程中，砂輪總是與曲軸連桿頸相切，曲軸連桿頸的輪廓是由砂輪的往復運動跟隨曲軸的回轉運動形成的[7]。在理想情況下，曲軸連桿頸的輪廓是一個標準的圓，此時隨動磨床的C軸和X軸滿足磨削運動理論控制方程。然而，在實際加工中，C軸和X軸的運動控制均有誤差，因此，實際磨削得到的曲軸連桿頸并不是一個標準的圓。對實際加工得到的曲軸連桿頸輪廓采用最小二乘擬合可以獲得基圓，實際輪廓和基圓的差就是輪廓誤差[7]。在位置控制中，實際值和理論值的偏差是不可避免的，因此，導致曲軸連桿頸輪廓誤差的主要根源就是C軸和X軸的位置控制誤差。由C軸和X軸位置控制誤差計算曲軸輪廓誤差的過程如圖2所示。

2 基于VMD的曲軸輪廓誤差分析方法

VMD方法是一種非遞歸分解方法，它能夠自適應得將復雜多分量信號分解為調幅-調頻分量，而且對噪聲穩定[13]。VMD將分解后的本證模態函數(intrinsic mode functions, IMFs)定義為解析的調幅-調頻模型，將調幅-調頻模型參數與IMF帶寬關聯。根據IMF的窄帶性質，通過帶寬最小化求解調幅-調頻參數，從而獲得IMF。同其他自適應模態分解方法相比，VMD具有嚴密的數學理論基礎支持[15]。當使用VMD方法分解信號時，約束變分優化問題為：

(2)

式中：uk(t) 為第k個IMF；ωk為對應的中心頻率；K為分解的數目；x(t)為待分解信號。

為了將式(2)的約束變分優化問題轉化為無約束問題，需要引入二次懲罰因子α和Lagrange乘子λ，以便快速收斂并增強約束。通過引進這兩個參數，增廣的Lagrange表達式如下所示：

L[{uk(t)},{ωk},λ(t)]

式中：〈,〉表示內積。

VMD的完整算法如下：

(4)

(5)

λn+1=λn+

(6)

(3) 檢查收斂條件：

(7)

式中：ε為收斂終止條件，如果滿足條件，則停止分解，否則令n=n+1，返回步驟(2)。

3 磨削實驗及誤差數據分析結果

3.1 磨削實驗

一臺數控隨動磨床用來加工曲軸連桿頸，該機床型號是上海機床廠有限公司研制的H405-BF數控曲軸隨動磨床，磨削實驗布局如圖3所示。數控系統是西門子840D，在曲軸磨削過程中，使用具有跟蹤功能的數控系統實時采集C軸和X軸的位置控制誤差。磨削完成后，測量曲軸連桿頸的輪廓誤差，如圖4所示。磨削采用CBN砂輪，砂輪半徑299.970 mm。磨削曲軸是來自上汽通用LTG發動機生產線，連桿頸直徑48.040 mm，偏心距49.000 mm[7]。

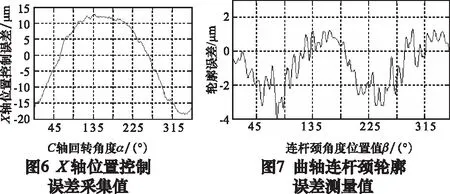
C軸和X軸位置控制誤差的采樣周期是4 ms，采集結果如圖5和圖6所示。曲軸磨削后，使用ADCOLE 1200SH綜合測量儀測量曲軸連桿頸輪廓誤差，測量數據經過截止頻率為50 UPR的高斯濾波，輪廓一周360°，測量1 440個點，測量結果如圖7所示。

3.2 由軸位置控制誤差計算曲軸輪廓誤差的結果

忽略數控曲軸隨動磨床砂輪架、砂輪和砂輪主軸的變形，C軸和X軸的位置控制信息等價于砂輪中心的軌跡信息。由于在測量曲軸連桿頸輪廓誤差時，使用了截止頻率為50 UPR的高斯濾波，因此在由軸位置控制誤差計算曲軸輪廓誤差時，為具更好的可比性，使用了相同的濾波處理。按照圖2方法計算的由C軸位置控制誤差和X軸位置控制誤差引起的曲軸輪廓誤差分別如圖8和圖9所示。

3.3 基于VMD的曲軸輪廓誤差分析結果

使用VMD進行曲軸輪廓誤差分解，必須提前確定分離的IMF數量K。根據第1部分的描述，曲軸輪廓誤差主要受到隨動磨床C軸和X軸的影響，因此將數量K設置為2，即將原始輪廓誤差實驗數據分解為2個分量，分解結果如圖10所示。

4 討論

4.1 基于VMD曲軸輪廓誤差分析結果討論

將圖10曲軸輪廓誤差VMD分析結果分別與圖8C軸位置控制誤差引起的輪廓誤差和圖9X軸位置控制誤差引起的輪廓誤差進行比較，明顯可以看出圖10中的IMF1分量、IMF2分量分別對應X軸位置控制誤差引起的輪廓誤差和C軸位置控制誤差引起的輪廓誤差。該對應關系可由圖11和圖12進行驗證，在圖11中IMF1分量基本上與X軸位置控制誤差引起的曲軸輪廓誤差相同，同樣在圖12中，IMF2分量基本上與C軸位置控制誤差引起的曲軸輪廓誤差相同。以上分析和討論表明，可以通過VMD曲軸輪廓誤差分析去預測隨動磨床C軸和X軸的性能或性能變化趨勢。

4.2 VMD和EEMD輪廓誤差分析方法比較

本文提出的基于VMD的輪廓誤差分析方法和作者在文獻[7]中提出的基于EEMD的輪廓誤差分析方法，雖然都能分離出與數控曲軸隨動磨床C軸和X軸相對應的分量，從而可以通過這些分離出的分量去分析判斷C軸和X軸的性能。兩種分析方法相互比較，VMD方法更加方便，更加快速，分解效果也更好。首先，VMD方法沒有EEMD方法的邊界效應問題和模態混疊問題，EEMD雖然是對EMD方法的改進并用于消除模態混疊，但從實際輪廓誤差的分析結果來看，并沒有完全消除。其次， EEMD需要在每步EMD之前添加高斯白噪聲，因此效率不如VMD。最后，VMD方法可以直接分離出對應C軸和X軸的輪廓誤差分量，而EEMD方法不僅在分解前需要對邊界做周期拓展，在分解后還需做一些后續的處理和高低頻分量的對比分析。

5 結語

本文給出了由數控隨動磨床C軸、X軸位置控制誤差計算曲軸連桿頸輪廓誤差的方法，為找出C軸、X軸位置控制誤差與曲軸輪廓誤差的對應關系提供了計算依據。

提出了基于VMD的輪廓誤差分析方法。通過磨削實驗，從數控系統中采集C軸和X軸位置控制誤差數據，并測量磨削后的曲軸連桿頸輪廓誤差數據。由采集的C軸和X軸位置控制誤差數據分別計算其對輪廓誤差產生的影響，作為進行輪廓誤差分析的對比依據。對測量的曲軸輪廓誤差數據進行基于VMD的輪廓誤差分析，獲得2個IMF分量。

將基于VMD的輪廓誤差分析結果與C軸和X軸位置控制誤差引起的輪廓誤差進行對比分析和驗證，得出的結論如下：IMF1分量對應的是X軸位置控制誤差引起的輪廓誤差，IMF2分量對應的是C軸位置控制誤差引起的輪廓誤差。將VMD方法和EEMD方法進行對比，基于VMD的輪廓誤差分析方法更方便，更快速，分解效果更好。

通過曲軸輪廓誤差分析，找出其各分量與數控隨動磨床C軸和X軸的對應關系，為從隨動磨削工件輪廓誤差預測機床關鍵功能部件性能提供了可能，可以作為關鍵功能部件預防性維護的依據。對于通過抽檢監控方式改進曲軸自動化生產線的效率和加工精度具有重要意義。