電勵磁直線同步電動機磁懸浮系統H∞魯棒控制的研究*

藍益鵬 張明慧

(沈陽工業大學電氣工程學院，遼寧 沈陽 110870)

傳統數控機床采用“旋轉電機+滾珠絲杠”的驅動系統，由于存在中間傳動裝置，不能夠滿足現代工業所要求的高加工精度[1]。

較傳統電機而言，直線電機沒有中間傳動環節、沒有沖擊、響應速度快、磨損和噪聲小，但是運動平臺和導軌之間存在較大的摩擦[2-4]。將電勵磁直線磁懸浮同步電動機作為數控機床驅動系統，其水平方向產生的推力和垂直方向產生的懸浮力使電動機實現直線進給和穩定懸浮，改善平臺和導軌間的摩擦。

但是電勵磁磁懸浮直線進給平臺系統具有較強的不穩定性，且在受到不確定性擾動或者端部效應等影響時，其參數也會發生變化，極大地增加了控制難度[5]。因此既要保證零傳動，又要實現高效、可靠的控制性能，是系統控制器的設計難點[6]。

H∞魯棒控制主要為了解決被控對象的不確定性擾動的問題，通過設計H∞魯棒控制器可以使系統有更好的穩定魯棒性和品質魯棒性。

正是如此，H∞魯棒控制也被許多學者相繼研究。文獻[7]設計了一種在非線性系統中執行器失效時H∞魯棒控制系統，但是它的抗擾能力和容錯能力有一定的范圍。文獻[8]提出混合H2/H∞魯棒預測控制器設計方法，使永磁同步伺服電機系統負載變化時起到更好的抑制擾動的作用和穩定性。文獻[9]則是基于線性矩陣不等式(LMI)設計了魯棒H∞滑模速度控制器和電流控制器，該控制系統能夠很好的抑制不確定性的外部擾動。

針對電勵磁直線電動機的磁懸浮系統，本文提出一種磁懸浮系統H∞魯棒控制方法，對電勵磁直線同步電動機懸浮系統方向的狀態空間模型進行線性化，將系統對擾動的不確定抑制問題歸為H∞控制問題，通過解Riccati不等式的正定解，得到懸浮系統的H∞魯棒控制器，并對其進行仿真研究。

1 電勵磁直線電動機的結構和運行機理

電勵磁直線電動機磁懸浮進給平臺主要由運動平臺，電勵磁直線同步電動機與輔助導軌組成。如圖1所示。

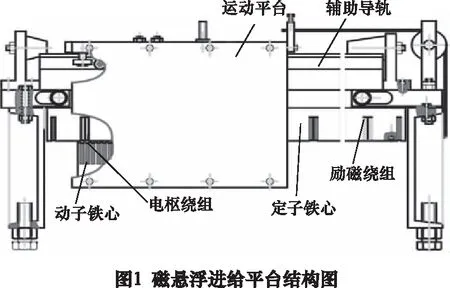
從圖1可知其運動平臺主要為兩部分：動子部分和定子部分。

(1)動子部分：動子鐵心和電樞繞組。在三相交流電的作用下，電樞繞組產生電樞磁場，從而產生電磁推力，推動平臺運行。

(2)定子部分：定子鐵心、勵磁繞組、輔助導軌以及端座組成。在直流電的作用下，勵磁繞組產生勵磁磁場，從而鐵心在磁場的作用下受到垂直向上的吸引力，吸引力與運動平臺重力相當時，可保證電機的穩定懸浮。

2 電勵磁直線電動機的數學模型

2.1 數學模型

在d-q軸坐標系下的電壓方程和磁鏈方程[10-11]。

電壓方程：

(1)

其中：ud、uq為電樞繞組d、q軸的電壓分量；uf為勵磁繞組的電壓；id、iq為d、q軸的電流分量；if為勵磁繞組電流；rs為電樞繞組電阻，rf為勵磁繞組電阻；v為運動平臺的運動速度，為極距；ψd、ψq為d、q軸的磁鏈；ψf為勵磁磁極磁鏈分量。

磁鏈方程:

(2)

其中：Lmd、Lmq為直軸與交軸的主電感；Lσ為電樞繞組漏感；Lσf為勵磁繞組漏感。

由電壓方程和磁鏈方程可將電勵磁直線電動機懸浮系統的數學模型描述為:

磁懸浮力方程：

(3)

(4)

(5)

懸浮方向的運動方程：

(6)

電壓方程：

(7)

式中：m為運動平臺的重量；δ為運動平臺實際懸浮的氣隙高度；fy為不確定性擾動；K1是磁懸浮系數，K1=5.659×10-6。

(8)

從式(8)可看出存在狀態變量之間的非線性。即電勵磁直線電動機磁懸浮系統是一個典型的非線性系統，由線性化后的線性模型可得到描述系統H∞魯棒控制的狀態空間模型。

2.2 模型的線性化

磁懸浮系統的模型線性化[13]：在系統平衡工作點對模型進行線性化，用泰勒公式在平衡點展開，忽略二階以后的高階項，從而得到一階數學模型，再采用傳統控制策略對其進行控制，借此取得良好的控制效果。所以本文在平衡點(i0,δ0)附近對磁懸浮系統進行線性化處理[14]。

Fy(i,δ)=Fy(i0,δ0)+KδΔδ+KiΔi

(9)

(10)

(11)

其中：

(12)

由式(9)～(11)可得

(13)

(14)

(15)

(16)

(17)

其中：A、B1、B2矩陣分別對應于式(16)中簡寫之后的矩陣；y為輸出，即觀測量等于系統的狀態變量；z為評價函數；C1和D12為加權系數矩陣；u為輸出；w為干擾。

3 H∞魯棒控制器的設計

由式(16)知磁懸浮系統具有不確定性的擾動。這種不確定的擾動在磁懸浮伺服系統中，將會降低磁場定向的精度，影響控制系統穩態和動態性能。為解決被控對象的不確定性擾動的問題，采用H∞魯棒控制，所以接下來將對電勵磁直線電動機進行H∞魯棒控制器的設計。

設系統增廣被控對象的狀態空間描述為

(18)

z=C1x+D12u

(19)

且rankD12=p，(A,B2)可穩定。即

(20)

由此設計懸浮系統狀態反饋控制器

u=Kx,K∈Rp×n

(21)

定理1[15]：對于給定的γ>0，存在狀態反饋矩陣K使得閉環系統(20)和(21)內部穩定且

‖Tzw(s)‖∞<γ

(22)

成立的充分必要條件是存在正定矩陣X>0滿足Riccati不等式

(23)

如果上述不等式有正定解X>0，則使閉環系統穩定且式(22)式成立的反饋陣由下式給出

(24)

由式(16)可知增廣被控對象中A、B1、B2矩陣分別為

(25)

(26)

(27)

加權系數矩陣C1和D12為：

(28)

(29)

式(28)和(29)中:q1、q2、q3、ρ為待取的加權系數。

所以由式(12)可計算得到

(30)

經過反復取試，C1和D12選擇如下：

(31)

(32)

之后利用MATLAB解Riccati不等式(23)，可得：

再由式(24)可以得到控制器的參數K如下所示：

(34)

4 仿真研究

電勵磁直線電動機控制系統的仿真框圖如圖2所示，系統的位置環節是H∞魯棒控制器，電流環用的是傳統PI控制器。

EELSM參數：電樞電阻Rs=1.2 Ω，直交軸電感Ld=Lq=0.018 74 H，直軸主電感Lmd=0.095 H，極距=0.048 m，極對數Pn=3，電機動子以及平臺質量M=10 kg，勵磁電流if=5.7 A。

用Simulink對所提的控制策略進行仿真研究，并與PI控制器進行對比。

(1)電勵磁直線同步電動機磁懸浮系統起動性能。

如圖3為電動機磁懸浮系統起動時的氣隙高度響應曲線。由圖可以得出：磁懸浮系統采用PI控制時，大約0.138 4 s穩定在系統給定氣隙高度，上升時間tr約為0.002 537 s，穩態誤差ess約8×10-7m，沒有超調；磁懸浮系統采用H∞魯棒控制時，大約0.072 46 s達到穩定值，上升時間tr約0.002 535 s，沒有穩態誤差，沒有超調。如圖4，磁懸浮系統采用H∞魯棒控制時，勵磁電流到達穩定比PI控制系統所需時間較短。由上述可得，H∞魯棒控制較PI控制系統來說，其到達穩定時間，上升時間，系統響應速度都比較快，動態性能和穩態性能都很好。

圖5為懸浮系統起動時高度誤差曲線，從圖中可以看出起動時PI控制的系統誤差為2.531×10-7m，H∞魯棒控制的響應速度快，系統誤差幾乎為0 m，可忽略不計。

(2)電勵磁直線同步電動機磁懸浮系統抗擾性能。如圖6和圖7，在0.3 s處突加15 N階躍擾動，之后在0.6 s去掉擾動，觀察其抗擾動性能。

如圖6為階躍擾動時氣隙高度曲線，從圖6中可以觀察出懸浮系統采用PI控制時，氣隙高度動態降落較大，大約6.0×10-5m，再次恢復到給定高度時間約為0.172 8 s；系統采用H∞魯棒控制時，系統氣隙高度降落約為1.6×10-5m，恢復到給定高度時間約0.05 s。由此可見H∞魯棒控制控制系統時，系統的抗擾性能更好。

圖7為階躍擾動時懸浮系統勵磁電流曲線，由圖7可以看出：PI控制時，加擾動之后，系統電流恢復時間約為0.02 s，且抖振較大；H∞魯棒控制加擾動之后系統電流恢復時間0.003 2 s，抖振較小。通過比較兩種控制方法，H∞魯棒控制抗擾動性能更好。

(3)電勵磁直線同步電動機磁懸浮系統對端部效應的抗擾性能。用正弦函數f=15sin(20t)N來模擬端部效應，在0.3 s處加入正弦擾動，觀察系統的抗擾能力。

圖8是懸浮系統加入正弦擾動時的氣隙高度曲線。由圖8可看出：系統采用PI控制在加正弦擾動后，振蕩比較大，抗擾能力差；采用H∞魯棒控制的系統沒有明顯的振蕩，跟隨性能較好，抗擾能力較PI控制有明顯的優越性。

圖9是懸浮系統加入正弦擾動時的氣隙高度誤差曲線。從圖9中可以觀察出PI控制的高度誤差很大，且加入正弦擾動之后波動較大；而H∞魯棒控制則氣隙高度誤差很小，并且擾動之后幾乎沒有波動，有較好的抗擾能力。

5 結語

針對電勵磁直線電動機磁懸浮系統，為提高其抗擾性能，提出一種H∞魯棒控制策略，得到結論如下：

(1)對EELSM的結構和懸浮系統的懸浮機理進行分析，由于電樞繞組交軸電流產生的磁場對定子鐵心的吸引力是隨負載的變化而變化的，具有不確定性，將其作為擾動處理之后，從而可得到含有不確定性擾動的磁懸浮力方程，進一步推導出磁懸浮系統的運動方程。

(2)針對推導所得而建立的系統狀態空間方程具有非線性，采用平衡點線性化的方法進行線性化處理，得到線性狀態空間方程。

(3)對磁懸浮控制系統中存在擾動的不確定性，提出用H∞魯棒控制策略抑制系統擾動，同時仿真結果表明H∞魯棒控制策略使系統具有更好的抗擾效果。