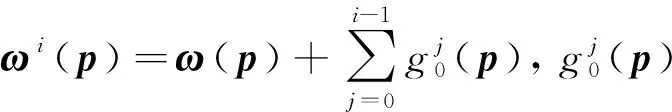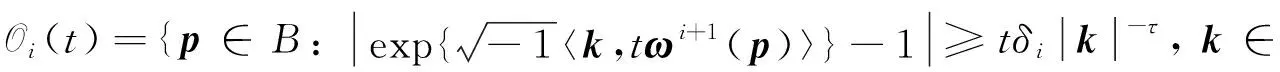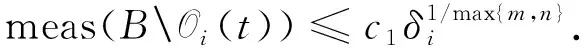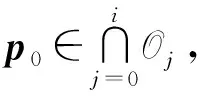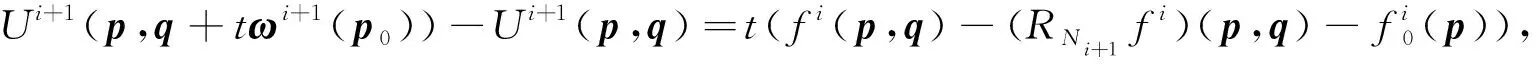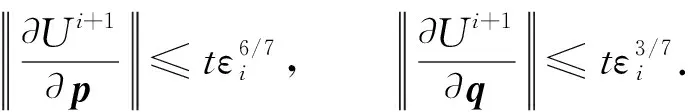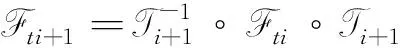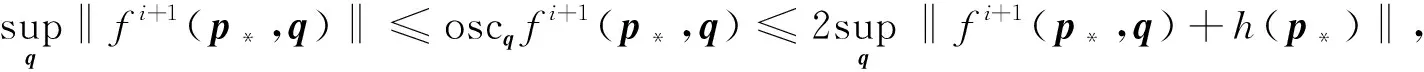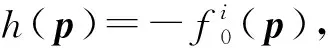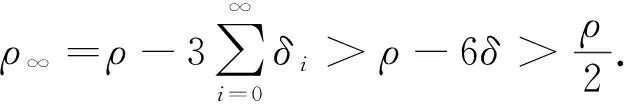高維小扭轉映射不變環面的存在性

李宏田, 所彧喬

(1. 中國刑事警察學院 基礎部, 沈陽 110854; 2. 長春理工大學 理學院, 長春 130022)

1 引言與主要結果

Moser[1]給出了作用變量和角度變量為1維情形下保體積映射的KAM定理, 該定理指出: 當擾動項足夠小時, 近可積保體積映射存在一族不變閉曲線. 該定理是KAM理論的三大基石之一[1-3]. 文獻[4-5]考慮含有一個作用變量、 多個角度變量的近扭轉映射, 給出了類似的KAM型定理. Cong等[6]得到了高維近可積映射的KAM型定理. 受上述工作啟發, 本文考慮作用變量和角度變量具有不同維數的小扭轉映射, 當映射滿足Rüssmann非退化條件及相交性條件時, 小扭轉映射存在一族不變環面. 該結論可用于Arnold-Beltrami-Childress流等保體積映射的誤差分析[7-8].

考慮映射Ft:B×Tn→m×Tn:

p1=p+tf(p,q),q1=q+tω(p)+tg(p,q),

(1)

其中B是m中的有界開集, Tn表示n維環面,t∈(0,1]為扭轉參數,ω(p),f(p,q)和g(p,q)于B×Tn上實解析.本文主要結果如下：

定理1若式(1)滿足如下條件:

(2)

(ii) 扭轉映射(1)于Bρ×Σρ上具有相交性質, 即對任意的p*∈Bρ, 均存在q*∈Σρ, 使得f(p*,q*)=0, 其中

Bρ={p∈m: Rep∈B, |Imp|<ρ},

Σρ={q∈n: Req∈Tn, |Imq|<ρ},

ρ>0為常數.

則存在ε>0, 使得當‖f‖+‖g‖<ε時, 對任意的t∈(0,1], 下列結論成立:

1) 近可積小扭轉映射(1)存在一族不變環面Tp(p∈B(ε,t)), 其頻率向量tω∞(p,t)關于t于(0,1]上一致滿足

|ω∞(p,t)-ω(p)|=O(ε);

2) 在(0,ε*]×(0,1]上, 不變環面測度的估計為

meas(BB(ε,t))=O(ε1/(7max{m,n}(n+τ+3))),

其中B(ε,t)為B的非空Cantor子集,ε*為某正常數.

本文用|·|和‖·‖分別表示歐氏范數和上確界范數.

2 引 理

引理1已知h(p,q)于Bρ×Σρ上實解析, 對于給定的p0∈D, 考慮定義于D×Σρ上的差分方程

V(p,q+tω(p0))-V(p,q)=t(h(p,q)-(RNh)(p,q)-h0(p)),t∈(0,1],

(3)

其中D={p: |p-p0|0為給定的常數,

表示h(p,q)的Fourier級數形式的N-1階截斷項的余項,V(p,q)待定.若ω(p0)滿足帶參數的Diophantus條件:

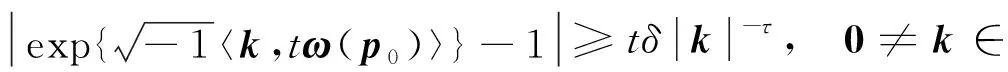
(4)

則式(3)有且僅有一個滿足V0(p)=0的實解析解V(p,q), 其中:δ>0;τ>(max{m,n}+1)×max{m,n}-1; (p,q)∈D×(Σρ-δ), 0<δ<ρ,Σρ-δ={q∈Σρ: dist(q,?Σ)≥δ}, 滿足

c0={22n-2}π2(n+τ+1)n+τ+1exp{-(n+τ+1)}/3.

證明: 因為V0(p)=0, 不妨設V(p,q)具有如下Fourier級數形式

由式(3)得

由Cauchy積分公式及式(4), 當(p,q)∈D×(Σρ-δ)時, 有

3 KAM迭代

設式(1)的頻率向量及擾動項于Dρ×Σρ上滿足:

‖f‖+‖g‖<ε,

(5)

(6)

其中M0為常數,ε足夠小.設i=0,1,…, 定義迭代參數如下:

j=0,1,…,i-1.記

Di={p∈Bρ: |p-p0|

設

(7)

其中c1,c2,…表示與擾動參數ε、 扭轉參數t以及迭代步驟i無關的正常數.

因為t為小扭轉參數, 所以不失一般性, 可簡記ωi(p,t),fi(p,q,t),gi(p,q,t)為ωi(p),fi(p,q),gi(p,q).設在第i次迭代中, 映射(1)轉化為Fti:

p1=p+tfi(p,q),q1=q+tωi(p)+tgi(p,q),

(8)

其擾動項滿足

‖fi‖+‖gi‖<εi,

故存在常數M0, 使得

‖ωi‖≤2ε

(9)

定義

由文獻[6], 關于其測度有如下估計:

(10)

定義Di+1×Σi+1上的坐標變換Ti+1:

p1=p+Ui+1(p,q),q1=q+Vi+1(p,q).

(11)

(12)

p1=p+tfi+1(p,q),q1=q+tωi+1(p)+tgi+1(p,q),

(14)

其中Ui+1,Vi+1待定, 其新的擾動項

(17)

(18)

(19)

(20)

由式(17),(19)知

(21)

由式(13)知

(22)

(23)

由文獻[3]中的引理以及截斷項Ni+1的選取, 對式(24)中的最后一項, 有如下估計:

‖RNi+1fi‖≤ε9/7.

(25)

于是, 關于新擾動項, 有

同理

(27)

由式(26),(27)知,

(28)

取Li=T1°T2°…°Ti, 于是Fi=Li-1°Ft°Li.在Di×Σi上, 設變換Li為

p1=p+Pi(p,q),q1=q+Qi(p,q),

(29)

則

p1=p0,q1=q+tω∞(p0,t),

(30)

|ω∞(p0,t)-ω(p0)|≤2ε.

至此完成了定理1的證明.