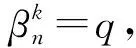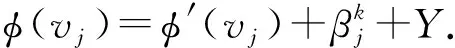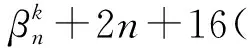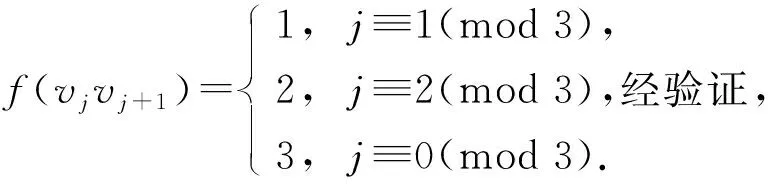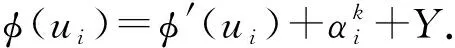聯(lián)圖的鄰點全和可區(qū)別全染色

崔福祥, 楊 超, 葉宏波, 姚 兵

(1. 上海工程技術(shù)大學(xué) 數(shù)理與統(tǒng)計學(xué)院, 智能計算與應(yīng)用統(tǒng)計研究中心, 上海 201620; 2. 西北師范大學(xué) 數(shù)學(xué)與統(tǒng)計學(xué)院, 蘭州 730070)

1 引言與預(yù)備知識

定義1設(shè)f:V(G)∪E(G)→{1,2,…,k}是圖G的一個正常k-全染色.令權(quán)值

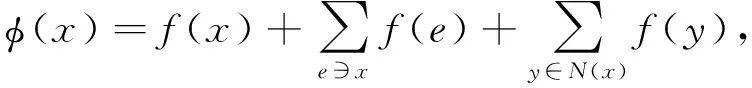
其中N(x)={y∈V(G)|xy∈E(G)}.對任意的邊uv∈E(G), 如果φ(u)≠φ(v)成立, 則稱f是圖G的一個鄰點全和可區(qū)別k-全染色.圖G的鄰點全和可區(qū)別全染色中最少的顏色數(shù)稱為G的鄰點全和可區(qū)別全色數(shù), 記為ftndi∑(G).

定義2設(shè)圖Gm,Gn為互不相交的簡單連通圖, 若其同時滿足如下兩個條件:

1)V(Gm∨Gn)=V(Gm)∪V(Gn);

2)E(Gm∨Gn)=E(Gm)∪E(Gn)∪{uv|u∈V(Gm),v∈V(Gn)}.

則稱圖Gm∨Gn為Gm和Gn的聯(lián)圖.

設(shè)V(Gm)={ui|1≤i≤m},V(Gn)={vj|1≤j≤n}.由聯(lián)圖Gm∨Gn的定義知, 要驗證一個正常全染色f為Gm∨Gn的一個鄰點全和可區(qū)別全染色, 需下述3個條件同時成立:

(i)φ(ui)≠φ(ui+1), 1≤i≤m-1;

(ii)φ(vj)≠φ(vj+1), 1≤j≤n-1;

(iii)φ(ui)≠φ(vj), 1≤i≤m, 1≤j≤n.

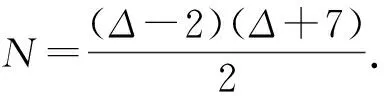
本文確定了路與路、 路與圈、 圈與圈三類聯(lián)圖的鄰點全和可區(qū)別全色數(shù).

2 主要結(jié)果

由定義1和定義2知, 圖G的一個鄰點全和可區(qū)別全染色也是圖G的一個正常全染色, 從而有：

引理1設(shè)G是一個階數(shù)至少為3 的簡單連通圖, 則ftndi∑(G)≥Δ(G)+1.

定理1設(shè)Pm和Pn分別表示階數(shù)為m和n的兩條路(m≥n≥3), 則當m=n時, ftndi∑(Pm∨Pn)≤Δ+2, 當m≠n時, ftndi∑(Pm∨Pn)=Δ+1.

證明: 設(shè)路Pm=u1u2…um, 路Pn=v1v2…vn.下面分兩種情形討論.

情形1) 當m=n時, 定義Pm∨Pn的一個(Δ+2)-全染色f1如下:

聯(lián)邊uivj的染色f1(uivj)由下列邊染色矩陣確定:

其中i∈[1,m],j∈[1,n].

①n≡1(mod 2).

由染色f1, 易知Φ(ui)={8,9,13,14},Φ(vj)={6,7,11,12}.顯然, 連通分支Pm中的相鄰頂點以及連通分支Pn中的相鄰頂點的權(quán)值都是可區(qū)別的, 因此下面只需證聯(lián)圖G中相鄰頂點ui和vj的權(quán)值不同即可.因為

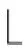
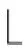
故當n>3時,φ(ui)<φ(vj).當n=3時, 保持上述染色方案不變, 經(jīng)驗證也滿足G中相鄰頂點ui與vj的權(quán)值不同.故ftndi∑(Pm∨Pn)≤Δ+2.

②n≡0(mod 2).

由染色f1可得Φ(ui)={8,13,14},Φ(vj)={6,11,12}.顯然, 在連通分支Pm中的相鄰頂點和Pn中的相鄰頂點的權(quán)值都是可區(qū)別的, 因此下面只需證聯(lián)圖G中相鄰頂點可區(qū)別即可.因為

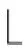
故當n>4時,φ(ui)<φ(vj).當n=4時, 調(diào)整分支Pn的邊染色, 使得f(v1v2)=f(v3v4)=4,f(v2v3)=3, 則可得G中相鄰頂點ui與vj的權(quán)重不同, 從而可得ftndi∑(Pm∨Pn)≤Δ+2.

情形2) 當m>n時, 定義Pm∨Pn的一個(Δ+1)-全染色f2如下:

聯(lián)邊uivj的染色f2(uivj)由下列邊染色矩陣確定:

其中i∈[1,m],j∈[1,n].

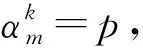
αk={p-k,p-2k,…,p-nk,p+n(1-k),p+n(2-k),…,p},

且αk中的元素滿足

① 計算路Pm中各頂點的權(quán)值φ′(ui)和φ(ui):

φ′(u1)=12,φ′(um-1)=2m+12.

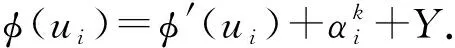
可得k=9, 即當m=n+9時,φ(u1)=φ(u2).當2≤i≤m-2時, 若i=n, 此時當n≤m-3時, 若φ(un)=φ(un+1), 則

無解； 當n=m-2時, 若φ(un)=φ(un+1), 則由

得m=n+3, 即當m=n+3時,φ(um-1)=φ(um-2).若i

可得n=m+4(或m+3)>m, 矛盾.

綜上可知, 對于路Pm中任意相鄰頂點ui和ui+1, 均有φ(ui)≠φ(ui+1), 且max{φ(ui)}=φ(um-2)(或φ(um-1)).

② 計算路Pn中各頂點的權(quán)值φ(vj):

φ(v1)=φ(vn)=6+2β.

當2≤j≤n-1時,

顯然, 對于路Pn中任意相鄰頂點vj和vj+1, 均有φ(vj)≠φ(vj+1), 且min{φ(vj)}=6+2β.

當m≥4時, 有m2-3m>0, 故對任意的ui∈V(Pm),vj∈V(Pn), 均有φ(ui)<φ(vj).當max{φ(ui)}=φ(um-1)時有

當m≥4時, 有m2-m-6>0, 故對任意的ui∈V(Pm),vj∈V(Pn), 均有φ(ui)<φ(vj).

綜上可知, 對任意頂點ui∈V(Pm),vj∈V(Pn), 均有φ(ui)≠φ(vj).證畢.

定理2設(shè)Pm和Cn分別表示階數(shù)為m和n的路和圈(m,n≥3), 則

且當m=n≠1(mod 2) 時, ftndi∑(Pm∨Cn)≤Δ+2.

證明: 設(shè)路Pm=u1u2…um, 圈Cn=v1v2…vnv1, 則Pm∨Cn=Pm∨Pn∪{v1vn}.下面分3種情形討論.

情形1) 當m=n≠1(mod 2) 時, 定義Pm∨Cn的一個(Δ+2)-全染色g1如下:

g1(v1vn)=4;

g1(uivj)=f1(uivj), 1≤i≤m, 1≤j≤n;

g1(x)=f1(x),x∈{ui,vj,uiui+1,vjvj+1|1≤i≤m, 1≤j≤n}.

由染色g1得Φ(ui)={8,13,14},Φ(vj)={11,12}.顯然, 在連通分支Pm中相鄰頂點和Cn中相鄰頂點的權(quán)重都是鄰和可區(qū)別的, 因此下面僅需證聯(lián)圖G中相鄰頂點ui與vj的權(quán)值不同即可.又因為

所以當n≥3時,φ(ui)<φ(vj), 故ftndi∑(Pm∨Cn)≤Δ+2.

情形2) 當m>n且n≠1(mod 3)時, 定義Pm∨Cn的一個(Δ+1)-全染色g2如下:

g2(v1vn)=m+3;

g2(uivj)=f2(uivj), 1≤i≤m, 1≤j≤n;

g2(x)=f2(x),x∈{ui,vj,uiui+1,vjvj+1|1≤i≤m, 1≤j≤n}.

① 路Pm中各頂點的權(quán)值φ′(ui)和φ(ui)同定理1中情形2)的①.

② 計算圈Cn中各頂點權(quán)值φ(vj):

φ(vn)=m+10+2β.

當2≤j≤n-1時,φ(vj)同定理1中情形2)的②.顯然, 對于圈Cn中任意相鄰頂點均有φ(vj)≠φ(vj+1), 且min{φ(vj)}=9+2β.

當n≥3時, 有m2-3m+6>0.故對任意頂點ui∈V(Pm),vj∈V(Cn), 均有φ(ui)≠φ(vj).當max{φ(ui)}=φ(um-1)時, 有

當n≥3時, 有m2-m>0.故對任意頂點ui∈V(Pm),vj∈V(Cn), 均有φ(ui)≠φ(vj).

綜上可知, ftndi∑(Pm∨Cn)=Δ+1.

情形3) 當m

聯(lián)邊uivj的染色g3(uivj)由下列邊染色矩陣確定：

其中i∈[1,m],j∈[1,n].

βk={q-k,q-2k,…,q-mk,q+m(1-k),q+m(2-k),…,q},

且集合中元素滿足

① 計算路Pm中各頂點權(quán)值φ(ui):

φ(u1)=φ(um)=6+2α.

當2≤i≤m-1時,

顯然, 對于路Pm中任意相鄰頂點均有φ(ui)≠φ(ui+1), 且min{φ(ui)}=6+2α.

② 計算圈Cn中各頂點權(quán)值φ′(vj)和φ(vj):

φ′(v1)=n+19,φ′(vn-1)=2n+12.

可得m=2n-2, 又m

無解; 當m=n-2時, 若φ(vm)=φ(vm+1), 則由

得n=m+3, 即當n=m+3時,φ(vm)=φ(um+1).若j

綜上可知, 對于圈Cn中任意相鄰頂點vi和vj+1, 均有φ(vj)≠φ(vj+1), 且有max{φ(vj)}=φ(vn-2)(或φ(vn)).

當n≥4時, 有n2-n-4>0, 故對任意ui∈V(Pm),vj∈V(Cn), 均有φ(ui)<φ(vj).

當max{φ(vj)}=φ(vn-2)時, 有

故對任意ui∈V(Pm),vj∈V(Cn), 均有φ(ui)<φ(vj).

綜上可知, 對任意頂點ui∈V(Pm),vj∈V(Cn), 均有φ(ui)≠φ(vj).證畢.

定理3設(shè)Cm和Cn分別表示階數(shù)為m和n的兩個圈(m≥n≥3), 則

且當m=n≠1(mod 2)時, ftndi∑(Cm∨Cn)≤Δ+2.

證明： 設(shè)圈Cm=u1u2…umu1, 圈Cn=v1v2…vnv1, 則Cm∨Cn=Pm∨Pn∪{u1um,v1vn}.下面分兩種情形討論.

情形1) 當m=n≠1(mod 2)時, 定義Cm∨Cn的一個(Δ+2)-全染色h1如下:

h1(u1um)=2；

h1(v1vn)=4；

h1(uivj)=f1(uivj), 1≤i≤m, 1≤j≤n;

h1(x)=f1(x),x∈{ui,vj,uiui+1,vjvj+1|1≤i≤m, 1≤j≤n}.

由染色h1可得Φ(ui)={13,14},Φ(vj)={9,10}.顯然, 連通分支Cm中的相鄰頂點以及連通分支Cn中的相鄰頂點的權(quán)值都是可區(qū)別的, 因此下面只需證聯(lián)圖G中相鄰頂點ui與vj的權(quán)值不同即可.又因為

故當n≥4時,φ(ui)<φ(vj), 即ftndi∑(Cm∨Cn)≤Δ+2.

情形2) 當m>n且n≠1(mod 3)時, 定義Cm∨Cn的一個(Δ+1)-全染色h2如下:

h2(u1um)=h2(v1vn)=m+3;

h2(uivj)=f2(uivj), 1≤i≤m, 1≤j≤n;

h2(x)=f2(x),x∈{ui,vj,uiui+1,vjvj+1|1≤i≤m, 1≤j≤n}.

① 計算圈Cm中各頂點權(quán)值φ′(ui)和φ(ui):

φ′(u1)=m+19.

可得m<2, 矛盾.故φ(u1)≠φ(u2).當2≤i≤m-2時,φ′(ui)和φ(ui)同定理1的情形2)中2≤i≤m-2的情形.若φ(um-1)=φ(um), 則由

得n<0, 矛盾.若φ(um)=φ(u1), 則由

可得m<3(或m<2), 矛盾.

與上述證明過程類似, 當m=n+3時, 調(diào)整染色方案, 令

經(jīng)驗證調(diào)整后的染色是Cm∨Cn的一個鄰點全和可區(qū)別全染色.

綜上可知, 對于圈Cm中任意相鄰頂點ux,uy, 均有φ(ux)≠φ(uy), 且max{φ(ui)}=φ(um-2)(或φ(um)).

② 計算圈Cn中各頂點權(quán)值φ(vj):

當2≤j≤n-1時,φ(vj)同定理1中情形2)的②.顯然, 對于圈Cn中任意相鄰頂點vx,vy, 均有φ(vx)≠φ(vy), 且min{φ(vj)}=9+2β.

當m≥4時, 有m2-3m+6>0.故對任意的ui∈V(Cm),vj∈V(Cn), 均有φ(ui)≠φ(vj).當max{φ(ui)}=φ(um)時, 有

當m≥4時, 有m2-m-10>0, 故對任意的ui∈V(Cm),vj∈V(Cn), 均有φ(ui)≠φ(vj).

綜上可知, ftndi∑(Cm∨Cn)=Δ+1.證畢.