基于仿射不變塊相似度量的BM3D圖像去噪算法
徐華平, 賈小寧
(長春理工大學 數學與統計學院, 長春 130022)
圖像在采集和傳輸過程中可能受各種噪聲的干擾, 由于噪聲的存在會降低圖像的質量, 從而影響與圖像處理有關的應用, 如圖像分析、 邊緣檢測、 模式識別和目標監測等. 因此, 圖像去噪[1-3]目前已成為計算機視覺領域中的重要課題, 受到廣泛關注. 目前, 基于塊的方法[4-8]廣泛應用于最新的圖像去噪算法中. BM3D(block matching and 3D filtering)[4]算法是目前公認最好的去噪方法[9-10]之一, 其通過相似塊群的協同過濾[11], 將空間自相似與頻域閾值相結合. 但用規則的方形塊去噪可能會在圖像邊緣產生偽影. 為去除這些偽影, 文獻[12]提出了用幾種不同形狀(圓、 半圓、 1/4圓)代替正方形塊, 并結合使用無偏風險估計進行估算. 在塊匹配中, 若圖像受到仿射形變, 使用正方形塊尋找到相似塊的數量將會減少, 使在塊匹配過程中無法獲得足量的相似塊, 從而降低圖像在變換域中的稀疏性, 進而降低算法的去噪性能.
針對上述問題, 本文提出一種基于仿射不變塊相似度量的BM3D圖像去噪(Affine-BM3D)算法, 該算法有效利用了圖像中存在的仿射不變自相似性[13-18]. 在塊匹配中, 先使用橢圓塊進行塊匹配, 再運用仿射不變塊相似度量[19-21]計算兩個塊的距離, 能尋找到更多的相似塊, 將其用于圖像去噪, 從而取得較好的去噪效果, 并克服了偽影和相似塊數量減少的問題.
1 仿射不變塊相似度量
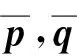
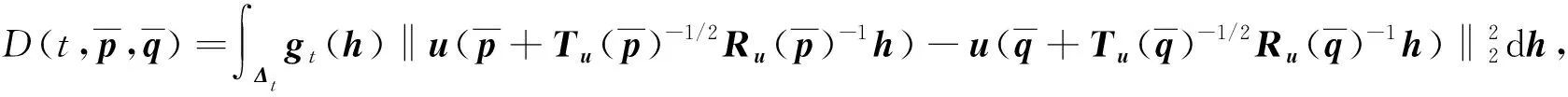
(1)
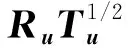
1.1 計算橢圓塊Bu和結構張量Tu
文獻[20]提出了計算結構張量和橢圓塊的方法, 其計算方法為
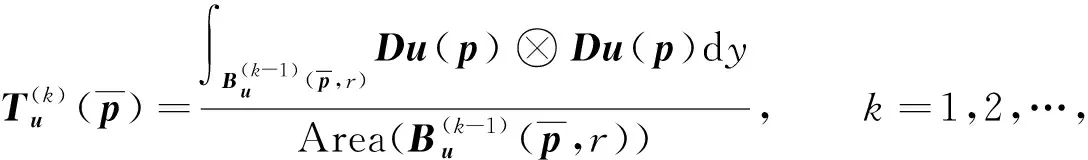
(2)
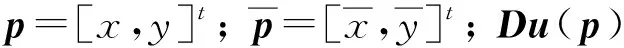
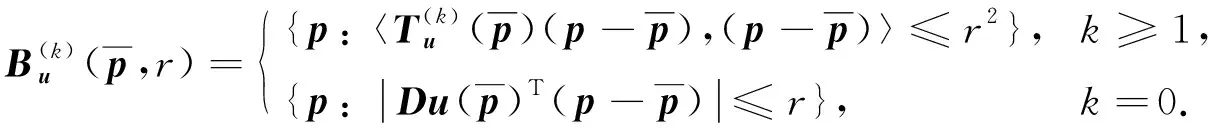
(3)
該迭代算法的實現步驟如下.


(4)
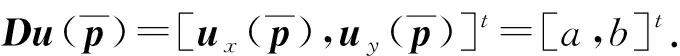
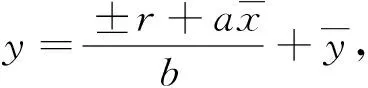
(5)
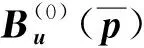

(6)
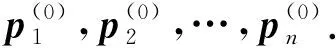
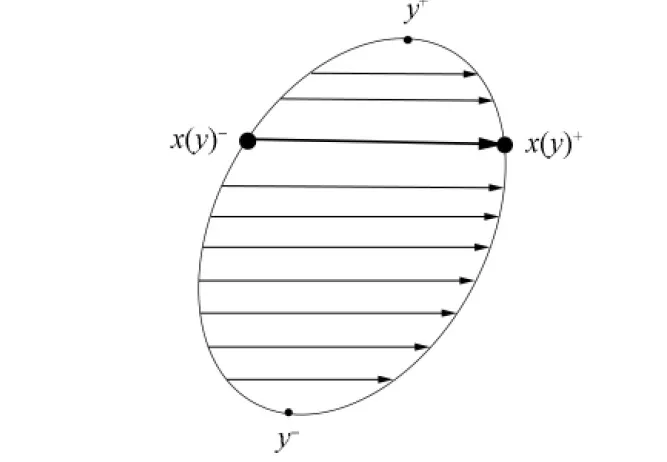
圖1 遍歷橢圓塊的示意圖Fig.1 Schematic diagram of traversing of elliptical patches
下面計算初始橢圓塊中心點的結構張量.由式(2)可知, 一個中心點的結構張量等于橢圓塊內點的梯度張量積的累加和再除以塊內點的個數.梯度張量積[22]的計算公式為
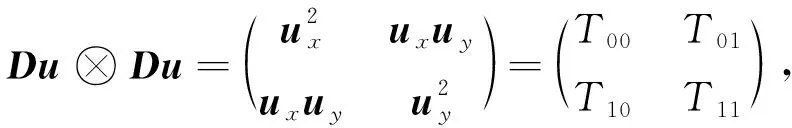
(7)


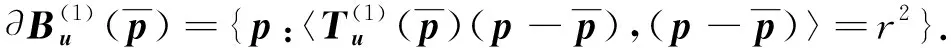
(8)
由式(8)可解得兩個極點的y坐標為
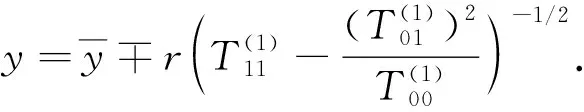
(9)
遍歷兩個極點之間的每一行, 計算出每行與橢圓塊邊界(8)兩個交點的x坐標為

(10)

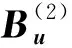
通過上述方法迭代, 最終得到中心點的一個結構張量及與該結構張量有關的橢圓塊.
1.2 計算主方向和旋轉變換
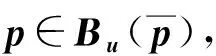
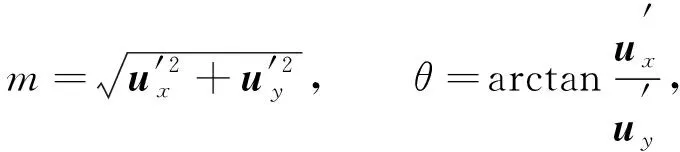
(11)

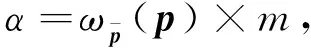
(12)
其中

(13)


(14)
其中θ是給定的主方向.
1.3 歸一化橢圓塊和插值
通過上述操作得到了中心點的結構張量和相應的旋轉變換矩陣, 因此, 可通過公式

(15)
計算出仿射變換, 即將橢圓塊歸一化為相同半徑的圓形塊, 如圖2所示.通過比較兩個大小相同的圓形塊, 可直觀地計算出它們之間的距離.

圖2 橢圓塊和圓形塊轉換示意圖Fig.2 Schematic diagram of transformation of elliptical patch and circular patch
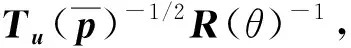
經過以上三步處理, 得到所需變量的數值, 最后再利用度量公式(1)進行計算, 得出兩個塊之間的距離.
2 算法設計
Affine-BM3D算法分為基本估計階段和最終估計階段. 每個階段又可分為3個步驟.
1) 橢圓塊塊匹配分組: 使用橢圓塊在搜索窗口中尋找相似塊, 并且使用仿射不變塊相似度量計算兩個塊之間的距離, 將相似的橢圓塊分為一組.
2) 協同濾波: 在基本估計階段使用硬閾值濾波去除大量噪聲; 在最終估計階段使用Wiener濾波進一步去除噪聲, 同時恢復邊緣紋理.
3) 聚合: 對估計值加權平均得到最終的估計值.
Affine-BM3D算法流程如圖3所示.
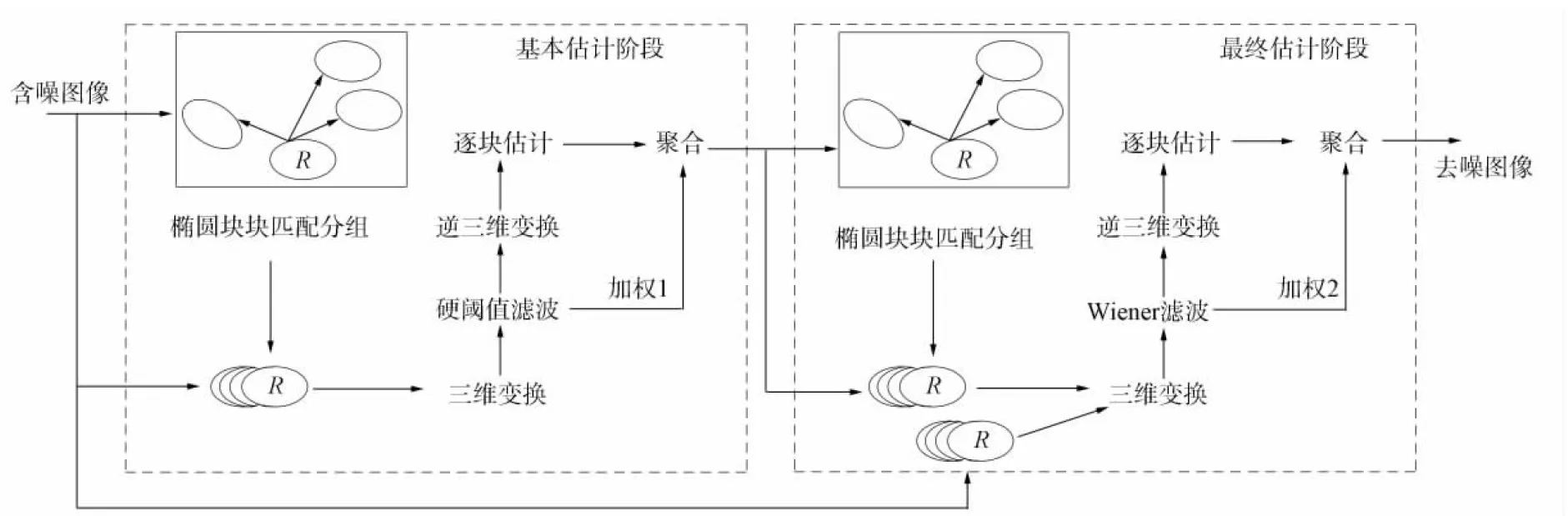
圖3 Affine-BM3D算法流程Fig.3 Flow chart of Affine-BM3D algorithm
2.1 橢圓塊塊匹配分組
在一個正方形搜索窗口內, 設窗口大小為w, 以參考點x為中心的橢圓塊, 遍歷窗口內所有其他點, 對于每個點, 計算出以其為中心的橢圓塊, 再逐個比較是否與參考塊相似.
對于比較兩個橢圓塊是否相似, 首先需將兩個橢圓塊歸一化為半徑大小相同的圓形塊.在該歸一化過程中, 先計算橢圓塊中心點的結構張量, 再確定與每個橢圓塊相關的主方向, 計算出相應的旋轉變換, 然后計算出它們之間的仿射變換進行歸一化.歸一化后圓形塊上點的像素值均未知, 通過插值求出估計值, 再用仿射不變塊相似度量計算出兩個塊之間的距離.如果待匹配塊與參考塊的距離小于給定的閾值, 則認為是參考塊的相似塊, 然后將相似的橢圓塊分為一組, 形成一個三維陣列.如圖4所示,R為參考塊, 圖中其他黑色虛線橢圓塊為與其相似的塊.
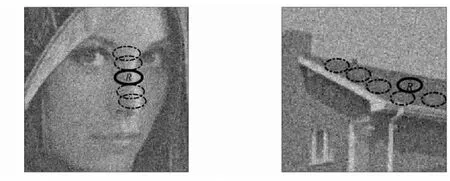
圖4 相似橢圓塊組示意圖Fig.4 Schematic diagram of similar elliptical patches groups
2.2 協同濾波
對于三維相似橢圓塊群組, 協同濾波過程如下:
1) 對三維橢圓塊群組進行三維線性變換;
2) 收縮變換域系數以減小噪聲, 如基本估計階段使用硬閾值濾波, 最終估計階段使用Wiener濾波;
3) 利用三維逆變換得到所有橢圓塊群組的估計值.
2.3 聚 合
在聚合過程中, 對于三維逆變換后的同一個相似橢圓塊會有多個估計值, 需要對每個估計值計算加權平均值, 以得到圖像的最終估計值.
3 仿真實驗分析
為驗證Affine-BM3D算法的性能, 本文選擇灰度測試圖像進行主觀和客觀指標的評價. 主觀上, 通過視覺觀察一些可視特點, 包括邊緣保持能力和模糊程度等對Affine-BM3D算法的性能進行評價; 客觀上, 視覺評估可通過峰值信噪比(peak signal to noise ratio, PSNR)和結構相似度(structural similarity, SSIM)等對Affine-BM3D算法的性能進行評價.
3.1 圖像質量評價指標
本文采用PSNR作為評價指標驗證本文算法:
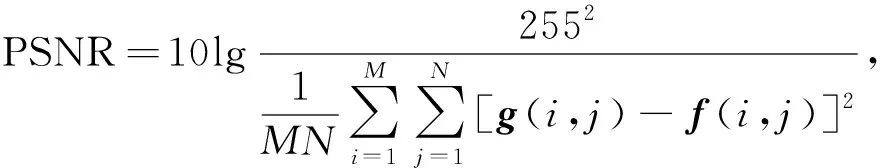
(16)
其中g(i,j)表示去噪圖像,f(i,j)表示原始圖像,M,N表示圖像大小.
3.2 實驗結果與分析
3.2.1 多噪聲水平下圖像去噪實驗
下面通過仿真實驗驗證Affine-BM3D算法的性能, 選取常見的8張自然圖像作為實驗圖像, 如圖5所示. 選取3種算法作為對比算法, 包括非局部均值算法(non-local means algorithm, NLM)、 仿射非局部均值算法(affine non-local means algorithm, Affine-NLM)和BM3D算法. 4種算法均采用MATLAB R2018b實現, 計算平臺為dell-PC Intel(R) Xeon(R) CPU E5-2620v4@2.10 GHz, 2.10 GHz, 32 GB內存的計算機.

圖5 實驗中使用的無噪聲圖像Fig.5 Noise-free images used in experiment
模擬噪聲標準差為10,20,30,40這4種情形, 實驗所得4種算法的PSNR值列于表1~表4. 由表1~表4可見, 在低噪聲的情形下, 本文算法的PSNR值比BM3D的值略小, 但相差不大; 但在高噪聲水平下, 本文算法總是優于BM3D算法.

表1 模擬噪聲標準差為10時4種算法的PSNR值

表2 模擬噪聲標準差為20時4種算法的PSNR值

表3 模擬噪聲標準差為30時4種算法的PSNR值

表4 模擬噪聲標準差為40時4種算法的PSNR值
圖6和圖7為噪聲σ=20時, 本文算法與其他3種算法的去噪效果對比結果. 由圖6和圖7可見, 本文算法的去噪效果優于BM3D算法和其他算法. 圖8為采用本文算法對不同程度含噪的Lena 圖像進行去噪的結果. 由圖8可見, 本文算法較好地去除了圖像中的噪聲, 還原了原圖像.

圖6 不同算法對House,Lena,Girl和Dice圖像的去噪效果Fig.6 Denoising effects of House, Lena, Girl and Dice images by different algorithms
在計算時間方面, 本文算法比BM3D算法慢, 原因如下: 1) 計算橢圓塊較耗時, 對于計算一個橢圓塊, 需要迭代計算多次, 使橢圓塊與其中心點的結構張量減少了對初始區域的依賴性; 2) 相似橢圓塊的尋找和匹配上較耗時.

3.2.2 高噪聲水平下圖像去噪實驗
為進一步驗證本文算法在高噪聲情形下去噪的有效性及優勢, 使用如圖9所示常用的12張自然圖像(Set12 dataset)作為測試集進行驗證. 測試兩種不同的高噪聲水平σ=30和σ=40, 并將去噪結果與NLM,Affine-NLM和BM3D算法進行比較, 結果列于表5. 由表5可見, 在高噪聲情形下本文算法的去噪效果普遍更佳, 其PSNR值普遍高于其他算法. 例如, 在針對σ=30的噪聲水平去噪時, 大部分圖像的去噪效果優于原始的BM3D算法.
綜上所述, 本文針對偽影和相似塊數量減少的問題, 提出了一種基于仿射不變塊相似度量的BM3D圖像去噪算法. 在塊匹配過程中, 該算法使用橢圓塊而不是規則的正方形塊, 并且使用仿射不變塊相似度量計算兩個塊之間的距離, 這種相似度量能比較與仿射變換有關的塊. 實驗結果表明, 本文算法提高了去噪效果, 在主觀視覺方面獲得了良好的效果. 在PSNR方面, 也有較強的優勢.

圖9 12張測試圖像Fig.9 Twelve test images
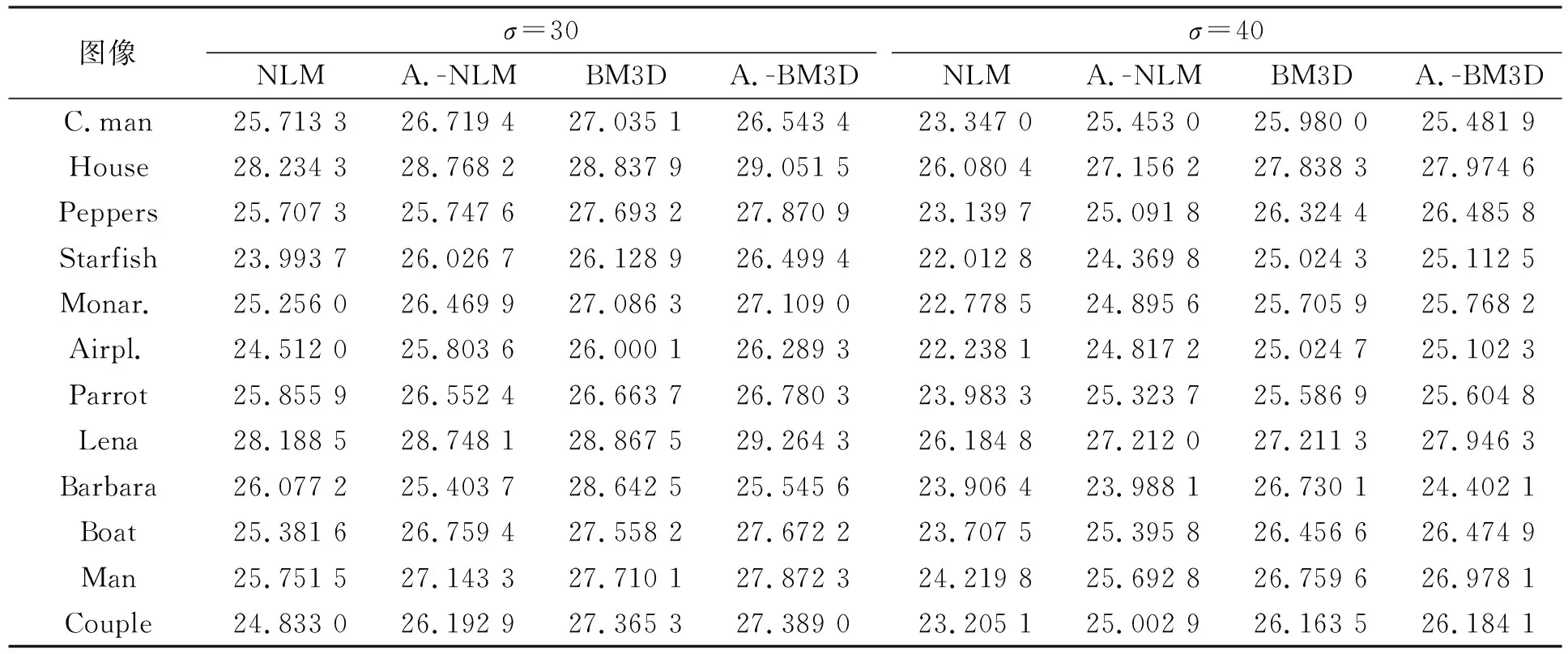
表5 不同算法對12張測試圖像去噪后的PSNR結果

