落實數學抽象素養為本的概念教學
——以“函數的單調性”教學為例
浙江省安吉縣孝豐高級中學 (313300) 黃 鋒
當代世界著名數學家、菲爾茲獎的獲得者M·F·阿蒂亞曾經提出:要處理復雜性驟增的數學問題,就必須建立和發展相應的抽象數學概念.而任何概念的形成都要經歷抽象到科學抽象再到數學抽象三個過程,那么從抽象到數學抽象如何在教學中落實到位呢?筆者以《函數的單調性》第一課為例,談談如何在概念課教學中落實“數學抽象”這一核心素養的實踐與思考.
1.數學抽象的抽象過程
數學的概念和形式都呈現出高度的抽象性,對于高度抽象化的數學概念的引入,一定從生活中真實的事物出發[1].教科書中函數單調性的引入雖然是以具體函數的圖像形象的切入,但是它的高度抽象,學生很難理解.因此在教學中,應注重引導學生充分經歷這個抽象過程,通過思考、討論、探究,理解單調性的含義、感受“任意”的思想.筆者認為“函數單調性”從抽象到數學抽象的抽象過程需要經歷三個步驟.
1.1 抽象的具體化生成了抽象的定性化
函數是描述事物變化規律的數學模型,因此我們可以通過研究函數的性質獲得對客觀世界中事物變化規律的認識,通過研究函數值隨自變量值的變化規律,可以獲得函數所刻畫的現實問題的變化規律.
教學片段1創設情境,引入課題
觀察下列圖片,回答如下問題:
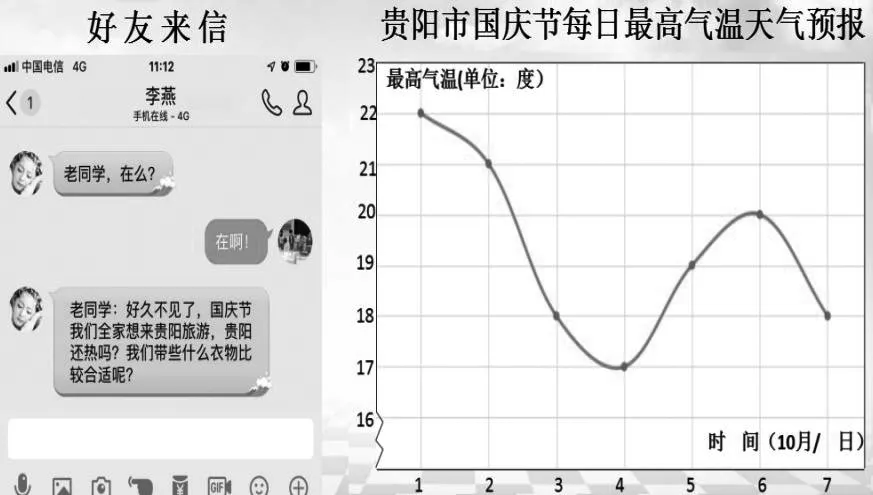
圖1
問題1 你能結合天氣預報給我的好朋友一些建議嗎?
問題2 如果把時間設為x,最高氣溫設為y,y是x的函數嗎?
問題3 如果y是x的函數,那么函數圖像反映了哪些變化規律?
設計意圖:以生活實例為情景,激發學生的學習興趣,通過問題2,體現數學建模過程,培養學生建模意識,通過問題3,讓學生直觀感知圖像“上升(下降).
教學片段2對比分析 定性刻畫
觀察下列函數圖像,回答如下問題:
問題4 比較圖2和圖3,它們函數圖像分別具有什么樣的變化趨勢?
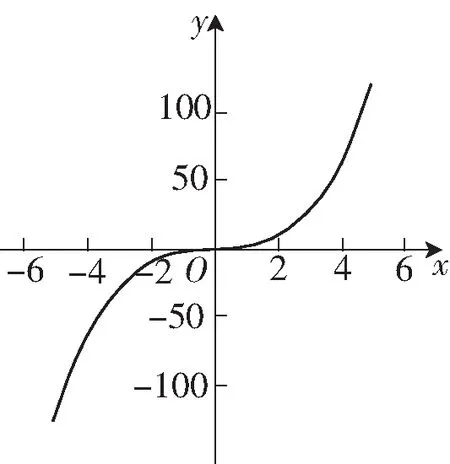
圖2
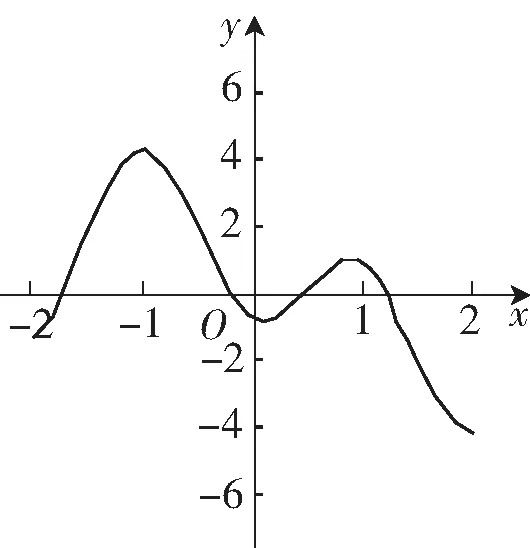
圖3
生:圖2特點是函數圖像從左到右保持上升趨勢,圖3特點是圖像從左到右有升也有降.
問題5 圖2對應的函數圖像“從左到右保持上升趨勢”,這一不變性是函數的什么性質呢?
師:從左到右函數值有什么變化呢?
生:增大.
師:函數值隨著誰的變化而增大呢?
生:y隨著x的增大而增大(減小).
師:在初中,我們把這樣的性質稱為函數的單調性.
問題6 對比圖3和圖4,這兩個函數具有什么樣的共同特點?
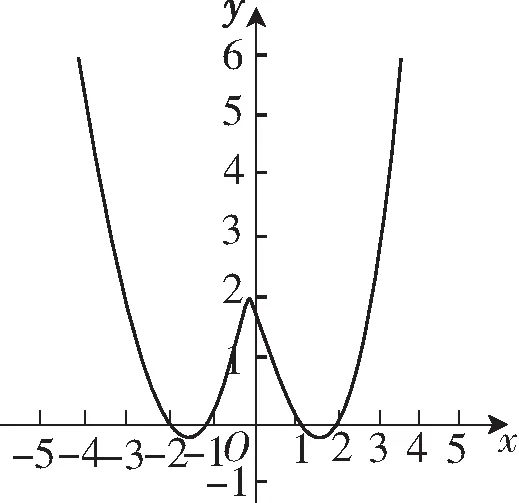
圖4
生:圖像都是有升也有降.
師:還有嗎?
生:都是在某一段上上升或下降.
師:非常好!嚴謹的說,在某個區間上函數圖像保持上升或下降.
師:從圖3和圖4的共同特點,我們不難發現函數的單調性是一個局部的概念,即“在某個區間上函數圖像保持上升或下降”.
設計意圖:學生在初中學習過函數的單調性,采用描述“y隨著x的增大而增大(減小)”這就是我們從函數圖像上看到的函數的變化趨勢,即變化中的不變性,所以學生借助于初中的經驗還是能夠說出這種規律的教學.
教學片段1和2,使學生感受研究函數性質的必要性,結合初中所學,從而做到數學抽象的抽象的具體化生成了抽象的定性化.
1.2 抽象的定性化促進了抽象的定量化
從函數圖像觀察到的函數單調性是“定性”的,需要進一步進行“定量化”,即用“定量”的方法對這一性質準確刻畫.
教學片段3具體實例 定量分析
問題7 我們以f(x)=x2為例,你能從函數的對應關系出發說出圖5中點A的兩個坐標的意義嗎?
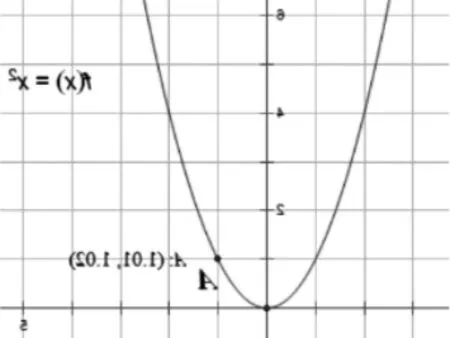
圖5
生:1.02為自變量取1.01時的函數值.
問題8 我們以f(x)=x2為例,你是理解“y隨著x的增大而增大(減小)”的?你能說說它的數量特征是什么嗎?
通過幾何畫板(如圖6),在y軸右側的沿x增大的方向拖動點A,讓學生觀察點A的坐標變化,引導他們得出函數值的變化規律:函數值隨自變量的增大而增大.
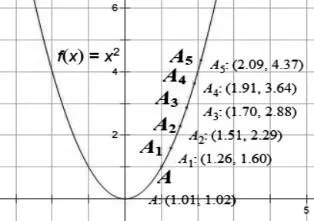
圖6
設計意圖:上述程序實現將函數f(x)=x2在區間(0,+∞)上“圖像上升”這一不變性轉化為“函數值隨自變量的增大而增大”的數量描述.盡管仍是“定性刻畫”,但是它離用精確的數量關系進行“定量刻畫”已經近一步了.
問題9:“x增大了”怎么用符號語言表示?“對應的函數值y增大”又該如何表示呢?我們以f(x)=x2為例,認真填寫表格,你給出具體定量描述嗎?

…123456…f(x)=x2……
生:當x從1增大到2時,則f(x)從1增大到4,當x從2增大到3時,則f(x)從4增大到9,當x從3增大到4時,則f(x)從9增大到16,當x從4增大到5時,則f(x)從16增大到25,當x從5增大到6時,則f(x)從25增大到36.
問題10 這種函數值隨自變量的增大而增大的變化過程能寫的完嗎?
生:不能,因為在區間(0,+∞)中自變量為實數,有無數個.
問題11 你能借助當從5增大到6,歸納出上述具體例子的共同特點嗎?
師:當x從1增大到2時,則f(x)=x2從1增大4,我們用不等式如何描述?
生:當1<2時,f(1) 師:以此類推,當x從2增大到3,當x從3增大到4,當x從4增大到5,當x從5增大到6,我們可以得到f(2) 生:只要x1 設計意圖:當把函數f(x)在區間(0,+∞)上的單調性聚焦在“函數值隨自變量的增大而增大”后,學生對“定量刻畫”函數性質的必要性與數學意義該有所體驗.但如何用數量關系精確刻畫這種定量關系,對學生來說還是很抽象的,因此設計時由具體到一般,讓學生逐步生成這種定量關系. 教學片段4精準定量 生成符號 問題12 當x1 生:如圖7,我們知道不可以取某些特殊數. 圖7 問題13 你覺得更嚴格的表達應該是怎樣的? 學生小組討論 生:任取x1,x2. 師:你能精確的描述這種不等關系嗎? 生:任取x1,x2∈(0,+∞),當x1 師生共同歸納:在定義域D的某個區間I上任意取的兩個數x1,x2,當x1 設計意圖:這個環節是本節課的重點、難點,其核心是通過具體到抽象的過程,讓學生學會用嚴格的語言符號刻畫函數的單調性,通過問題串,設法讓學生體會“任意”,引導他們符號語言表達,從而初步做到抽象的定量化到抽象的符號化. 教學片段5類比探究 抽象定義 問題14 類比增函數的探究方法,探究函數在區間上隨著的增大而減小? 問題15 我們應該如何類比探究呢? 生:只需要在函數圖像上任取兩個點比較它們自變量和函數值的大小即可. 師:下面請大家通過幾何畫板上在函數圖像上任取兩個點比較它們自變量和函數值的大小它們有何關系? 探究完成后老師引導學生完成下列問題: (1)學生用符號語言描述y隨x的增大而減小:________________. (2)學生類比增函數定義得出減函數的定義:________________. 師生共同歸納:在定義域D的某個區間I上任意取的兩個數x1,x2,當x1 設計意圖:設計讓學生體會“類比”方法的作用,問題15幫助學生找到類比探究方向,同時通過學生在電腦上用幾何畫板探究,再次體會“任意……都……”的含義,進而歸納抽象出減函數的定義. 教學片段6概念辨析 鞏固新知 辨析1:若定義在區間[-2,3]的函數f(x)滿足f(-2) 辨析2:函數在區間(1,3) 和[3,5]都是增函數,則函數在區間 (1,5]上一定也是增函數嗎? 設計意圖:通過三個辨析讓學生再次體會“任意……都……”的含義,加深學生對定義的理解,通過辨析2、3體會正因為單調性強調“任意……都……”從而導致了單調性是函數的局部性質這一特征,通過辨析3讓學生對初中三大函數單調性有了完整的認識. 搞好概念教學是實現數學抽象的落腳點[2],數學概念是數學知識的基礎,是數學思維的基本形式.因此,概念課教學中不能忽略概念,把概念課上成習題課,要注重概念的生成,在概念形成的學習中讓學生學會數學抽象.那么,概念的生成體現在哪些方面呢?我們需要關注哪些? 2.1客觀原型是引入抽象概念的出發點 對于數學概念來說,它最基本的原型就是生活經驗.因此,數學核心素養的提出,目的在于強調數學源自生活而又應用于生活.基于核心素養,教材的對抽象抽象概念的編寫也是以“生活情境——建立模型——解釋應用”.如概率統計中的正態分布密度函數是由大數學家高斯根據生活中大量的數據抽象出來的數學模型,正態分布密度函數是一個很好的適用于現實生活中許多事物和現象的概率法則,又比如牛頓依據蘋果落地這樣一生活事實抽象出萬有引力定律數學模型.因此,可以這樣說,生活經驗是數學抽象發展的重要載體. 該設計以形象的函數圖像為出發點引出“函數單調性”這一抽象數學概念,而函數單調性的概念是則由于舍棄了其他成分而僅僅著眼于量的關系的分析獲得了更為普遍的意義,因此函數單調性的概念是這些眾多生活經驗的共性的提煉.可以說,數學抽象的關鍵是從眾多生活經驗的諸多性質中提煉出其本質屬性. 2.2邏輯發展是滲透數學抽象的著力點 數學抽象概念的發展是具有層次性的,它是由低向高逐步發展的.因此,在教授數學抽象概念時,應該重視新舊數學抽象概念之間的邏輯相關性[3].使原認知結構中的有關知識與新學習的內容相互作用,經過 同化和順應,逐步完善和發展學生的數學認知結構. 由初中階段的用“隨著的增大而增大(減小)”來刻畫函數圖像從左到右的上升(下降)到高中的精確的定量關系,把這表面上看起來似乎不是特別有關系的抽象概念有機結合起來,通過邏輯發展,建立起薪的理論結構. 2.3符號語言是描述抽象概念的核心點 當今的數學世界是一個優美壯觀的符號世界,數學符號是在數學抽象化的基礎之上由數學家們在研 究工作中逐步引入的,并且以此為基礎把數學對象的研究轉化為數學符號的研究[3].在函數單調性的概念教學中,通過邏輯發展,學生能夠理解“隨著的增大而增大(減小)”來刻畫函數圖像從左到右,但是用自然語言的表述函數單調性的概念顯然使學生思維不夠清晰和流暢,此時,如果堅持用自然語言來表述的話,勢必導致學生思維上的紊亂,因此,在數學抽象概念教學中,數學符號的引入就顯得尤為重要了. 但是數學符號有層次、有結構、有系統,其中基本符號是用以表示簡單的抽象概念,由若干基本符號而構成的組臺符號,可以之表示較復雜的抽象概念,通過類比思想,我實現從數學的形式化推動了數學的符號化,至此我們完整的經歷抽象到科學抽象再到數學抽象三個過程,學生在知識形成過程中逐步體會和理解知識,并能應用數學語言表達,進而逐步形成抽象思維能力.學生體會從量變到質變的辯證思想,實現概念的飛躍. 總之,數學抽象是一個量變到質變的過程,在教學中我們要學生經歷具體化到抽象化在到符號化的生成過程,真正的讓核心素養落到實處.1.3 抽象的定量化推動了抽象的符號化
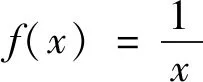
2.數學抽象的教學反思

