山色水聲裹游行

段志貴 鄒翔如 陳喆

【摘? ?要】小學階段是學生數(shù)學思維發(fā)展的重要階段。以一道龜兔賽跑題為例，通過對題目由表象到本質的層層剝離，啟發(fā)和引領小學生逐步深化對數(shù)學問題解決的認識和理解，發(fā)展解題思維，努力實現(xiàn)解題境界由低級到高級的四重體驗。

【關鍵詞】問題解決; 數(shù)學思維;小學數(shù)學

小學階段是提高學生數(shù)學學習興趣、激發(fā)學生學習內驅力、發(fā)展學生數(shù)學思維的一個極其重要的階段。根據(jù)皮亞杰認知發(fā)展階段理論，小學生的認知正處于從前運算階段到形式運算階段的過渡階段，思維正處于從形象思維走向抽象思維的過渡時期。解決問題是發(fā)展數(shù)學思維的重要途徑。通過問題解決發(fā)展小學生的數(shù)學思維，教師既要著力引導學生從具象逐步走向抽象，也要注意為學生提供具體實物的支撐。以一道思維含量較高的龜兔賽跑題為例，分析小學生解題思維由低級到高級的四重體驗。

一、逢山遇水：淺讀題目，探尋問題

題目：龜兔進行10000米賽跑，兔子的速度是烏龜速度的5倍。它們同時從起點出發(fā)，烏龜不停地奔跑，兔子跑到某一地點開始睡覺。兔子醒來時，烏龜已經(jīng)領先兔子5000米。兔子奮起直追，但烏龜?shù)竭_終點時，兔子仍落后100米。試求兔子睡覺期間烏龜跑了多少米？1

這是一個表述很復雜的問題，剛接觸題目時，小學生受自身思維發(fā)展階段的局限，面對冗長的題目，常常不知道如何合理運用條件，尋找突破口。這正是學生解題經(jīng)歷的第一階段，在這一階段中，他們往往止步于對題意的表象理解，很難真正讀懂題目。也就是他們常常表現(xiàn)出能讀懂“故事”，卻讀不懂故事中蘊含的數(shù)量關系。雖然題目中的數(shù)據(jù)都已明確出現(xiàn)，但此時他們卻不知道所給出數(shù)據(jù)的意義何在，以及該如何運用。

這是學生解題過程中的第一境界——入一座山，見一方水，尚處于解題的迷茫階段。

二、觀山看水：圖形表征，分析問題

隨著對問題理解的深入，小學生可能會把思維的觸角延伸到問題條件的轉換上。有的學生可能會嘗試著通過觀察具象的路程示意圖去理解和轉換問題。這依舊是一種具象思維的水平，此時學生對于數(shù)學題中的數(shù)量關系，并不能很好地運用抽象思維去思考。這時教師要引導學生重新分析題意，先用具體的數(shù)體現(xiàn)龜兔速度之間的關系，即如果烏龜?shù)乃俣葹?，那么兔子的速度就是5，然后借助具象的圖式來輔助解決問題，以此來彌補他們思維發(fā)展的局限性。

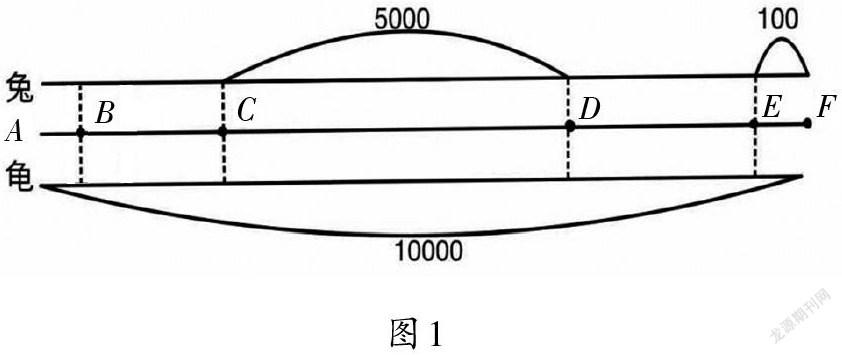
借助線段圖（如圖1）將“故事”再講一遍，龜兔進行10000米賽跑，即AF=10000米，烏龜?shù)乃俣仁?，兔子的速度是5。它們從A點一起出發(fā)，兔子跑到C點時烏龜?shù)竭_B點，兔子醒來時依然在C點，這時烏龜已到達D點，即CD=5000米，烏龜?shù)竭_終點F時兔子到達E點，即EF=100米，求兔子睡覺期間烏龜跑了多少米，也就是求BD之間的距離是多少。

這是學生解題經(jīng)歷的第二個階段。在這一階段中，學生能夠借助圖式等輔助手段，將問題初步“數(shù)學化”，逐步厘清題目中的條件、問題以及相應的數(shù)量關系。這時學生已經(jīng)能夠“見山是山，見水是水”了。

三、跋山涉水：立足發(fā)現(xiàn)，解決問題

厘清問題后，學生開始嘗試進入問題解決的階段。

根據(jù)對圖1的分析，兔子從C點開始以速度5追趕烏龜，此時烏龜在D點以速度1向終點F行進，當烏龜?shù)竭_終點F時，兔子到達E點，距離終點F還有100米。在兔子追趕烏龜?shù)倪^程中，烏龜走了路程DF（即DE+EF），兔子走了路程CE（即CD+DE）。

同一時間是解題的一個抓手。據(jù)此，可首先求出在后面這一相同時間里兔子比烏龜多走的路程。此時兔子比烏龜多走了CE-DF=CD+DE-（DE+EF）=5000-100=4900（米）。

（1）兔子睡覺前（龜兔同時出發(fā)直至兔子睡覺）這段時間里烏龜行進的路程為：ΑΒ=755×1=755（米）。

（2）兔子睡醒后（兔子追趕烏龜直至烏龜?shù)竭_終點）這段時間里烏龜行進的路程為：DF=1225×1=1225（米）。

所以，兔子睡覺時烏龜行進的路程為：BD=AF-AB-DF=10000-755-1225=8020（米）。

把上述思維梳理一下，實質上就是后面兔子在追趕烏龜?shù)倪^程中多走了CE-DF=（CD+DE）-（DE+EF）=CD-EF=5000-100=4900（米）。

這時兔子比烏龜多走了BC=3775÷5×5-1=3020（米），所以在兔子睡覺期間，烏龜走了BD=BC+CD=3020+5000=8020（米）。

在這一解法中，借助于直觀的線段圖，學生破譯了題目給出的復雜的數(shù)量關系，題目所給的條件都被充分利用，學生感受到題目中的每一個條件都是必須的且重要的。這一解題思維不僅具有形象性，也暗藏著一定的抽象性與邏輯性，顯然突破了前兩個階段的層級，給了學生“見山不是山，見水不是水”的解題新體驗，即學會變換已知條件，認準解題方向，逐步接近解題目標。

四、顯山露水：拓展理解，透視問題

有了前面三重體驗，接下來學生迫切想進入第四重體驗，這就是深入理解題意，分析各類條件量與量之間的關系，試圖從不同角度去理解問題，抓住問題本質，從而捕捉著力點，尋找突破口。

首先，我們看到烏龜跑的路程可分為兩個部分，一是兔子跑時烏龜跑的路程，二是兔子睡覺時烏龜跑的路程。在第一部分中，龜兔都跑，按照它們速度的5倍關系，兔子跑9900米，烏龜應跑9900÷5=1980（米）;第二部分為待求路程，即兔子睡覺時烏龜所走的路程。這兩部分之和實際上是烏龜跑完的總路程——10000米，所以10000米與1980米的差8020米就是兔子睡覺時烏龜跑的路程了。

我們也可以這樣想：如果兔子先不睡覺，一直跑到距離終點還有100米時再睡覺，那么兔子就是跑了10000-100=9900（米）。兔子跑9900米的同時，烏龜跑了9900÷5=1980（米）。當兔子醒來時，烏龜已經(jīng)跑完了10000米，所以烏龜在兔子睡覺時行進了10000-1980=8020（米）。2

這里將兔子睡覺的過程直接移到最后，避免了因為多了兔子睡覺這一環(huán)節(jié)使得整個行進過程被分得四分五裂而造成小學生思維混亂的情況。這樣一來題目被簡化，不用考慮得很復雜，減少了錯誤產(chǎn)生的可能性并進一步揭露了問題的本質。

同樣的思維模式，我們從另一個角度來思考：依然假設兔子不睡覺，那么在烏龜完成了10000米行程的同時，兔子應該走了10000×5=50000（米）。但實際上兔子只走了10000-100=9900（米），所以兔子因為睡覺少走了50000-9900=40100（米）。因此當兔子睡覺時停止行進，烏龜卻在繼續(xù)向前，又因為龜速是兔速的15，所以烏龜在兔子睡覺時行走了40100÷5=8020（米）。

這正是題目待求的里程。以上兩種解法均屬于同一種解題思路，均將多余條件“兔子醒來時，烏龜已經(jīng)領先兔子5000米” 拋棄，解法更加簡潔、巧妙。兩步運算，題目迎刃而解！

此外，我們還可以這樣理解題意。由題可知，兔子醒來后跑了CE，在此期間，烏龜跑的路程是DF，且兔子的速度是烏龜?shù)?倍，那么我們就可以得到一個關系式CE=5DF，于是可以分成CD+DE=5DE+5EF。

不妨設DE=x，則關系式又可以寫成5000+x=5x+500，DE=1125（米），那么AC=AF-CD-DE-EF=10000-5000-1125-100=3775（米）。此時，烏龜在兔子走到C點時，已經(jīng)走的路程為：AB=AC÷5=3775÷5=755（米），則烏龜在兔子睡覺時一共走了BD=BC+CD=3775-755+5000=8020（米）。

這種解法的核心采用了解方程的方法。用方程來表示我們在題目中挖掘出來的關系式，利用已知條件，代入方程就很容易求出所需要的DE的距離，那么待求的路程也就迎刃而解了。

最后，我們還可以對題目進行改編：龜兔賽跑，同時同地出發(fā)，全程10000米，龜速30米/分，兔速330米/分，跑了10分鐘，兔子停下來睡覺4小時，醒來時發(fā)現(xiàn)烏龜已經(jīng)超過，于是立即追趕，問能否在烏龜?shù)竭_終點前追上？如果能追上，問此時離終點還有多遠？

在這一改編中，烏龜跑了30×250=7500（米），和兔子的距離為7500-330×10=4200（米）。兔子追趕的時間為4200÷330-30=14（分鐘），離終點10000-7500-30×14=2080（米）。

上述幾種巧妙解法以及對問題的深化理解，借助于題目的語言描述，圍繞數(shù)量關系展開思考，能夠透過題目所給條件，分析問題本質，抓住解題關鍵，從直觀具體過渡到聯(lián)想抽象，顯然這已是解題的最高境界——“見山還是山，見水還是水”，即透過給定條件，分析和梳理內在關系，尋找解題制高點。

數(shù)學問題的解決，理解題意是前提，抓住問題的本質是關鍵，發(fā)展學生從直觀具體到聯(lián)想抽象的數(shù)學思維，是解題教學的終極目標。本題的教學基于小學生的認知規(guī)律及潛能外化規(guī)則，逐步躍進思維層次，使得問題的解決持續(xù)走向深入。在從低到高的每一次解題思維躍進中，可以深刻地感受到數(shù)學解題四重體驗的不斷遞進，學生的解題水平不斷提升，學習興趣不斷增強，創(chuàng)造性思維能力不斷發(fā)展。

參考文獻：

1謝玉華.一道競賽題的第四種解法J.小學教學研究，1999（3）：27.

2李會生，劉雪艷.只在深水中航行：把枝節(jié)問題撂一邊J.小學教學參考，2007（7/8）：74.

（1.鹽城師范學院數(shù)學與統(tǒng)計學院? ?224002 2.青海師范大學數(shù)學與統(tǒng)計學院? ?810008）