梯形槽聚乙烯緩沖襯墊結(jié)構(gòu)的有限元優(yōu)化設(shè)計(jì)

李國(guó)志，段毛毛，羅之遙，孫德強(qiáng)

緩沖與隔振

梯形槽聚乙烯緩沖襯墊結(jié)構(gòu)的有限元優(yōu)化設(shè)計(jì)

李國(guó)志1,2,3，段毛毛1,2,3，羅之遙1,2,3，孫德強(qiáng)1,2,3

（1.陜西科技大學(xué)，西安 710021；2.中國(guó)輕工業(yè)功能印刷與運(yùn)輸包裝重點(diǎn)實(shí)驗(yàn)室，西安 710021； 3.輕化工程國(guó)家級(jí)實(shí)驗(yàn)教學(xué)示范中心，西安 710021）

探究梯形槽EPE緩沖襯墊結(jié)構(gòu)的動(dòng)態(tài)緩沖性能，優(yōu)化緩沖襯墊結(jié)構(gòu)，為后續(xù)緩沖結(jié)構(gòu)設(shè)計(jì)提供科學(xué)的參考方案。以密度為23 kg/m3的EPE材料為試驗(yàn)對(duì)象，對(duì)材料樣品進(jìn)行靜態(tài)壓縮試驗(yàn)，數(shù)據(jù)處理得出應(yīng)力-應(yīng)變數(shù)據(jù)，將其導(dǎo)入Ansys Workbench材料庫(kù)中，對(duì)產(chǎn)品襯墊系統(tǒng)進(jìn)行有限元沖擊模擬。將沖擊理論計(jì)算結(jié)果與有限元分析結(jié)果進(jìn)行對(duì)比。保持等效接觸面積不變，對(duì)不同底角度數(shù)和開槽排布方式的產(chǎn)品襯墊系統(tǒng)進(jìn)行有限元模擬，得出最大變形量、等效應(yīng)力、速度等數(shù)據(jù)。底角小于70°時(shí)，緩沖結(jié)構(gòu)整體剛度過小，導(dǎo)致跌落時(shí)產(chǎn)品觸底，不能很好地保護(hù)產(chǎn)品；當(dāng)?shù)捉谴笥?0°時(shí)，度數(shù)為85°的緩沖襯墊等效應(yīng)力最小，為0.0966 MPa，并且產(chǎn)品的速度改變量最小。底角為90°時(shí)，1個(gè)槽緩沖襯墊變形量最大，為30.282 mm，等效應(yīng)力為0.09681 MPa。在結(jié)構(gòu)設(shè)計(jì)時(shí)，可將底角85°、1個(gè)槽的緩沖結(jié)構(gòu)作為設(shè)計(jì)的最佳參考值，以實(shí)現(xiàn)緩沖材料的減量化設(shè)計(jì)和最佳的保護(hù)性能的目標(biāo)。

發(fā)泡聚乙烯；緩沖包裝；梯形；動(dòng)態(tài)緩沖性能

緩沖包裝設(shè)計(jì)要求緩沖材料能夠有效地吸收流通過程中傳向產(chǎn)品的外力，能充分吸收和分散外力產(chǎn)生的能量，防止產(chǎn)品損壞。設(shè)計(jì)時(shí)應(yīng)使用經(jīng)濟(jì)、符合環(huán)保要求的緩沖包裝材料，并以最小的資源達(dá)到最大的保護(hù)效果，節(jié)省包裝成本。在緩沖包裝材料方面，有學(xué)者從影響緩沖材料性能的因素著手研究，以便為緩沖結(jié)構(gòu)設(shè)計(jì)提供依據(jù)[1—5]。在材料緩沖性能的研究方法上，多集中于試驗(yàn)方法和有限元模擬[6—10]。針對(duì)緩沖襯墊結(jié)構(gòu)方面的研究，李志強(qiáng)等[11]借助靜態(tài)壓縮試驗(yàn)，以發(fā)泡聚苯乙烯（EPS）為材料，通過改變正棱臺(tái)緩沖襯墊的厚度及斜面傾角，研究不同結(jié)構(gòu)參數(shù)的正棱臺(tái)緩沖墊靜態(tài)緩沖性能的差異。李淑娟等[12]以發(fā)泡聚乙烯（EPE）為材料，對(duì)側(cè)面傾角不同的正棱臺(tái)異型緩沖墊進(jìn)行靜態(tài)壓縮試驗(yàn)，研究異型緩沖墊的靜態(tài)緩沖性能，并探究其與普通緩沖墊的性能差異，結(jié)論為緩沖包裝設(shè)計(jì)提供理論支持。李國(guó)志等[13]應(yīng)用仿真和試驗(yàn)相結(jié)合的方法，研究隨機(jī)振動(dòng)時(shí)不同密度EPE、垂直方向不同振動(dòng)間隙時(shí)，緩沖襯墊的隔振性能，這在實(shí)際包裝設(shè)計(jì)過程有重要的意義。馮紅蜻等[14]利用仿真分析與試驗(yàn)測(cè)試結(jié)合的方法，研究EPE在相同受壓面積、不同表面積、受壓厚度和復(fù)合圍框結(jié)構(gòu)的情況下，EPE靜態(tài)緩沖性能的變化，目的是解決EPE包裝設(shè)計(jì)的工程問題。

上述研究還不足以完全解決實(shí)際包裝設(shè)計(jì)環(huán)節(jié)的問題，實(shí)際包裝結(jié)構(gòu)設(shè)計(jì)主要依賴設(shè)計(jì)師的經(jīng)驗(yàn)，以及參考其他類似結(jié)構(gòu)布局來設(shè)定初始結(jié)構(gòu)。初始結(jié)構(gòu)對(duì)優(yōu)化設(shè)計(jì)時(shí)緩沖性能影響較大，但在確定初始結(jié)構(gòu)時(shí)，缺乏理性系統(tǒng)的設(shè)計(jì)方法，前人在這方面的研究也相對(duì)較少，因此，文中將探究EPE緩沖襯墊構(gòu)型對(duì)其動(dòng)態(tài)緩沖性能的影響，為泡沫材料作為緩沖包裝時(shí)的結(jié)構(gòu)設(shè)計(jì)提供指導(dǎo)，以實(shí)現(xiàn)緩沖包裝的優(yōu)化設(shè)計(jì)。

1 跌落沖擊計(jì)算模型

1.1 緩沖材料力學(xué)性能試驗(yàn)

緩沖材料為23 kg/m3的層壓發(fā)泡聚乙烯（Laminated EPE），樣品尺寸100 mm100 mm50 mm，采用GB/T 8168—2008《包裝用緩沖靜態(tài)壓縮試驗(yàn)方法》[15]中A方法對(duì)試樣做靜態(tài)壓縮試驗(yàn)，得到該材料的壓力-變形曲線，然后將數(shù)據(jù)進(jìn)行處理并分析，繪制出材料的應(yīng)力-應(yīng)變曲線（-），見圖1。

1.2 有限元模型

在包裝件跌落沖擊過程中，不考慮易損件，將產(chǎn)品襯墊系統(tǒng)作為包裝件的近似模型，對(duì)其進(jìn)行有限元面跌落分析。文中建立了產(chǎn)品襯墊系統(tǒng)的有限元模型，見圖2。模型由產(chǎn)品、緩沖襯墊、地面等3部分構(gòu)成。

在跌落過程中，其材料參數(shù)設(shè)置對(duì)分析結(jié)果有很大影響。經(jīng)過對(duì)應(yīng)力-應(yīng)變曲線分析及查閱資料[13]得到材料參數(shù)見表1。

簡(jiǎn)化后的模型采用自由網(wǎng)格劃分即可。對(duì)模型進(jìn)行接觸設(shè)置，將產(chǎn)品（5.4 kg）與緩沖襯墊接觸部位設(shè)置為摩擦接觸，動(dòng)靜摩擦因數(shù)均設(shè)置為0.2；襯墊與地面之間設(shè)置為無摩擦接觸。根據(jù)國(guó)家標(biāo)準(zhǔn)規(guī)定的跌落試驗(yàn)的試驗(yàn)高度[16]，確定跌落高度為800 mm。為了減少仿真計(jì)算時(shí)間，剛性地面與EPE結(jié)構(gòu)之間的距離設(shè)置為2 mm，其余高度轉(zhuǎn)化為模型跌落時(shí)的初始速度為方向?3956 mm/s；對(duì)所有模型設(shè)置重力加速度，為方向?9806.6 mm/s2；跌落地面設(shè)置固定約束。為確保產(chǎn)品在跌落后進(jìn)入反彈階段，將計(jì)算時(shí)間設(shè)置為25 ms。

考慮緩沖襯墊結(jié)構(gòu)的穩(wěn)定性，改變襯墊模型的開槽個(gè)數(shù)及底角度數(shù)，產(chǎn)品襯墊系統(tǒng)模型見圖3。將梯形槽個(gè)數(shù)設(shè)計(jì)為1～3個(gè)，包含平行槽和交叉槽（后文涉及的“x”表示交叉形式）結(jié)構(gòu)，梯形槽高度50 mm，底角為90°，共5種結(jié)構(gòu)（見圖4）。底角角度設(shè)計(jì)為55°～90°，間隔為5°，梯形槽結(jié)構(gòu)為2個(gè)平行槽，高度為50 mm，共8種結(jié)構(gòu)。底部緩沖襯墊與側(cè)面緩沖襯墊為粘合一體結(jié)構(gòu)，共建立13種模型，模型參數(shù)見表2。

1.3 包裝件跌落沖擊過程

研究不同構(gòu)型緩沖襯墊的緩沖性能，在此過程中以產(chǎn)品對(duì)跌落沖擊的響應(yīng)來分析襯墊的緩沖性能，即產(chǎn)品的位移、速度、加速度在沖擊過程中隨時(shí)間變化的規(guī)律。

表1 材料屬性

圖3 產(chǎn)品襯墊系統(tǒng)模型

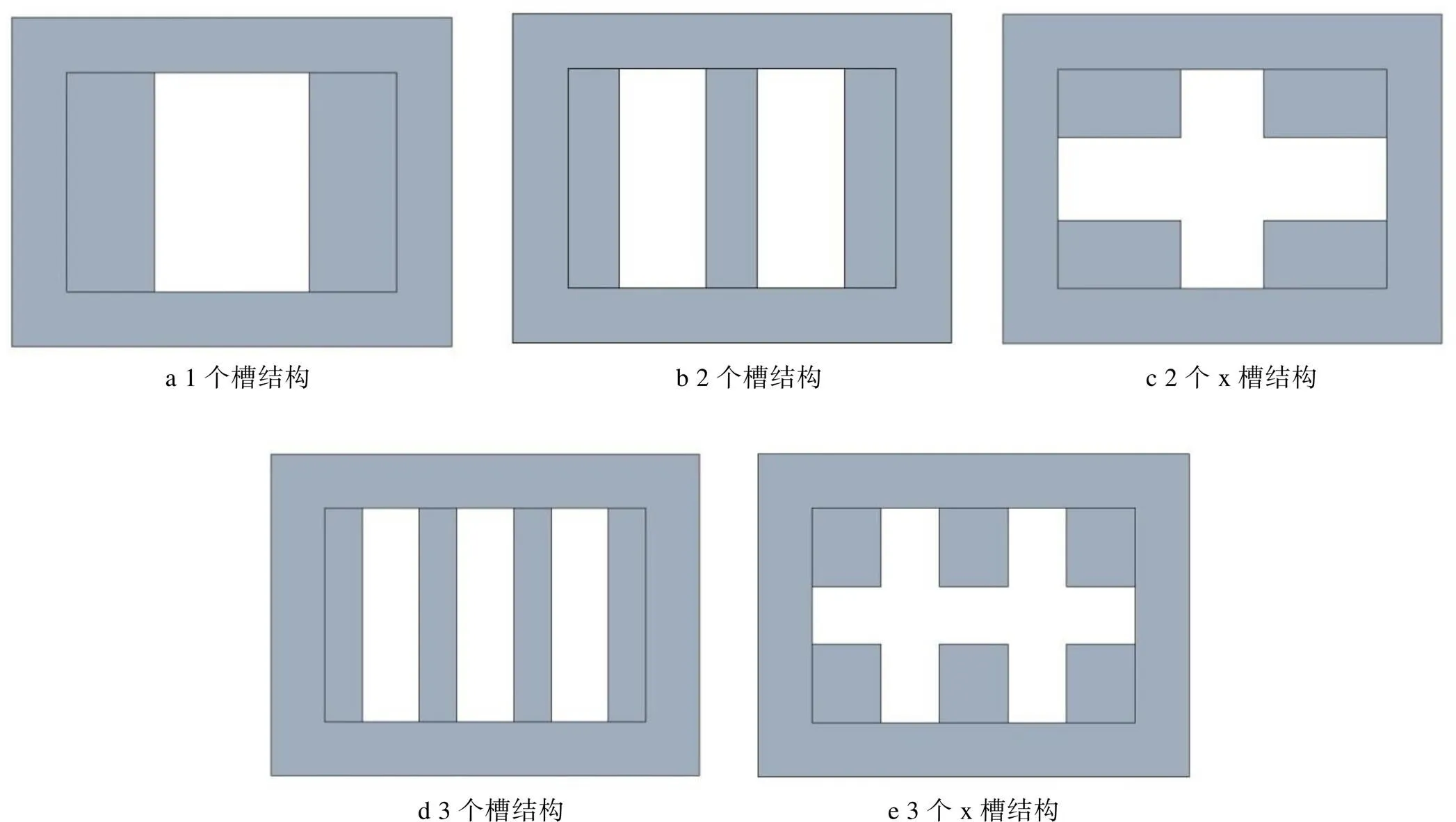
圖4 襯墊不同開槽數(shù)量的模型結(jié)構(gòu)

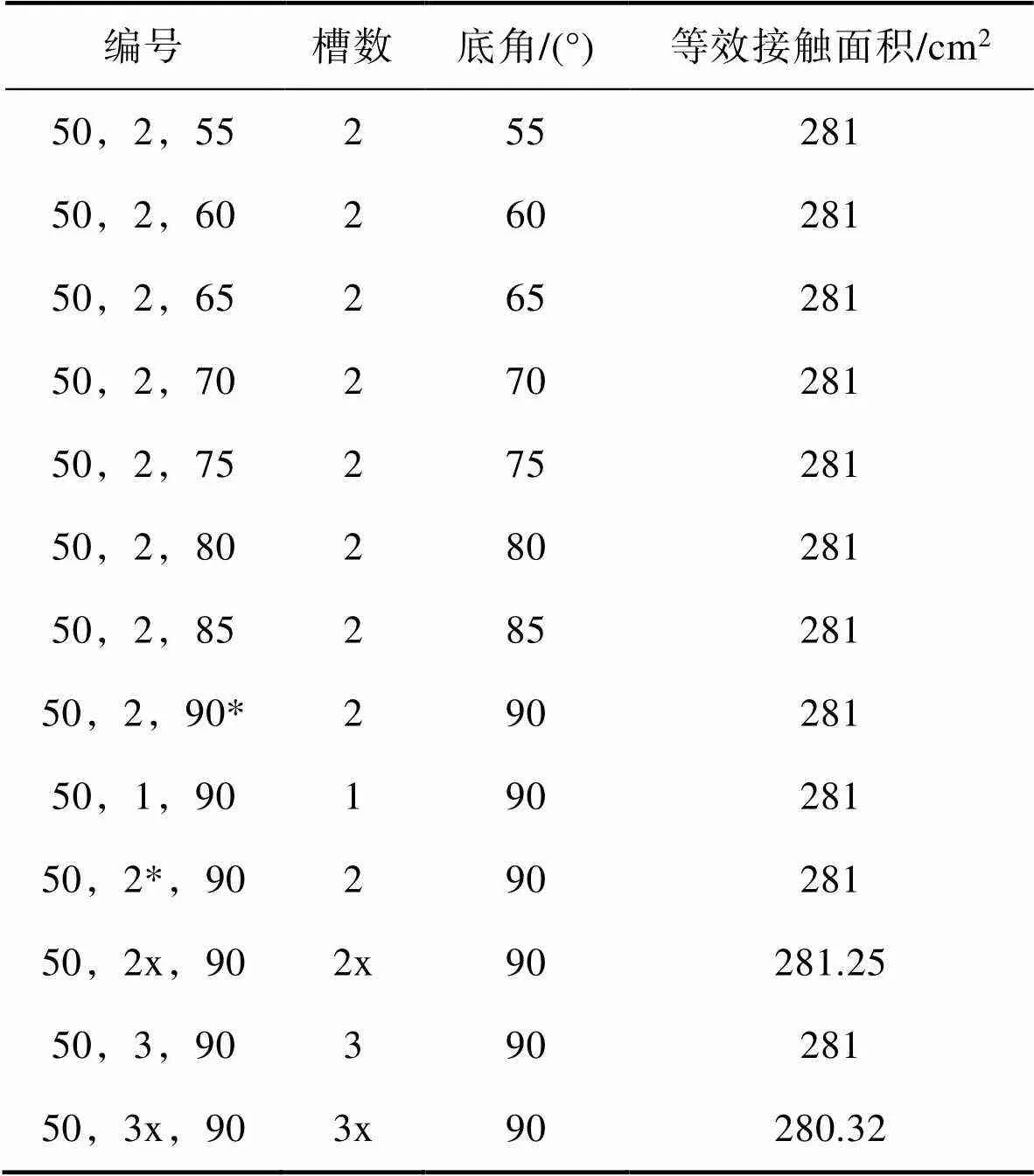
表2 緩沖襯墊構(gòu)型參數(shù)

注：編號(hào)為50，2，90*和50，2*，90的模型結(jié)構(gòu)相同，其中50，2，90*表示開槽方式不變，研究底角為90°時(shí)襯墊的緩沖性能；50，2*，90表示底角不變，研究底部為2個(gè)平行槽時(shí)襯墊的緩沖性能

設(shè)包裝件從高度處自由下落，不計(jì)阻力影響，包裝件接觸地面時(shí)的速度為：

(1)

負(fù)號(hào)表示為方向向下。包裝件接觸地面后緩沖襯墊停止運(yùn)動(dòng)，產(chǎn)品由于慣性作用繼續(xù)向下運(yùn)動(dòng)壓縮緩沖襯墊，同時(shí)產(chǎn)品在開始?jí)嚎s襯墊后速度逐漸減小，直到速度逐漸減小為0，緩沖襯墊吸收產(chǎn)品動(dòng)能使得壓縮量達(dá)到最大，此階段稱為變形階段。此后，襯墊彈性恢復(fù)力使產(chǎn)品向上運(yùn)動(dòng)，直到緩沖襯墊將其彈性能完全釋放，產(chǎn)品速度由零逐漸增大，此階段為恢復(fù)階段。彈性恢復(fù)后，包裝件在慣性作用下繼續(xù)向上運(yùn)動(dòng)，最后回彈高度為。產(chǎn)品跌落沖擊全過程[17]見圖5。

1.4 可靠性驗(yàn)證

湯伯森[17]等根據(jù)包裝件的力學(xué)模型研究產(chǎn)品對(duì)跌落沖擊的響應(yīng)，并得到產(chǎn)品在跌落沖擊過程中的位移-時(shí)間函數(shù)見式（2）。

(2)

(3)

(4)

(5)

產(chǎn)品落地時(shí)的速度為：

(6)

(7)

因此，產(chǎn)品在跌落沖擊過程中的速度改變量為：

(8)

為了驗(yàn)證有限元模型的可靠性，對(duì)底角90°，2個(gè)平行槽結(jié)構(gòu)的緩沖襯墊進(jìn)行了有限元仿真計(jì)算，結(jié)果見圖6。理論計(jì)算值與有限元模擬結(jié)果對(duì)比見表3，其中理論計(jì)算所得的產(chǎn)品跌落沖擊過程中持續(xù)時(shí)間、最大位移值、速度改變量、最大加速度值與有限元模擬結(jié)果的誤差分別為8.33%，8.18%，4.51%，11.94%，表明有限元模擬與理論計(jì)算的結(jié)果符合程度較好。

圖5 產(chǎn)品跌落沖擊全過程

Fig.5 Process of product falling impact

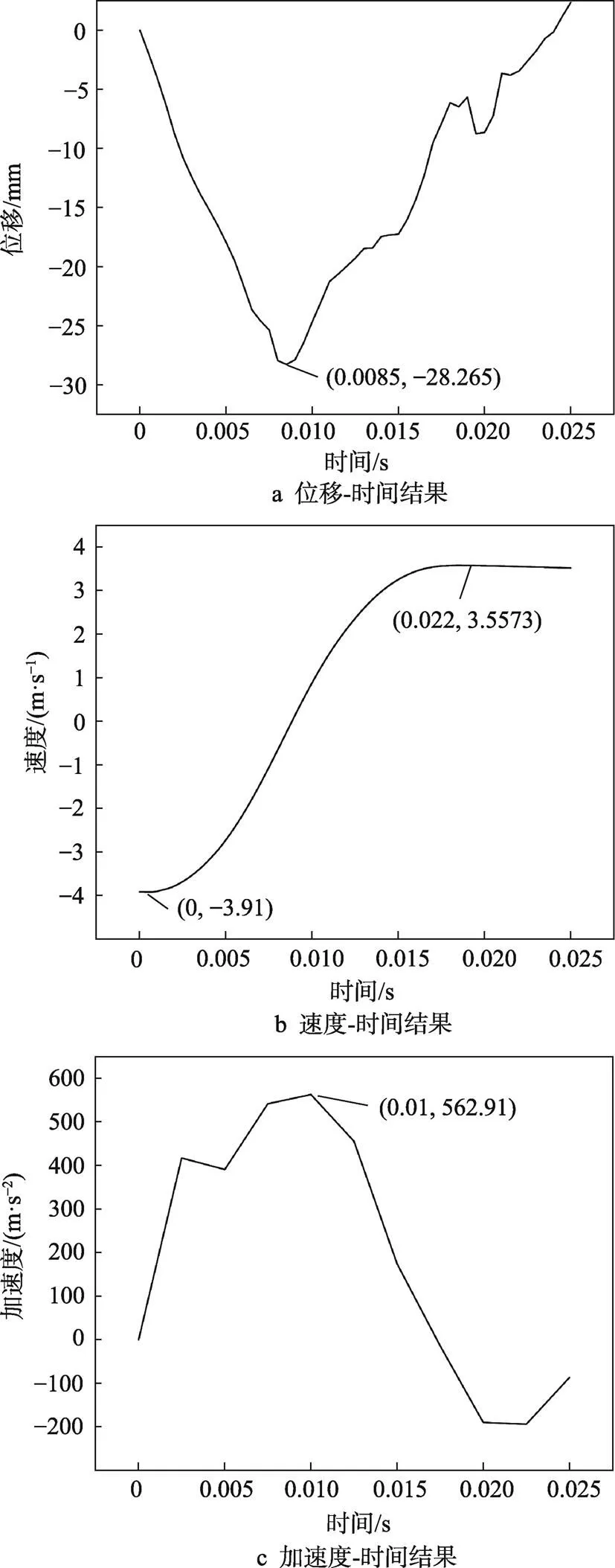
圖6 底角90°、2個(gè)平行槽結(jié)構(gòu)有限元計(jì)算結(jié)果

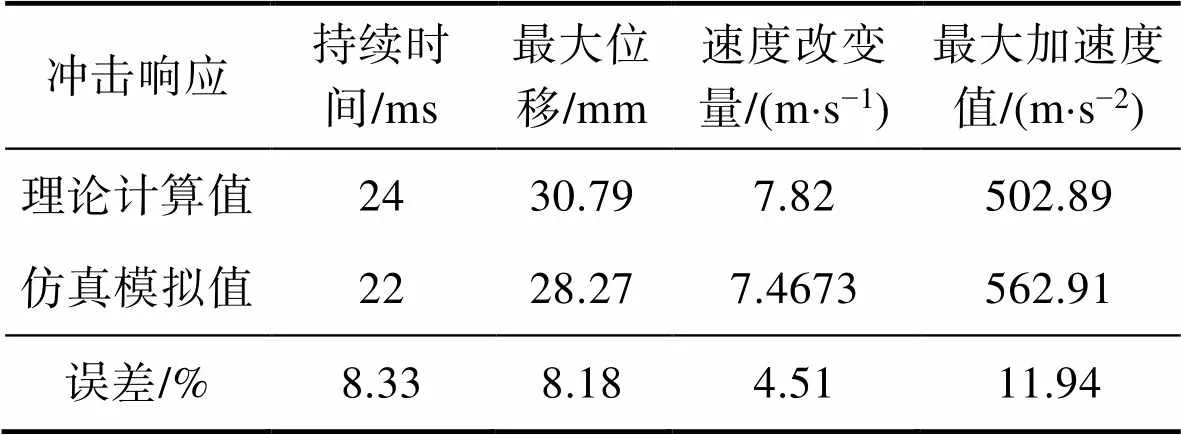
表3 模型理論計(jì)算與仿真模擬的誤差分析

2 結(jié)果與分析

2.1 底角對(duì)EPE緩沖性能的影響

2.1.1 最大變形量分析

產(chǎn)品沖擊到緩沖襯墊上直至襯墊被壓縮到變形極限，用緩沖襯墊的變形程度來描述其緩沖性能。襯墊厚度為50 mm、2個(gè)平行槽結(jié)構(gòu)、不同角度緩沖襯墊的最大變形量曲線見圖7。底角為55°～90°時(shí)的緩沖襯墊最大變形量分別為47.643，41.376，38.704，33.852，32.986，31.139，29.364，28.265 mm，變形量呈逐漸減小的趨勢(shì)，說明底角越大，緩沖泡沫結(jié)構(gòu)剛度越大，越不容易變形。底角小于70°時(shí)，變形量突然增大，原因是緩沖襯墊結(jié)構(gòu)剛度過小，可能存在結(jié)構(gòu)不穩(wěn)定現(xiàn)象，因此在結(jié)構(gòu)設(shè)計(jì)時(shí)，盡可能選擇底角大于70°的結(jié)構(gòu)，在70°～85°最佳。

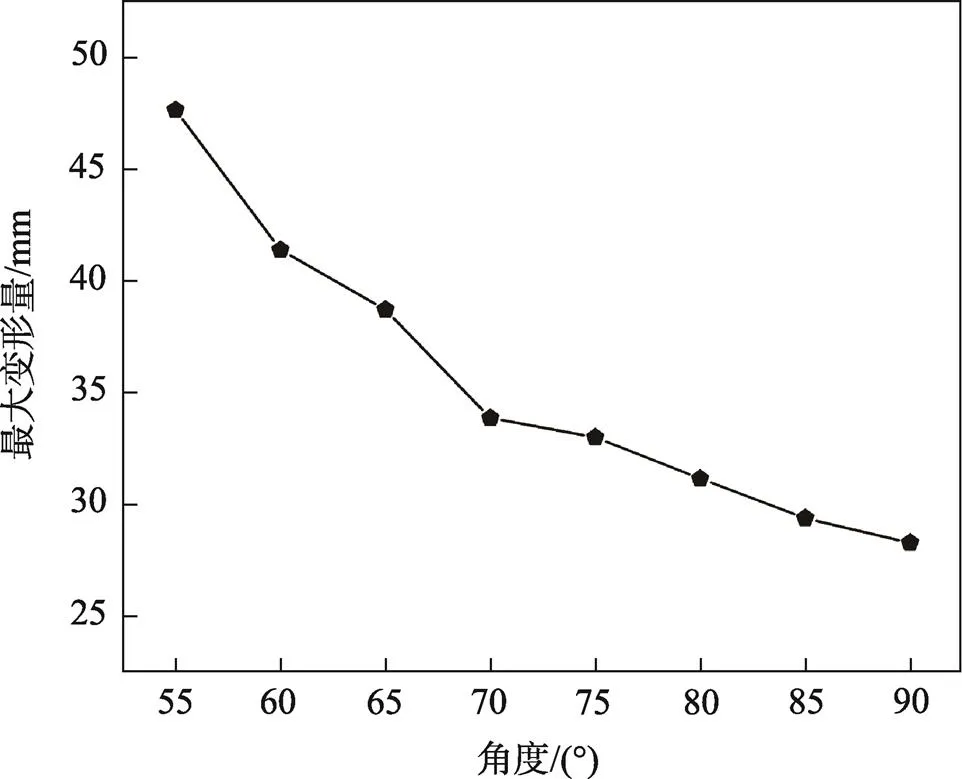
圖7 不同角度緩沖襯墊的最大變形量曲線

2.1.2 最大等效應(yīng)力分析

底角為55°～90°時(shí)的緩沖襯墊底部最大等效應(yīng)力值見圖8。底角在75°時(shí)，緩沖襯墊等效應(yīng)力為最大值。底角小于70°時(shí)的襯墊等效應(yīng)力會(huì)由于襯墊壓縮量過大而使中間高度的緩沖襯墊觸底，對(duì)產(chǎn)品有一定的損壞風(fēng)險(xiǎn)。底角大于70°時(shí)，底角為85°的緩沖襯墊等效應(yīng)力最小，為0.0966 MPa。

2.1.3 速度分析

產(chǎn)品在跌落過程中速度不斷增大，沖擊到襯墊表面時(shí)，襯墊的反作用力使得產(chǎn)品速度逐漸減小，當(dāng)速度變?yōu)?，緩沖襯墊被壓縮到極限。緩沖性能良好的泡沫結(jié)構(gòu)應(yīng)該盡可能延長(zhǎng)產(chǎn)品觸底所需要的時(shí)間。不同底角的襯墊緩沖時(shí)產(chǎn)品速度變化曲線見圖9。底角為55°～90°的緩沖襯墊被壓縮到極限時(shí)所經(jīng)歷的時(shí)間分別為0.0104，0.009 93，0.009 59，0.009 39，0.009 28，0.009 14，0.008 91，0.008 83 s。可以看出，隨著角度增加，沖擊所需的時(shí)間逐漸減小。產(chǎn)品完成一次沖擊后的速度大部分是按照逐漸增大的趨勢(shì)，說明緩沖襯墊釋放的彈性勢(shì)能對(duì)產(chǎn)品的沖擊逐漸增大。底角為55°時(shí)，產(chǎn)品經(jīng)過沖擊后的速度大于底角為60°，65°時(shí)產(chǎn)品的速度，這是由于緩沖襯墊底部梯形支撐部位與地面的接觸面積過小，這樣緩沖結(jié)構(gòu)整體剛度過小，材料變軟，導(dǎo)致跌落時(shí)產(chǎn)品觸底。角度為85°時(shí)，產(chǎn)品最終的速度小于角度大于70°時(shí)產(chǎn)品的速度，說明緩沖襯墊底角為85°時(shí)的緩沖性能是最優(yōu)的。

圖8 不同角度緩沖襯墊的等效應(yīng)力曲線

圖9 不同底角的襯墊緩沖時(shí)產(chǎn)品速度變化曲線

2.2 開槽分布對(duì)EPE緩沖性能的影響

2.2.1 最大變形量分析

厚度為50 mm，不同開槽分布的緩沖襯墊的最大變形量見表4。2個(gè)平行槽分布的緩沖襯墊變形量最小，為28.264 mm，3個(gè)平行槽結(jié)構(gòu)在沖擊時(shí)中間2塊泡沫出現(xiàn)瞬間失穩(wěn)現(xiàn)象，但是依然具有緩沖性能。1個(gè)槽時(shí)緩沖襯墊變形量最大，為30.282 mm，2種交叉開槽結(jié)構(gòu)最大變形量小于1個(gè)槽結(jié)構(gòu)。

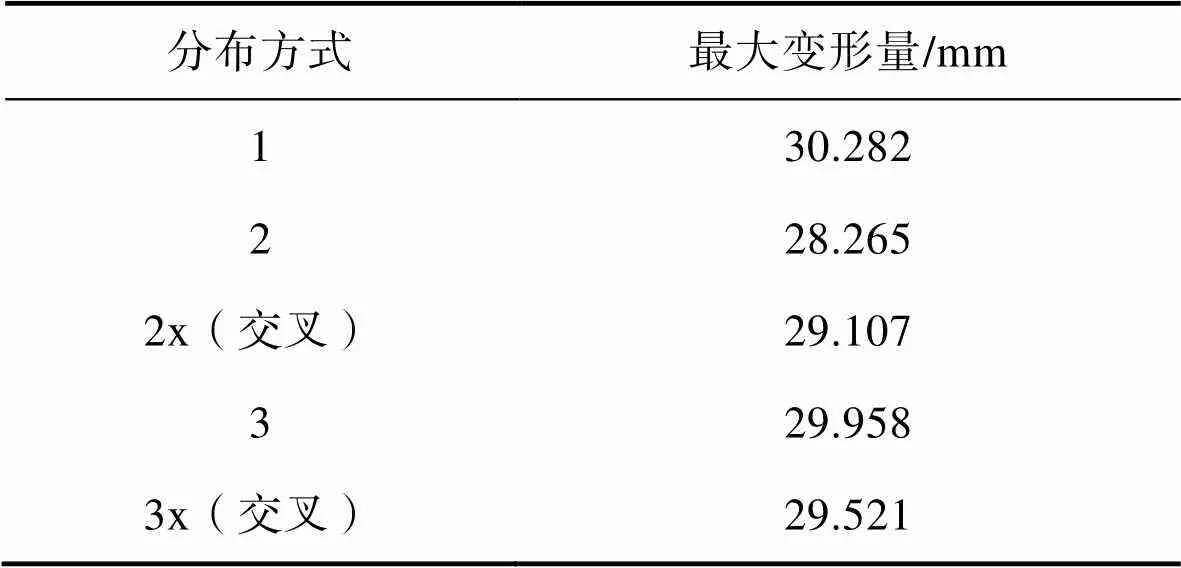
表4 不同開槽分布時(shí)襯墊的最大變形量

2.2.2 最大等效應(yīng)力分析

厚度為50 mm，不同開槽分布的緩沖襯墊的最大等效應(yīng)力見表5。當(dāng)開槽呈交叉分布時(shí)（2個(gè)交叉開槽、3個(gè)交叉開槽），緩沖襯墊與產(chǎn)品接觸的角部存在應(yīng)力集中，容易損壞產(chǎn)品。平行開槽時(shí)，2個(gè)平行槽的緩沖襯墊的等效應(yīng)力最大，為0.103 61 MPa，1個(gè)槽的緩沖襯墊的等效應(yīng)力最小，為0.096 81 MPa，說明1個(gè)槽時(shí)產(chǎn)品所受到襯墊的等效應(yīng)力最小，能夠很好地保護(hù)產(chǎn)品。

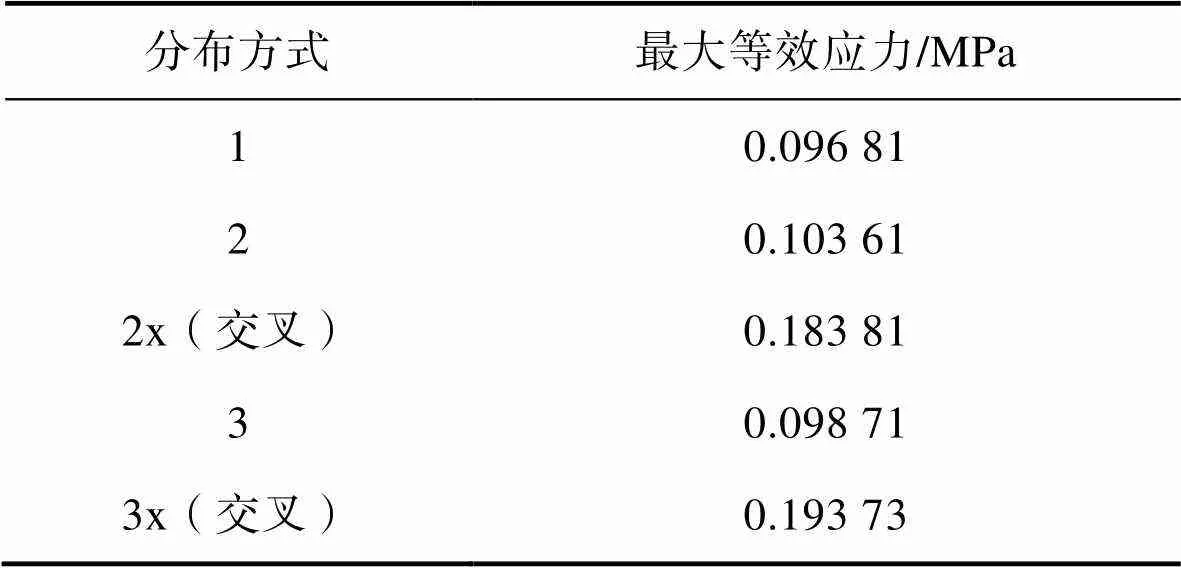
表5 不同開槽分布時(shí)襯墊的等效應(yīng)力

2.2.3 速度分析

厚度為50 mm，不同開槽分布的緩沖襯墊緩沖時(shí)，產(chǎn)品的速度變化見圖10。3個(gè)平行槽分布的襯墊緩沖后，產(chǎn)品最終的速度最小，這是由于此結(jié)構(gòu)緩沖時(shí)，中間2塊泡沫受到?jīng)_擊時(shí)發(fā)生瞬間失穩(wěn)現(xiàn)象，導(dǎo)致其他接觸面上吸收了更多的彈性勢(shì)能，響應(yīng)也損失了更多的沖擊能量。其余結(jié)構(gòu)襯墊緩沖后產(chǎn)品的速度變化相差很小。不同開槽分布的緩沖襯墊被壓縮到極限時(shí)所經(jīng)歷時(shí)間分別為0.008 54，0.008 64，0.008 83，0.009 07，0.008 93 s，其中時(shí)間變化相差最大為5.84%，襯墊壓縮到極限所用的時(shí)間相差較小，可忽略不計(jì)。

圖10 不同開槽分布襯墊緩沖時(shí)產(chǎn)品的速度變化

3 結(jié)語(yǔ)

文中研究了不同梯形槽底角和梯形開槽分布的緩沖襯墊受到?jīng)_擊時(shí)的最大變形量、最大等效應(yīng)力和沖擊后產(chǎn)品的速度，可得出以下結(jié)論。

1）通過建立產(chǎn)品襯墊緩沖系統(tǒng)，用仿真模擬的方法計(jì)算產(chǎn)品從800 mm高度跌落時(shí)的緩沖襯墊變形量、產(chǎn)品的速度、加速度。將有限元分析結(jié)果與沖擊理論模型計(jì)算結(jié)果進(jìn)行對(duì)比，二者符合程度較好，驗(yàn)證了有限元模型計(jì)算的可靠性。

2）等效接觸面積相同，底角小于70°時(shí)，緩沖結(jié)構(gòu)整體剛度過小，襯墊結(jié)構(gòu)存在不穩(wěn)定現(xiàn)象，導(dǎo)致跌落時(shí)產(chǎn)品觸底，不能很好地保護(hù)產(chǎn)品。當(dāng)?shù)捉谴笥?0°時(shí)，底角為85°的緩沖襯墊等效應(yīng)力最小，為0.0966 MPa，并且產(chǎn)品的速度改變量最小因此在結(jié)構(gòu)設(shè)計(jì)時(shí)，底角85°的結(jié)構(gòu)作為底角的最佳參考值。

3）等效接觸面積相同，底角為90°時(shí)，1個(gè)槽緩沖襯墊最大變形量，為30.282 mm，等效應(yīng)力為0.096 81 MPa，所以1個(gè)槽緩沖結(jié)構(gòu)保護(hù)產(chǎn)品的能力最佳。該研究結(jié)果可用于包裝設(shè)計(jì)環(huán)節(jié)，以實(shí)現(xiàn)緩沖材料的減量化設(shè)計(jì)，以及最佳保護(hù)性能的目標(biāo)。

[1] 楊杰, 付志強(qiáng), 張蕾, 等. EPE動(dòng)態(tài)沖擊曲線擬合函數(shù)對(duì)比[J]. 包裝工程, 2021, 42(9): 32-36.

YANG Jie, FU Zhi-qiang, ZHANG Lei, et al. Comparison of EPE Dynamic Impact Curve Fitting Function[J]. Packaging Engineering, 2021, 42(9): 32-36.

[2] 苗紅濤. EPE泡沫塑料在多次沖擊下的緩沖性能[J]. 包裝工程, 2017, 38(5): 111-114.

MIAO Hong-tao. EPE Foam Cushioning Performance under Repeated Dropping Shocks[J]. Packaging Engineering, 2017, 38(5): 111-114.

[3] GE Chang-feng, HUANG Hao-qi. Corner Foam Versus Flat Foam: An Experimental Comparison on Cushion Performance[J]. Packaging Technology and Science, 2015, 28(3): 217-225.

[4] 宋曉利, 劉全校, 張改梅, 等. 重疊結(jié)構(gòu)緩沖材料緩沖性能分析[J]. 北京印刷學(xué)院學(xué)報(bào), 2016, 24(2): 14-16.

SONG Xiao-li, LIU Quan-xiao, ZHANG Gai-mei, et al. Analysis of Cushioning Properties for Cushioning Materials with Overlapping Structures of EPE and EPS Via Finite Element Method[J]. Journal of Beijing Institute of Graphic Communication, 2016, 24(2): 14-16.

[5] 田芃, 滑廣軍. 尺度效應(yīng)對(duì)發(fā)泡聚乙烯靜態(tài)緩沖性能的影響[J]. 包裝學(xué)報(bào), 2013, 5(4): 30-33.

TIAN Peng, HUA Guang-jun. Impact of Scale Effect on Cushioning Properties of Expanded Polyethylene[J]. Packaging Journal, 2013, 5(4): 30-33.

[6] MüLKO?LU O, GüLER M A, ACAR E, et al. Drop Test Simulation and Surrogate-Based Optimization of a Dishwasher Mechanical Structure and Its Packaging Module[J]. Structural and Multidisciplinary Optimization, 2017, 55(4): 1-18.

[7] OZTURK U E, ANLAS G. Finite Element Analysis of Expanded Polystyrene Foam under Multiple Compressive Loading and Unloading[J]. Materials and Design, 2010, 32(2): 773-780.

[8] MILLS N J, MASSO-MOREU Y. Finite Element Analysis (FEA) Applied to Polyethylene Foam Cushions in Package Drop Tests[J]. Packaging Technology and Science, 2005, 18(1): 29-38.

[9] ROLAND U, KARTHIK A S, TJORBEN B, et al. Finite Element Analysis Considering Packaging Efficiency of Innovative Battery Pack Designs[J]. International Journal of Crashworthiness, 2020, 25(6): 664-679.

[10] 盧富德, 滑廣軍, 王麗姝, 等. 梯形聚乙烯泡沫結(jié)構(gòu)動(dòng)態(tài)壓縮響應(yīng)有限元分析[J]. 振動(dòng)與沖擊, 2019, 38(14): 234-238.

LU Fu-de, HUA Guang-jun, WANG Li-shu, et al. Finite Element Analysis of Dynamic Compression Response of Trapezoidal Polyethylene Foam Structure[J]. Journal of Vibration and Shock, 2019, 38(14): 234-238.

[11] 李志強(qiáng), 靳朝暉, 張素風(fēng), 等. 正棱臺(tái)緩沖墊結(jié)構(gòu)參數(shù)對(duì)靜態(tài)緩沖性能的影響[J]. 包裝工程, 2020, 41(7): 141-146.

LI Zhi-qiang, JIN Zhao-hui, ZHANG Su-feng, et al. Influence of Structural Parameters of Prism Cushion on Its Static Cushioning Property[J]. Packaging Engineering, 2020, 41(7): 141-146.

[12] 李淑娟, 仲晨, 張居中. 異型緩沖墊的靜態(tài)緩沖性能[J]. 包裝工程, 2017, 38(3): 41-45.

LI Shu-juan, ZHONG Chen, ZHANG Ju-zhong. Static Cushioning Performance of Irregular-Shaped Cushions[J]. Packaging Engineering, 2017, 38(3): 41-45.

[13] 李國(guó)志, 劉鴻梅, 孫德強(qiáng), 等. 步進(jìn)電機(jī)驅(qū)動(dòng)器和EPE襯墊配合間隙與振動(dòng)關(guān)系[J]. 包裝工程, 2021, 42(5): 142-147.

LI Guo-zhi, LIU Hong-mei, SUN De-qiang, et al. Relationship between Vibration and Fit Clearance of Stepper Motor Driver and EPE Cushion Foam[J]. Packaging Engineering, 2021, 42(5): 142-147.

[14] 馮紅蜻, 侯瓊, 任慧慧. EPE結(jié)構(gòu)因素對(duì)靜態(tài)緩沖性能影響的仿真與試驗(yàn)分析[J]. 上海包裝, 2021(1): 34-38.

FENG Hong-qing, HOU Qiong, REN Hui-hui. Simulation and Experimental Analysis of the Influence of EPE Structural Factors on Static Cushioning Performance[J]. Shanghai Packaging, 2021(1): 34-38.

[15] GB/T 8168—2008, 包裝用緩沖材料靜態(tài)壓縮試驗(yàn)方法[S].

GB/T 8168—2008, Testing Method of Static Compression for Packaging Cushioning Materials[S].

[16] GB/T 4857.17—2017, 包裝運(yùn)輸包裝件基本試驗(yàn)第17部分: 編制性能試驗(yàn)大綱的通用規(guī)則[S].

GB/T 4857.17—2017, Packaging Basic Tests for Transport Packages Part 17: General Rules for the Compilation of Performance Test[S].

[17] 湯伯森. 包裝動(dòng)力學(xué)[M]. 北京: 化學(xué)工業(yè)出版社, 2011: 45-49.

TANG Bo-seng. Dynamics of Package Cushioning[M]. Beijing: Chemical Industry Press, 2011: 45-49.

Finite Element Optimization Design of Trapezoidal Slot Polyethylene Cushion

LI Guo-zhi1,2,3, DUAN Mao-mao1,2,3, LUO Zhi-yao1,2,3, SUN De-qiang1,2,3

(1.Shaanxi University of Science and Technology, Xi'an 710021, China; 2.Key Lab of Functional Printing and Transport Packaging of China National Light Industry, Xi'an 710021, China; 3.National Demonstration Center for Experimental Light Chemistry Engineering Education, Xi'an 710021, China)

The work aims to explore the dynamic cushioning performance of trapezoidal slot EPE cushion and optimize the cushion structure, so as to provide a scientific reference scheme for subsequent design of cushion structure. With 23 kg/m3EPE as the test material, the static compression test was carried out on the samples, and the stress-strain data were obtained by data processing and imported into the material library of Ansys Workbench, to simulate the finite element impact on the product-cushion system. The theoretical calculated results of impact were compared with the results of finite element analysis. Then, the equivalent contact area remained unchanged and the maximum deformation, equivalent stress, velocity and other data were obtained through the finite element simulation on the product-cushion system with different base angle and slotting distribution. When the base angle was less than 70°, the stiffness of cushion structures was too small, resulting in the product hitting the ground during falling, which could not protect the product well. When base angle was greater than 70°, thedegreeof85° had thelowestequivalentstressof0.0966MPa, andtheproducthadthesmallestchangein velocity. When the base angle was 90°, thedeformationofoneslotwasthelargest,andthevalue was 30.282 mm, and the equivalent stress was 0.096 81 MPa. Therefore, in structural design, the cushion structure with a base angle of 85° and one slot can be regarded as the best reference value to achieve the reduction design of cushioning materials and the best protection effect of materials.KEY WORDS: polyethylene foam; cushioning packaging; trapezoidal; dynamic cushioning property

TB485.1

A

1001-3563(2022)01-0133-08

10.19554/j.cnki.1001-3563.2022.01.017

2021-09-10

國(guó)家自然科學(xué)基金（51575327）；陜西省教育廳重點(diǎn)實(shí)驗(yàn)室及基地項(xiàng)目（16JS014）；陜西省教育廳2014陜西本科高校專業(yè)綜合改革試點(diǎn)子項(xiàng)目（陜教高[2014]16號(hào)）

李國(guó)志（1979—），男，陜西科技大學(xué)副教授，主要研究方向?yàn)榫彌_包裝動(dòng)力學(xué)、運(yùn)輸包裝及包裝結(jié)構(gòu)設(shè)計(jì)。

孫德強(qiáng)（1976—），男，陜西科技大學(xué)教授、博導(dǎo)，主要研究方向?yàn)榘b系統(tǒng)的結(jié)構(gòu)、性能與設(shè)計(jì)。