多級變胞機構的剛度調控分析

李延斌， 劉 濤，， 劉玉旺， 葛 壯， 苑婷雯

(1. 沈陽工業大學 機械工程學院， 沈陽 110870； 2. 中國科學院沈陽自動化研究所 機器人學國家重點實驗室， 沈陽 110016)

連續型多級變胞機構具有很強的自適應性和避障能力，受到國內外學者的關注[1].單電機驅動連續型伸縮機械臂，因其特有的剪叉機構構型，既保留了連續型機械臂的靈活特性，同時具備自由伸縮功能，適應更加多樣化的復雜環境[2].但目前關于多級變胞機構的剛度調控研究還較少.

Qi等[3]介紹了串聯雙層平面彈簧的連續體機械手結構設計；Chautems等[4]基于相變材料設計了一個用于微創手術的變剛度磁性連續裝置；Chu等[5]提出了針對欠驅動方式的彈簧設計參數的度量標準；屈淑維等[6]提出對串聯機械臂系統誤差和隨機誤差進行分析的方法；Xu等[7]介紹了繩索驅動的超冗余柔性臂；Cui等[8]考慮了彈簧的參數對抓取范圍的影響以及彈簧對自適應性的影響，通過量化突出了分析方程，對彈簧的抓取穩定性進行了分析；Dalibor等[9]提出了一種自適應抓取機器人來檢測和識別物體的方法，并優化了基于傳感器反饋算法來實現物體抓取；王宏等[10]對機器人導航中振動檢測傳感器的反饋做了研究；曹燕飛等[11-12]介紹了一款用于微創手術的連續型機器人，通過驅動布置在連接器上的柔性電纜，來實現整體臂的彎曲；彭鶴等[13]介紹了具有一定避障和過彎能力，可以完成油氣管道特殊工況下的檢測和維修的爬行機器人；Yang等[14]介紹了一種利用彈性材料合金驅動桿提供運動的連續體機器人；張瀟等[15]利用虛功原理對復合剪叉式機械臂進行力學建模，并對剪叉臂在極限情況下的受力情況進行分析.

綜上所述，學者們對變胞機構的機構學和運動學開展了較為廣泛的研究，取得了大量的研究成果.但對多級變胞機構的剛度調控機理方向還未進行深入系統研究，尚未有該類機器人的剛度調控策略，而剛度調控策略作為實現多級變胞機構的關節柔順性，提高多級變胞機構的集成度，實現多級變胞機構緊湊化的一種重要方法，對其進行深入研究對于多級變胞機構機器人更好地走進人們的日常生活有著十分重要的意義.

本文針對一種新型單電機驅動多級變胞象鼻機器人開展剛度調控研究工作.根據結構之間的相似關系，將該多級變胞機構離散化為8個單元，通過單級變胞機構對包含彈簧在內的單元進行力學建模與力學特性分析，建立了多級變胞機構的力學模型，然后基于單級變胞機構的剛度分析，進而得到多級變胞機構的剛度分析結果，最后基于實驗測試數據可以對彈簧的安裝位置、彈簧的安裝角度以及彈簧剛度等特性進行確定，最終實現了多級變胞機構的性能最優化.

1 靜力學分析

象鼻機器人由9個單元組成，其中第一單元為基本單元，其他8個為驅動單元，由上至下分別為第一單元至第八單元，僅由一個電機驅動.這9個單元可以實現平面內的彎曲和拉伸運動，使機器人能夠保持各種形態，如圖1a所示.象鼻機器人由多級變胞機構組成，由于剛度調控彈簧的存在，在彎曲過程中，當變形機構與物體接觸時，相應的變形機構會發生自適應變形，如圖1b所示.

由于多級變胞機構是由多個單級變胞機構串聯組成的，在分析多級變胞機構力學特性時，需考慮到各個單級變胞機構力學特性的傳遞，故采用先局部再整體的方法，先對單級變胞機構進行分析.表1為變量符號定義表.

圖1 象鼻機器人結構圖Fig.1 Structure of elephant-trunk robot

1.1 單級變胞機構的力學分析

當多級變胞機構抱持物體時，在各級變胞機構適應不同形狀的物體過程中，各級變胞機構中的彈簧也會發生變形，在分析時，首先針對單級變胞機構進行分析，最后一級變胞機構受力圖如圖2所示.設AE長度為l4，彈簧的形變量為

Δx=x0-l3

(1)

彈簧的彈力為

F彈=kΔx=k(x0-l3)

(2)

所以，A點的力矩平衡方程為

F彈sin∠GFA·l1=FNl4

(3)

可得

表1 變量符號定義Tab.1 Variable symbol definition

(4)

圖2 最后一級變胞機構受力圖Fig.2 Force diagram of last stage metamorphic mechanism

1.2 多級變胞機構的力學分析

多級變胞機構各級之間采用串聯方式進行連接，各級之間的連接點為A、B兩點，其在抱持物體時的受力狀態如圖3所示.

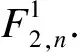
圖3 多級變胞機構之間的力學關系Fig.3 Mechanical relationship among multi-stage metamorphic mechanisms

2 剛度分析

在抱持不同形狀與尺寸的物體過程中，每個單級變胞機構也會受到與物體直接接觸的支持力與摩擦力的作用，其內部也存在著柔性的彈簧與剛性的連桿之間的耦合，同時，由于自適應力的大小與彈簧剛度、長度以及安裝位置均存在著密不可分的聯系，因此，對于彈簧的自身參數以及安裝參數的確定極為重要.可以將單級變胞機構作為模型，對其進行彈簧剛度與自適應特性之間關系的確定，將不同級變胞機構的參數代入，進而可以求出各級變胞機構的最佳彈簧剛度.

2.1 單級變胞機構的剛度分析

本文所提出的多級變胞機構每個單元的底部連桿和支撐連桿均有可供調節彈簧位置的安裝孔，通過對彈簧位置的調節可以得到不同的抱持曲線.圖4為單級變胞機構在彎曲抱持時的受力分析.

圖4 力關系圖Fig.4 Force relation diagram

由于每一單元結構相同，故只需仿真其中某一個單元即可，圖4中，負載為F′，E點為載荷作用點，l3則由負載決定，由于l1和l2位置固定，設AE的長度為l4，∠GFA為θt，則角度θt由l3決定，其他參數均可由測量獲得.

當某一關節在自適應過程中處于平衡狀態時，此關節存在如下關系：

(5)

(6)

由以上兩個公式可以得出負載與彈簧的剛度系數，負載與角度之間的關系為

(7)

(8)

2.2 多級變胞機構的剛度分析

多級變胞機構剛度調控的任務可以分為兩部分：一部分是對各級變胞機構中的彈簧長度、安裝位置等相關幾何關系的確定；另一部分是對各級變胞機構中的彈簧剛度進行確定.

2.2.1 彈簧長度和安裝位置的幾何關系分析

首先針對單級變胞機構進行分析，如圖4所示，設彈簧的原長為x0，彈簧的剛度系數為k，∠GFA接近90°時，彈簧彈力用于抵抗自適應變形時的分配比例最大，由余弦定理可得

(9)

因為l3為彈簧在自適應過程中的長度，而彈簧是標準件，因此彈簧的長度是規定好的，因此，需要確定l1、l2與∠GFA的關系.

由于各級變胞機構中存在比例關系，可以確定各級中θt的大小是不變的，取第一級變胞機構支撐連桿的長度為a，則第n級變胞機構中支撐連桿的長度為apn-1.以最后一級變胞機構為例，則有

a8=ap7=80×0.957=55.87 mm

(10)

取l3的原長小于a8，經過查閱機械設計手冊，取l3=35 mm，由于彈簧的最大壓縮量為自身長度的30%，因此，彈簧的最短長度為24.5 mm.

經過對l3長度相關參數的確定，可以得到l1、l2與∠GFA的關系，如圖5所示.

為了保證彈簧彈力沿著底部連桿方向的分力與接觸點處的摩擦力可以相互抵消一部分，進而可以減小對于連接軸的壓力，故需要保證0°<φ1<90°，可得

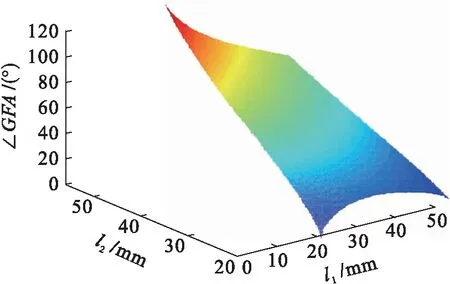
圖5 l1、l2與∠GFA的關系曲面Fig.5 Relation surface of l1，l2 and ∠GFA

(11)

同樣可以得到l1、l2與φ1的關系，如圖6所示.

圖6 l1、l2與φ1的關系曲面Fig.6 Relation surface of l1，l2 and φ1

由上述兩幅曲面圖可知l1、l2與∠GFA、φ1的關系，為了確定最優位置，需要將兩幅曲面圖進行合并，由于∠GFA和φ1的角度范圍存在偏差，因此選擇將∠GFA的角度減小50°(此角度為自己設定的角度，目的為利用圖解法方便求解，只需要后期將其換算回來即可)，其結果如圖7所示.兩平面相交的交線正是在同一變胞機構中安裝位置l1、l2相同的情況下，分別對應的∠GFA和φ1.

圖7 兩平面的相交曲面Fig.7 Intersection surface of two planes

2.2.2 彈簧剛度分析

關于各級變胞機構中彈簧剛度的確定，前文已經將多級變胞機構之間內部傳遞的力進行了求解，因此，可以將單級變胞機構作為模型，對其進行彈簧剛度與自適應特性之間關系的確定，進而將不同級變胞機構的參數代入，可以求出最佳的彈簧剛度.其中，彈簧彈力F彈與接觸點處的正壓力FN之間的關系為

F彈sin∠GFA·l1=FNl4+FDc

(12)

變形可得

(13)

式中，ci為第i級變胞機構底部連桿的長度.

2.3 剛度調控特性參數確定

2.3.1 彈簧安裝位確定

1) 第八級變胞機構中彈簧安裝位置的確定.經過針對兩個曲面交線的確定，可得交線上21 805個數據滿足要求，初始位置時，l3=35 mm，φ1=30.1°，∠GFA=80.1°；末態位置時，l3=24.5 mm，φ1=53.4°，∠GFA=104.1°.由以上數據可得φ1與l3之間的關系如圖8所示.

圖8 包絡角φ1與安裝位置l3的關系曲線圖Fig.8 Relation curve between envelop angle φ1 and installation site l3

由φ1與l3的關系曲線圖可知，在l3的整個變化過程中，φ1值一直在(0°，90°)的范圍內，因此滿足結構上的要求.∠GFA與l3之間的關系如圖9所示.

圖9 l3與∠GFA的關系曲線圖Fig.9 Relation curve between l3 and ∠GFA

由于要求∠GFA的大小盡量在90°附近，由l3與∠GFA的關系曲線圖可知，∠GFA的變化范圍為(80°，105°)之間，基本在90°附近變化.同時，為了提供較大的包絡角φ1，故選取圖7的末態極限位置作為安裝位置，此時在圖7中對應的數據為l1=26.08 mm，l2=39.89 mm.故l1=26.08 mm，l2=39.89 mm為第八級變胞機構中彈簧的最佳安裝位置.

2) 其他級變胞機構中彈簧安裝位置的確定.按上述方法類推即可，同時根據仿生象鼻各關節的真實比例系數，得出各級變胞機構的相關位置參數如表2所示.

表2 各級變胞機構的彈簧安裝參數Tab.2 Spring installation parameters of metamorphic mechanisms at all levels

彈簧的安裝位置固定，此時，彈簧的最大壓縮量也就固定了，因此，當變胞機構承擔負載時，可以選擇剛度系數不同的彈簧，對不同質量的物體進行自適應調整.

2.3.2 彈簧剛度確定

經過查閱資料可知，設最大壓縮量與自身長度的比值為h，故當彈簧達到最大壓縮量時，存在

l3=(1-h)x0

(14)

故方程可以寫成

(15)

在第n+1級中

(16)

1) 第八級變胞機構中剛度的確定.彈簧剛度與負載之間的關系為

(17)

為了保證在工作過程中的可靠性，需要選擇φ1的最大值，因此取φ1=53.4°的情況進行分析，l4應取最大值即55.87 mm進行分析.

將相關參數代入后，可得

k=0.21FN

(18)

取第八級所承受的最大正壓力為10 N，可得到關系曲線如圖10所示.

圖10 正壓力與彈簧剛度系數關系曲線Fig.10 Relation curve of positive pressure vs.spring stiffness coefficient

由于在自適應過程中，φ1的大小是不斷變化的，因此彈簧剛度也會與φ1存在一定的關系.

同時，由余弦定理可得

根據當前國家和教育部的要求，職業教育就是要培養高技能型人才，提高學生的實踐能力和對工作的適應能力。這就要求我們職業教育的過程更加貼近工程實踐，要求我們的課程教學更能體現實踐要求。

(19)

又有

(20)

將式(14)～(18)與式(20)進行聯立可得

(21)

將相關參數代入，取負載為最大正壓力10 N，可得到關系曲線如圖11所示.

圖11 l3與彈簧剛度系數關系曲線Fig.11 Relation curve of l3 vs.spring stiffness coefficient

綜上所述，當取底部連桿最遠端的正壓力為10 N時，可得彈簧剛度系數為4.28 N/mm.

2) 其他級變胞機構中剛度的確定.除最后一級變胞機構外，其他級變胞機構所承受的負載還會有一部分是從后一級變胞機構傳遞過來的，從安全性的角度出發可得

(22)

將F彈，i=ki(x0，i-l3，i)代入可得

(23)

由于第八級變胞機構的約束反力已經求出，而其他相關參數已知，故可由式(23)對彈簧剛度進行求解.由于各級變胞機構之間為等比數列的關系，因此分析過程都是相似的，在第八級變胞機構分析基礎上進行變形，所得結果如表3所示.取底部連桿最遠端的正壓力為10 N時為最大負載的狀態.

表3 彈簧剛度系數與力學數據Tab.3 Spring stiffness coefficient and mechanical data

3 剛度分析實驗

3.1 驗證安裝位置l3與彈簧剛度系數k的關系

針對彈簧剛度與彈簧壓縮量之間的關系以及最末級變胞機構進行實驗分析，在最后一級變胞機構最末端施加10 N的力，對于不同剛度的彈簧，測量其壓縮量的大小，并與理論計算所得結果進行對比，進而對理論計算進行驗證.

圖12 l3和k的實驗與理論結果對比Fig.12 Comparison between experimental and theoretical results for l3 and k

經過實驗可知，所得l3的長度與理論計算結果基本一致，l3與k為非線性關系.

3.2 驗證彈簧剛度系數k與正壓力FN的關系

采用的彈簧剛度系數分別為0.60、1.00、1.25、1.50、1.75、2 N/mm，選擇彈簧的壓縮量為10.5 mm，實驗過程如圖13所示.實驗數據與理論計算結果的對比如圖14所示.

經過實驗可知，所得力的大小與理論計算結果基本一致，FN與k為線性關系.

4 結 論

本文建立了多級變胞機構的力學模型，在此基礎上分析了多級變胞機構之間力的傳遞特性，進而對多級變胞機構整體力學特性進行分析與求解，同時分析了彈簧剛度、彈簧安裝位置以及安裝角度對剛度調控特性的影響，最后通過實驗驗證了理論結果的正確性，并得出以下結論：

1) 多級變胞機構剛度調控的任務可以分為兩部分，一部分是對各級變胞機構中彈簧長度、安裝位置等相關幾何關系的確定；另一部分是對各級變胞機構中彈簧剛度進行確定.

圖13 實驗過程圖Fig.13 Experimental process diagram

圖14 FN和k的實驗與理論結果對比Fig.14 Comparison of experimental and theoretical results for FN and k

2) 在一定范圍內，最佳彈簧剛度隨著安裝位置l3的增大而減小，當最佳彈簧剛度達到最小值后，最佳彈簧剛度隨著安裝位置l3的增大而增大，兩者之間為非線性關系.

3) 在分析多級變胞機構剛度調控問題時，可以取出單級變胞機構作為模型，對其進行彈簧剛度與自適應特性之間關系的確定，將不同級變胞機構的參數代入，進而可以求出最佳的彈簧剛度，本文所提到的多級變胞機構中的正壓力與彈簧剛度為線性關系.