基于城市水文模型模擬的暴雨積澇災害風險預警研究*

扈海波 孟春雷 程叢蘭 張西雅

北京城市氣象研究院，北京 100089

提 要： 以土地利用及土地覆蓋分類(透水及不透水地表組成)及格點化城市管網排水能力為水文模型主要輸入參數，以雷達反演及外推雨量為強迫，模擬城市地表水反應過程及水動力過程，提出在城市水文模型基礎上發展城市暴雨積澇風險預警及預報應用。水動力模型以二維淺水方程為基礎，用變向隱式法分別在x軸和y軸方向上分兩步求解差分方程。此演算方法具回水效應，間接實現了徑流路徑搜索的多重路徑尋向，還原城市地表徑流紊流、分流及散流較多的狀況。研究分別以在線及脫線方式做了基于城市水文模型的模擬及檢驗分析。在線模式研究以2012年北京“7·21”暴雨為個例，用雷達定量降水估計強迫到城市水文模型中演算網格積水深度， 模擬“7·21”暴雨積澇情景，發現模擬結果基本反映當天的積水及積澇發生情況；脫線模式模擬則側重計算城市地區不同風險等級暴雨積澇的臨界雨量值(風險閾值)，尤其是積澇易發點的風險閾值。研究推導出北京地區49個積澇易發點積水深度分別達到0.2、0.5、0.8和1.2 m時的1、3和6 h的臨界雨量，并以此作為北京地區暴雨積澇“藍黃橙紅”四個預警等級的劃定標準。

引 言

全球性城市化過程導致城市人口增多、城市面積迅猛擴張，致使城市成為一個巨大的承災體。這個巨大的承災體在面對自然災害的沖擊時，往往不堪一擊。其中極端暴雨導致的城市積澇已經并將持續地給全球城市帶來沖擊及影響，給人類帶來巨大的人員及財產損失(扈海波等,2013；Zhou et al,2013；Shepherd et al,2011)。

這促使眾多的氣象水文專家將研究的重點放在城市洪澇及積澇的風險識別、預警及預報上(Sharif et al，2006；He et al，2013；Moreno et al，2013)。而其中最為主流及最有應用前景的預報預警模式即為結合短時臨近預報系統及城市水文模型的開發應用(Ogden et al，2000；Smith et al，2005a；2005b；Vivoni et al，2006；Sharif et al，2006；Ntelekos et al，2006；Wright et al，2012；Barthold et al，2015)。其經典的流程方法是用雷達反演雨量強迫到城市水文模型，實時模擬城市地區未來的積水狀況(積水的深度及持續時間)來實施城市暴雨積澇風險預警及監控(趙琳娜等，2012；Smith et al，2005a；2005b；Silvestro et al，2017；Davolio et al，2017；Poletti et al，2019)，甚至是洪澇災害損失評估及預評估(Meyer et al，2009)。

這種預警模式能否成功應用的關鍵依賴于城市水文模型模擬輸出結果的有效性。此有效性包括積水模擬是否正確以及預警時間提前量能否滿足城市應急的需求(Sharif et al，2006)。實質上模型模擬的有效性根本依從于預報雨量的準確度(Silvestro et al，2017；Thorndahl，2017；Poletti et al，2019)。而預報雨量與應用效果之間的矛盾是預報提前量越大，其不確定性也越大，如強迫到水文模型中，效果不會太好(Kober et al，2012；Silvestro et al，2017；Thorndahl et al，2107)。只是預報提前量越大越滿足預警時效及應急準備的需求。以短時臨近預報系統的定量降水預報(QPFs)為例，此類數據在落區及雨量大小上普遍存有偏差，將其強迫到水文模型中，會產生讓現有的基于確定性模式的預報及預警作業無法承受的誤差(Kober et al，2012)。但QPF又有較理想的時間提前量，它對預警很關鍵。用QPF等外推及預報雨量做水文模型強迫的應用不是特別多(Silvestro et al，2017；Poletti et al，2019)。在特定個例情況下，如預報結果較好也會有不錯的應用效果，比如用融合了數值預報模式(NWP)雨量場的短時臨近預報做強迫的應用(Davolio et al，2017；Nerini et al，2017；Poletti et al，2019)。盡管提高QPF等雨量預報產品的質量對城市積澇預警很重要，但現有的短時臨近數值預報產品的質量很難突破到能一如既往地給第三方模型提供滿意強迫值的程度(Liechti et al，2013)。

盡管如此，短時臨近預報系統中較為精準的雷達降水估計(QPEs)，尤其是經過雨量站校準后，其雨量及落區準確度確實能滿足城市水文模型強迫的需求(Anagnostou and Krajewski，1998)，而模型輸出結果也會產生一定的時間提前量。Sharif et al(2006)認為城市水文模型與短時臨近預報產品的QPE結合進行城市積澇災害的預警也是可行的，因為積水過程的延遲效應會導致積水峰值明顯落后于降水峰值。根據Sharif et al(2006)的研究，一般的降水過程大概有20～40 min的積水延遲，這就是說即便用實況雨量來做積澇風險預警，也能達到一定的時間提前量。而20～40 min的提前量對一些應急能力較強的城市來說，還是能減緩不少積澇災害的影響及損失。盡管雨量實時強迫到水文模型的積澇預警模式具有此類優點，但其最終的模型輸出結果經由短時臨近系統處理，然后強迫到水文模型中，兩個模型的加工會加大輸出的不確定性(Amponsah et al，2016)。這將制約其在確定性預報及預警模式中的應用效果，尤其是在預報員無法把握模擬結果的情況下，甚至繁瑣的數據處理及對模型的不熟練操作，都會干擾到預報員的決策判斷而造成模型被嚴重閑置。Barthold et al(2015)及Herman and Schumacher(2018)等曾強烈呼吁氣象界專業人士需要與水文界專業人士合作，共同解決暴雨洪澇及城市積澇預報及預警難題。Barthold et al(2015)甚至認為正是由于積澇預警在技術應用層面上遭遇到水文學與氣象學上的難題及挑戰，從而使得積澇能為所欲為地成為最為致命的氣象災害，每年導致的人員傷亡甚至超過了臺風及龍卷。

除了用雨量實時強迫到城市水文模型作模擬的預警模式外，另一種脫機模式更值得應用及關注。美國國家天氣局(NWS)的積澇指導系統(FFGs及GFFG)就采取脫機運行方式，用水文模型反推及驗算可造成流域內暴雨積澇的1、3及6 h臨界雨量及臨界產流值(Thresh-R)并用做預警判斷(Ntelekos et al，2006；Barthold et al，2015)。FFG的臨界雨量的降雨持續時間分別對應雷達外推雨量的1、3及6 h 降雨時長，用于表述該時段流域可導致洪澇或積澇的臨界雨量(Georgakakos，1986)。NWS的天氣預報辦公室這樣做的目的是可對照雷達外推雨量做出預警及預報判定，便于實施極端暴雨洪澇及積澇災害的應急防控(Gourley and Vieux，2005)。FFGs臨界雨量值主要通過計算臨界產流來判定，此臨界產流由塊狀地表水文反應模型“Sacramento土壤濕度核算模型”推算(The Sacramento Soil Moisture Accounting model，SAC-SMA)(Carpenter et al，1999)，此模型以流域為核算單元。FFG建立了覆蓋全美的數千個不同匯水面積的流域臨界雨量(Gourley and Vieux，2005)。Schmidt et al(2007)提出用格點化的方法替換FFG使其成為GFFG(gridded FFG)。隨后NWS的河流預報中心(River Forecast Center，RFC)開發了GFFG并投入運行。GFFG使用了5年回歸期雨量在美國自然資源保護局(Natural Resources Conservation Service，NRCS)三角形網格單元的水文模型上計算得出。Barthold et al(2015)認為FFG及GFFG需要進一步被改進使其更加適合積澇應用，尤其要改變其塊狀水文模型的局限使其能基于QPF做對流尺度的積澇預報。至此，WRF的水文模塊WRF-Hydro著手發展用對流模型輸出及其集合預報雨量強迫到分布式水文模型的積澇預報應用(Gochis et al，2015)。

FFG及GFFG的應用現狀及發展趨勢給用城市水文模型脫機運行方式建立城市地區積澇預警模式提供了借鑒和參考。盡管二者在模型使用、數據基礎及預報空間尺度上表現不一，但脫機模式的優勢同樣能體現在城市積澇預警中。第一，臨界雨量閾值的概念和方法更適用于對城市積澇易發點(城市立交橋、十字路口、地勢低洼地帶等)的積澇監測及預警，要點是通過水文模型的脫機模擬分析可得出這些易發點可能發生各種程度的積水及積澇的雨量閾值。第二，通過脫機方式得出城市地區易發點的對應雷達外推1、3及6 h的臨界雨量，便于預報員做出預警選擇及判斷。除此之外，預報員還可依托不同的預報產品(NWP及融合NWP的預報雨量)，而不僅僅限于短時臨近預報產品，靈活地做出城市積澇的預警及預報(趙琳娜等，2012；Poletti et al，2019)。第三，利用城市水文模型的脫機運行方式可不受模型運行時效性及時間快捷性的限制及要求，甚至可不惜耗費巨大的計算時間及資源來搜索臨界雨量，因此可配置更高或超高分辨率的水文模型，使用更精致的空間尺度及更短的時間步長來模擬推導臨界雨量(Seo et al，2013)，最終滿足城市暴雨積澇預警及預報的要求。而且這種運行方式可避免城市水文模型實時運行帶來的時間延遲及數據解讀過程，有助于提高預報員的判斷及預警反應能力。

鑒于上文所論，本研究開發了高時空分辨率城市分布式水文模型，在研究區的城市空間面上模擬1、3及6 h的降水，并強迫到該模型。根據模型模擬出的易發積澇點的積水深度及狀況，給出不同預警級別的雨量閾值留做預警指導。在應用中發現其技術路線可行，并對模型模擬及實際應用效果做了初步的檢驗及分析。當然，這套城市暴雨積澇的預警及預報機制仍然需要在應用及實踐中進一步被驗證及發展，而從眾多的文獻中可覷見該模型方法是城市暴雨積澇預警及預報的發展及應用趨勢(Ntelekos et al，2006；Gourley and Vieux，2005；Barthold et al，2015；Herman and Schumacher，2018)，值得進一步被開發及應用。

1 數據資料

1.1 雷達反演資料

雷達QPE/QPF資料為水文模型強迫的常用雨量數據資源，因其與雨量站數據相比有更好的時空分辨率及空間連續覆蓋的優勢(van de Beek et al，2010)。研究用北京市氣象局瑞圖系統(RAMPS-in)的短時臨近預報資料做模型強迫。RAMPS-in提供511×581網格的1 km×1 km分辨率的1、3及6 h的QPE/QPF，時間分辨率為10 min。其雨量數據反演自京津冀地區的北京S波段(BJRS)、天津S波段(TJRS)、石家莊S波段(SJZRS)、張北C波段(ZBRC)及承德C波段(CDRC)雷達傳送的基數據(陳明軒等，2013)，該數值產品從空間上完整覆蓋北京區域。

雷達反演雨量由雷達反射率因子與降水估計之間的Z-R關系換算得到，并非直接觀測值。除雷達信號因受遮擋、虛假回波及回波噪音等的干擾，不同降水條件下的雨滴譜分布差異使得雷達降水估計的Z-R關系發生改變，其反演雨量需用雨量站數據做進一步的訂正(Anagnostou and Krajewski，1998)。因此自2012年，北京地區的雷達反演雨量用了近2 000 個經數據質量控制的自動站雨量做訂正。同時，1、3及6 h的QPFs與高分辨率的非靜態數值預報模式(NWP)雨量場作融合(Kober et al，2012)，融合結果減少了原本數據不確定性，提高了這類雨量預報數值產品的質量及可用性(Poletti et al，2019)。

這些QPEs/QPFs(包括融合產品)雨量數據用反距離插值(IDW)從1 km分辨率的Cartesian網格降尺度到30 m的城市水文模型網格，該30 m網格匹配水文模型采用DEM柵格數據，即可完成雨量數據對水文模型的對接或強迫。

城市水文模型模擬分析臨界雨量時，是用自定義雨量值為強迫，以遍歷方式模擬查證城市積澇易發點的臨界雨量值。原理上，暫不需要觀測雨量資料作強迫。但是基于實時監測的預報及預警模式仍需用雷達反演及外推雨量做強迫。

1.2 土地利用與土地覆蓋

水文模型使用的土地利用和土地覆蓋分類數據多從遙感資料中獲取(Velásquez et al，2020；Sy et al，2020)。遙感資料無疑是城市水文模型的重要數據源。對于現用的30 m網格高精度土地利用和土地覆蓋數據似乎不能完全取自遙感資料。本研究用國家測繪中心提供的2010年30 m×30 m分辨率的全球土地覆蓋產品(GlobeLand30)輔助提取城市不透水地表及透水地表類型。GlobeLand30產品主要源自Landsat TM/ETM+影像數據。2010年的GlobeLand產品還用中國環境及災害衛星(HJ-1)的影像數據輔助生成(Chen J et al，2015)。另外，其他類別的遙感影像也用來驗證及補充該分類產品，包括MODIS NDVI、全球測繪數據及DEM數據，以及線上的高分辨率影像，比如GoogleEarth影像、 Bing和OpenStreet 影像數據。GlobLand30有10種土地分類結果：耕地、森林、草地、灌木、濕地、水體、人工地面及裸地等，可用于提取透水及不透水地表組成。而用于城市水文模型參數輸入的30 m格點土地利用及土地覆蓋數據集除了必須有透水及不透水地表組成外，還應有地表水動力及與水文參數屬性相關的土地利用及土地覆蓋分類結果。遙感數據并不單獨提供或者完整覆蓋及替換此類數據。因此，北京市測繪局提供的2010年的1∶2 000高分辨率GIS基礎地理信息數據被用來補充提取所需要的土地利用及土地覆蓋數據(圖1)。

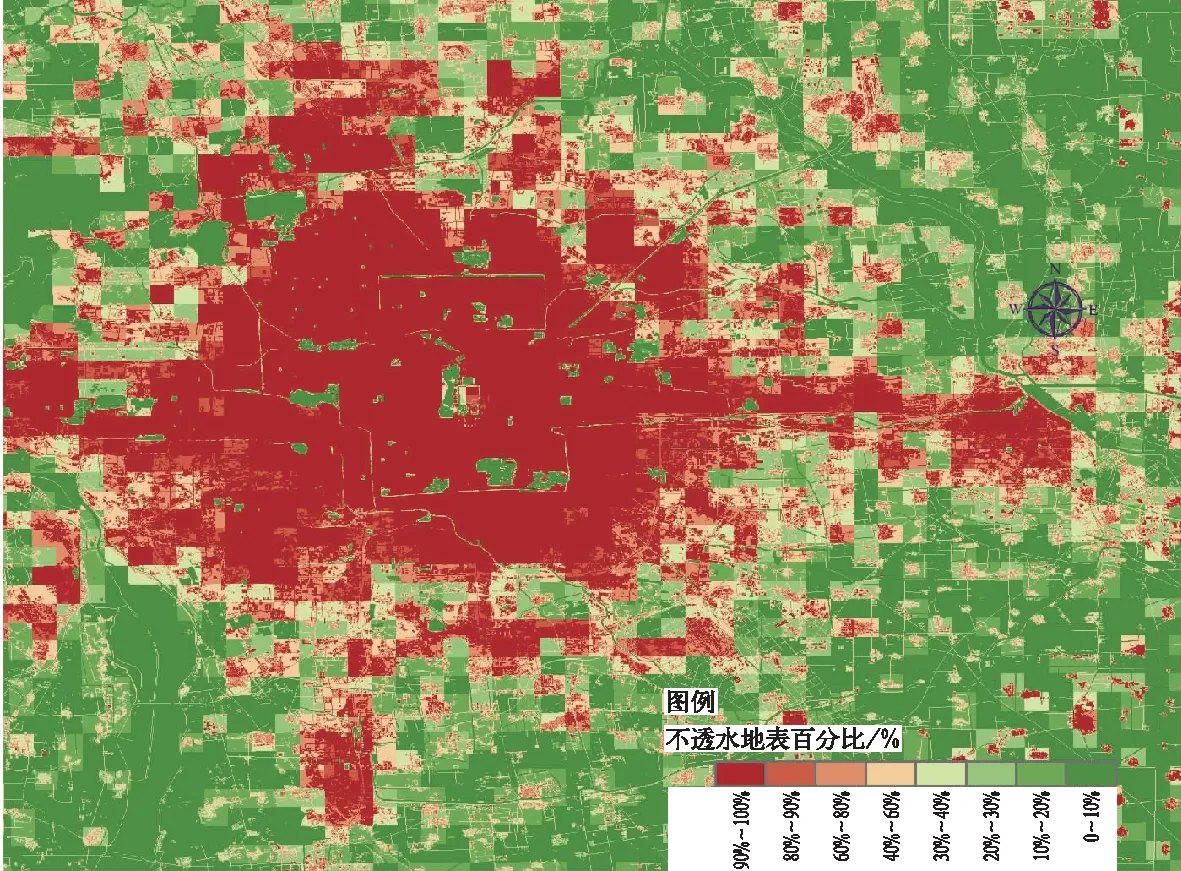
圖1 北京城市及近郊區不透水地表百分比分布Fig.1 Distribution of impervious surface area percent in Beijing urban， suburban and rurual areas

1.3 城市地區管網排水能力

城市排水管網的數據對城市水文模型的作用至關重要。GIS城市路網數據可用于提取網格化城市管網排水參數。提取的先決假定是城市排水管網常與路網平行修建，而管網的排水標準可參照GB50318—2017(中華人民共和國住房和城鄉建設部，2017),此標準定義了不同道路等級的管網排水能力(表1)。依此假定，能根據路網等級推算對應的管網排水能力。

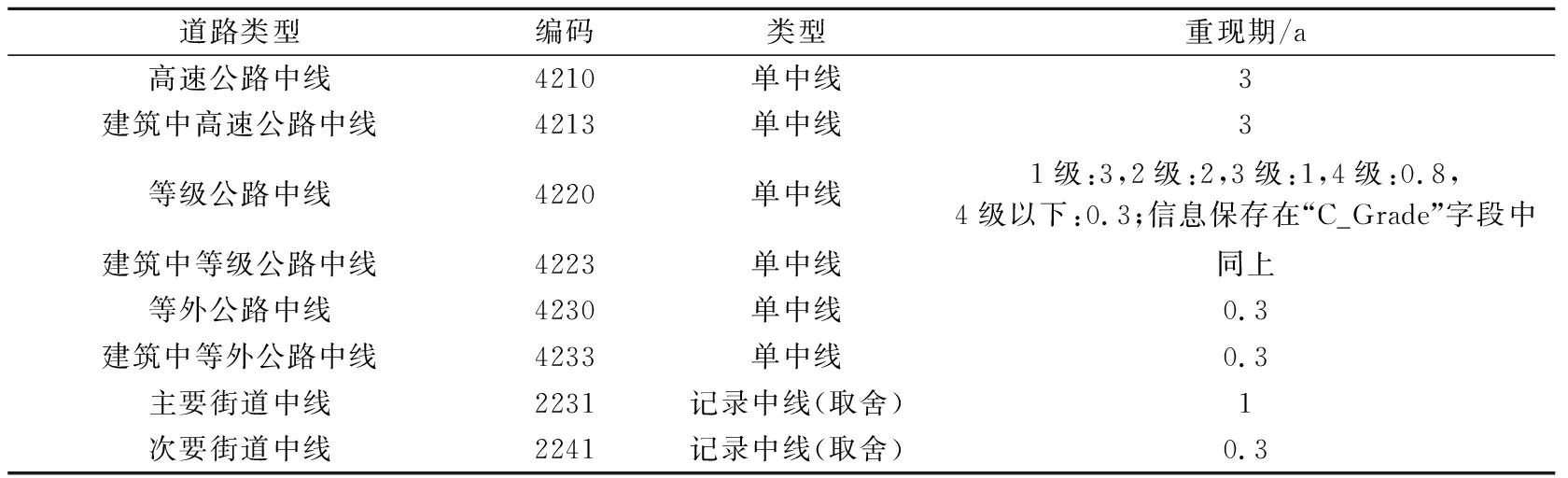
表1 不同道路類型下排水能力(重現期)的對應表(1∶2000地圖)Table 1 List of roadside pipes drainage capacities corresponding to road grades (mapscale of 1∶2000)

管網排水能力用設計重現期暴雨強度來度量(Zhu et al，2019)。Seo et al(2013)認為匯水接入城市管網系統的城市匯水區的匯流水量曲線變化直接影響排水管網的徑流量。城市排水管線系統的排水能力，原則上覆蓋環繞路網系統的GIS線型緩沖區域。因此水文模型網格單元的排水能力Dcell用網格單元幾何體與管線緩沖區做GIS疊加計算得到,即

(1)

式中：Inters[B(i)，Ocell]是GIS疊合操作用于計算第i個排水管線緩沖區B(i)與目標網格單元(Ocell)的疊加面積(單位：m2)；n是網格單元內的排水管線緩沖區數量(單位：個)；Dbuffer(i)為第i個排水管線的排水能力，常用暴雨重現期(單位：a)來表示該管線所能應對的地表產流量，具體計算參見2.2.1節；Acell為網格單元面積(單位：m2)。

上述方法依據路網的排水設計標準來提取管網的排水能力，間接獲得城市地區網格化管網排水能力。排水能力的網格化參數方案便于二維水文模型的演算，便于模型的功能實現及節省計算量，但在某種程度上會增大模型計算結果的不確定性。尤其是在有人為目標設定的情況下，比如主要積澇點在布設水泵的條件下，會導致模型模擬的結果存在其不能與實際積水狀況相吻合的情況。因此，在此建議如果在掌握了城市完整的排水管網及排水設施分布資料的前提下，可依據此類資料提取城市地區網格化管網排水能力指標值。如果只掌握部分“關鍵性”排水管網資料，建議可在路網資料提取的基礎上做適當的修正，減少數據的不確定性。圖2即為提取出的北京城區及近郊區的管網排水能力分布，也基本反映了市中心地區基礎設施較完善，管網排水能力稍強的基本狀況。

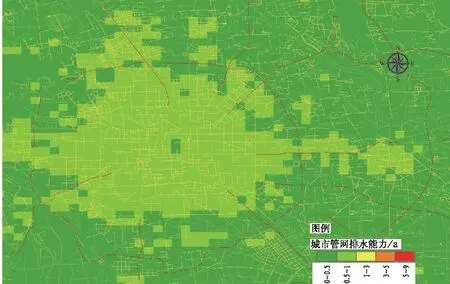
圖2 從GIS數據中提取出北京城市地區及近郊區以降雨回歸期為降雨強度度量的城市管網排水能力分布Fig.2 Distribution of the drainage capacity abstracted from GIS data， in terms of draining-out runoffs produced by certain return years rainfall intensities in urban, surrounding suburban and rural areas in Beijing

2 城市水文模型

城市水文模型主要包含三個子模型：(1)地表水反應模型用于推算產流量。產流分別在不透水地表及透水地表上生成。不透水地表上的產流生成可簡化為降水量減去地表洼蓄和蒸發量而得。透水地表產流則主要為Hortonian滲出(Velásquez et al，2020)。(2)徑流路徑搜索。(3)水動力模型。水動力模型以2D淺水方程為基礎模擬計算積水及積澇狀況。

2.1 城市地表產流計算

地表洼蓄主要包含地表吸管蓄水及重力填洼蓄水等(Velásquez et al，2020)，可依據地表土地利用與覆蓋類型給出經驗值。暖季降水的產流量會因蒸發出現輕微的變化，包括對土壤濕度及洼蓄的影響(Moreno et al，2013)，因此模型對產流的估算考慮地表水汽蒸發。蒸發量(E)的計算引用通用陸面模式(common land model，CLM)的子模塊來計算(Meng et al，2009)，就此將水汽蒸散納入產流的計算。在北京“7·21”特大暴雨個例研究中，CLM估算的降水蒸發量對不透水地表產流大致產生0.24 mm·(24 h)-1的削減量，而在有植被覆蓋的透水地表上的影響則較大，尤其在植被的蒸騰作用下可產生0.5 mm·h-1的蒸發量。

不透水地表產流Rp(單位：mm)可看作是降水量R(單位：mm)減去洼蓄Bg(單位：mm)及地表蒸發量E(單位：mm)：

(2)

對于透水地表的產流Ri(單位：mm)則由Horton模型算出地表下滲量f(單位：mm；Dooge，1992)，然后再減去蒸發及洼蓄：

(3)

需要注意的是上述的地表產流為未經由城市排水系統排泄的自然產流。地表產流減去城市排水后，產生地表徑流，在排水不良的地勢低洼處形成積水及積澇。

2.2 城市排水估計

2.2.1 雨強估計

雨強是估算城市排水能力的一個關鍵核算指標，一般用Chicago雨量圖方法(Chicago hyetograph mthod,CHM)推算回歸期內的暴雨雨強值序列而得出(Chen Y et al，2015)。局地雨強值由一定重現期的降雨率q(單位：mm·min-1) 來表示，用暴雨雨強公式估算(扈海波，2016；Zhu et al，2019)：

(4)

式中：t是降雨持續時間(單位：min)，P為暴雨重現期(單位：a)，A1、B、c及n為區域性暴雨強度特征相關的控制參數(均為無量綱參數，以下如無特別指出的均為無量綱值參數或系數)。A1為降雨參數(單位：mm)；c是降雨變化參數，b是降雨持續時間糾正參數，n是暴雨消減指數(與回歸期相關)。表2列出北京地區暴雨雨強估算的參數取值(A1、b、c和n)(扈海波，2016；Zhu et al,2019),而全國其他省(自治區、直轄市)城市規劃管理部門多根據本地區的暴雨強度特征頒布了不同標準(Zhu et al，2019)。

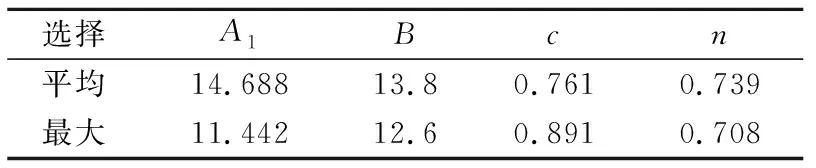
表2 北京地區暴雨雨強公式參數列表Table 2 Parameter values for the rainfall intensity of rainstorm formula

2.2.2 排水能力推算方法

排水能力指排水管網能有效應付一定重現期暴雨雨強的能力，重現期雨強值取決于地方性或區域性氣候特征，其計算公式定義為

Qs=q′ψF

(5)

式中：Qs為城市管網系統的設計排水流量(單位：L·s-1)，q′為對應的設計雨強(單位：L·s-1·hm-2)，ψ是產流系數，F為匯水面積(單位：hm2)。ψ控制地表產流量，其在不同土地利用和土地覆蓋類型上是不同的，取值可參見GB 50318-2017(中華人民共和國住房和城鄉建設部，2017)。

用式(4)和式(5)可推導出計算管網排水能力的設計雨量的公式：

(6)

這樣，城市地區單位時間產流rd(單位：mm·min-1)等于其透水地表及不透水地表上單位時間產流rs(單位：mm·min-1，其中rs=Rp+Ri)減去管網設計排水量q′，公式表述為：

(7)

2.3 城市地表徑流路徑選向

地表徑流路徑的搜索常用基于滑動窗口的D8算法(圖3a)，該算法在DEM中以單個高程格點八個方向的最大下降坡度作為徑流流向，以格點中心點的連線作為徑流路徑(Jenson and Domingue，1988)。Gallant and Hutchinson(2011)認為當徑流紊流和分流效應導致了徑流分散，坡度線和徑流線在水文地形形態上是不一樣的。在此情況下，多重徑流流向的尋徑才是描述徑流分散的關鍵及首選(Seibert and McGlynn，2007)。在算法實現上，多重徑流流向的判斷仍然可依據格點與周邊相鄰四個格點的坡度來確定，即水流從四個方向流向水位較低的格點(圖3b)。眾多文獻提到的LISFLOOD-FP模型就用這種四朝向分流算法(Bates and De Roo，2000；Zhu et al，2019)。此算法簡便，格點間產流的流出和流入依據與周邊格點的坡度來判斷。而徑流交換加快，格點間的水位變化會加快，這就要求水動力模型Manning水流的時間分辨率較高，不然容易產生徑流不連線性及偏差過大的情況(Hodges，2019)。D8算法和四流向算法的坡度線和對應的徑流網絡均可直接在DEM等高程數據的等高線上搜索得到(Moretti and Orlandini，2008)。除此之外，在水動力模型中加入回水機制，同樣可達到多重徑流的效果。Orlandini et al(2012)指出多重徑流算法所產生的徑流分流更多地受格點單元大小的限制，在使用該算法搜索徑流分散時需要反復對其檢驗及驗證。因此，Orlandini et al(2012)提出D8的改進算法(D8-LTD)，該算法通過徑流路徑規整及規劃，完善及優化了徑流路徑的生成，這樣D8-LTD算法除了保有路徑明確(確定及唯一性)、無分散、結果可靠及計算效率較高的優點外，還能近似在任何空間尺度上保持坡度線和徑流路徑的一致(Moretti and Orlandini，2008)。

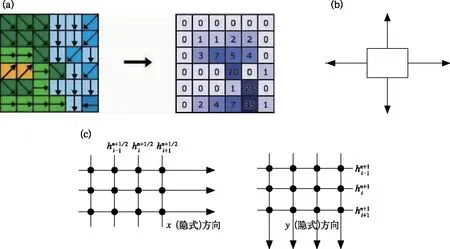
圖3 地表徑流路徑選向示意圖(a)D8算法，(b)四流向算法，(c)具有回水效應的水動力模型方法Fig.3 Diagram of urban surface flow routing methods(a) D8 method, (b) four-direction method, (c) hydraulic model inducing back water effects

盡管如此，本文認為在城市環境中，即便在地勢起伏不大而城市建筑等阻礙物較多的情況下，城市地表徑流的分散及紊流情況也會比較明顯及復雜。因此四朝向分流算法(圖3b)及2.4節介紹的具有回水計算過程的水動力模型(圖3c)比單路徑的D8算法更適用于城市水文模型的地表徑流路徑搜尋及水動力模型的計算。當然，為保證徑流的連續性特征，需要規劃水動力模型的時間步長。

2.4 城市水動力模型

城市水動力模型是城市水文模型的核心。此模型建于積水深度均一的二維淺水方程上。積水過程的淺水假設會降低模擬的準確性，增加模擬結果的不確定性和可接受程度。但是城市水文模型的模擬精度更多受數據不確定性的影響(比如地形參數和地表粗糙度等邊界條件的制約)，而動力過程的模型簡化對此的影響有限。這種非慣性及擴散波動模型可加入回水效應，實現多徑流尋向的效果。城市積澇的水流模式其實是介于分散波動和全動力方程之間。Bates and De Roo(2000)也認為城市積水的水動力過程可簡化為消除了局地加速、對流加速及對流壓力項的一維St.Venant方程，甚至假定摩擦與重力驅動是平衡的。

用淺水方程作為城市水動力模型基礎，其表述式如下：

連續方程為：

(8)

動力平衡方程為(x方向和y方向)：

(9)

(10)

式中：h是水位(水深加相對高程，單位：mm)；d是徑流深度(單位：mm)；t是徑流時間(單位：s)；u和v分別為在x方向和y方向上的徑流速度(單位：m·s-1)；Sfx和Sfy分別為在x方向及y方向上的摩擦坡度，g為重力加速度。摩擦項通過Manning公式計算，即：

(11)

(12)

式中：n為Manning系數。

在式(8)中q為潛層水流項，在城市水動力建模中假定為0。Seo et al(2013)認為在城市環境中透水地面被周邊不透水地面(水泥陸面及建筑物)阻斷的情況下，其部分下滲水流仍然會潛流到城市排水系統中，影響排水系統中匯流曲線10%的流量，因此提出了在城市排水模型系統中針對城市潛層水流的計算方法。但是對城市潛層水的估算非常復雜，即便出流到排水系統中，也對地表產流、積水及水淹狀況的影響不大。因此，此處仍然設定q值為0。

需要指出的是基于D8算法及四流向算法的水動模型，以單一格點為基本計算單元來核算其進水及出水量，而且假定摩擦與重力驅動是平衡的，再用Manning公式直接計算格點的進水及出水的流速(Bates and De Roo，2000)，那樣確實是簡化了計算。但在計算漫流過程中，比如用四流向算法，在單步執行時，隨著時間的推移，就會出現徑流交換加快，而只能限制模型的時間步長來減少計算偏差。當然時間步長越短，偏差就越少。因此，這里還是認為用有限差分的方法來計算水動力方程可暫時解決這個難題。

將式(8)改寫為以下離散方程：

(13)

x和y方向上的水動力平衡方程[式(9)、式(10)]分別可改寫為

(14)

(15)

將式(14)和式(15)簡化：gΔtSfx=uSx，gΔtSfy=vSy。

然后，將式(14)、式(15)分別代入式(13)整理后，可以得到類似下面的簡寫式

(16)

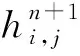
2.5 水動力模型時間步長的限定

用有限差分方法來計算格點的水位值，在淺水方程中水位的調整在x和y方向上進行，這種調整能夠體現徑流的回水效應，因此多重徑流方向的選取與四流向算法一樣。但四流向算法是直接用Manning公式來計算格點的進出水情況，就如同之前討論的那樣，必須限定水動模型的時間步長，而且由時間延遲產生的計算偏差隨時存在，延遲愈大偏差就越大。而有限差分方法雖然不會因時間步長的存在而產生偏差，但如果時間步長過大，會導致迭代計算失效，也就是這種ADI會導致計算不穩定(Caviglia and Dragani，1996)。因此，水動力模型的時間步長，需由式(17)作限定條件

(17)

式中：Δt為模型時間步長(單位：s)，Δx、Δy為在x和y方向上的格距，d為水深。

3 基于城市水文模型的暴雨風險預警實例應用及研究分析

城市水文模型的實例應用分為兩部分。一是模擬雷達反演雨量強迫到水文模型的在線運行方式。該方式依據實況運行得到的積水深度及水淹面積來做出積澇發生及發展的判斷及預警。二是用水文模型的模擬來搜索城市地區積澇易發點的積澇風險閾值或一定預警等級的臨界雨量。

3.1 以北京“7·21”特大暴雨為個例的城市水文模型應用及效果檢驗

城市水文模型網格格點數為1 521×1 908，分辨率為30 m，網格左上角經緯度坐標為40.104558°N、116.554678°E。其圖幅范圍覆蓋北京主要城市區域。模型積分的時間步長為2 s。在30 m網格大小情況下，完全能滿足式(17)對水動力模型時間步長的限定。

城市水文模型以2012年7月21日北京地區特大暴雨為個例，用QPE做強迫，模擬地表產流、管網排水量、徑流量、積水淹沒深度及范圍等參量。模型從“7·21”當天的11時模擬到22時。當模擬到21時時，結果顯示整個北京城市區域呈現大面積城市積澇情景(圖4)。此情景與“7·21”當天的實際發生情況幾乎一致。而且積水嚴重地點多集中在道路主干道、道路交叉口及立交橋等地勢低洼處(對照圖4中的積水圖斑)。檢查12個積澇易發點[廣安門、公主墳及西客站隧道等(圖略)]，這些積澇點的平均最大積水深度可達2.22 m左右，與當天的積澇情景吻合。從疊加上地形圖的水淹分布圖(圖略)上也可看到積水區域主要分布在地勢低洼處。這里僅列出廣安門、蓮花橋和六里橋的積水模擬結果及與從網上搜集到的“7·21”的實況災情圖片做對照組合展示，結果顯示水文模型的模擬結果和實際情況比較貼近(圖4)。

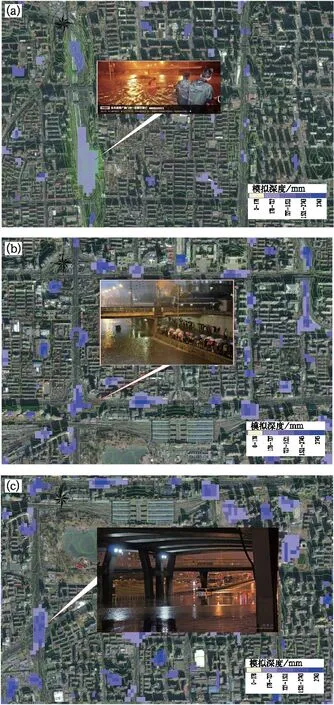
圖4 城市水文模型積分到2012年7月21日21時，北京市廣安門(a),蓮花橋(b)和六里橋(c)的模擬積水深度及對應積水地點的實況情景Fig.4 Simulated inundation mappings and the corresponding observation at (a) Guanganmen， (b) Lianhuaqiao and (c) Liuliqiao overpasses when model integrating to 21:00 BT 21 July 2012

3.2 基于城市水文模型模擬的北京城市積澇易發點暴雨積澇風險閾值搜索及檢驗分析

為找到城市暴雨積澇風險預警的臨界雨量，用城市水文模型脫線模擬的方式搜索臨界雨量。方法用初始的1、3及6 h雨量[比如10 mm·(1 h)-1、10 mm·(3 h)-1及10 mm·(6 h)-1雨量]強迫到城市水文模型，然后強迫雨量值按一定增量(1 mm)遞增，循環模擬及搜索在不同雨量強迫下，城市地區有可能出現0.2、0.5、0.8、1和1.2 m等不同積水深度情況下的臨界雨量值。由于以1 mm為增量遞增，因此雨量分辨率為1 mm。研究統計了不同雨量強迫條件下0.2、0.5、0.8和1.2 m等積水深度的格點面積占總格點面積的占比，其1、3及6 h的模擬結果情況見圖5。研究發現在1 h雨量不大于12 mm，3 h雨量不大于19 mm及6 h雨量不大于31 mm的情況下，研究區圖幅范圍內的積水都沒有大于0.2 m深度的格點。如果以0.2、0.5、0.8和1.2 m 積水深度的格點面積占總格點面積比例剛好達到0.5%作為城市地區積澇災害的藍、黃、橙和紅色預警劃分標準，那么1 h預警等級臨界雨量分別是24、37、45和52 mm，3 h臨界雨量是30、40、48和62 mm，6 h臨界雨量則是39、48、55和69 mm。

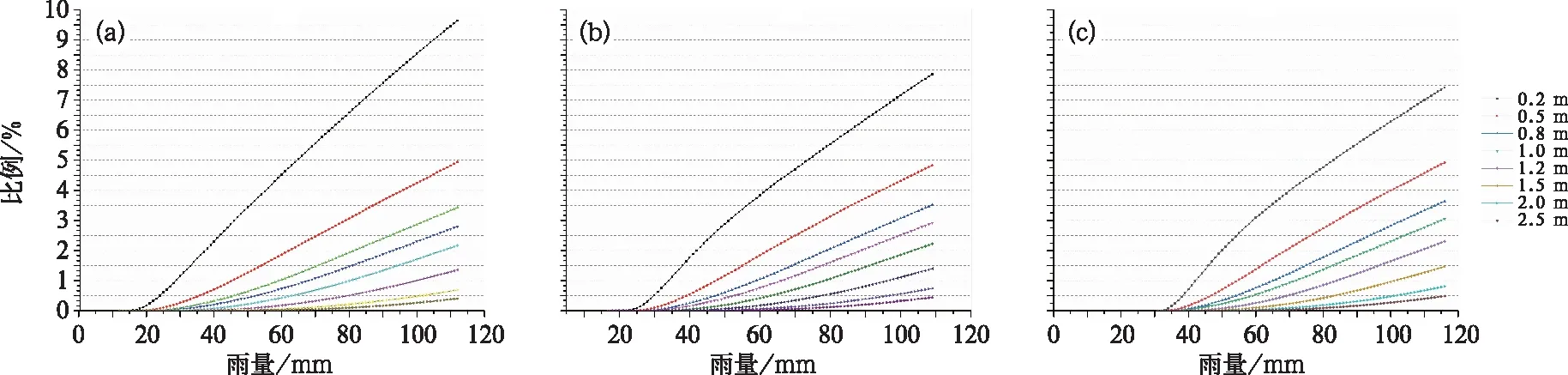
圖5 模型強迫區域范圍內1 h(a)，3 h(b)和6 h(c)雨量遞增情況下一定積水深度格點占總格點比例值的變化Fig.5 Variations of (a) 1 h, (b) 3 h and (c) 6 h accumulated rainfall increments corresponding to the ratios of the cells in inundation depths to the total count of cells, respectively

對照Gourley and Vieux(2005)對GFFG的統計分析可發現紅色預警的1 h臨界雨量超過了美國二千多個流域的1 h的暴雨洪澇風險雨量閾值的眾數(55 mm左右)，而橙色預警的1 h臨界雨量大致在GFFG的中等偏下位置；3 h臨界雨量情況與1 h的類似；而6 h紅色預警臨界雨量值略等于GFFG的眾數值。由于選取的北京城區范圍的不透水地表面積比例較大而且集中，地勢也較為平坦，屬于積澇較敏感地區(扈海波等，2013；尹志聰等，2015)，因此得到這個結果也是可解釋的。

根據2007年北京市防汛辦提供的資料顯示，北京地區積澇易發點共計49個(圖6)，從圖中可發現這些積澇易發點也主要分布在城市交通主干道、道路十字路口及立交橋下。研究在模型模擬結果的圖幅范圍內搜索這些積澇易發點附近0～300 m范圍內，當積水深度超過0.2、0.5、0.8和1.2 m等的臨界雨量值。搜索得到的積澇易發點臨界雨量結果見圖7。這里仍然以積水深度分別超過0.2、0.5、0.8和1.2 m的臨界雨量作為易發點“藍、黃、橙、紅”暴雨積澇風險預警等級指標值。當然，預警指標明確地按分級劃分臨界雨量雖然迎合了確定性預報的要求。但此類指標的不確定性依然存在，例如土地利用及土地覆蓋類型改變、城市排水能力的改進(排水泵的增加及管線的改造)及周邊地形地物的變化等都會導致風險閾值發生改變。因此，風險閾值也需要在水文模型基本參數及輸入更新的情況下，隨時更新及修補。另外，基于臨界雨量的風險預警還應適當運用不確定性的預警及預報方法。Barthold et al(2015)認為用風暴邊緣區域的75%和90%的FFG依然能夠有效識別及預知暴雨積澇。因此在實際應用中還應靈活地參照臨界雨量，考慮不確定性因素，適量滑動臨界雨量取值。

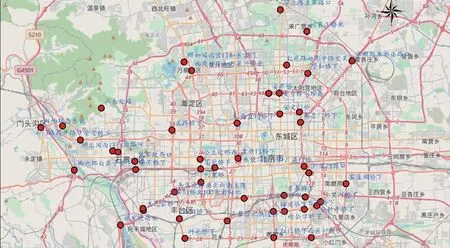
圖6 北京城區積澇易發點分布Fig.6 Distribution of the places susceptible to flash floods in Beijing Metropolis

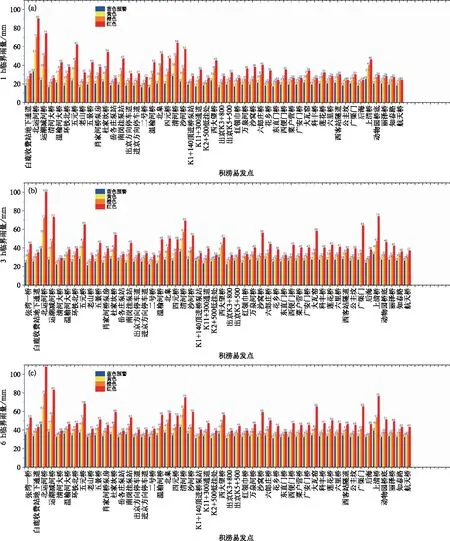
圖7 北京地區49個積澇易發點1 h(a)，3 h(b)，6 h(c)的不同預警等級臨界雨量結果(按照積水深度超越0.2、0.5、0.8及1.2 m核計)Fig.7 The charts of (a) 1 h, (b) 3 h and (c) 6 h cumulative rainfall intensity thresholds for the blue, yellow, orange and red warning signals in 49 places susceptible to flash floods, determined by the inundation depths of 0.2, 0.5, 0.8 and 1.2 m when forcing the rainfall intensity to hydrological model in simulation

城市積澇易發點臨界雨量值開發應用的一個難點是如何有效地檢驗和驗證臨界雨量的有效性及合理性。包括城市水文模型模擬結果的檢驗和驗證一直是個國際難題(Welles et al,2007；Amponsah et al,2016；Sy et al,2020)。Amponsah et al(2016)認為城市積澇事件及其水文過程的對照觀測非常稀少，因為積澇事件的時空尺度很小，在受到此類事件影響的地區缺少相對應的氣象水文觀測，尤其沒有產流強度及水動力過程的觀測，因此針對此類事件的氣象水文觀測驗證是幾乎不可能實現的。Sy et al(2020)則提出通過實地收集和考察來補充及驗證歷史積澇災情信息，認為城市居民對災情的反饋是積澇分析的重要信息源，甚至把由此可獲得的分析結果定義為“市民科學”。因此關于臨界雨量結果的正確性及合理性除了需要與國內外的文獻結果做下縱向的對比外，還需要在實際應用中不斷檢驗和驗證。尤其是“市民科學”的積極參與及投入。

本研究在完成城市積澇易發點不同風險預警等級下的臨界雨量值劃分后，開展對應的應用個例檢驗。這里以2020年7月12日發生在北京南部城區的局地暴雨為例來說明個例在臨界雨量中的檢驗和應用情況(圖8)。該暴雨積澇事件發生在北京市豐臺區南沙窩橋及岳各莊橋一線，從21時左右的該地路面的積澇實情(圖略)來看積水已比較嚴重，積水深度至少在0.5 m左右或以上。對照易發點的暴雨風險預警臨界雨量(圖8a)，20時的RMAPS-in的(圖8b)1 h的QPE達到25 mm左右，這個1 h臨界雨量值對應的預警等級應達到橙色預警程度。如前文所述，即便用QPE做暴雨積澇風險的預警仍然有一定的時間提前量。而從19時起報的QPF來看其1 h雨量為15～20 mm(圖8c)，這個雨量值能對應到藍色及黃色預警等級。可見QPF用來做預警的效果大多受限制于預報結果的準確性，包括落區及雨量準確性。但QPF在預警服務中仍受歡迎，因其具有一定的時間提前量，這個在預警中也是一個關鍵指標，具無法替代的優勢和作用(Silvestro et al,2017；Thorndahl et al,2017；Poletti et al,2019)。

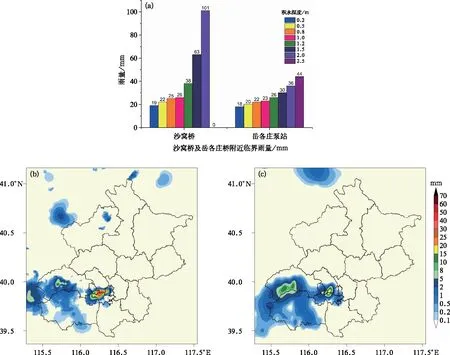
圖8 以2020年7月12日北京市南沙窩橋及岳各莊橋做臨界雨量個例檢驗時，南沙窩橋及岳各莊橋達到不同積水深度所對應的臨界雨量值(a)，20時的1 h的QPE(b)，19時起報的1 h的QPF(c)Fig.8 Illustrative diagrams of the case study on the SFP Nashawoqiao and Yuegezhuangqiao rainfall intensity thresholds validation of their rainfall intensity thresholds corresponding to inundation depths (a), 1 h QPE at 20:00 BT (b), and 1 h QPF initiated at 19:00 BT (c) on 12 July 2020

4 結論與討論

城市暴雨積澇風險預警及預報需要結合氣象及水文兩個領域的相關模型進行交叉應用及開發。本文重點論及城市水文模型基本原理及模型方法實現，以及雷達反演雨量強迫到城市水文模型的積水及積澇情景模擬。然后給出基于城市水文模型的城市暴雨積澇風險預警及預報技術應用。

從模型應用的情況來看，雷達反演雨量的定量降水估計QPE在雨量值及落區準確性上基本能滿足城市水文模型強迫的需求。由于地表產流及徑流生成的延遲效應，一般徑流峰值會落后降水峰值近1 h左右，因此可充分利用這個時間差來發揮QPE在積澇預警中的作用。也就是說結合QPE和臨界雨量值可做暴雨積澇風險預警，其時間提前量可控制在1 h范圍內。而定量降水預報(QPF)的雨量值及落區有較大偏差，尤其是3 h及6 h的預報。此類數據直接強迫到城市水文模型會產生一定的不確定性模擬結果。但是其具相當的時間提前量，同樣是值得積澇預報使用的重要數據，而其1 h預報產品從初步使用的情況來看，基本上還是能根據其雨量場結果做出有效的預警判斷。今后工作中，更應注重結合QPFs及臨界雨量判斷的暴雨積澇預警應用。當然，也更加期待QPFs的1、3及6 h數據準確性和有效性能進一步完善，真正達到城市暴雨積澇預報的要求。

土地利用及土地覆蓋是城市水文模型的重要參數，該參數控制及貫穿應用于城市水文模型的地表水反應過程及水動力過程，因此其數據的準確性及分辨率等均影響模型模擬結果的可靠性。除不透水地表組成是地表產流分析的重要基礎外，地表土地類型屬性及分類更是控制水動力模型參數的基礎，比如水動力模型中的地表粗糙度及產流系數等關鍵參數。此數據的不確定性很大程度制約了水文模型的模擬精度。城市水文模型的高空間分辨率(30 m)特性對土地利用及土地覆蓋的分類結果及精度要求也較高。這類資料最好從高精度的基礎地理信息數據中提取，再輔以高時空分辨率的遙測資料做分類訂正。高分辨率土地利用及土地覆蓋等參數在城市水文模型的模擬分析中的優勢體現在有助于獲得較為準確的地表產流(流量及流速)及匯流，從而能提高模型模擬的整體精確度。

城市水文模型的地表水反應過程的模擬主要在不透水地表及透水地表上展開。在產流估算上，不透水地表的產流損失分量只有少量的洼蓄及蒸發，而透水地表的產流還要持續性減去Hotanian下滲量，因此城市不透水地表面積越大，地表產流越多，積澇風險就越大。另外，用路網GIS資料間接推算的城市管網的排水能力可參數化到城市水文模型中，其導致模擬的不確定性及有效性需要進一步評測，但這種參數化方案在計算資源分配及可參數化應用上有一定的優勢。提取到的城市排水能力參數分布表明城區的管網排水能力大于近郊區，但不透水面積比例較大，因此反而更容易發生積澇事件。

需要特別提及的是在徑流路徑尋徑上，城市地區的地表建筑物等相關阻礙物較多，地表徑流的紊流、分流及散流情況也多，因此建議城市水文模型的徑流路徑尋向用多流向算法或通過與多流向算法效果類似的回水機制來實現。

城市水動力模型可建立在基于積水深度均勻的二維淺水方程上。淺水假定消除了局地加速、對流加速及對流壓力項，但其對模擬精度的影響不大，甚至遠低于地形參數和地表粗糙度等邊界條件不確定性對模擬精度的影響。淺水下的低速緩流狀態完全符合城市地表徑流及積水匯流的水動力情況。淺水假定還便于城市水動力方程的求解。本文提出借用ADI分兩步求解水動力模型的差分方程。而且水動力模型差分方程的求解包含了回水機制，同時對模型的時間步長做了規約，確保模型格點單元的水量連續性及均衡性(Hodges,2019)。需要注意的是盡管Thomas算法只是個小的計算技巧，該算法卻是求解差分方程的關鍵。

本文論及的暴雨積澇風險預警及預報模式主要有在線及脫線運行兩種方式。從實例應用及分析來看，北京“7·21”特大暴雨個例的實況雷達反演雨量強迫到水文模型，大體能模擬到當天的積澇情景。盡管用城市水文模型實時模擬積水狀況并用模擬結果實施暴雨積澇風險預警在技術上可行，但水文模型在線方式在氣象業務運行過程中會因模型模擬參數讀取及結果解讀的繁雜處理流程、較高的數據處理及計算量、結果的不確定性、模型運用的熟練度及運用技巧限制等缺陷而使得其應用前景并非看上去那么美好。因此，本文提出參照NWS的FGGs的脫線模式不失為一種更為合理的城市暴雨積澇預警及預報模式。基于城市水文模型的脫線運行方式把積澇易發點對應一定積水深度的臨界雨量模擬輸出，此臨界雨量可作為預報員在做暴雨預警時的重要參考，方便預報員直觀做出合理的預警判斷及發布。研究以0.2、0.5、0.8和1.2 m積水深度的格點面積占總格點面積比例達到0.5%作為城市地區積澇災害的藍、黃、橙及紅色預警劃分標準，得出北京地區1 h的對應預警等級的臨界雨量分別為24、37、45和52 mm；3 h臨界雨量則分別為30、40、48和62 mm，6 h分別為39、48、55和69 mm。然后，用城市水文模型模擬出了北京地區至少49個積澇易發點在積水深度達到0.2、0.5、0.8和1.2 m時的1、3和6 h的臨界雨量，并以這些臨界雨量作為積澇易發點暴雨積澇的“藍、黃、橙、紅”預警等級判斷及實時監控標準。通過與國內外文獻資料的對比分析及個別積澇個例的初步檢驗，基本可認為這些臨界雨量及對應的預警等級標準有一定的可信度及合理性。

附錄：

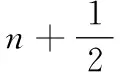
(1)

其中：

第二步在y方向上的顯式(explicit)計算式如下,同樣可組合為線性方程組:

(2)