繩驅動連續體機器人標定方法

李法民 鄭天江 沈雯鈞 王會肖 方灶軍 梁冬泰

1.寧波大學機械工程與力學學院，寧波，3152112.中國科學院寧波材料技術與工程研究所,寧波，3152013.浙江省機器人與智能制造裝備技術重點實驗室,寧波，315201

0 引言

與傳統工業機器人相比，連續體機器人具有柔順性高、能夠實現連續變形等特點，越來越受到國內外學者的關注。

學者針對不同的應用場景提出了多種連續體機器人構型。KANG等[1]提出了一種將肌腱嵌入氣動肌肉的連續體機器人，并建立了機器人的三維動力學模型。ZHANG等[2]以形狀記憶合金(SMA)作為驅動模塊，搭建了具有4個關節模塊的模塊化機器人臂，根據SMA的特點建立了自反饋控制系統，實現了機器人的控制。OTAKE等[3]研究了基于電活性聚合物凝膠的軟連續體機器人，提出了電活性聚合物系統的動力學模型，并通過施加空間或時變電場來實現各種運動。周圓圓等[4]提出了一種新構型的6自由度連續體手術機器人，其形變骨架采用超彈性材料一體化成形加工，形成具有一系列十字交叉鏤空結構的彈性鉸鏈。MANTI等[5]提出了一種繩驅動連續體機械臂，該機械臂將驅動繩索與彈性流體制動器相結合，能夠實現彎曲、拉伸和收縮運動。與其他連續體機器人構型相比，采用繩索驅動的連續體機器人通過繩索來傳力，其傳動裝置可以安裝于基座，這有利于實現機器人運動部件的輕量化，且繩驅動機器人的帶載荷能力較大，因此，該構型適用于復雜環境內運動及本質安全的人機交互，被廣泛應用在狹窄空間檢測[6]、輕量化機械臂[7]、外科手術[8]等領域。

由于連續體機器人容易產生柔性變形，故其控制精度較傳統機器人更容易受加工、安裝以及外載荷等因素影響。與傳統機器人相比，繩驅動連續體機器人更需要通過標定來提高其精度。

國內外學者針對傳統工業機器人的標定做了大量研究。YANG等[9]針對并聯機器人提出了標定方法，該方法將旋量、關節角誤差都歸納到初始位姿的誤差中，誤差模型簡單。谷樂豐等[10]提出了一種由安裝于機器人末端球心位置的測量裝置和可移動球桿組成的新型便攜式機器人標定裝置，能夠在較大空間中進行標定。KURBANHUSEN等[11]針對剛性關節繩驅動機器人標定方法進行了研究。CHEN等[12]針對7自由度繩驅動剛性機械臂，提出了一種集成化的兩級自校準方法。雖然學者提出了大量的標定方法，但一般需在機器人末端安裝測量裝置，這使得多數方法不能直接用于易產生柔性變形的連續體機器人，且目前針對連續體機器人的標定方法研究較少。

本文設計了一種基于柔性支撐構型的繩驅動連續體機器人關節模塊，該關節模塊以柔性液壓軟管材料作為支撐骨架，通過4根繩索牽引，可實現2-DOF的連續彎曲運動。為提高定位精度，本文利用指數積(POE)公式建立了基于柔性支撐構型的繩驅動連續體機器人關節模塊的運動學模型，然后推導出了基于運動學的誤差傳遞模型。

1 基于柔性支撐的繩驅動關節模塊設計

基于柔性支撐的繩驅動連續體機器人關節模塊模型見圖1。關節模塊由基座、動平臺、柔性支撐骨架及4根驅動繩索連接構成。為簡化設計，動平臺與基座具有相同結構。柔性支撐骨架采用液壓軟管材料，具有較高的抗拉壓和扭轉剛度，能夠大幅減少運動過程中產生的拉伸、壓縮、扭轉等復雜變形。驅動繩索為剛閘繩，繩的連接點均勻分布在動平臺與基座上，通過驅動電機牽引繩索，可實現單關節模塊的兩自由度彎曲運動。

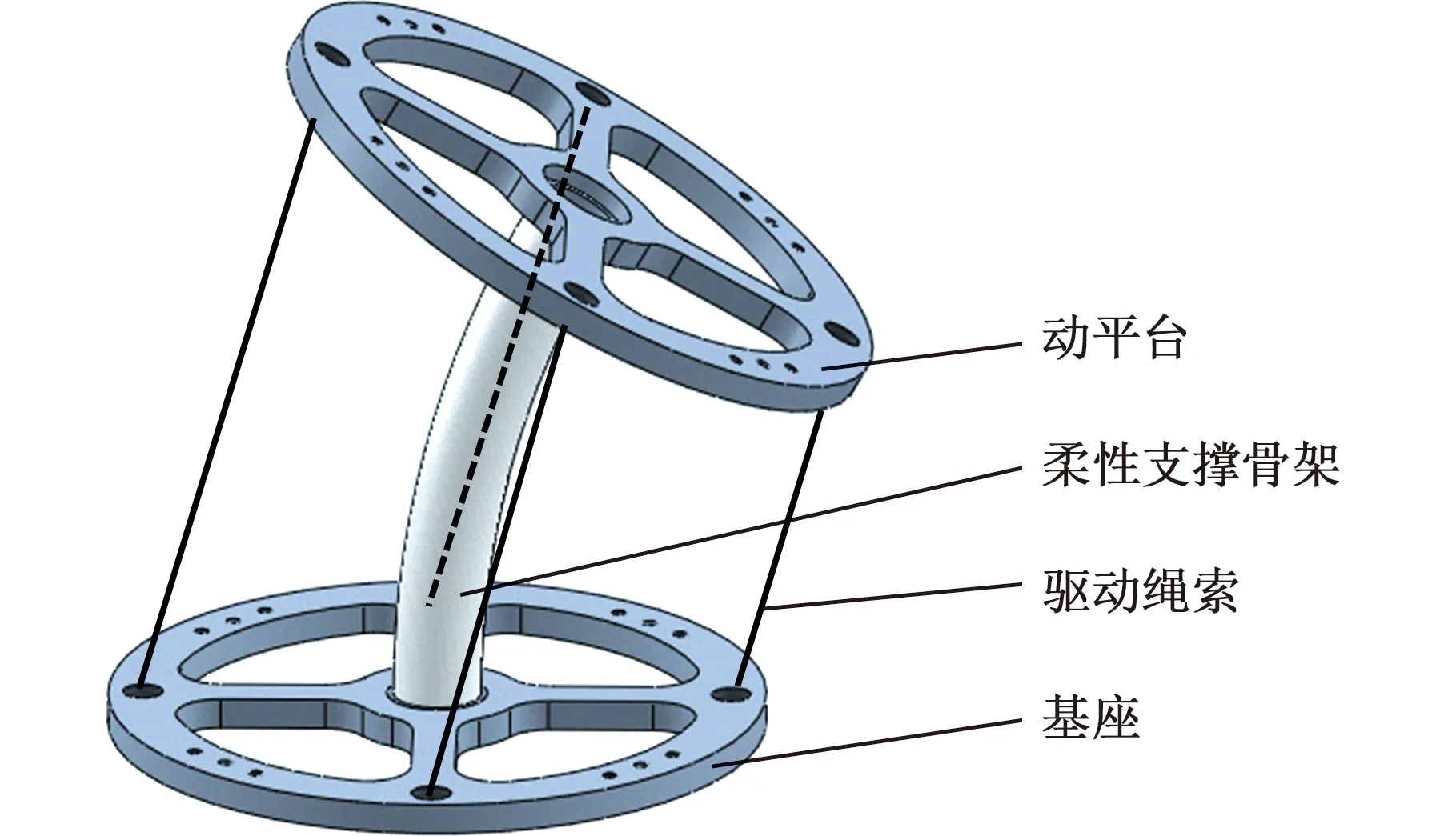
圖1 繩驅動單關節模塊模型Fig.1 Model of cable-driven segment

2 繩驅動連續體機器人運動學分析

2.1 單關節模塊運動學分析

繩驅動單關節模塊運動學簡化模型如圖2所示，點OB、OM分別為基座、動平臺的圓心，Bi、Mi(i=1,2,3,4)為4根繩索連接點。在基座、動平臺上分別建立坐標系OBXBYBZB、OMXMYMZM，兩坐標系分別以OB、OM為原點，以OB、OM指向第一根繩索連接點的方向為軸XB、XM，以垂直于基座、動平臺的方向為軸ZB、ZM。由于4根繩索均勻分布在平臺上，所以軸YB、YM分別指向平臺第二根繩索連接點。

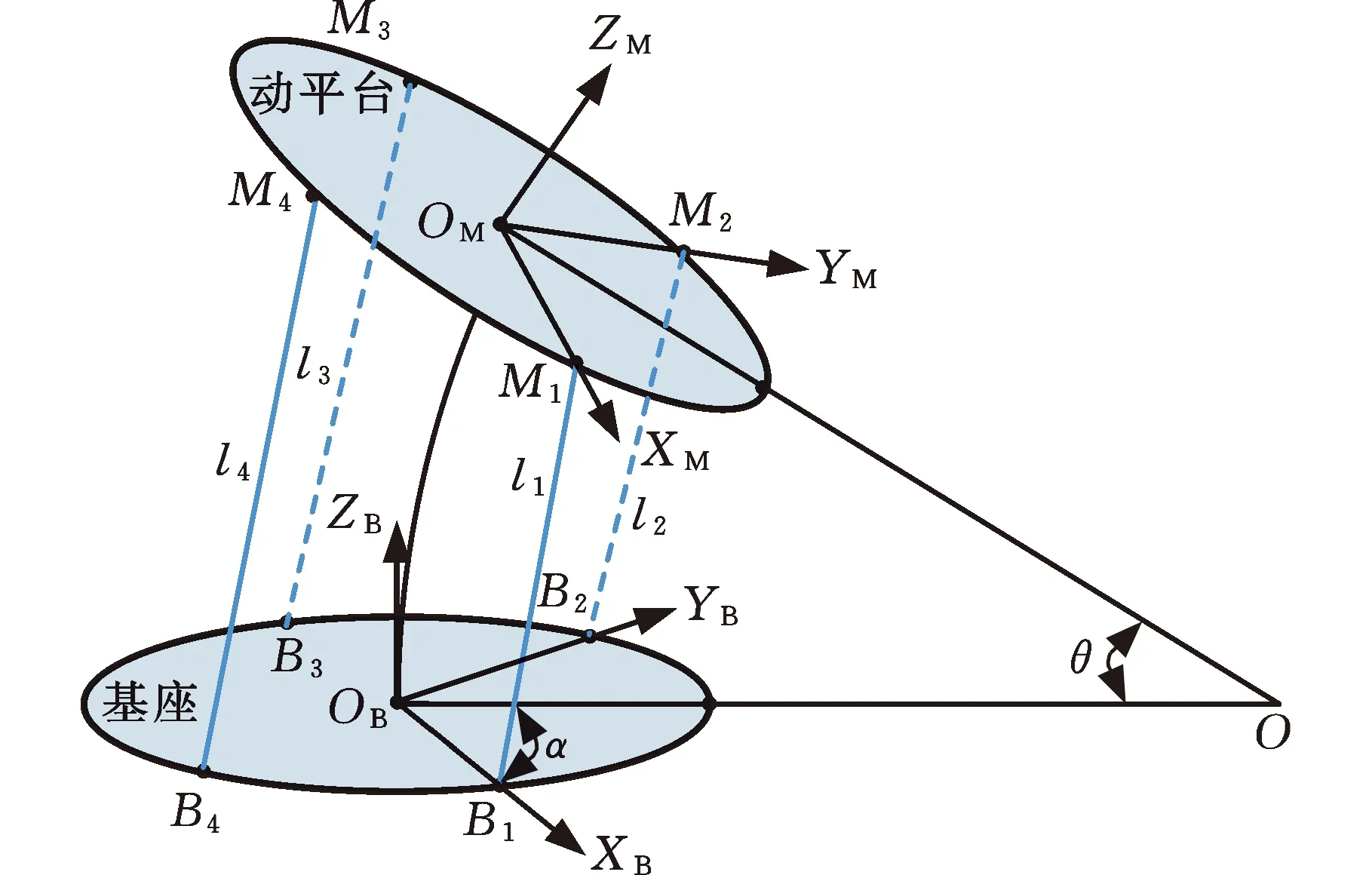
圖2 單關節模塊運動學模型Fig.2 Kinematics model of segment

假定柔性支撐骨架的彎曲形變理想化，則OBOM為一條定長為l的圓弧。平面OBOMO由軸ZB、ZM以及圓弧OBOM組成，分別交基座、動平臺于直線OBO、OMO，且OBO與OMO相交于O點，該平面始終垂直于基座。

定義關節變量旋轉角α和彎曲角θ，通過兩關節變量α、θ來描述單關節模塊的彎曲運動。其中，α為軸XB與直線OBO的夾角，表示關節彎曲的方向；θ為∠OMOOB，表示關節彎曲的角度。

2.1.1關節變量與動平臺末端位姿運動學分析

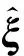
(1)

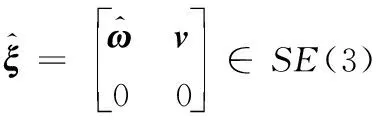
ξ=(v,ω)∈R6×1

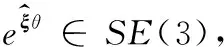
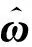
根據正向運動學變換關系，T(α,θ)可表示為

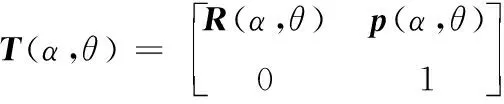
(2)

式中，R(α,θ)∈SO(3),為坐標系OMXMYMZM相對于OBXBYBZB的方向；p(α,θ)為坐標系OMXMYMZM相對于OBXBYBZB的位置向量。

由式(1)可得

(3)

(4)

由式(3)、式(4)可得

(5)

(6)

式中，L為柔性骨架的長度。

綜上所述，若給定關節變量α、θ，則繩驅動關節模塊的動平臺相對于基座的位姿也確定。

2.1.2關節變量與繩長的運動學分析

‖BiMi‖表示第i根繩索的長度，根據幾何關系，有

BiMi=BiOB+OBOM+OMMi

(7)

則第i根繩索的表達式為

(8)

(9)

式中，βi為OBO與OBBi的夾角；r為繩連接點所在圓的半徑。

由式(8)可得繩長與關節角的數學關系：

(10)

(11)

2.2 連續體機器人運動學分析

繩驅動連續體機器人是由多個相同的2-DOF繩驅動單關節模塊連接構成。對于n個單關節模塊組成的連續體機器人，其正向運動學模型為

T0,n=T0,1(α1,θ1)…Ti-1,i(αi,θi)…Tn-1,n(αn,θn)

(12)

式中，Ti-1,i(αi,θi)為第i個關節的運動學模型。

給定每個單關節模塊的旋轉角α、彎曲角θ，則繩驅動連續體機器人的末端動平臺相對于基座系的位姿便可確定。

3 繩驅動連續體機器人標定算法

3.1 誤差模型

對于由n個關節模塊構成的繩驅動連續體機器人，由式(12)可知，其運動學模型是關于初始位姿T(0)、旋量ξ、關節角q的函數，即

T=f(T(0),ξ,q)

(13)

T(0)=[T0,1(0)T1,2(0) …Tn-1,n(0)]T

ξ=[ξ1ξ2…ξn]T

q=[q1q2…qn]T

對式(13)進行微分，有

(14)

由式(14)可知，末端位姿誤差δT·T-1由δT(0)、δξ和δq三個參數決定。由于ξ是關節角q=[αθ]T的函數，這里暫時不考慮旋量帶來的誤差，故只需推導出最終與δT(0)和δq相關的末端誤差模型。式(14)可簡化為

(15)

對式(12)進行微分，可得

(16)

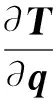
(17)

δti=[dxidyidziδxiδyiδzi]

Ji4=ωδqi=[δαiδθi]T

式中，Ad(T)表示求矩陣T的伴隨變換矩陣，δti為第i個關節末端運動學誤差；Ji為第i個關節的雅可比矩陣[14]；δqi為第i個關節的角度誤差；ω′為ω的導數。

根據李群李代數相關理論[13]，可得

(18)

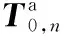
將式(16)～式(18)代入式(15)，得

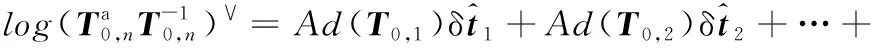
(19)

將式(19)線性化表示為

y=Ax

(20)

其中，y為末端位姿誤差，x為機器人的運動學誤差，具體表達式為

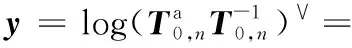
Ad(Tq)=[Ad(T0,1(0))J1Ad(T0,1)Ad(T1,2(0))J2

…Ad(T0,n-1)Ad(Tn-1,n(0))Jn]
δt=[δt1δt2…δtn]T
δq=[δq1δq2… δqn]T

若測量m組數據，則式(20)可擴展為

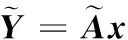
(21)

由式(21)得

(22)

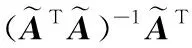
3.2 模型參數的最小二乘法求解

為得到高精度的運動學模型參數，采用最小二乘法對式(22)進行迭代計算，算法流程如圖3所示。

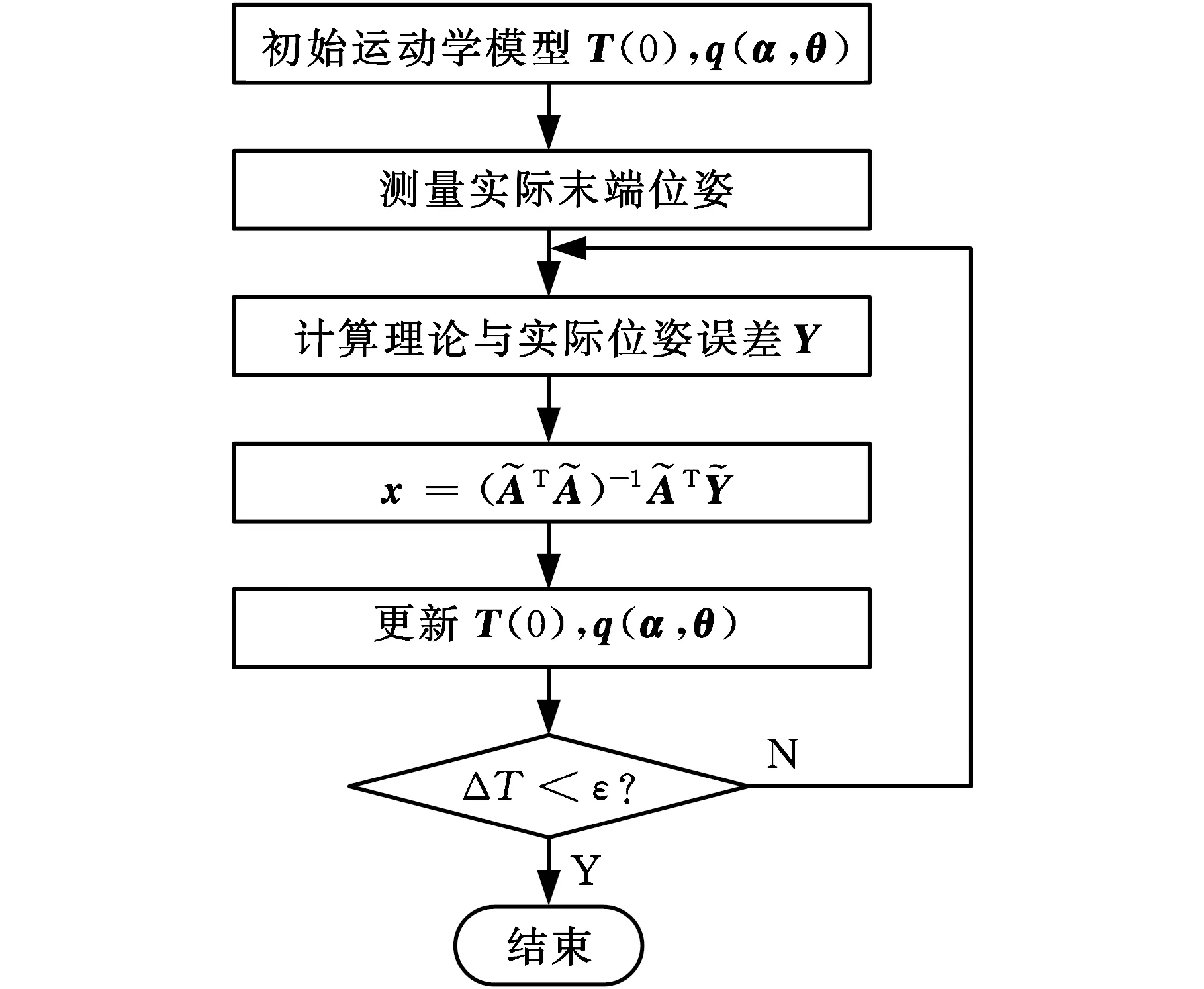
圖3 標定算法流程圖Fig.3 Flow chart of the calibration algorithm

4 仿真分析

4.1 仿真過程

本文利用MATLAB作為計算工具，對上述繩驅動連續體機器人進行仿真驗證。

選擇的仿真模型為繩驅動連續體機器人單關節模塊，其主要模型參數為：柔性支撐長度L=120 mm，繩索連接點到平臺圓心距離r=67 mm，初始位姿矩陣為

對運動學初始參數T0,1(0)、ξ、q分別預設誤差Δt、Δξ、Δq，其中:

Δt=[0 0.1 mm 0.1 mm -0.1 mm 0 0]T

Δξ=[0.02 0 0 0 sin 0.02 cos 0.02-1]

Δq=[0.008° 0.008°]T

則實際模型參數表示為

ξa=ξ+Δξqa=q+Δq

此時，繩驅動單關節模塊的運動學模型為

(23)

4.2 仿真結果分析

仿真導入30組關節角，其中前20組用于迭代求解標定后的運動學參數，后10組用于驗證標定后運動學參數的正確性。

定義平均位置誤差Ep和平均姿態誤差Eo，具體表示為

圖4所示為前20組數據的平均誤差隨迭代次數收斂情況。位置誤差經6次迭代，從11.727 mm下降到0.0978 mm，姿態誤差從0.0929 rad下降到0.0027 rad，且第二次迭代時位置誤差就已下降到1.043 mm，姿態誤差下降到0.0068 rad，說明算法具有較好的收斂性。

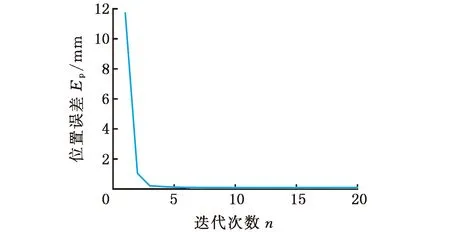
(a)位置誤差迭代過程

通過標定算法得到新的運動學模型參數：

利用后10組數據對標定后的運動學模型進行驗證，結果如圖5所示。10組數據的平均位置誤差為0.109 mm，平均姿態誤差為0.0029 rad，驗證了標定算法的可行性。

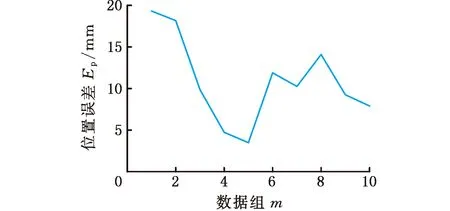
(a)位置誤差

4.3 算法對比

傳統工業機器人標定方法一般僅考慮初始位姿誤差對精度的影響，如文獻[9]針對并聯機器人提出的標定算法。本文對文獻[9]的傳統工業機器人標定算法進行仿真計算，并將其結果與本文所提算法進行比較，對比結果如圖6所示。

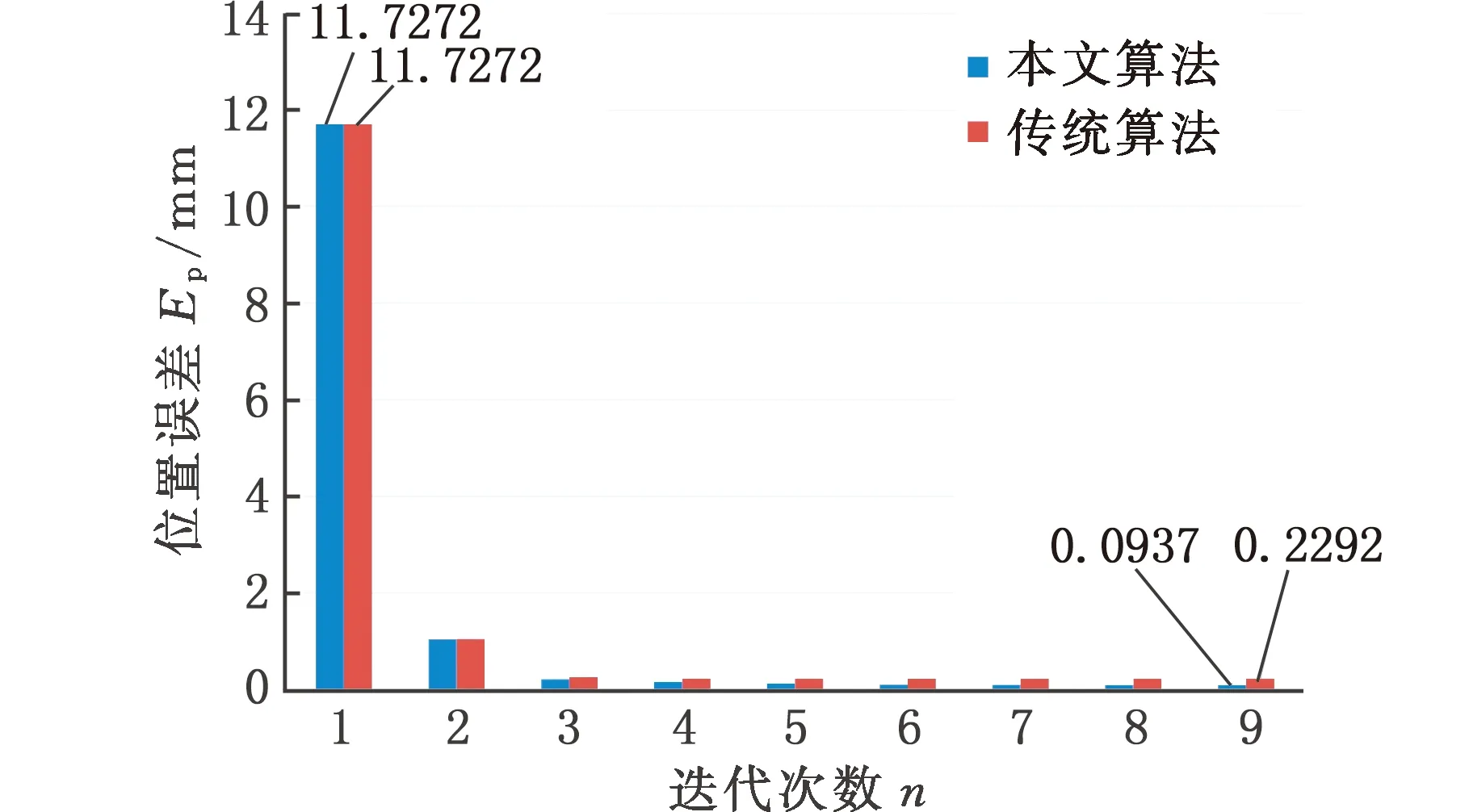
(a)位置誤差對比

由圖6可得，傳統算法經迭代后位置誤差下降到0.2292 mm，姿態誤差下降到0.0041 rad。根據仿真結果對比可得，本文所提算法能夠獲得更小的收斂誤差，得到的運動學模型精度相對較高，這進一步驗證所提算法的可行性。

5 實驗驗證

為驗證標定算法的有效性，利用繩驅動單關節模塊樣機進行了實驗。實驗環境布置如圖7所示，實驗設備由運動捕捉系統(qualisys track manager，QTM)、上位機、繩驅動樣機、驅動電機組成，其中運動捕捉系統測量關節末端位姿，上位機用于控制繩驅動單關節模塊，驅動電機牽引繩索運動。如圖8所示，樣機采用4根繩索驅動，柔性支撐的長度L=120 mm，繩索連接點所在圓周的半徑r=67 mm。

圖7 實驗裝置Fig.7 Experimental equipment

圖8 繩驅動單關節樣機Fig.8 Prototype of cable-drive segment

5.1 實驗步驟

實驗中，在基座、動平臺上放置標記小球(3個)，通過QTM測得標記小球的坐標。根據3個小球坐標分別計算基座、末端動平臺在QTM坐標系下的位姿TQ,B、TQ,E，則可得到末端在基座坐標系下的實際位姿TB,E：

(24)

實驗具體步驟如下：

(1)運用QTM測量基于初始運動學模型的120組數據，其中前80組通過標定算法計算新的理論模型參數，后40組計算位姿誤差用于數據對比；

(2)將步驟(1)中計算出的標定后的模型參數重新導入上位機；

(3)測量基于標定后運動學模型的40組數據(與步驟(1)中40組關節角相同)，計算末端位姿誤差；

(4)比較步驟(1)、步驟(3)中40組數據的末端位姿誤差，驗證算法有效性。

5.2 實驗數據分析

實驗步驟(1)中80組數據迭代的收斂性如圖9所示，通過4次迭代初始位置誤差從3.836 mm下降到1.153 mm，姿態誤差從0.123 rad下降到0.022 rad，算法的收斂性較好。

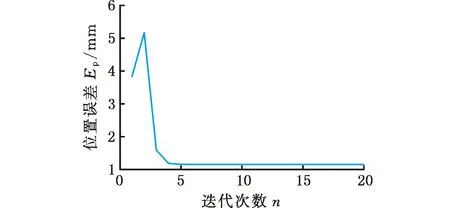
(a)位置誤差

標定算法最終得到的新運動學參數為

將標定后的新運動學模型導入上位機，采集實驗步驟(3)中40組數據，將該數據與實驗步驟(1)中40組數據進行對比，結果如圖10所示。標定前位置平均誤差為3.955 mm，姿態平均誤差為0.122 rad。標定后位置平均誤差為2.68 mm，姿態平均誤差為0.0224 rad。

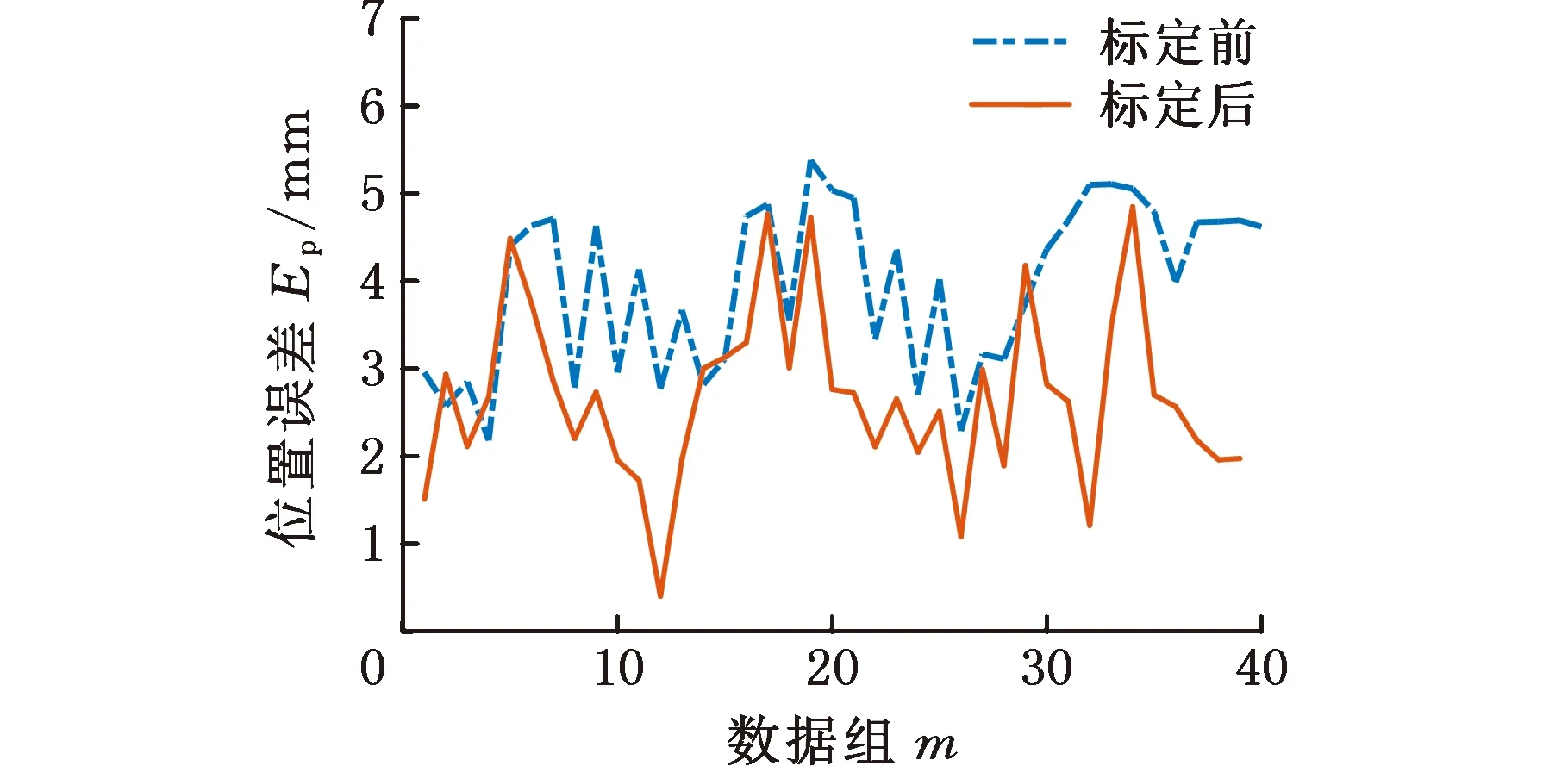
(a)位置誤差

5.3 實驗結果分析

根據實驗數據分析可得：繩驅動連續體單關節模塊位置平均誤差從標定前的3.955 mm下降到2.68 mm，位置精度提高了32.23%；平均姿態誤差從0.122 rad下降到0.0224 rad，姿態精度提高了81.64%，證明了標定算法的有效性。

根據實驗數據，繩驅動單關節樣機在標定后位置、姿態仍存在一定誤差。繩驅動連續體機器人為弱剛度系統，自重是導致機器人存在誤差重要原因之一。另外，驅動繩索在運動過程中存在的摩擦力也會影響機器人控制精度。

6 結束語

提出了基于柔性支撐的繩驅動連續體機器人構型，根據指數積公式建立了機器人的運動學模型。針對機器人控制精度較差的問題，提出了誤差標定算法，通過標定算法計算出準確的運動學模型。仿真結果顯示，該算法能夠快速收斂，并正確得到標定后的運動學參數，證明了該標定算法的可行性。最后，制作了繩驅動連續體機器人單關節樣機，對誤差標定算法進行了驗證。實驗結果顯示，機器人末端位置精度提高了32.23%，姿態精度提高了81.64%，驗證了標定算法的有效性。未來，將針對自重和摩擦等非幾何因素導致的誤差問題進行研究，進一步提高繩驅動連續體機器人的控制精度。