基于GPU并行的二維時空中子動力學MOC程序開發及驗證

鄒 航，梁 亮，張 乾,*，宋佩濤，趙 強

(1.哈爾濱工程大學 核安全與仿真技術國防重點學科實驗室，黑龍江 哈爾濱 150001；2.西安核創能源科技有限公司，陜西 西安 710077；3.中國輻射防護研究院，山西 太原 030006)

為解決中子在不均勻介質中的輸運問題，特征線方法(MOC)以其幾何普適性的優點，成為近年來反應堆物理設計分析的研究熱點。為提高三維非均勻全堆芯輸運計算效率，國際上提出2D/1D耦合方法來加速計算[1-3]，其中高效率的2D-MOC求解器在全堆輸運計算中占有重要地位。由于MOC方法本身具有計算量大、收斂較慢的不足之處，且在中子動力學計算中變得尤為明顯，因此國內外提出了一系列加速收斂方法在數值層面上提高MOC的動力學計算效率。其中，粗網有限差分方法(CMFD)能顯著降低每個時間步輸運計算的迭代次數，但由于動力學問題本身收斂較慢，美國密歇根大學提出多級瞬態方法(TML)并應用在MPACT上[2,4]，TML采用預估矯正準靜態(PCQS)的思想，將點堆中子動力學、CMFD以及輸運計算相耦合，使得在大時間步長條件下能獲得較高計算精度，且在CMFD計算中使用1G-CMFD加速MG-CMFD收斂[5]。西安交通大學使用簡化源縮放法(SSSM)解決CMFD固定源計算中通量幅值與形狀收斂速度不匹配的問題，并在PCQS中點堆中子動力學部分使用在線高階拉格朗日插值來獲得更高精度的反應性計算值[6]。隨著圖形處理器(GPU)在算力、功耗方面的快速發展，針對GPU自身硬件特性而開發的并行算法已經被大量應用于科學計算領域。MOC方法具有天然并行特性，國內外已開展了基于GPU加速MOC計算的相關研究[7-14]。本文針對全隱式差分方法，同時采用CUDA編程和CMFD加速技術，實現基于GPU并行的二維MOC瞬態計算。

1 中子輸運動力學計算理論

1.1 中子輸運動力學方程

求解中子輸運動力學方程的核心思想是對其進行時間差分[3]，并利用先驅核方程積分方法將先驅核方程與中子輸運方程進行耦合，推導得到一系列與穩態方程形式相當的瞬態固定源方程(TFSP)，并利用穩態中子輸運方程求解方法對其進行逐時間步求解。中子輸運方程和先驅核方程如式(1)與式(2)所示：

χp,g(r,t)(1-β(r,t))SF(r,t)+Sd,g(r,t))

(1)

k=1,2,…,6

(2)

式中：vg為能群g下的中子速度；φg為位置r處方向為Ω的中子角通量密度；Ck為緩發中子先驅核濃度；Σt,g為宏觀總截面；βk為緩發中子份額；λk為衰變常量；Ss,g為散射源項；SF為裂變源項；Sd,g為緩發中子源項；χp,g為瞬發中子裂變譜。各源項定義如式(3)～(6)所示。

(3)

(4)

(5)

(6)

對式(1)的時間項進行全隱式差分，可得式(7)：

(7)

(8)

(9)

(10)

(11)

(12)

(13)

1.2 CMFD加速

多群CMFD TFSP方程可由中子擴散動力學方程[2,4-5]推導得出，格式如下：

(14)

(15)

對式(14)使用與推導輸運動力學方程相同的時間差分方法，可得式(16)：

(16)

(17)

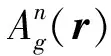
(18)

(19)

(20)

Str=AΦ+BFΦ+C

(21)

將各算子代入式(16)可得CMFD TFSP方程：

(M-S)Φ=χFΦ+AΦ+BFΦ+C

(22)

1.3 MOC動力學計算

由1.1節可知，2D MOC動力學方程可寫為如下形式[2,4,6]：

(23)

其中瞬態固定源項定義與式(9)相同：

(24)

在原有源項上加上瞬態固定源項后，式(24)可由穩態MOC求解器逐時間步求解，且現有的并行加速算法不需作較大改動即可套用至動力學計算上。

2 并行算法設計及程序開發

本文基于上述理論，以現有的柵格物理程序ALPHA穩態版本為基礎，調用其MOC求解器及CMFD求解器來開發其動力學計算功能。ALPHA中采用GPU加速CMFD及MOC計算，MOC計算中采用特征線-單能群并行策略，CMFD計算采用紅-黑排序并行求解策略[6-12]，具體計算流程如圖1所示。

圖1 GPU加速的MOC耦合CMFD求解瞬態固定源問題流程圖Fig.1 TFSP solution procedure for MOC with CMFD acceleration based on GPU

整體計算流程如下：1) 在CPU端進行初始穩態和動力學的初始化計算，包括幾何預處理和截面初始化等計算所需信息；2) 將幾何、截面信息從系統內存一次性拷貝到顯存；3) 執行CMFD計算，為MOC迭代提供初值；4) 通過本征值和通量偏差判斷整體迭代是否收斂。

CMFD計算主要包括：1) 粗網多群參數歸并及線性系統的構造，由于各粗網參數和CMFD方程組中各方程相互獨立，可將粗網參數歸并與方程構造分配給各GPU線程并行執行；2) CMFD源項更新也可在GPU端并行執行，每個線程負責單個粗網單個能群的源項計算；3) CMFD線性系統求解，本文所采用的線性方程組解法為逐次超松弛迭代(SOR)，為保證在GPU并行求解，本文采用紅-黑排序，將相互獨立的方程求解分配給不同的GPU線程并行執行，因此求解過程中有1/2的方程可并行求解，隨后提供更新后的結果，用于另一半方程的并行求解；4) CMFD收斂后，利用CMFD結果更新MOC細網通量，為下一次MOC計算提供初值。采用GPU線程并行后，1個線程執行1個粗網內所有細網在單個能群下的通量更新。

MOC將采用CMFD更新后的通量進行計算。本文采用Jacobi格式的輸運掃描算法進行輸運求解，其中源項計算采用GPU多線程并行求解，輸運掃描計算采用的特征線-能群并行的策略。

3 數值驗證

本文采用TWIGL基準題與2D MINI-CORE基準題測試程序精度及效率。計算平臺采用多核工作站，工作站所用CPU為Intel Core i7-8700K，所用GPU為NVIDIA Geforce 2080Ti。

3.1 TWIGL基準題

TWIGL基準題[15]是一個兩群三區問題，其幾何結構及堆芯網格劃分如圖2所示。TWIGL堆芯內部由3種不同材料區域構成，通過改變區域1材料的熱吸收截面來驅動堆芯功率發生瞬態變化。ALPHA的計算參數如下：柵元尺寸2.0 cm×2.0 cm，每個柵元使用5×5矩形網格劃分，特征線間距0.02 cm，角度離散采用32個輻角和最佳三極角，初始穩態和動力學計算通量收斂準則均為1.0×10-7，時間步長分別選用2、5和10 ms，CPU和GPU計算均使用雙精度。

圖2 TWIGL基準題幾何結構及堆芯網格劃分Fig.2 TWIGL benchmark geometry and core division strategy

堆芯功率時變計算結果如圖3、4所示，參考解由VARIANT和DeCART給出[15]，可看出ALPHA計算結果與參考解符合良好，堆芯功率最大相對誤差為0.43%。各區域平均棒功率計算結果比較列于表1。區域3功率相對誤差較區域1、2大，最大誤差出現在0.2 s，恰好是功率開始瞬變的時刻。帶有CMFD加速的不同硬件條件下計算效率與精度比較列于表2。由于TWIGL問題規模較小，GPU算例中對于每個時間步的計算時間并不能達到所用GPU的峰值算力，且調用GPU過程中所消耗計算資源占比較多，所以GPU算例計算時間并未隨著步長增大而呈比例地減小，但相比CPU算例而言，加速效果依然明顯。對于2 ms步長算例，加速比達到6.6。GPU并行條件下的CMFD加速效率對比列于表3。CMFD加速性能十分可觀，加速比基本在40左右。對比表3中3種不同的時間步長計算結果可發現，CMFD時間占比隨時間步長的減小而減小，從而CMFD加速比也隨之減小。對比表2與表3結果可發現，GPU并行條件下的加速比隨著MOC計算時間占比增大而增大。

圖3 TWIGL功率變化及相對誤差Fig.3 Core power behavior of TWIGL and relative error

圖4 不同時刻TWIGL精細功率分布 Fig.4 Detailed power distribution of TWIGL at different time

表1 TWIGL各區域平均棒功率計算結果比較Table 1 Region wise pin power comparison of TWIGL

表2 TWIGL基準題不同硬件條件下計算效率及精度比較Table 2 Computational efficiency and accuracy comparison for TWIGL in different hardware conditions

表3 TWIGL基準題CMFD加速效率比較Table 3 Effectiveness of CMFD for TWIGL

3.2 MINI-CORE 2D基準題

MINI-CORE 2D基準題[15]幾何結構以及邊界條件如圖5所示，該堆芯由5個鈾富集度為4.2%的UOX組件和4個钚富集度為4.0%的MOX組件組成。控制棒僅位于中心的UOX組件內，通過勻速提棒使得堆芯產生瞬態功率變化。ALPHA的計算參數如下：每個組件為17×17柵元排布，每個柵元使用5×5矩形網格劃分，選用特征線間距為0.02 cm，角度離散選用32輻角和最佳三極角，初始穩態和動力學計算通量收斂準則均為1.0×10-6，CPU和GPU計算均使用雙精度。

圖5 MINI-CORE 2D基準題幾何結構Fig.5 MINI-CORE 2D benchmark geometry

堆芯功率時變計算結果如圖6、7所示，參考解由DeCART與VARIANT給出[15]，ALPHA計算結果與參考解符合良好，2 ms步長算例中堆芯功率最大相對誤差為3.3%，出現位置在0.01 s。不同時刻下組件功率計算結果列于表4，各時刻下組件功率相對誤差均在0.05%以內。帶有CMFD加速的不同硬件條件下計算效率與精度比較列于表5，可看出GPU計算加速效果良好，對于2 ms算例加速比為3.8倍。GPU條件下的CMFD加速效率對比列于表6，CMFD加速效果明顯，10 ms算例加速比可達到51.6。MINI-CORE基準題中GPU加速比與CMFD時間占比的關系與TWIGL結果一致，即GPU加速比隨CMFD時間占比增大而減小。

圖6 MINI-CORE 2D功率變化及相對誤差Fig.6 Core power behavior of MINI-CORE 2D and relative error

圖7 不同時刻MINI-CORE 2D精細功率分布 Fig.7 Detailed power distribution of MINI-CORE 2D at different time

表4 MINI-CORE 2D各區域平均棒功率計算結果比較Table 4 Region wise pin power comparison of MINI-CORE 2D

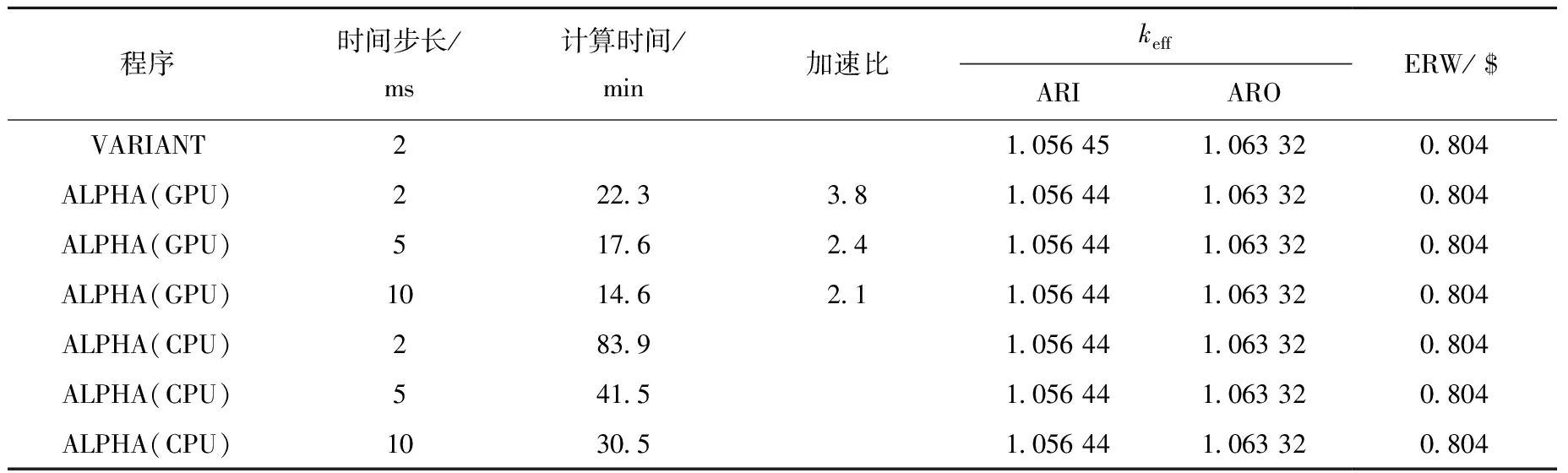
表5 MINI-CORE 2D基準題keff及計算效率比較Table 5 Steady-state keff and calculation efficiency of MINI-CORE 2D

表6 MINI-CORE基準題CMFD加速效率比較Table 6 Effectiveness of CMFD for MINI-CORE

4 結論

本文介紹了采用GPU加速的TFSP并行算法，實現了GPU并行加速動力學MOC及CMFD計算。TWIGL基準題和MINI-CORE 2D基準題數值結果表明：程序滿足瞬態輸運求解的精度要求；同時，采用單GPU進行小規模堆芯瞬態輸運計算時，與單CPU相比加速倍數約在2～6倍，且加速比隨CMFD計算時間占比的增大而減小。本文僅初步實現了CMFD TFSP加速計算，所涉及的并行算法可推廣至預估-校正準靜態方法以及TML方法，提升全堆瞬態計算的效率。