復合Poisson -Geometric 風險模型下帶混合保費和投資的Gerber-Shiu 折現懲罰函數

覃利華

（廣西民族師范學院，數理與電子信息工程學院，廣西 崇左 532200）

在經典風險模型中，理賠過程為單一險種的風險經營過程，但隨著保險公司經營規模的不斷擴大以及新險種的不斷開發，用單一險種的風險模型來描述風險經營過程是有一定局限性的.因此對復合 Poisson 模型進行推廣，將單一險種推廣為雙險種.此外，經典風險模型假設保險公司在單位時間內收到的保費是某一固定常數，但是在實際的業務中，保險公司可能跟一些投保人簽訂協議，在每個單位時間內投保人都會定期交固定的保費，除此之外，保險公司在單位時間內還會收到不同保費的保單，這是服從某一分布的隨機變量.為了改進和優化經典風險模型，文獻[1-4]利用全期望公式和積分變換公式研究Poisson-Geometric風險模型的期望折現罰金函數.文獻[5]考慮了常利率下存在紅利界限和隨機干擾的風險模型.文獻[6]考慮了常數保費下雙險種索賠過程是Poisson-Geometric 過程的風險模型.文獻[7]考慮了確定風險投資和有界分紅的復合Poisson-Geometric 風險模型.文獻[8]討論借貸利率的影響，建立了帶有干擾的雙Poisson-Geometric的風險模型.文獻[9-10]均是在Poisson-Geometric 風險模型上做進一步推廣，保費到達和索賠到達均采用Poisson-Geometric 過程，建立相應的風險模型，給出保費和索賠均服從指數分布時破產概率的具體形式.

本文考慮隨機干擾因素的影響，建立了帶投資混合保費收取下的復合Poisson-Geometric 雙風險模型，該模型在固定保費收取的情況下，考慮保費的隨機化和險種的多元化，并且隨機保費到達過程服從復合Poisson 過程，理賠過程服從復合Poisson-Geometric 過程.

1 模型的建立及介紹

2 更新方程

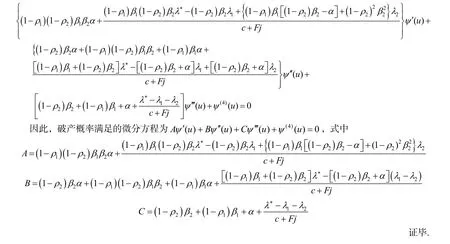
3 結語

本文考慮到保險公司經營過程中會受到不確定隨機干擾因素的影響，以及保費的隨機化和險種的多元化，建立混合保費收取下帶有隨機干擾因素和投資復合的Poisson-Geometric 雙風險模型，隨機保費到達過程服從復合Poisson 過程，理賠過程服從復合Poisson-Geometric 過程.推導了該模型Gerber-Shiu 折現罰金函數滿足的更新方程，進而得到破產時盈余懲罰期望，破產時刻赤字分布函數和破產概率滿足的更新方程，并當保費、理賠過程服從特定指數分布時，得到破產概率滿足的微分方程.