二值隨機變量與三值隨機變量的獨立性與相關性

◎郭俊娟 李國奎 （.昆明市第一中學西山學校，云南 昆明 65000；.昆明市西山區團結明朗中心學校，云南 昆明 650）

一、前 言

眾所周知，當兩個隨機變量相互獨立時，它們的相關系數為零（簡稱“不相關”）；反之，當它們不相關時，它們卻未必獨立.不相關且不獨立的隨機變量的例子已由諸多教科書與期刊文獻所舉出，茲不贅述.

一般來說，簡單的例子容易理解和驗證.因此，在構造“不相關且不獨立”的例子時，一種傾向便是在取值較少（因而較簡單）的離散型隨機變量中去尋找.這里值得注意的有如下結論：

（1）服從一點分布（或者說以概率1 等于常數）的隨機變量與任何隨機變量相互獨立.這種情況下，“不相關且不獨立”是談不上的.

（2）如果兩個隨機變量都服從兩點分布，那么當它們不相關時，它們一定相互獨立.此時“不相關且不獨立”也是不可能的.

（3）存在兩個隨機變量，一個服從兩點分布，另一個服從三點分布，它們不相關且不獨立.

這就是說，要找出“不相關且不獨立”的兩個離散型隨機變量的例子，對于隨機變量取值個數的最低要求是其中一個能取兩個值，而另一個能取三個值.為方便敘述，我們引入如下定義：

定義1.1設（X，Y）是一個二維離散型隨機變量.如果X的邊緣分布是兩點分布，而Y的邊緣分布是三點分布，那么稱（X，Y）為（2，3）點隨機變量.

本文在上述不相關且不獨立的（2，3）點隨機變量的例子基礎上，分類討論、詳細研究（2，3）點隨機變量相關性與獨立性的各種情況.

二、預備知識和引理

（一）隨機變量的不相關性

兩個隨機變量X與Y的相關系數規定為

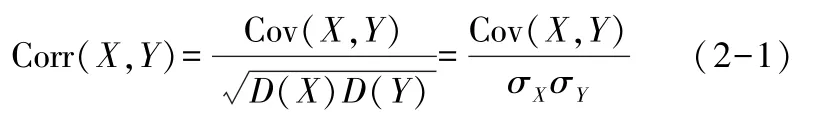
其中

（2－2）是X與Y的協方差，而D（X）＝Cov（X，X）為X的方差.

顯然X，Y不相關的充要條件便是Cov（X，Y）＝0.［嚴格說來，如果D（X）與D（Y）之一為零，譬如D（X）＝0，那么Corr（X，Y）是沒有定義的.但當D（X）＝0 時，X一定以概率1等于常數，這種情形我們是不予考慮的.］

此外，協方差還有如下性質：

（1）對稱性：Cov（X，Y）＝Cov（Y，X）；

（2）雙線性：Cov（aX1＋bX2，Y）＝aCov（X1，Y）＋bCov（X2，Y），a，b為常數；

（二）隨機變量的獨立性

我們只談取值個數有限的離散型隨機變量.那么，隨機變量X與Y相互獨立，其充分必要條件為對X的任意取值x和對Y的任意取值y，有

（2－3）式可以說成聯合分布等于邊緣分布的乘積.

為了給予獨立性一種更直觀的描述，設（X，Y）的聯合分布列如表2－1所示，其中pi，j＝P（X＝xi，Y＝yj），qi＝P（X＝xi），rj＝P（Y＝yj）.我們稱A＝（pi，j）為（X，Y）的聯合概率矩陣.

表2－1 典型有限值域二維離散型隨機變量聯合分布列

引理2.1有限值域的離散型隨機變量X與Y相互獨立，其充要條件是它們的概率矩陣A中，任意兩行（列）成比例，或者說A的秩為1.

如果X與Y相互獨立，那么依（2－3）顯然有

于是A的秩≤1.又由于A中所有元素之和為1，知A≠0，故A的秩恰為1.

反之，設A的秩為1，則由文獻知

qi＝bi／b，rj＝cj／c

由此（2－4）式成立，而且

（三）條件分布

為了在某些場合避免提及聯合分布，使敘述簡明，我們使用條件分布的概念.在表2－1中，所謂當Y＝yj時X的條件概率分布是指這樣一個列：其中

三、主要結果及例子

設（X，Y）是一個（2，3）點隨機變量，則按定義1.1，它的分布列具有表3－1的形式.其中，由于X服從兩點分布，為清晰起見我們不寫x0，x1而改寫作a，b；且p＝p0＋p1＋p2，q＝q0＋q1＋q2.這里，p，q，pi＋qi（i＝0，1，2）均不為零.

表3－1 一般（2，3）點隨機變量的聯合分布列

（一）主要結果

作為本文主要結果，我們將指出，X與Y的獨立性和不相關性，首先取決于（X，Y）的概率矩陣中，有多少個列與X的邊緣概率分布成比例，其次取決于yi（i＝0，1，2）的具體值.由于X的條件分布為

即當Y＝yi時，X的條件分布等于邊緣分布.

對此我們有如下定理：

定理3.1設（X，Y）是一個（2，3）點隨機變量，則

（ⅰ）如果Y至少有兩個取值，使得X的條件分布等于邊緣分布，則X與Y獨立；

（ⅱ）如果Y恰有一個取值，使得X的條件分布等于邊緣分布，則X與Y相關（因而必不獨立）；

（ⅲ）如果Y取任何值時X的條件分布都不等于邊緣分布，此時X與Y不獨立，但可通過適當調整Y的值域（即表3－1中的｛y0，y1，y2｝）而使得X與Y不相關.

（ⅰ）不妨設當Y＝y1和Y＝y2時X的條件分布等于邊緣分布，則有

因pi＋qi≠0，易見pi，qi均不為零.

這意味著（X，Y）的概率矩陣的兩行是成比例的，因而由引理2.1 知X，Y獨立.

（ⅱ）不妨設當Y＝y1時X的條件分布等于邊緣分布，而當Y＝y0和Y＝y2時則不如此.則我們有

現轉而考慮隨機變量X′＝X－a，Y′＝Y－y0.

由于協方差的雙線性，Cov（X′，Y′）＝Cov（X，Y）－Cov（a，Y）－Cov（X，y0）＋Cov（a，y0），

易見上式中涉及常數的一切項都為零，故Cov（X′，Y′）＝Cov（X，Y）.因此X′，Y′的相關性與X，Y的相關性等價.這樣一來，（X′，Y′）的聯合分布列如表3－2所示，其中

表3－2中，容易算得E（X′）＝b′q，E（Y′）＝y′1（p1＋q1）＋y′2（p2＋q2），E（X′Y′）＝b′y′1q1＋b′y′2q2.

表3－2 典型（2，3）點隨機變量的聯合分布列（簡化假設）

注意到p＋q＝1，我們有

顯然b′≠0（否則X′服從的就不是兩點分布了），因此Cov（X′，Y′）＝0 等價于y′1（pq1－qp1）＋y′2（pq2－qp2）＝0 （3－4）.

將（3－2）代入（3－4），得到y′2＝0，但這又與Y′服從三點分布不符.因此，在這種情況下Cov（X′，Y′）＝0 不能成立，X′與Y′（X與Y）一定相關.

（ⅲ）此時pqi－qpi（i＝0，1，2）均不為零.另一方面，假定X，Y獨立，則依獨立性準則（2－3）式應有

移項得pq1－qp1＝0，與題設矛盾，故X，Y不獨立.

為考察相關性，我們仍考慮隨機變量X′＝X－a和Y′＝Y－y0.易見，只要取y′1＝k（qp2－pq2），y′2＝k（pq1－qp1）（3－5）.

其中，k為任意非零常數就能使得（3－4）式成立.依題設，y′1和y′2均不為零，且y′1－y′2＝k（pq0－qp0）≠0.

因此，0，y′1，y′2是三個互不相同的值，且當Y′取這些值時，在表3－2中有Cov（X′，Y′）＝0.于是，在（3－5）式的基礎上，任取y0并通過（3－3）式來規定y1，y2，則y0，y1，y2是三個互不相同的值，且當Y取這些值時，在表3－1中有Cov（X，Y）＝0，即X，Y不相關.

（二）一些例子

我們通過具體例子來對定理3.1 加以說明，見表3－3、表3－4與表3－5.這里，由于定理3.1 的結論與Y的邊緣分布以及X的具體取值無關，我們略去了Y的邊緣分布一行，并設X的兩個值為0 和1.

表3－3 情形（ⅰ）：X，Y 獨立

表3－4 情形（ⅱ）：X，Y 相關，且相關性不能消除

表3－5 情形（ⅲ）：X，Y 不獨立，但適當規定yi 的值可使其不相關

在表3－3中，概率矩陣的三個列顯然成比例，故X，Y獨立.獨立與否是概率矩陣本身蘊含的性質，與X，Y的具體取值無關.

因此若要X，Y不相關，除非y2＝y0，而這是不可能的.

在表3－5中，概率矩陣的所有列都不與X的邊緣分布成比例.這時X，Y不獨立，但

因此只要取y1＝1，y2＝－1，y0＝0，就能使得Cov（X，Y）＝0，即X，Y不相關.

四、結 語

在絕大多數情況下，隨機變量的獨立性是比不相關性強得多的條件.實際上，設（X，Y）是一個二維離散型隨機變量，X能取n個值而Y能取m個值，則X與Y的獨立性意味著（n－1）（m－1）個方程［因為這時（X，Y）的概率矩陣中，其余（n－1）個行必須與某特定行成比例，而為了兩行成比例又需要（m－ 1）個方程］，而X與Y的不相關性，即Cov（X，Y）＝0，僅僅是一個方程而已.只有在n＝m＝2 的情形下，不相關性才能與獨立性等價.

本文所討論的是n＝2，m＝3 的情形.在定理3.1 為這種情形劃分的三種子情形中，（ⅰ）和（ⅱ）都與n＝m＝2 的情形緊密關聯.事實上，對于（ⅰ）無須多言；對于（ⅱ），如果Y＝yi時X的條件分布等于邊緣分布，那么條件隨機變量為二值隨機變量，這時我們便回到了n＝m＝2 的情形：X與不獨立，它們必定相關，而由于

Cov（X，Y）＝Cov（X，）·P（Y≠yi），

X與Y也必定相關.于是，只有子情形（ⅲ）才是新的，它構成尋找“不相關且不獨立”的（2，3）點隨機變量的理論基礎.

當然，我們還可進一步考慮n＝2，m＝k（k＞3）的情形，但從這里的討論可以預見，這些情形與n＝2，m＝3 的情形并無本質區別，只是細節上更復雜而已.