如何幫助學生練就“數學的眼光”

○王文英

“會用數學的眼光觀察現實世界，會用數學的思維思考現實世界，會用數學的語言表達現實世界”是《義務教育數學課程標準（2022年版）》（以下簡稱《課標（2022年版）》）的課程目標。如何將“三會”素養落地是數學教學研究的主要內容，本文擬就培養“數學的眼光”談談自己的思考與實踐。

一、如何理解“數學的眼光”

什么是“數學的眼光”？《課標（2022年版）》指出：數學為人們提供了一種認識與探究現實世界的觀察方式。簡而言之，“數學的眼光”就是數學的觀察方式。觀察是有目的、有計劃的知覺活動，是以視覺為主，包含著積極的思維活動，融其他感覺為一體的綜合感知。史寧中教授認為，學過數學的人看世界會抽象，會一般地看問題，數學的眼光最主要表現為抽象。

抽象是從許多事物中舍棄個別的、非本質屬性，得到共同的、本質屬性的思維過程，是形成概念的必要手段。《課標（2022年版）》指出，數學中的抽象主要是指對現實世界中數量關系與空間形式的抽象，通過抽象得到數學的研究對象，形成數學概念、性質、法則和方法。因此，練就“數學的眼光”應著力培養學生的數學抽象能力。

數學抽象主要包括兩個方面：數量與數量關系、圖形與圖形關系。這就意味著，數學抽象不僅僅要抽象出數學所要研究的對象，還要抽象出這些研究對象之間的關系。數學抽象可以理解為過程，即如何將數學的研究對象從現實世界的情境中層層剝離，抽象出數學的研究對象及其關系的過程。如通過觀察斜拉橋的鋼索、人字梁、自行車三腳架，忽略其顏色、材料質地等，將其外形畫下，則都是三角形。再進一步觀察，發現都是三角形但大小不同，其大小與底和高的長短有關。這一系列的過程是抽象。

數學抽象還可以理解為結果，即如何用形式化的語言表征數學對象及事物之間簡單的聯系與規律。如天平保持平衡，通過觀察，用3x=150 這個數學的式子表示相等關系，這也是抽象。

數學教學的過程應該是幫助學生不斷進行數學抽象的過程，在抽象的過程中，讓學生認識所學的數學知識，了解知識間的聯系，發現事物之間的規律，并且養成從數學的角度觀察現實世界的意識和習慣。如果學生擁有這樣的意識和能力，那就具有“數學的眼光”。

二、如何練就“數學的眼光”

1.培養數學觀察的意識。

讓學生養成從數學角度觀察現實世界的意識與習慣，是練就“數學的眼光”的關鍵。

第一，讓學生明確“觀察什么”。數學觀察不同于語文、美術等學科，主要聚焦的是數量和數量關系、圖形和圖形關系。從一年級起，教師要有意識地加以引導。比如一年級上冊教材，一開始就安排了“數一數”“比一比”“分一分”“認位置”四個內容。通過教學，不僅要讓學生學會怎么數、怎么比、怎么分、怎么描述位置，更重要的是讓學生知道，“數”“比”“分”以及“位置”都是數學研究的內容，可以從“數量有多少”“數量之間有什么關系”“怎樣確定標準去分類”“如何描述物體的位置”這些角度去觀察現實世界的客觀現象，這些角度既是數學觀察的角度，得到的也是數學的信息。同時，隨著年級的升高，需讓學生掌握數學觀察的其他角度，了解哪些信息是屬于數學的信息。

第二，讓學生知道“怎么觀察”。如何觀察，包含兩個方面。一是從哪里著眼。一般來說，是先整體后局部。無論是主題圖還是現實情境，整體觀察，初步了解其中包含的數學信息，然后局部觀察，具體觀察相應的對象。二是觀察時做什么。觀察不僅僅是看，還需要想，需要寫。要讓學生養成邊觀察邊思考、邊觀察邊記錄的習慣，及時將看到的與已學的知識聯系起來，將看到的與想到的記錄下來。

如這道題（圖1）：涂色部分的面積比空白部分的面積大16平方厘米，空白部分的面積是多少？

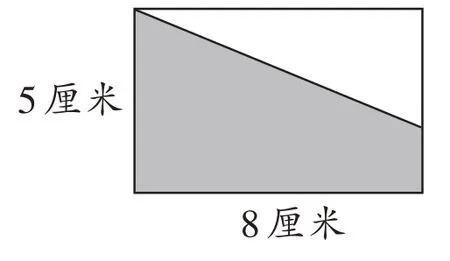
圖1

從常規角度思考，要求空白部分面積需將長方形面積減去涂色部分的梯形面積，顯然，這里的梯形面積很難求出。然而，一個學生在觀察時，將題意用線段圖表示出來（圖2），就將問題化為相對簡單的和差問題，用（40-16）÷2 就使問題得以解決。

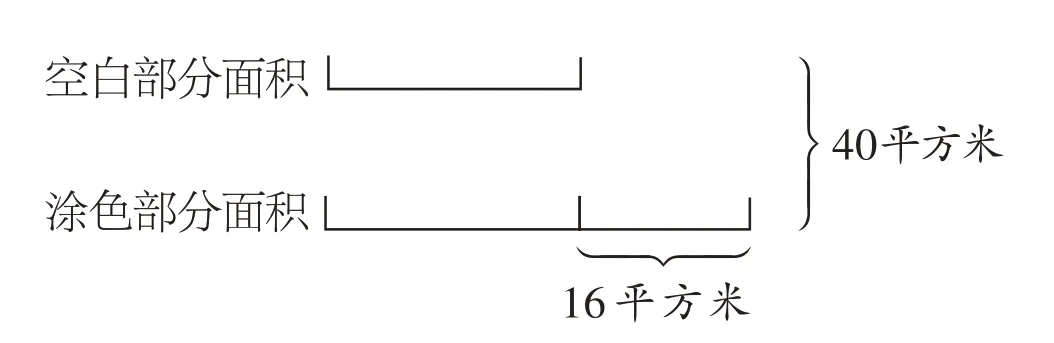
圖2

第三，需要不斷促使學生觀察進階。從一開始觀察數量的多少到關注數量之間的關系，從知道圖形是什么到清楚圖形之間的關系，教師需要根據學生對知識掌握的情況對觀察的視角與內容作更高的要求。如在認識乘法后，要求學生從“幾個幾”的角度去觀察并描述；在認識數級后，引導學生看到大數目就會自動分級，分析億級、萬級和個級上的數分別是多少。從模糊的整體到清晰的局部，再到相對精準的整體，說明學生觀察的視角和能力在不斷進階。

2.教會數學抽象的方法。

會觀察是前提，將觀察的結果用形式化的方式表示出來，就實現了數學抽象，這是練就“數學的眼光”的重要體現。

第一，引導比較。抽象需要引導學生抽取事物的本質特征，舍棄其非本質特征。需要教師有意識地引導學生對不同事物進行比較。如教學《認識圓柱體》，教師可以出示生活中的一些圓柱形的物體，如茶葉罐、蚊香盒、鉛筆等，引導學生觀察并思考：這些物體的形狀是什么？它們都是不同的物體，為何都稱之為圓柱？這些問題驅使學生發現不同圓柱物體的本質特征，即“上下一樣粗”“上下是圓形，大小相等，中間是個曲面”。當學生發現其相同點之后，教師繼續追問：“它們都是圓柱體，有不同之處嗎？”學生不難發現，同是圓柱，但因高矮、胖瘦不同，其大小不同。透過現象看到本質，這是抽象的關鍵一步，顯然，通過比較能夠達成。

第二，適當表征。當學生成功抽取事物的本質屬性之后，教師要鼓勵學生用形式化的方式將之表示出來。如上例，教師可以這樣小結并提問：“盡管這些圓柱粗細、高矮各不相同，但它們有本質的相同之處，能否嘗試畫出一個圓柱表示它們的相同之處呢？”史寧中教授認為，幾何抽象的本質就是把三維的物體用二維圖形表現出來。讓學生將自己觀察發現的結果在紙上畫出來，畫的過程實際就是將圓柱形物體抽象成圓柱形的過程。

第三，賦予意義。當抽取出圓柱形之后，教師還需要帶著學生向前一步，即給出不同大小的圓柱形，讓學生想象可能表示生活中的哪個物體。根據圖形想物體，這一逆向的觀察思考對培養學生的空間觀念非常有益。教學中，很多教師容易忽略這一環節，往往表征后被認為完成了抽象，殊不知，當抽象之后賦予其現實意義，這樣的抽象才更完整。

3.創造應用數學的機會。

數學與生活是密切聯系的，引導學生在日常生活及其他學科中發現并研究數學問題，是練就“數學的眼光”的重要途徑。

可以把生活情境引入數學課堂。首先，將生活情境引入課堂發現數學問題。如一位教師創設了這樣的情境：茫茫大海上，一艘輪船出了事故，需要緊急救援。作為搜救艇艇長，了解哪些信息后才能施救？學生不難發現，艇長必須準確地了解輪船的位置，即“在什么方向，距離多少”。其次，將生活情境引入課堂幫助理解數學知識。“半個月前，媽媽買了一箱蘋果共20 個，第一個星期全家人吃了6 個，第二個星期全家人吃了8 個，現在還剩多少個？”用這個生活實例幫助學生理解減法的性質。再次，還可用生活情境檢驗學生知識掌握的情況。如教學《認識圓》后，教師設計問題：媽媽準備過年全家聚餐，是選擇用條形桌、八仙桌還是圓桌？請說明理由。以此來檢驗學生對圓的特征的掌握程度。

以主題學習探究現實世界。在教學中，教師可以通過組織主題學習，給學生提供應用數學知識探究現實世界的機會。如將常見樹葉的形狀、周長、面積，以及包含的“比”等知識作為學習內容，讓學生體會數學學習的價值，探究樹葉這一常見事物蘊含的數學信息，激發對現實世界的好奇心和對數學學習的求知欲。

三、練就“數學的眼光”幾個注意點

1.“三會”素養是一個整體。

“數學的眼光”“數學的思維”“數學的語言”作為“三會”的具體內容，《課標（2022年版）》對它們分別作了闡述，并有具體要求。作為教師，需要明確的是，它們是一個整體，盡管在培養過程中有所側重，但非獨立存在。如《認識乘法分配律》的教學，教師設計了三個環節：第一，引導學生觀察不同情境：鼓樂隊添服裝、兩輛車從兩地相對駛出相遇求路程、兩塊長方形地求總面積。學生發現求解三個問題都可以用兩種方法解決，一種是先相加再相乘，另一種是分別乘再相加。第二，在此基礎上引導學生猜想、驗證，發現規律，并用含有字母的式子表示，即（a+b）c=ac+bc。第三，應用規律解決實際問題。在這個過程中，“三會”的培養都有具體落實。

2.培養“數學的眼光”有階段性。

在課堂教學中，培養“數學的眼光”并非一蹴而就，需要日積月累，逐步遞進。如《用字母表示數》，教材安排在五年級教學，但這并不意味著五年級才開始培養學生的符號意識。符號意識的培養從一年級起就應該滲透。比如，白兔和黑兔一共有15 只，其中白兔有8 只，黑兔有多少只？可以鼓勵學生用□表示黑兔，用8+□=15 來表示這道題。隨著□表示未知數→用字母表示未知數→字母不僅表示未知數，還可以表示變化的數，學生逐漸使用符號→體會字母表示數的意義→自覺地用字母表示數。因此，同樣是符號意識的培養，不同學段應該有不同的要求。